改进的北方苍鹰算法优化BP神经网络---回归+分类两种案例
今天采用前作者自行改进的一个算法---融合正余弦和折射反向学习的北方苍鹰(SCNGO)优化算法优化BP神经网络。
文章一次性讲解两种案例,回归与分类。回归案例中,作者选用了一个经典的股票数据。分类案例中,选用的是公用的UCI数据集。
BP神经网络初始的权值阈值都是随机生成的,因此不一定是最佳的。采用智能算法优化BP神经网络的权值阈值,使得输入与输出有更加完美的映射关系,以此来提升BP神经网络模型的精度。本文采用SCNGO算法对BP神经网络的权值阈值进行优化,并应用于实际的回归和分类案例中。
01 股票预测案例
案例虽然介绍的是股票预测,但是SCNGO-BP预测模型是通用的,大家根据自己的数据直接替换即可。
股票数据特征有:开盘价,盘中最高价,盘中最低价,收盘价等。预测值为股票价格。股票数据整理代码已写好,想换成自己数据的童鞋不需要理解此代码,替换数据即可。下面直接上标准BP的预测结果和SCNGO-BP的预测结果。
标准BP模型预测结果:
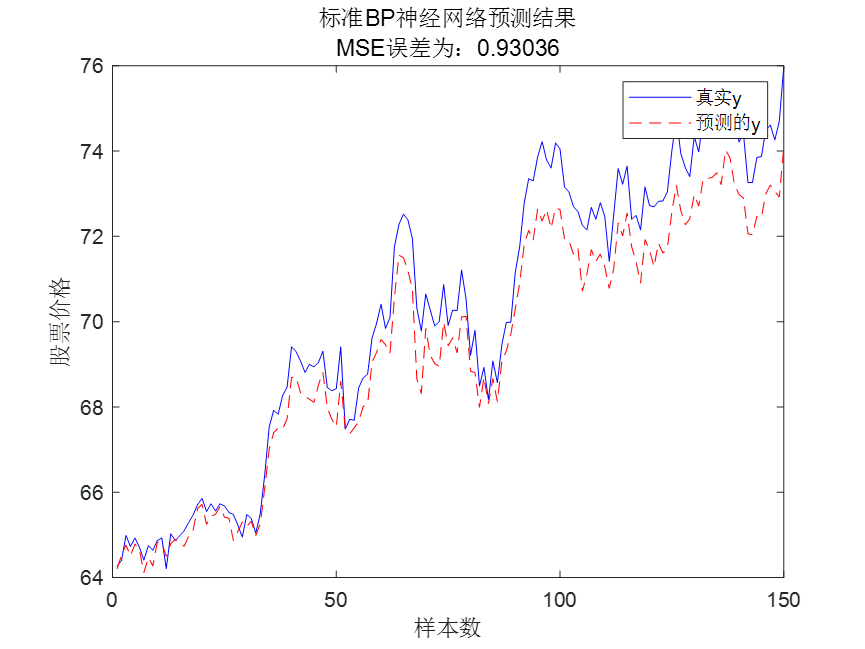
可以看到标准BP神经网络的预测效果不是很理想,无法跟踪真实值,偏差较大。
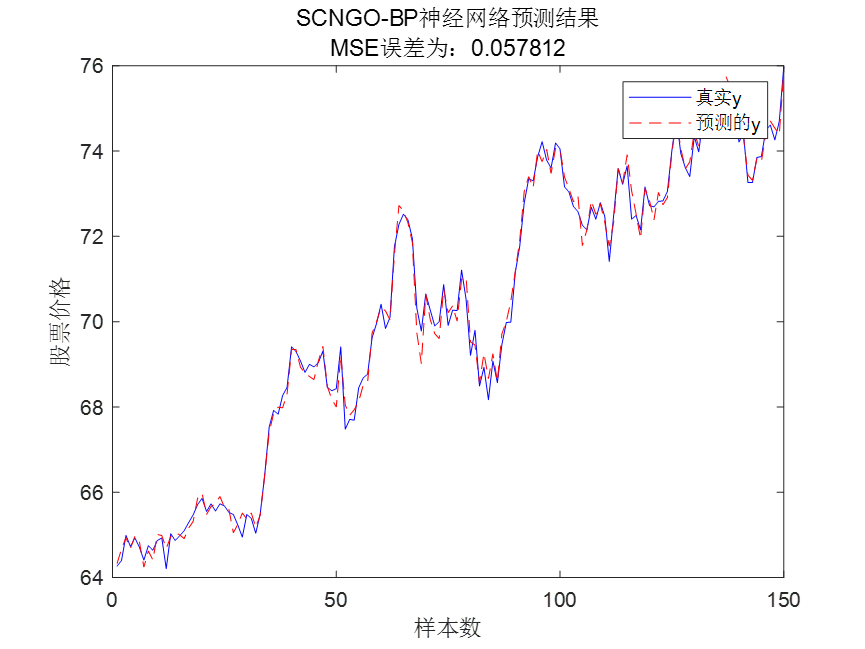
SCNGO-BP预测结果:
可以看到SCNGO-BP神经网络的预测值可以紧密跟随真实值,效果很好。
将真实值,BP预测值和SCNGO-BP预测值放在一起,效果更加明显。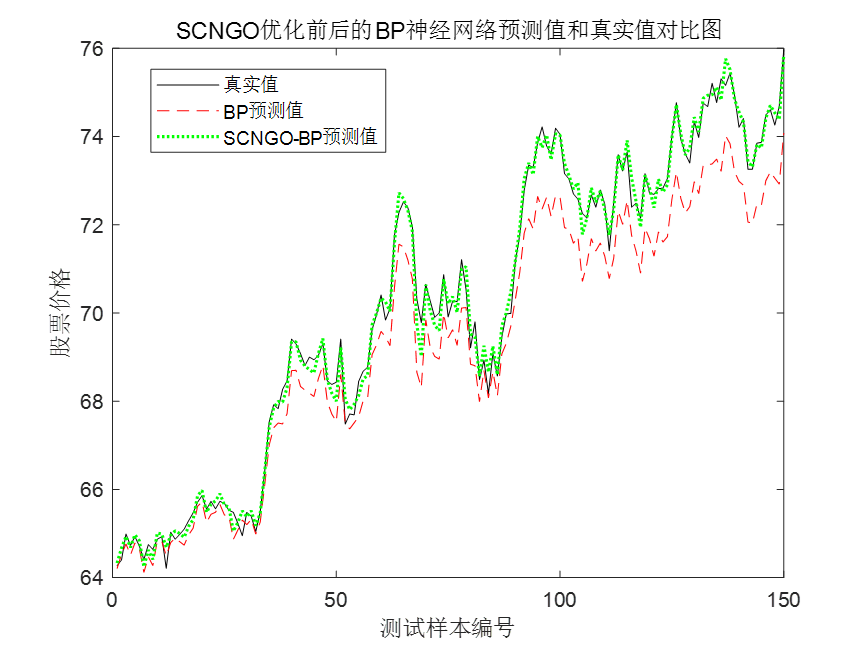
接下来是一个SCNGO优化前后的BP神经网络误差对比图。
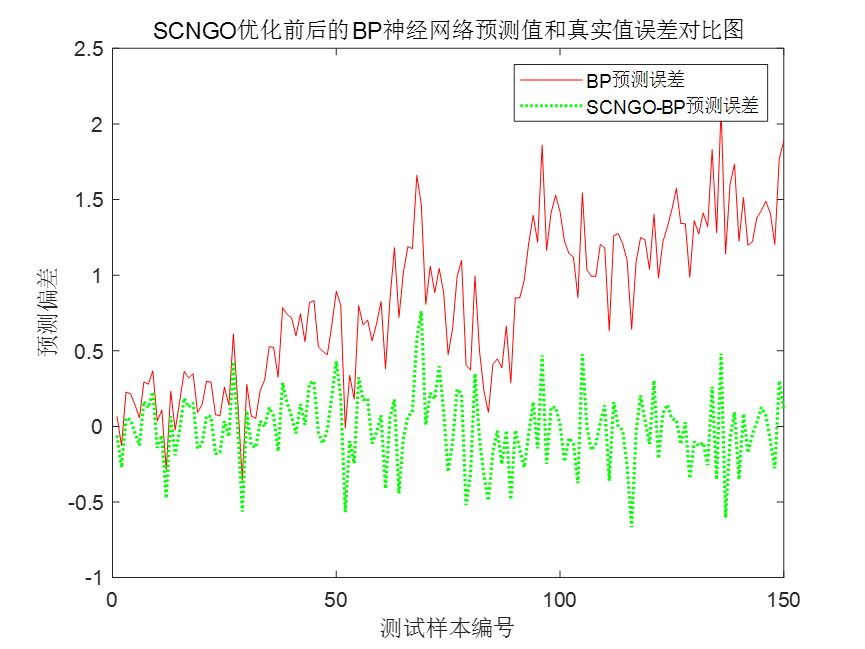
SCNGO-BP的迭代曲线,以预测值和真实值的MSE为目标函数。
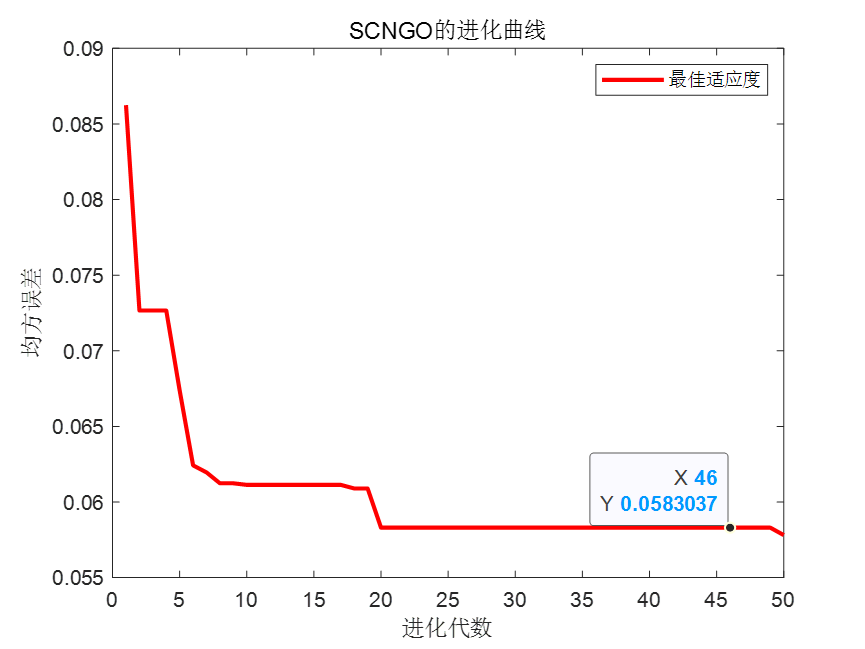
SCNGO-BP预测模型的评价:可以看到,SCNGO-BP方法在股票预测案例中可以很好地进行股票价格预测。
02 分类案例
接下来是SCNGO-BP的分类案例,采用的数据是UCI数据集中的Balancescale.mat数据,该数据一共分为三类。接下来看结果。
标准BP模型分类结果:
混淆矩阵结果图:
简单说一下这个图该怎么理解。请大家横着看,每行的数据加起来是100%,每行的数据个数加起来就是测试集中第一类数据的真实个数。以第一行为例,测试集中一共有12个数据是属于第一类的,而12个数据中,有8个预测正确,有1个预测成了第2类,3个预测成了第三类。其他行均这样理解。
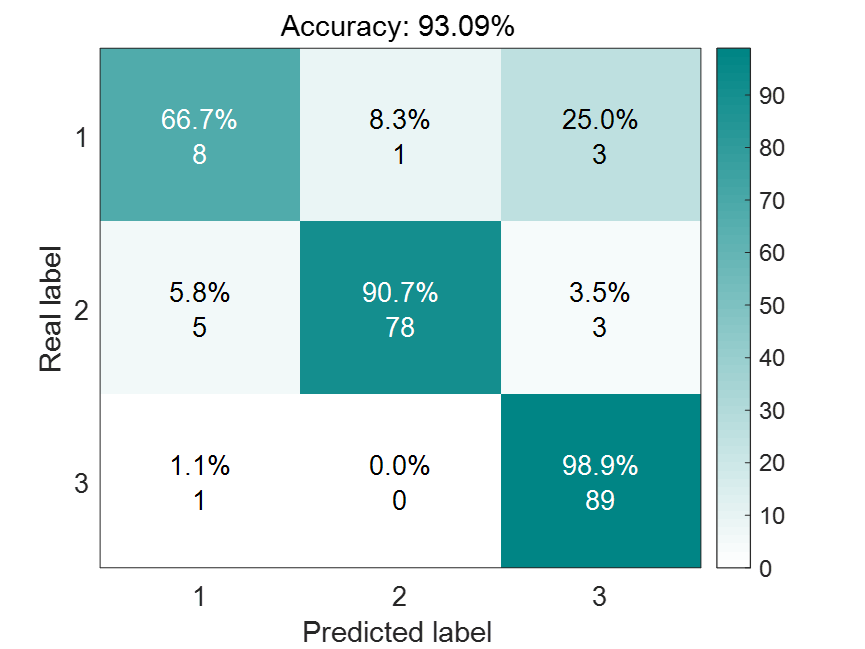
下面这个图是另一种结果展现方式,在一些论文中会用这种方式展示结果。
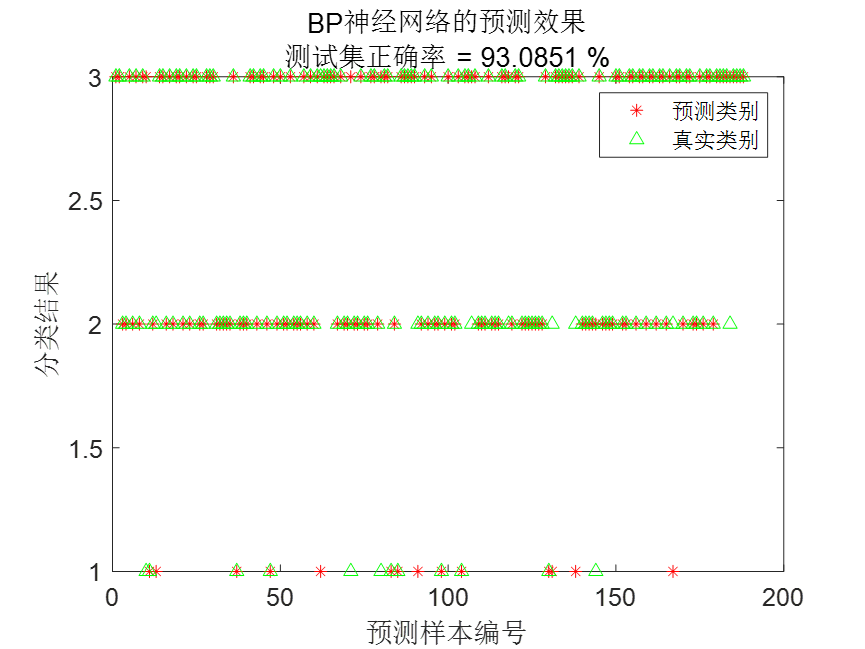
SCNGO-BP分类结果:
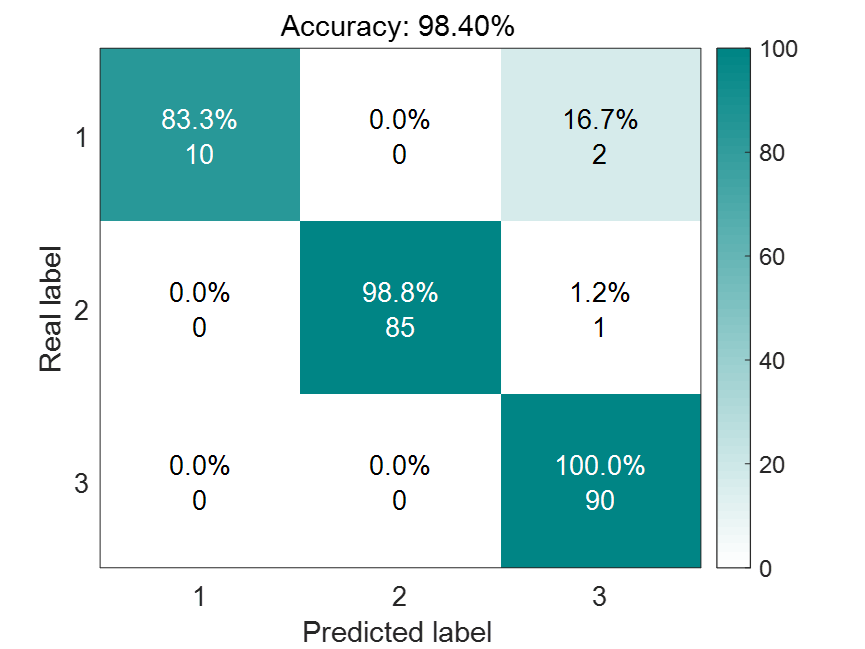
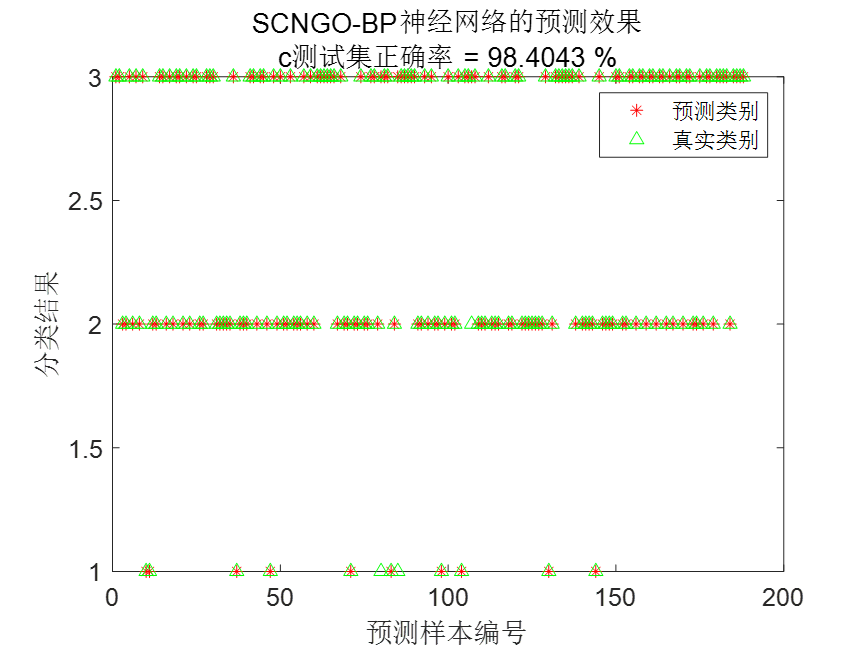
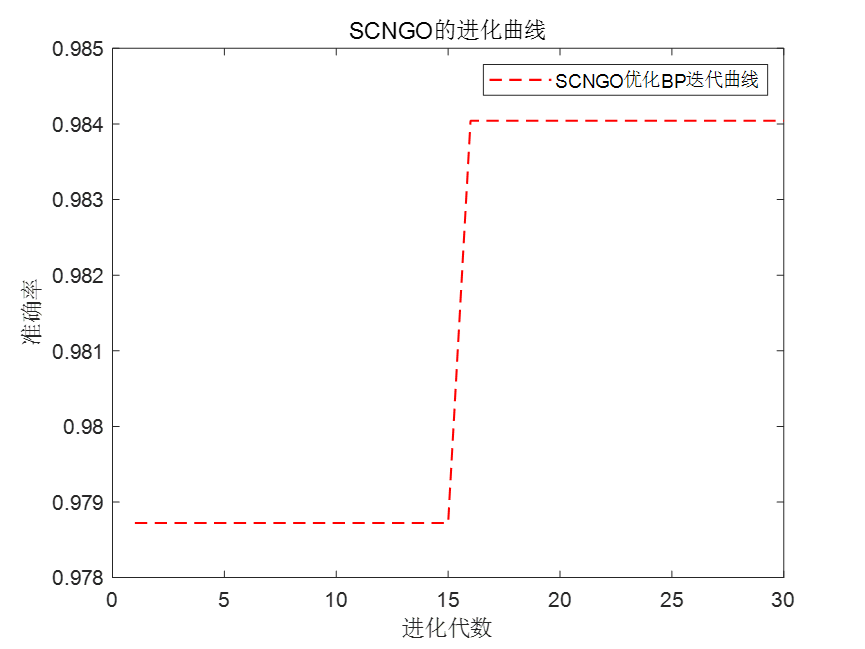
03 代码展示
%% 初始化
clear
close all
clc
warning off
addpath(genpath(pwd));
% rng(0)
load Balancescale.mat
data = Balancescale;
data=data(randperm(size(data,1)),:); %此行代码用于打乱原始样本,使训练集测试集随机被抽取,有助于更新预测结果。
input=data(:,2:end);
output1 =data(:,1);
for i=1:size(data,1)switch output1(i)case 1output(i,1)=1;case 2output(i,2)=1;case 3output(i,3)=1;case 4output(i,4)=1;case 5output(i,5)=1;case 6output(i,6)=1;case 7output(i,7)=1;end
end
%% 划分训练集和测试集
m=fix(size(data,1)*0.7); %训练的样本数目
%训练集
input_train=input(1:m,:)';
output_train=output(1:m,:)';
% 测试集
input_test=input(m+1:end,:)';
output_test=output(m+1:end,:)';%% 数据归一化
[inputn,inputps]=mapminmax(input_train,0,1);
inputn_test=mapminmax('apply',input_test,inputps);
dam = fix(size(inputn,2)*0.3);%选30%的训练集作为验证集
idx = randperm(size(inputn,2),dam);
XValidation = inputn(:,idx);
inputn(:,idx) = [];
YValidation = output_train(:,idx);
output_train(:,idx) = [];%% 获取输入层节点、输出层节点个数
inputnum=size(input_train,1);
outputnum=size(output_train,1);
disp('/')
disp('神经网络结构...')
disp(['输入层的节点数为:',num2str(inputnum)])
disp(['输出层的节点数为:',num2str(outputnum)])
disp(' ')
disp('隐含层节点的确定过程...')%确定隐含层节点个数
%采用经验公式hiddennum=sqrt(m+n)+a,m为输入层节点个数,n为输出层节点个数,a一般取为1-10之间的整数
acc = 0;
for hiddennum=fix(sqrt(inputnum+outputnum))+1:fix(sqrt(inputnum+outputnum))+10net0=newff(inputn,output_train,hiddennum);% 网络参数net0.trainParam.epochs=1000; % 训练次数,这里设置为1000次net0.trainParam.lr=0.01; % 学习速率,这里设置为0.01net0.trainParam.goal=0.0001; % 训练目标最小误差,这里设置为0.0001net0.trainParam.show=25; % 显示频率,这里设置为每训练25次显示一次net0.trainParam.mc=0.001; % 动量因子net0.trainParam.min_grad=1e-8; % 最小性能梯度net0.trainParam.max_fail=6; % 最高失败次数net0.trainParam.showWindow = false;net0.trainParam.showCommandLine = false; % 网络训练[net0,tr]=train(net0,inputn,output_train);an0=sim(net0,XValidation); %验证集的仿真结果predict_label=zeros(1,size(an0,2));for i=1:size(an0,2)predict_label(i)=find(an0(:,i)==max(an0(:,i)));endoutputt=zeros(1,size(YValidation,2));for i=1:size(YValidation,2)outputt(i)=find(YValidation(:,i)==max(YValidation(:,i)));endaccuracy=sum(outputt==predict_label)/length(outputt); %计算预测的确率disp(['隐含层节点数为',num2str(hiddennum),'时,验证集的准确率为:',num2str(accuracy)])%更新最佳的隐含层节点if acc<accuracyacc=accuracy;hiddennum_best=hiddennum;end
end
disp(['最佳的隐含层节点数为:',num2str(hiddennum_best),',验证集相应的训练集的准确率为:',num2str(acc)])%% 构建最佳隐含层节点的BP神经网络
disp(' ')
disp('标准的BP神经网络:')
net0=newff(inputn,output_train,hiddennum_best,{'tansig','purelin'},'trainlm');% 建立模型
%网络参数配置
net0.trainParam.epochs=1000; % 训练次数,这里设置为1000次
net0.trainParam.lr=0.01; % 学习速率,这里设置为0.01
net0.trainParam.goal=0.00001; % 训练目标最小误差,这里设置为0.0001
net0.trainParam.show=25; % 显示频率,这里设置为每训练25次显示一次
net0.trainParam.mc=0.01; % 动量因子
net0.trainParam.min_grad=1e-6; % 最小性能梯度
net0.trainParam.max_fail=6; % 最高失败次数
% net0.trainParam.showWindow = false;
% net0.trainParam.showCommandLine = false; %隐藏仿真界面
%开始训练
net0=train(net0,inputn,output_train);%预测
an0=sim(net0,inputn_test); %用训练好的模型进行仿真
predict_label=zeros(1,size(an0,2));for i=1:size(an0,2)predict_label(i)=find(an0(:,i)==max(an0(:,i)));endoutputt=zeros(1,size(output_test,2));for i=1:size(output_test,2)outputt(i)=find(output_test(:,i)==max(output_test(:,i)));endaccuracy=sum(outputt==predict_label)/length(outputt); %计算预测的确率 disp(['准确率为:',num2str(accuracy)])
%% 标准BP神经网络作图
% 画方框图
figure
confMat = confusionmat(outputt,predict_label); %output_test是真实值标签
zjyanseplotConfMat(confMat.');
xlabel('Predicted label')
ylabel('Real label')
% 作图
figure
scatter(1:length(predict_label),predict_label,'r*')
hold on
scatter(1:length(predict_label),outputt,'g^')
legend('预测类别','真实类别','NorthWest')
title({'BP神经网络的预测效果',['测试集正确率 = ',num2str(accuracy*100),' %']})
xlabel('预测样本编号')
ylabel('分类结果')
box on
set(gca,'fontsize',12)代码中注释非常详细,有对神经网络构建的注释,有对SCNGO-BP代码的注释,简单易懂。
代码附带UCI常用的数据集及其解释。大家可以自行尝试别的数据进行分类。附带SCNGO在CEC2005函数的测试代码。
完整代码获取方式,后台回复关键词。关键词 :
SCNGOBP
相关文章:

改进的北方苍鹰算法优化BP神经网络---回归+分类两种案例
今天采用前作者自行改进的一个算法---融合正余弦和折射反向学习的北方苍鹰(SCNGO)优化算法优化BP神经网络。 文章一次性讲解两种案例,回归与分类。回归案例中,作者选用了一个经典的股票数据。分类案例中,选用的是公用的UCI数据集。 BP神经网络…...

等保工作如何和企业创新业务发展相结合,实现“安全”和“创新”的火花碰撞?
等保工作如何和企业创新业务发展相结合,实现“安全”和“创新”的火花碰撞?在当今数字化浪潮的背景下,企业越来越需要在“安全”和“创新”之间找到平衡点,以实现业务的持续创新和安全的有效保障。等保工作可以为企业提供安全保障…...

23.7.25 杭电暑期多校3部分题解
1005 - Out of Control 题目大意 解题思路 code 1009 - Operation Hope 题意、思路待补 code #include <bits/stdc.h> using namespace std; const int N 1e5 9; struct lol {int x, id;} e[3][N * 2]; int t, n, a[3][N * 2], hd[3], tl[3], vis[N * 2], q[N * …...

【设计模式——学习笔记】23种设计模式——桥接模式Bridge(原理讲解+应用场景介绍+案例介绍+Java代码实现)
问题引入 现在对不同手机类型的不同品牌实现操作编程(比如:开机、关机、上网,打电话等),如图 【对应类图】 【分析】 扩展性问题(类爆炸),如果我们再增加手机的样式(旋转式),就需要增加各个品牌手机的类,同样如果我们…...
文档翻译软件那么多,哪个能满足你的多语言需求?
想象一下,你手中拿着一份外文文件,上面记录着珍贵的知识和信息,但是语言的障碍让你无法领略其中的内容。而此时,一位翻译大师闪亮登场!他的翻译技巧犹如一把魔法笔,能够将文字的魅力和意境完美传递。无论是…...

MySQL 中NULL和空值的区别
MySQL 中NULL和空值的区别? 简介NULL也就是在字段中存储NULL值,空值也就是字段中存储空字符(’’)。区别 1、空值不占空间,NULL值占空间。当字段不为NULL时,也可以插入空值。 2、当使用 IS NOT NULL 或者 IS NULL 时࿰…...
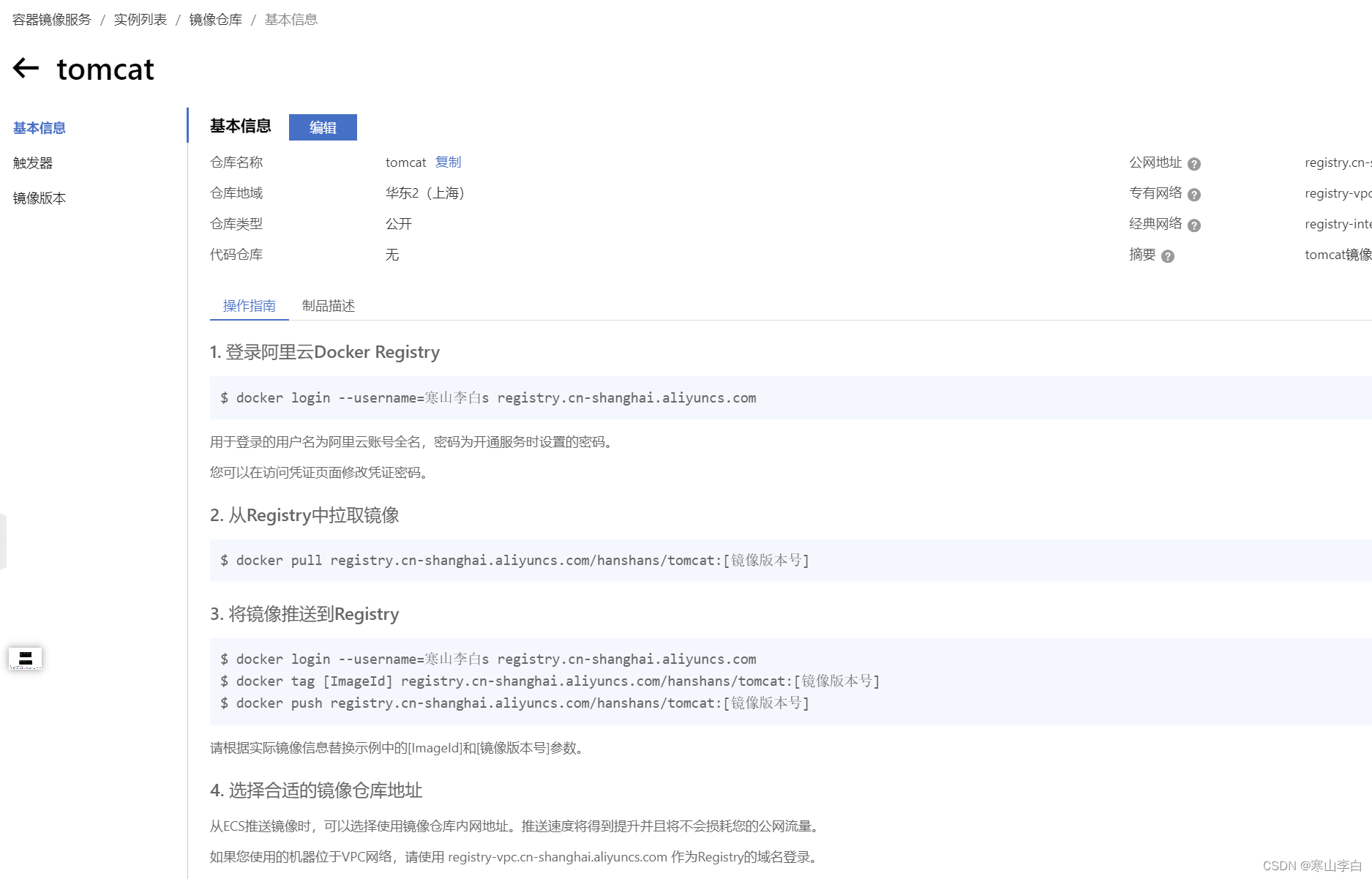
阿里云容器镜像仓库(ACR)的创建和使用
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

工业的相机与镜头(简单选型)
面阵相机,需要多大的分辨率?多少帧数? 前提条件: 1.被检测的物体大小 2.要求检测的精度是多少 3.物体是否在运动过程中进行检测,速度是多少 线阵相机选择(分辨率、扫描行数) 行频:每秒扫描多少行…...
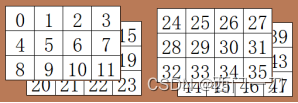
numpy广播机制介绍
广播 广播机制的意义:广播描述了在算术运算期间NumPy如何处理具有不同形状的数组。受某些约束条件的限制,较小的数组会在较大的数组中“广播”,以便它们具有兼容的形状。 在对两个数组进行操作时,NumPy按元素对它们的形状进行比…...

RocketMQ 5.0 无状态实时性消费详解
作者:绍舒 背景 RocketMQ 5.0 版本引入了 Proxy 模块、无状态 pop 消费机制和 gRPC 协议等创新功能,同时还推出了一种全新的客户端类型:SimpleConsumer。 SimpleConsumer 客户端采用了无状态的 pop 机制,彻底解决了在客户端发布…...
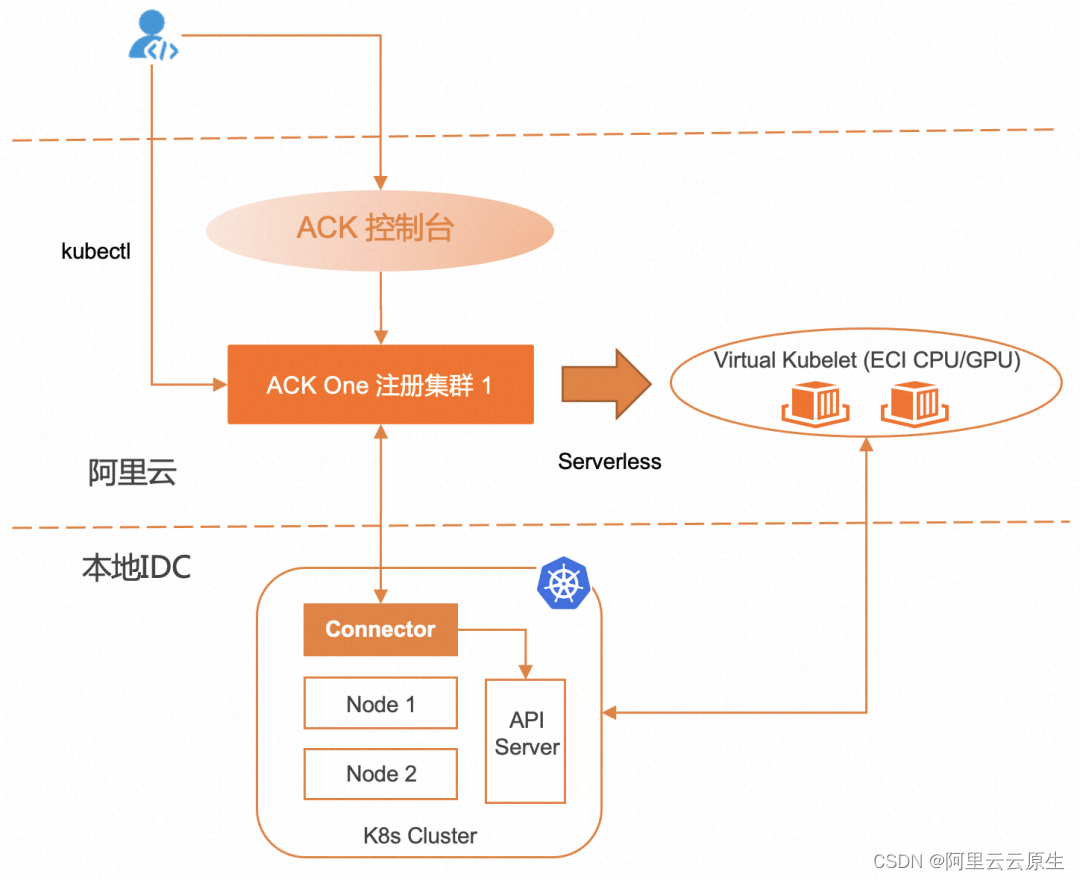
本地 IDC 中的 K8s 集群如何以 Serverless 方式使用云上计算资源
作者:庄宇 在前一篇文章《应对突发流量,如何快速为自建 K8s 添加云上弹性能力》中,我们介绍了如何为 IDC 中 K8s 集群添加云上节点,应对业务流量的增长,通过多级弹性调度,灵活使用云上资源,并通…...
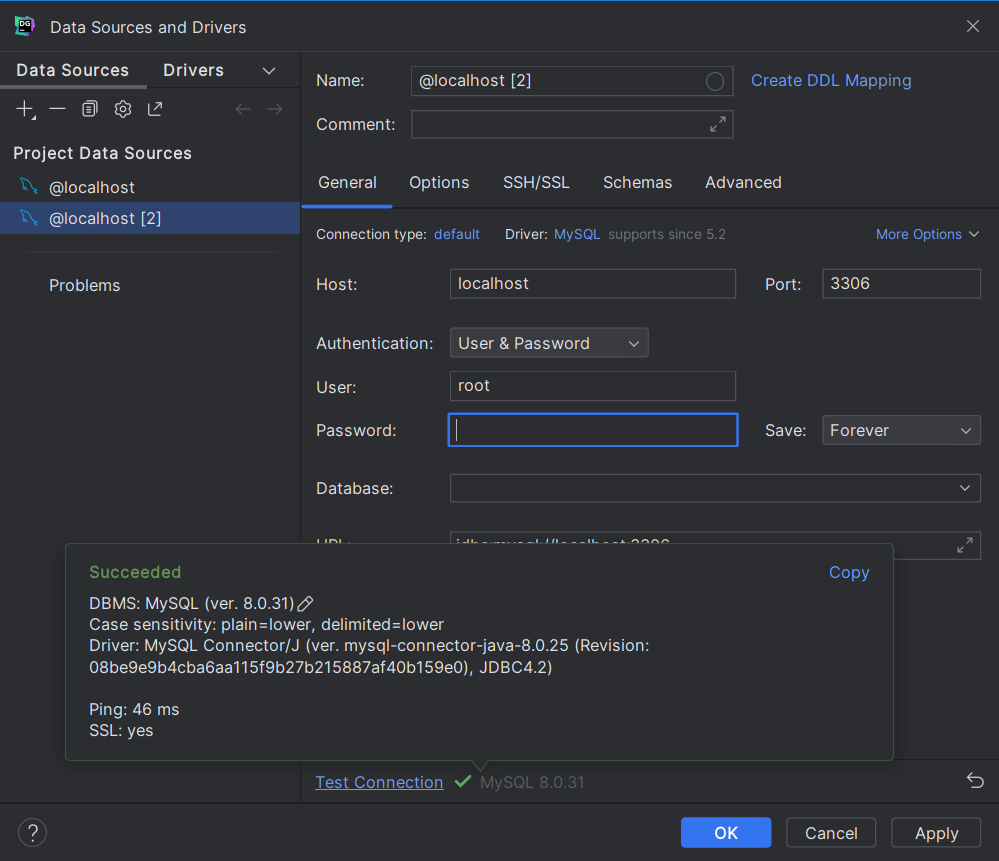
MySQL - 安装、连接、简单介绍
1、安装 MySQL8.0 安装MySQL 8.0的步骤,以 Windows 为例: 1.1 下载MySQL Installer: 需要从MySQL官方网站下载MySQL Installer。在下载页面中,选择适用于Windows的MySQL Installer并下载。 1.2 运行MySQL Installer࿱…...
)
【算法】求欧拉函数(包括完整的证明以及代码模板,建议收藏)
求欧拉函数 前置知识 互质:互质是公约数只有1的两个整数,叫做互质整数。 欧拉函数定义 1 ∼ N − 1 1∼N-1 1∼N−1中与N互质的数的个数被称为欧拉函数,记为 ϕ ( N ) \phi(N) ϕ(N)。 若在算数基本定理中, N p 1 a 1 p 2 a 2 .…...
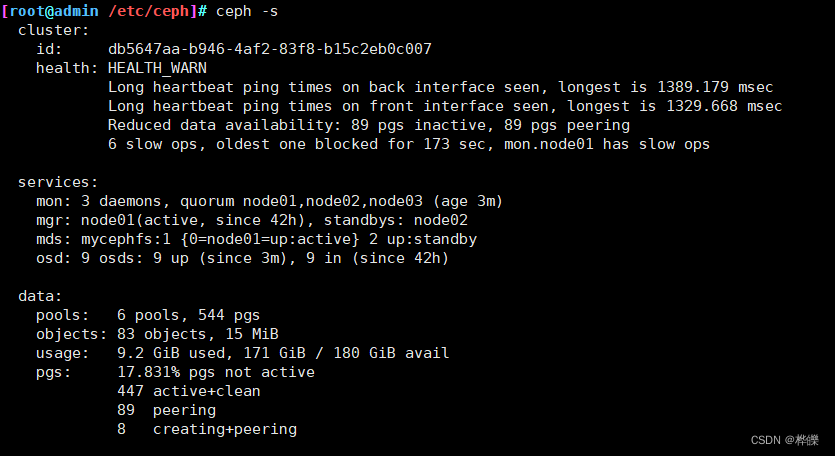
Ceph的应用
文章目录 一、创建 CephFS 文件系统 MDS 接口1)在管理节点创建 mds 服务2)查看各个节点的 mds 服务3)创建存储池,启用 ceph 文件系统4)查看mds状态,一个up,其余两个待命,目前的工作的…...
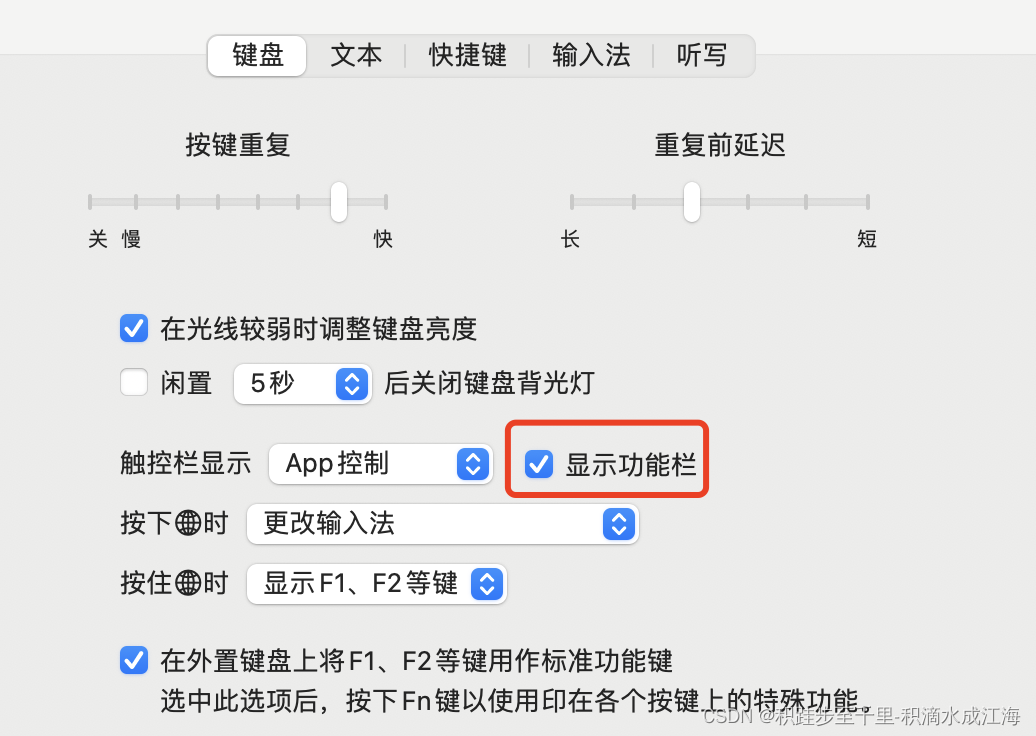
mac m1 触控栏TouchBar功能栏异常
电脑可能在高温下运行时间过长,导致TouchBar之前正常显示的调整屏幕亮度与调整声音等功能的按钮均丢失,然后看了一眼键盘设置,设置也是正常的,已勾选显示功能栏 下面请看 如何在MacBook Pro(macOS Monterey࿰…...

“奢侈品”价格的“快消品”,竹叶青这么想赚年轻人的“茶水钱”?
文 | 螳螂观察 作者 | 青月 或许是受养生焦虑的影响,这届年轻人似乎爱上了喝茶。 《抖音电商茶行业洞察报告》数据显示, 年轻客群已经成为了抖音电商茶行业的增长极,在茶叶、茶具、茶文化书籍等方面,18-30岁消费者是当之无愧消…...
)
【Matlab】基于随机森林算法的时间序列预测(Excel可直接替换数据)
【Matlab】基于随机森林算法的时间序列预测(Excel可直接替换数据) 1.模型原理2.数学公式3.文件结构4.Excel数据5.分块代码6.完整代码7.运行结果1.模型原理 基于随机森林算法的时间序列预测是一种利用随机森林模型来解决时间序列预测问题的方法。在传统的随机森林算法中,对于…...
vue 中断请求
1 背景:针对一些请求时间较长,组件销毁后即中断请求; 2 方法: data(){return {//用于取消请求abortController:new AbortController(), } }, created(){//请求接口this.groundAcquisition(); }, beforeDestroy(){//中断请求this.…...

Jwt(Json web token)——从Http协议到session+cookie到Token Jwt介绍 Jwt的应用:登陆验证的流程
目录 引出从Http协议到session&cookie到TokenHTTP协议session & cookiesessioncookie为什么需要session & cookie? JavaEE传统解决长连接方案问题:分布式不适用解决方案:令牌Token Jwt,Json web tokenjwt的结构Header加密算法Ba…...
Java使用 java.util.regex.Pattern 正则表达式校验参数值是否规范
场景: java中我们可以利用 Pattern 注解对某个入参进行规则校验,但有些特殊参数在接口入口处不方便校验,需要在代码中校验 一、使用 Pattern 注解校验 Pattern(regexp "^[a-zA-Z0-9]$", message "xxx号限输入字母、…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

【题解-洛谷】P10480 可达性统计
题目:P10480 可达性统计 题目描述 给定一张 N N N 个点 M M M 条边的有向无环图,分别统计从每个点出发能够到达的点的数量。 输入格式 第一行两个整数 N , M N,M N,M,接下来 M M M 行每行两个整数 x , y x,y x,y,表示从 …...
