2023牛客暑期多校第二场部分题解
索引
- A
- B
- C
- D
- E
- F
- G
- H
- I
- K
A
队友开的题,说是其实就是问能不能用若干个数异或出来某个数。
应该就是线性基板子,然后他写了一下就过了。
B
一开始看没什么人过不是很敢开,结果到后面一看题——这不是最大权闭合子图板子吗??
我还愣了一小会儿,只是发现边数有点儿多,要用个树剖+线段树优化建图,然后就开始咣咣一顿写,极限40min写完……然后没debug出来。
后来发现一个变量ID 写成了Id。再也不起这么抽象的变量名了。
代码如下:
#include <bits/stdc++.h>
using namespace std;
#define maxn 100010
#define inf 999999999999999999ll//开大了,忘记改了,问题不大int n,m,N;
struct edge{int y,next;long long z;
}e[20000000];
int first[maxn],et=1;
void buildroad(int x,int y,long long z){e[++et]=(edge){y,first[x],z};first[x]=et;
}
void addedge(int x,int y,long long z){// printf(" %d->%d : %lld\n",x,y,z);buildroad(x,y,z);buildroad(y,x,0);
}
vector<pair<int,int>> to[maxn];
int fa[maxn],Fa[maxn],dep[maxn];
int sz[maxn],mson[maxn];
void dfs_init(int x){sz[x]=1;for(auto i:to[x]){int y=i.first;if(y==fa[x])continue;fa[y]=x;Fa[y]=i.second;dep[y]=dep[x]+1;dfs_init(y);sz[x]+=sz[y];if(sz[y]>sz[mson[x]])mson[x]=y;}
}
int top[maxn],bot[maxn],id[maxn],old[maxn],Id=0;
struct node{int l,r,mid,ID;node *zuo,*you;node(int x,int y,int L):l(x),r(y),mid(l+r>>1){ID=++N;if(l==r){if(L<l)addedge(ID,Fa[old[l]]+m,inf);//就是这个ID写错了……return;}zuo=new node(l,mid,L);you=new node(mid+1,r,L);addedge(ID,zuo->ID,inf);addedge(ID,you->ID,inf);}void link(int x,int y,int From){if(l==x&&r==y){addedge(From,Id,inf);return;}if(y<=mid)zuo->link(x,y,From);else if(x>mid)you->link(x,y,From);else zuo->link(x,mid,From),you->link(mid+1,y,From);}
}*rt[maxn];
void dfs2(int x,int tp){id[x]=++Id;old[Id]=x;top[x]=tp;if(mson[x]){dfs2(mson[x],tp);for(auto i:to[x]){int y=i.first;if(y==fa[x]||y==mson[x])continue;dfs2(y,y);}}else bot[tp]=x;if(x==tp)rt[x]=new node(id[x],id[bot[x]],id[x]);
}
int S,T;
int q[maxn],st,ed,h[maxn],cur[maxn];
bool bfs(){memset(h,0,sizeof(h));q[st=ed=1]=S;h[S]=1;while(st<=ed){int x=q[st++];cur[x]=first[x];for(int i=first[x];i;i=e[i].next){int y=e[i].y;if(e[i].z&&!h[y]){h[y]=h[x]+1;q[++ed]=y;}}}return h[T]>0;
}
long long dfs(int x,long long flow){if(x==T)return flow;long long re=0;for(int i=cur[x];i;i=e[i].next){int y=e[i].y;cur[x]=i;if(e[i].z&&h[y]==h[x]+1){long long p=dfs(y,min(e[i].z,flow));re+=p;e[i].z-=p;e[i^1].z+=p;if(re==flow)break;}}if(!re)h[x]=0;return re;
}
void go(int x,int y,int From){if(dep[top[x]]>dep[top[y]])swap(x,y);while(top[x]!=top[y]){rt[top[y]]->link(id[top[y]],id[y],From);addedge(From,Fa[top[y]]+m,inf);y=fa[top[y]];if(dep[top[x]]>dep[top[y]])swap(x,y);}if(id[x]>id[y])swap(x,y);rt[top[x]]->link(id[x],id[y],From);
}int main()
{scanf("%d %d",&n,&m);S=n+m;T=S+1;N=T+1;for(int i=1;i<n;i++){int x,y,z;scanf("%d %d %d",&x,&y,&z);to[x].push_back(make_pair(y,i));to[y].push_back(make_pair(x,i));addedge(i+m,T,z);}dfs_init(1);dfs2(1,1);long long ans=0;for(int i=1;i<=m;i++){int x,y,z1,z2;scanf("%d %d %d %d",&x,&y,&z1,&z2);if(z1-z2>0){ans+=z1-z2;addedge(S,i,z1-z2);go(x,y,i);}}while(bfs())ans-=dfs(S,inf);printf("%lld",ans);
}
C
把欧拉路径先限制成欧拉回路,虽然看起来更难了但其实这样不需要考虑图的实际连通情况了,只需要保证每个点的度都是偶数。
那么很容易想到把图里的奇数点先拎出来,构造完剩余的图之后再把这个点尝试加进去。但实际上剩余的图构造完之后这个点怎么加都会破坏和他相连的点的度的奇偶性。
官方题解的方法就很妙,把奇度点 x x x 拎出来之后,让与他相连的点集 P P P 构成的子图取一个补图,然后再让剩下的图去做构造,然后看看 P P P 内染 0 0 0 和 1 1 1 的点分别有多少,数量必然是一奇一偶,将 x x x 加入偶数的那个集合即可,手算一下此时的度就能发现都变成偶数了。
代码如下:
#include <bits/stdc++.h>
using namespace std;
#define maxn 110int n,m;
int d[maxn][maxn],r[maxn];
int ans[maxn];
bool v[maxn];
int fa[maxn];
int findfa(int x){return x==fa[x]?x:fa[x]=findfa(fa[x]);}
vector<int> s[maxn];
void work(vector<int> &a){for(int i:a)if(!v[i]&&r[i]){v[i]=true;vector<int> tmp;for(int j:a)if(d[i][j])tmp.push_back(j),d[i][j]^=1,d[j][i]^=1,r[i]^=1,r[j]^=1;for(int x:tmp)for(int y:tmp)if(x!=y)d[x][y]^=1,r[x]^=1;work(a);int zero=0,one=0;for(int j:tmp)if(ans[j])one++;else zero++;if(zero&1)ans[i]=1;v[i]=false;break;}
}int main()
{scanf("%d %d",&n,&m);for(int i=1;i<=n;i++)fa[i]=i;for(int i=1;i<=m;i++){int x,y;scanf("%d %d",&x,&y);d[x][y]^=1;d[y][x]^=1;r[x]^=1;r[y]^=1;fa[findfa(y)]=findfa(x);}for(int i=1;i<=n;i++)s[findfa(i)].push_back(i);for(int i=1;i<=n;i++)if(i==fa[i])work(s[i]);for(int i=1;i<=n;i++)printf("%d ",ans[i]);
}
D
首先可以发现每个人的决策一定会想办法利用后面的人来使自己利益最大化,那么利用肯定利用到极致,比如最后选菜的人最喜欢的菜一定是没人选的,因为这样他就一定会选这个菜,前面的人就可以利用这一点。
所以实际上最后相当于反向贪心一下就行了。
代码是队友写的,就不贴了,也没啥实现难度。
E
要求 y 2 = x × 1 0 k + c y^2=x\times 10^k+c y2=x×10k+c 即 y = x × 1 0 k + c y=\sqrt{x\times 10^k +c} y=x×10k+c,注意到 c c c 其实影响很小,所以 y = ⌈ x × 1 0 k ⌉ y=\lceil \sqrt{x\times 10^k}\rceil y=⌈x×10k⌉。
枚举 k k k 尝试求解即可。
代码如下:
#include <bits/stdc++.h>
using namespace std;int main()
{cin.sync_with_stdio(false);int T;cin>>T;while(T--){long long n;cin>>n;int ans=0;long long c=1;for(int k=0;;k++){int p=sqrt(n)+1e-6;if(1ll*p*p/c==n/c)ans=p;p++;if(1ll*p*p/c==n/c)ans=p;if(ans)break;if(n>(long long)(1e17+0.5))break;n*=10;c*=10;}if(!ans)cout<<"-1\n";else cout<<ans<<'\n';}
}
F
注意到其实是个很经典的二分图模型。二分图博弈的结论是:假如起点无论如何都在最大匹配内,那么先手必胜。证明可以上网找,其实在最大匹配内就是要保证每次后手操作后先手一定可以操作。
把这个结论往这题上套,发现 n n n 是偶数时一定每个点都在最大匹配上,先手一定必胜, n n n 是奇数时二分图两侧点数是不一样的, x + y + z x+y+z x+y+z 为奇数的点多一个,并且一定可以通过构造让任何一个 x + y + z x+y+z x+y+z 为奇数的点不在最大匹配内,所以此时先手必败。如果 x + y + z x+y+z x+y+z 为偶数那么还是先手必胜。
代码很简单就不贴了。
G
魔改一个马拉车即可。
最后贪心找子串来拼接,正确性可以这样考虑:
假设有一个串(方便看和理解这里使用传统意义的回文串) a b a c a b a abacaba abacaba,那么贪心选可能会选出 a b a c a b a \red{aba} c \red{aba} abacaba 这三段来覆盖,但如果存在更长一点的回文串可以覆盖这一段为什么不选呢?比如这里可以直接选整段,但这就意味着,前面的 a b a \red{aba} aba 在后面一定会对应另一个 a b a \red{aba} aba,所以不考虑这个长段也无所谓。
代码是队友写的,就不贴了。
H
一开始想着对每种二进制数的长度分别在操作序列上建线段树来找下一个变成 0 0 0 的位置,然后每次一个一个位置往后跳,应该是可以做的,但实现很麻烦。
后来想到直接不管长度限制,统一直接用一个 unsigned long long 来做,加一就正常加一,翻转后的加一变成减一,翻转就用 2 63 − 1 2^{63}-1 263−1 来减去当前的数,最后需要多少位就截取多少位直接输出即可。注意到这样子不需要考虑进位溢出的情况了,所以把所有操作做一个前缀和每次就可以 O ( 64 ) O(64) O(64) 回答了。
又是之前提到的先不考虑限制直接做,然后求出在限制下的答案的思想,非常经典。
代码如下:
#include <bits/stdc++.h>
using namespace std;
#define maxn 200010int n,m;
char s[maxn],ss[110];
int b[maxn],sum[maxn];int main()
{scanf("%d %d",&n,&m);scanf("%s",s+1);int now=1;for(int i=1;i<=n;i++){if(s[i]=='A')now*=-1,sum[i]=sum[i-1];else sum[i]=sum[i-1]+now;b[i]=now;}long long lastans=0;vector<int> ans;for(int i=1;i<=m;i++){int l,r,L,R,len;scanf("%d %d %s",&L,&R,ss+1);l=min((lastans^L)%n+1,(lastans^R)%n+1);r=max((lastans^L)%n+1,(lastans^R)%n+1);// printf("real : %d %d\n",l,r);len=strlen(ss+1);unsigned long long num=0;for(int j=1;j<=len;j++)num=(num<<1)+ss[j]-'0';int bl=s[l]=='A'?b[l]*(-1):b[l];num+=bl*(sum[r]-sum[l-1]);if(bl!=b[r])num=ULONG_LONG_MAX-num;lastans=0;for(int j=1;j<=len;j++)ans.push_back(num&1),num>>=1;while(ans.size()){lastans=(lastans<<1)+ans.back();putchar(ans.back()+'0'),ans.pop_back();}puts("");// printf("lastans : %lld\n\n",lastans);}
}
I
样例其实已经提示了构造方法了,就是每行(或每列)四个四个放,假如 n , m n,m n,m 都是奇数那么特殊考虑一下最后一列和最后一行即可,具体可以看代码:
#include <bits/stdc++.h>
using namespace std;int main()
{int T;scanf("%d",&T);while(T--){int n,m;scanf("%d %d",&n,&m);if(n%2==0){for(int i=1;i<=n;i++){for(int j=1;j<=m;j++)putchar((i+(j-1)/4)%2?'x':'o');puts("");}}else if(m%2==0){for(int i=1;i<=n;i++){for(int j=1;j<=m;j++)putchar((j+(i-1)/4)%2?'x':'o');puts("");}}else{int d=(n+(m-2)/4)%2;for(int i=1;i<n;i++){for(int j=1;j<m;j++){putchar((i+(j-1)/4+d)%2?'x':'o');}putchar((i+(m-2)/4+d)%2?'o':'x');puts("");}for(int i=1;i<=m;i++)putchar((n+(m-2)/4-i+1+d)%2?'o':'x');puts("");}}
}
K
状态很少,dp一下即可,考虑每一个cover放在左中右哪个盒子上,注意不能和上一个cover交错放,要不然可能放在了上上个帽子上。
代码如下:
#include <bits/stdc++.h>
using namespace std;
#define maxn 1000010int n,m,a[maxn],pos[maxn];
long long f[maxn][3];int main()
{scanf("%d",&n);for(int i=1;i<=n;i++)scanf("%d",&a[i]);for(int i=1;i<=n;i++){int x;scanf("%d",&x);if(x)pos[++m]=i;}if(!m){printf("0");return 0;}for(int i=0;i<3;i++)f[1][i]=a[pos[1]+i-1];for(int i=2;i<=m;i++){for(int j=0;j<3;j++)for(int k=0;k<3;k++)if(pos[i]+k-1>pos[i-1]+j-1)f[i][k]=max(f[i][k],f[i-1][j]+a[pos[i]+k-1]);}long long ans=max(f[m][0],max(f[m][1],f[m][2]));printf("%lld",ans);
}
相关文章:

2023牛客暑期多校第二场部分题解
索引 ABCDEFGHIK A 队友开的题,说是其实就是问能不能用若干个数异或出来某个数。 应该就是线性基板子,然后他写了一下就过了。 B 一开始看没什么人过不是很敢开,结果到后面一看题——这不是最大权闭合子图板子吗??…...
20230724将真我Realme手机GT NEO3连接到WIN10的电脑的步骤
20230724将真我Realme手机GT NEO3连接到WIN10的电脑的步骤 2023/7/24 23:23 缘起:因为找使用IMX766的手机,找到Realme手机GT NEO3了。 同样使用IMX766的还有:Redmi Note12Pro 5G IMX766 旗舰影像 OIS光学防抖 OLED柔性直屏 8GB256GB时光蓝 现…...
黑马 pink h5+css3+移动端前端
网页概念 网页是网站的一页,网页有很多元素组成,包括视频图片文字视频链接等等,以.htm和.html后缀结尾,俗称html文件 HTML 超文本标记语言,描述网页语言,不是编程语言,是标记语言,有标签组成 超文本指的是不光文本,还有图片视频等等标签 常用浏览器 firefox google safari…...

Docker的七项优秀实践
众所周知,作为一个文本文档,Dockerfile包含了用户创建镜像的所有命令和说明。Docker可以通过读取Dockerfile中指令的方式,去自动构建镜像。因此,大家往往认为编写Dockerfile理应非常简单,只需从互联网上选择一个示例&a…...

【数据结构】24王道考研笔记——图
六、图 目录 六、图定义及基本术语图的定义有向图以及无向图简单图以及多重图度顶点-顶点间关系连通图、强连通图子图连通分量强连通分量生成树生成森林边的权、带权网/图特殊形态的图 图的存储及基本操作邻接矩阵邻接表法十字链表邻接多重表分析对比图的基本操作 图的遍历广度…...
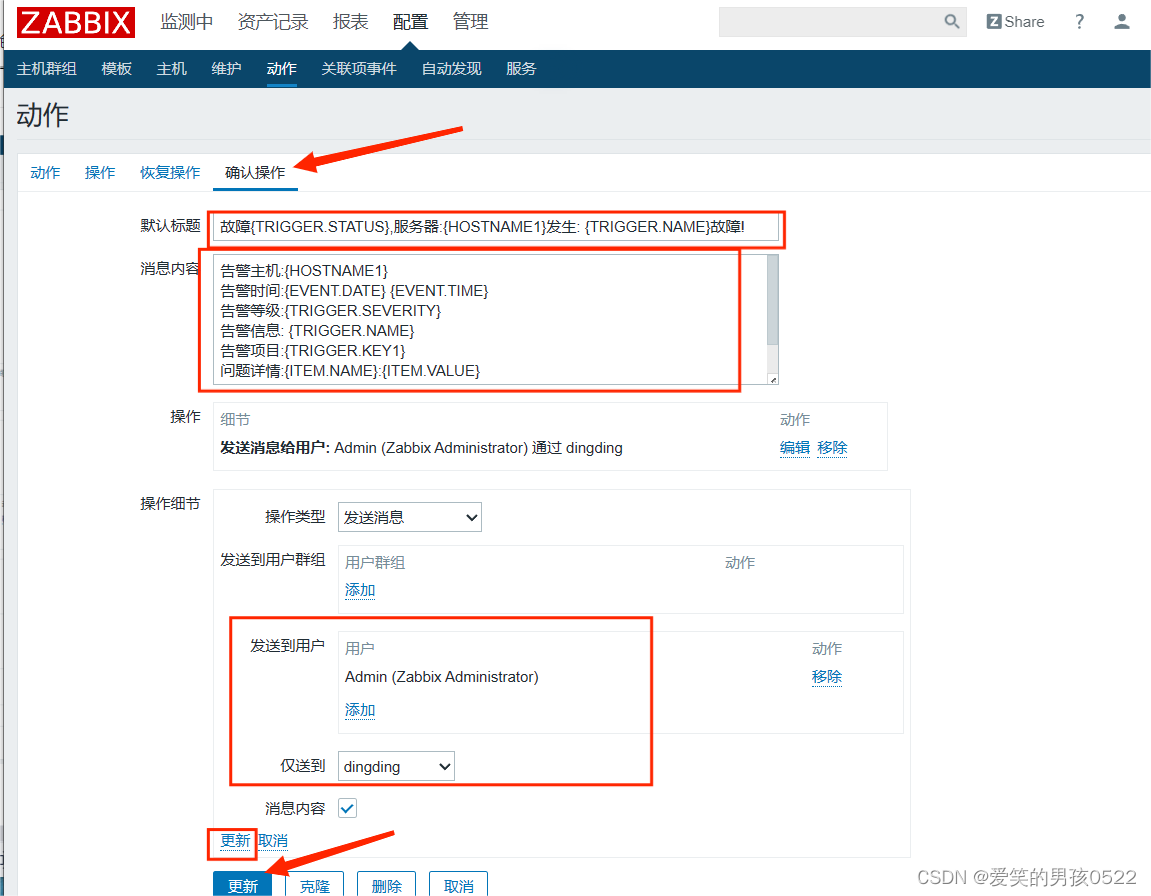
zabbix钉钉报警
登录钉钉客户端,创建一个群,把需要收到报警信息的人员都拉到这个群内. 然后点击群右上角 的"群机器人"->"添加机器人"->"自定义", 记录该机器人的webhook值。 添加机器人 在钉钉群中,找到只能群助手 添加机器人 选择自定义机…...
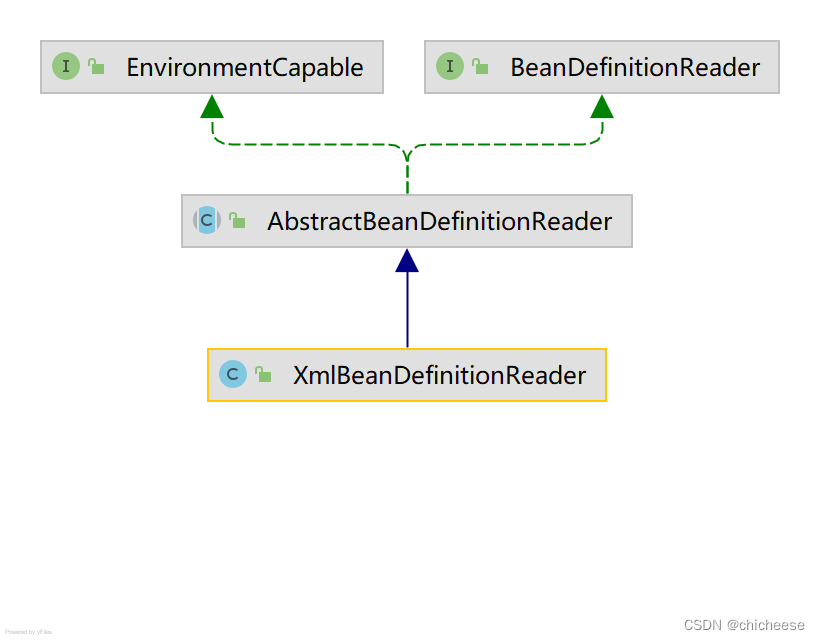
Spring 源码解读
1、Spring 的结构组成 1.1、核心类介绍 Spring 中有两个最核心的类 1 DefaultListableBeanFactory XmlBeanFactory 继承自 DefaultListableBeanFactory,而DefaultListableBeanFactory 是整个 bean加载的核心部分,是 Spring 注册及加载 bean 的默认实现…...
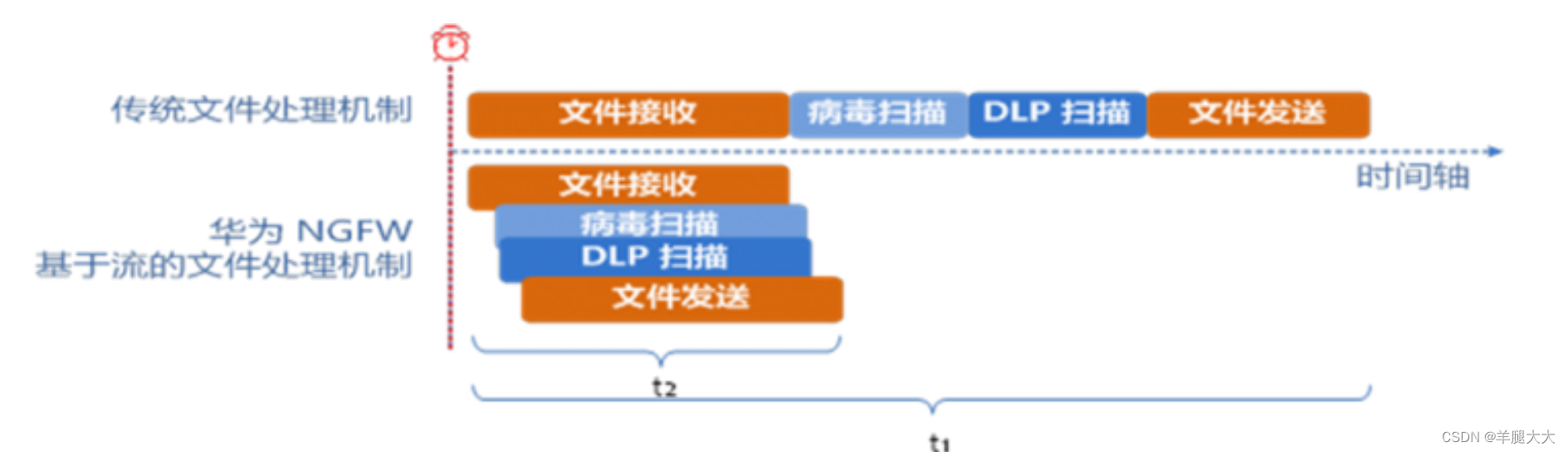
练习时长两年半的网络安全防御“first”
1.网络安全常识及术语 下边基于这次攻击演示我们介绍一下网络安全的一些常识和术语。 资产 任何对组织业务具有价值的信息资产,包括计算机硬件、通信设施、 IT 环境、数据库、软件、文档资料、信息服务和人员等。 网络安全 网络安全是指网络系统的硬件、软件及…...

HttpRunner自动化测试之响应中文乱码处理
响应中文乱码: 当调用接口,响应正文返回的中文是乱码时,一般是响应正文的编码格式不为 utf-8 导致,此时需要根据实际的编码格式处理 示例: 图1中 extract 提取title标题,output 输出 title 变量值&#x…...
idea使用命令将jar包导入到maven仓库中
因为今天突然忘了命令,记下来方便以后查看 pom文件的依赖 jar包路径 进入idea中命令窗 输入命令 mvn install:install-file -DfileD:\Project\spring-cloud\dubbo-api\target\dubbo-api-1.0-SNAPSHOT.jar -DgroupIdcom.wmx -DartifactIddubbo-api -Dversion1.0…...
 Standalone模式(单机模式)安装)
zookeeper学习(一) Standalone模式(单机模式)安装
安装准备 centos7环境jdk1.8环境zookeeper安装包 安装jdk 上传jdk安装包解压安装包到目录中 tar -zxvf jdk-8u361-linux-x64.tar.gz如果需要指定目录可以在后面加上 -C,如 tar -zxvf jdk-8u361-linux-x64.tar.gz -C 目录配置jdk环境变量 vim /etc/profile打开…...

native webrtc支持切换音频采集设备和获取裸流
https://www.yuque.com/caokunchao/rtendq/oq8w3qgs3g59whru 前言 版本webrtc m96 1、修改webrtc m96代码,向外提供一个adm指针的接口出来 2、外部来获取指针进行设备的选择 3、外部获取音频裸流,麦克风或者扬声器的数据 修改webrtc代码 1、修改H:\w…...
HR怎么看待PMP证书呢?
在当今竞争激烈的职场环境中,拥有专业的证书已经成为了许多人提升职业竞争力的必要途径。PMP证书作为项目管理领域的国际认证,备受HR和企业的青睐。那么,HR在招聘和评估员工时,究竟是如何看待PMP证书的呢? 首先&#x…...

API接口:如何通过使用手机归属地查询
随着手机普及率的不断增加,手机号码的信息查询也成为了一个非常实用的功能。本文将介绍如何通过使用手机归属地查询API接口实现查询手机号码所在地的功能。 首先,我们需要一个可以查询手机号码所在地的API接口。目前市面上有很多免费或付费的API接口可供…...

小创业公司死亡剧本
感觉蛮真实的;很多小创业公司没有阿里华为的命,却得了阿里华为的病。小的创业公司要想活无非以下几点: 1 现金流,现金流,现金流; 2 产品,找痛点,不要搞伪需求; 3 根据公司…...
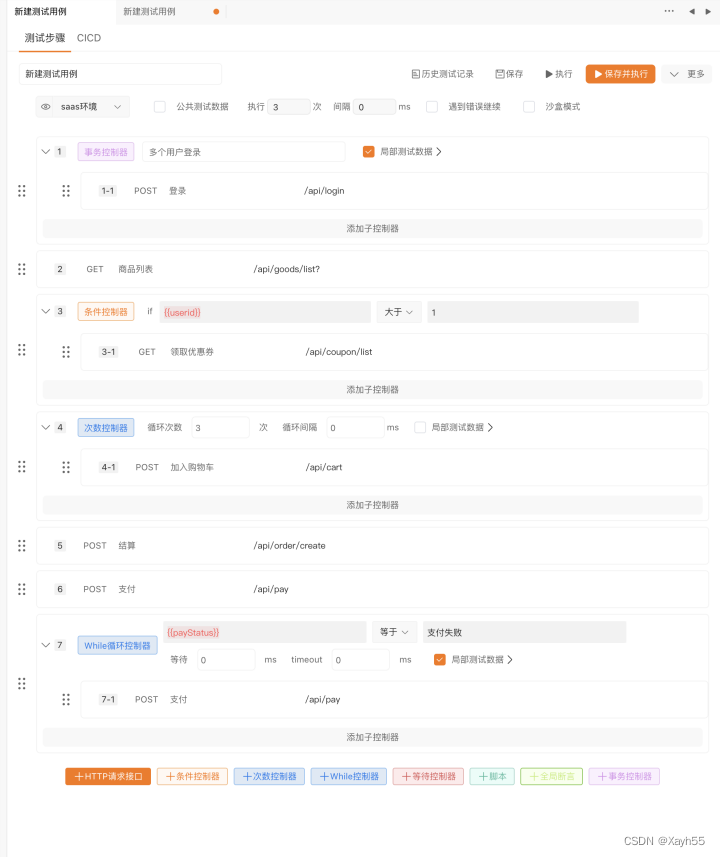
国产化的接口测试、接口自动化测试工具Apipost的介绍及使用
Apipost介绍: Apipost是 API 文档、API 调试、API Mock、API 自动化测试一体化的研发协作赋能平台,它的定位 Postman Swagger Mock JMeter。 Apipost 是接口管理、开发、测试全流程集成工具,能支撑整个研发技术团队同平台工作࿰…...
【MySQL】不允许你不知道如何插入数据
🎬 博客主页:博主链接 🎥 本文由 M malloc 原创,首发于 CSDN🙉 🎄 学习专栏推荐:LeetCode刷题集 🏅 欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正࿰…...
Vue 渲染流程详解
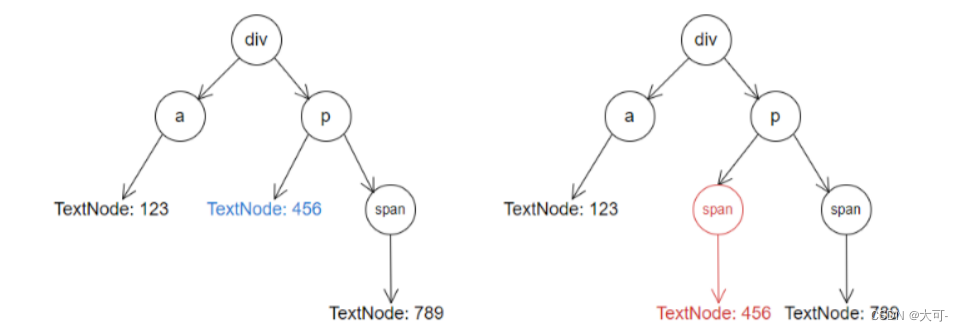
在 Vue 里渲染一块内容,会有以下步骤及流程: 第一步,解析语法,生成AST 第二步,根据AST结果,完成data数据初始化 第三步,根据AST结果和DATA数据绑定情况,生成虚拟DOM 第四步&…...
10分钟内入门 ArcGIS Pro
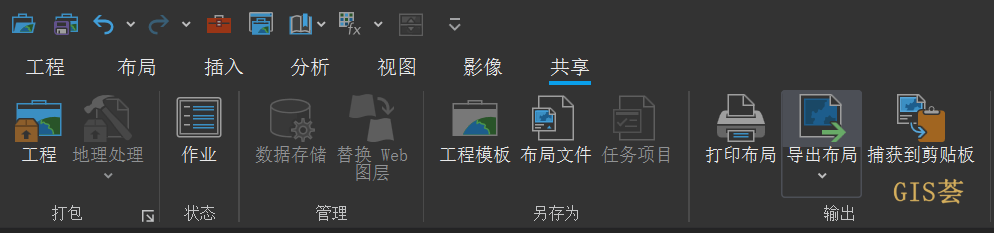
本文来源:GIS荟 大家好,这篇文章大概会花费你10分钟的时间,带你入门 ArcGIS Pro 的使用,不过前提是你有 ArcMap 使用经验。 我将从工程文件组织方式、软件界面、常用功能、编辑器、制图这5个维度给大家介绍。 演示使用的 ArcGI…...
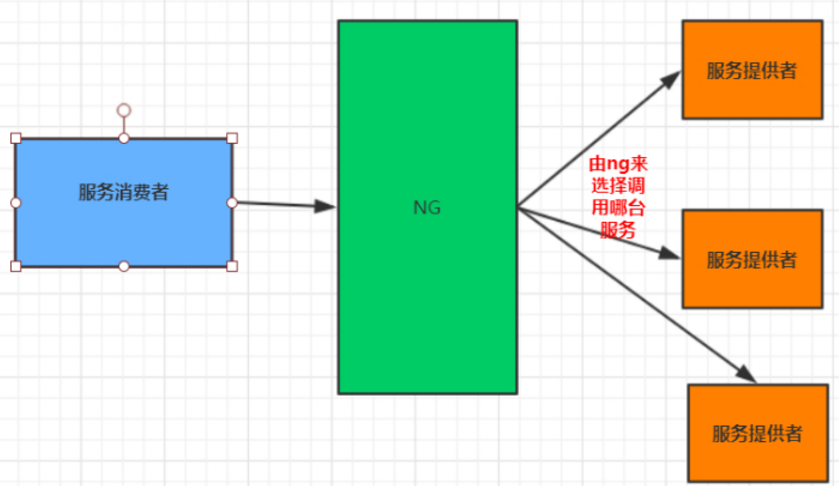
【ribbon】Ribbon的使用与原理
负载均衡介绍 负载均衡(Load Balance),其含义就是指将负载(工作任务)进行平衡、分摊到多个操作单元上进行运行,例如FTP服务器、Web服务器、企业核心应用服务器和其它主要任务服务器等,从而协同…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...
