【数据结构】24王道考研笔记——图
六、图
目录
- 六、图
- 定义及基本术语
- 图的定义
- 有向图以及无向图
- 简单图以及多重图
- 度
- 顶点-顶点间关系
- 连通图、强连通图
- 子图
- 连通分量
- 强连通分量
- 生成树
- 生成森林
- 边的权、带权网/图
- 特殊形态的图
- 图的存储及基本操作
- 邻接矩阵
- 邻接表法
- 十字链表
- 邻接多重表
- 分析对比
- 图的基本操作
- 图的遍历
- 广度优先遍历(BFS)
- 深度优先遍历(DFS)
- 图的应用
- 最小生成树
- 最短路径BFS
- 最短路径Dijkstra
- 最短路径Floyd算法
- 有向无环图
- 拓扑排序
- 关键路径
定义及基本术语
图的定义

有向图以及无向图

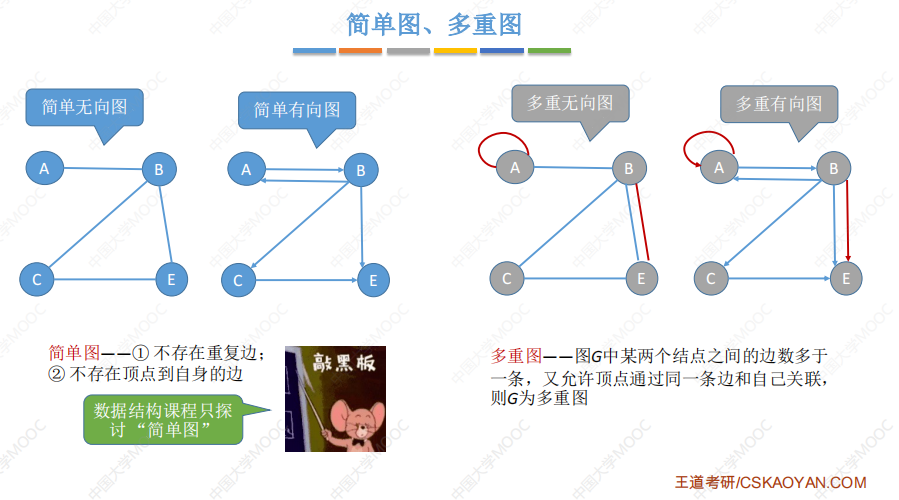
简单图以及多重图
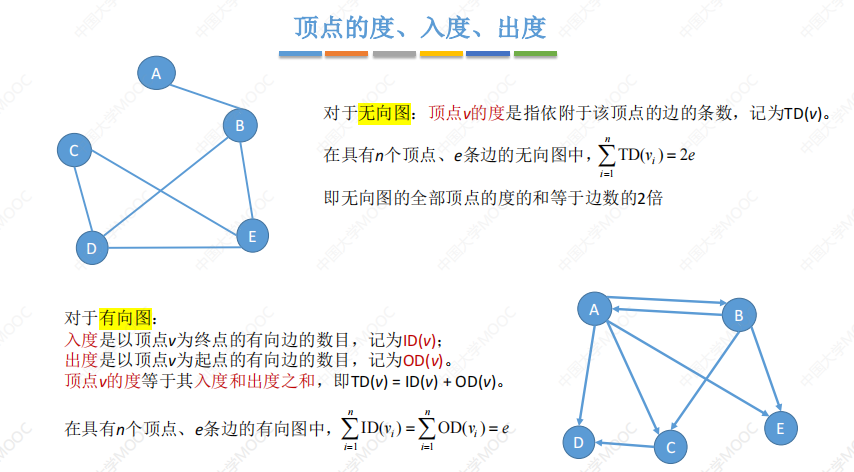
度
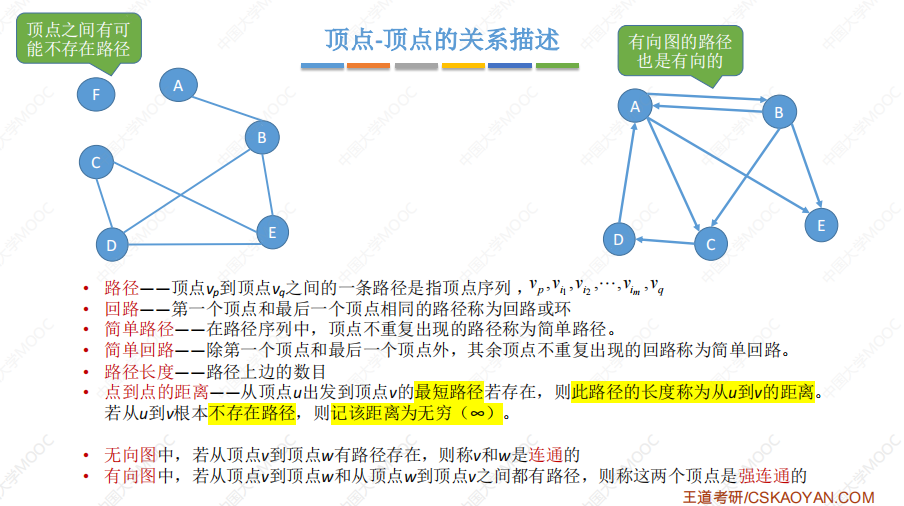
顶点-顶点间关系
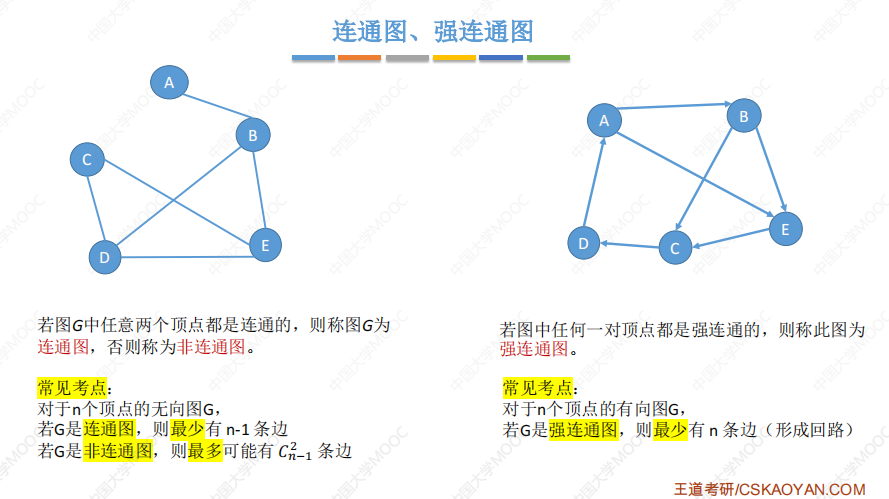
连通图、强连通图
子图
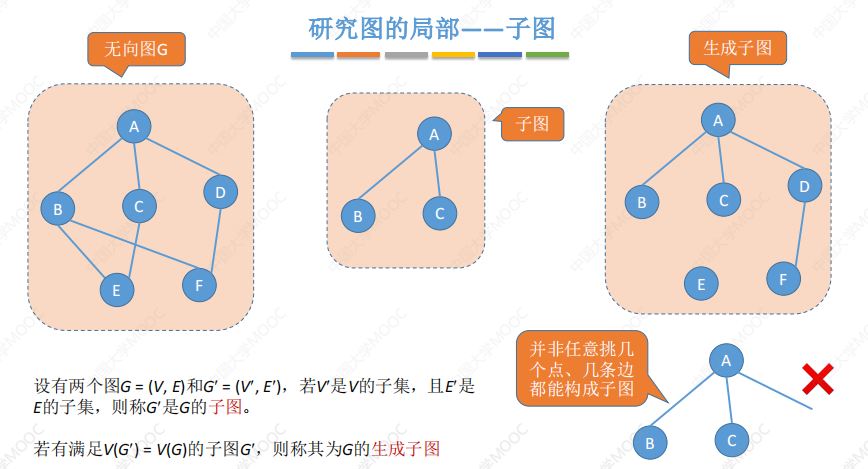
(有向图也一样)
连通分量

强连通分量
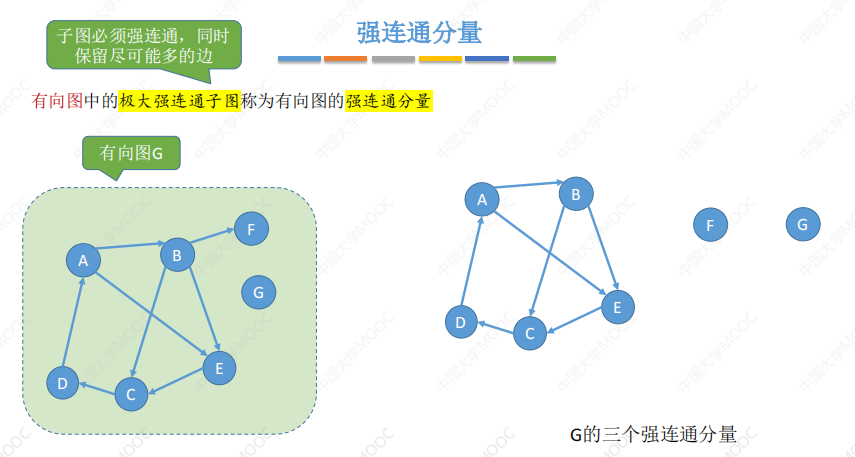
生成树
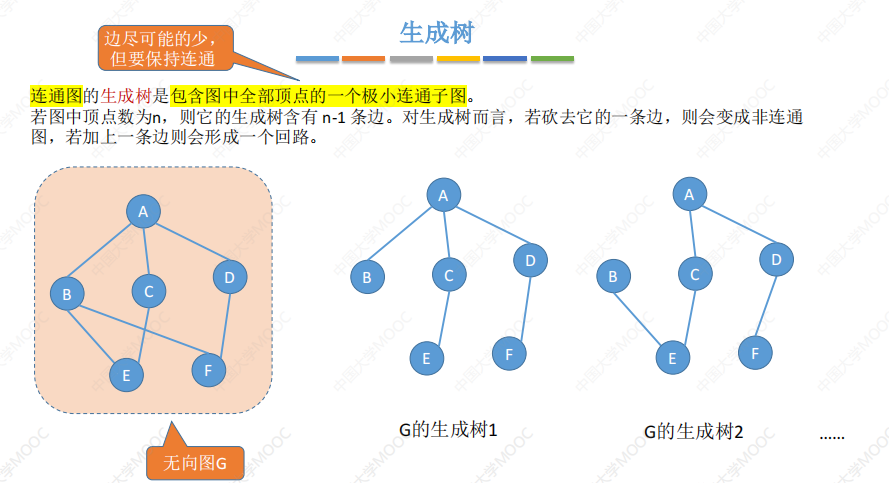
生成森林
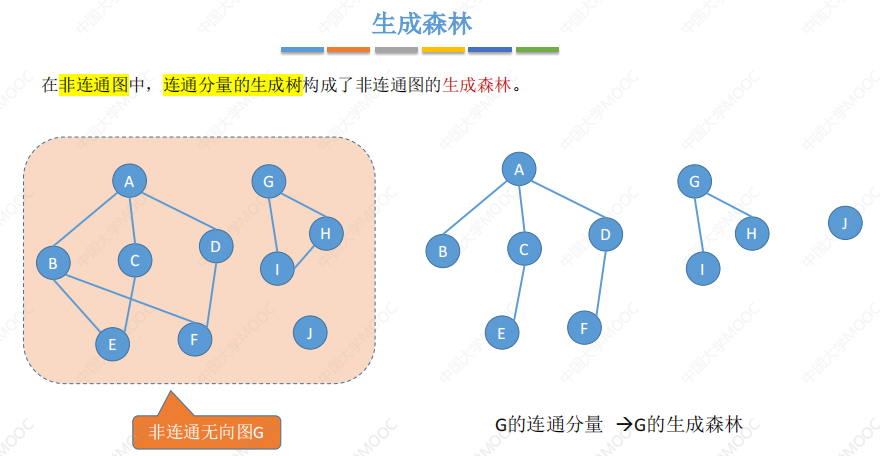
边的权、带权网/图
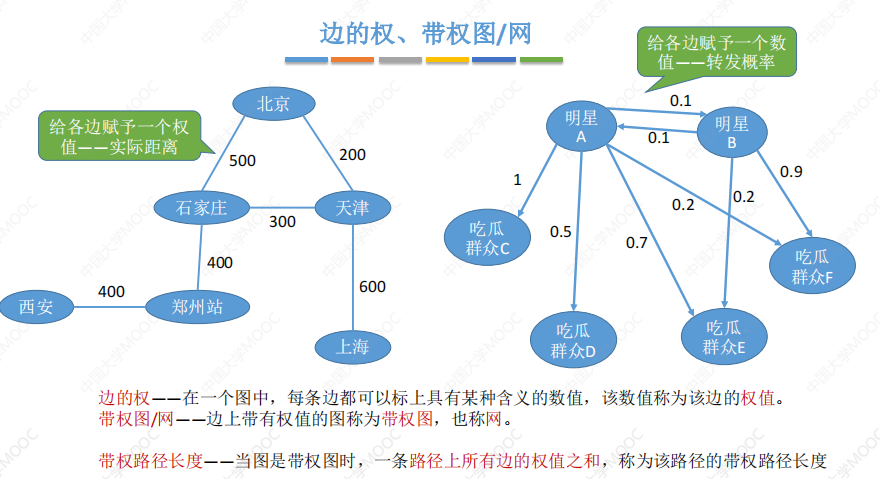
特殊形态的图

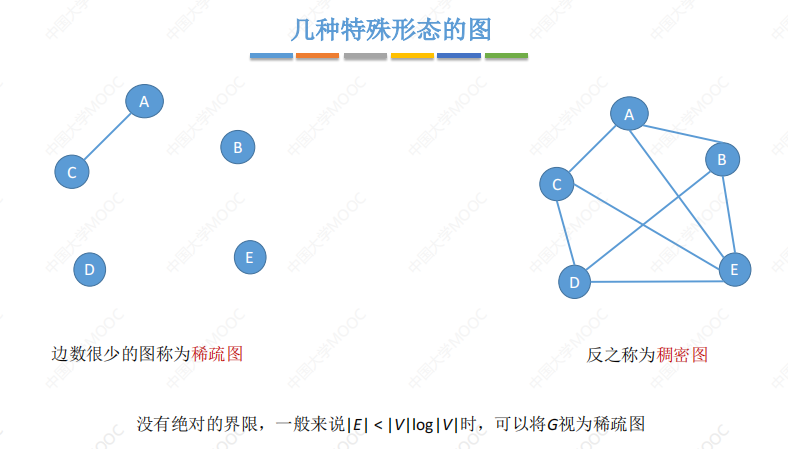
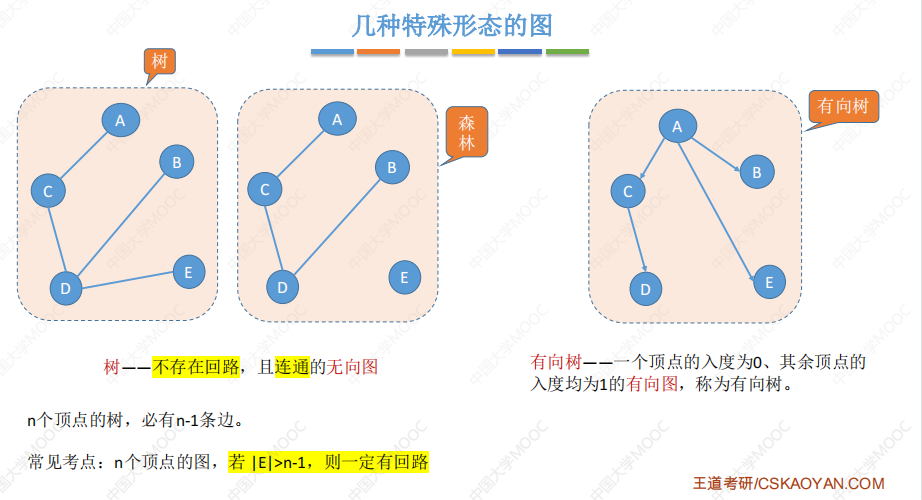
总结:

图的存储及基本操作
邻接矩阵
#define MaxVertexNum 100//顶点数目的最大值
typedef struct
{char Vex[MaxVertexNum];//顶点表 (可存更复杂的信息)int Edge[MaxVertexNum][MaxVertexNum];//邻接矩阵,边表(可以用bool型或枚举型变量表示边)int vexnum, arcnum;//图的当前顶点数和边数/弧数
}MGraph;
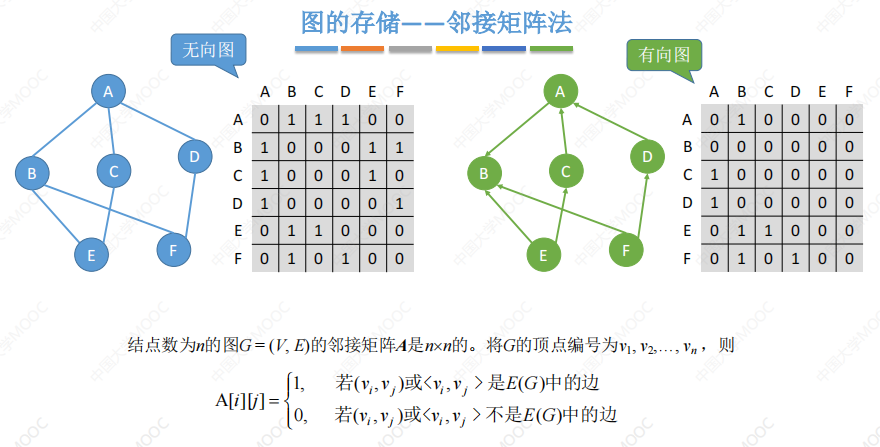

存储带权图(网):

对角线处可以填0或∞
空间复杂度为O(|V|2)只和顶点数相关,和实际的边数无关,适合用于存储稠密图
对于无向图,邻接矩阵是对称矩阵,可以进行对称矩阵的存储压缩,存入一维数组中(只存储上三角区/下三角区)
性质:
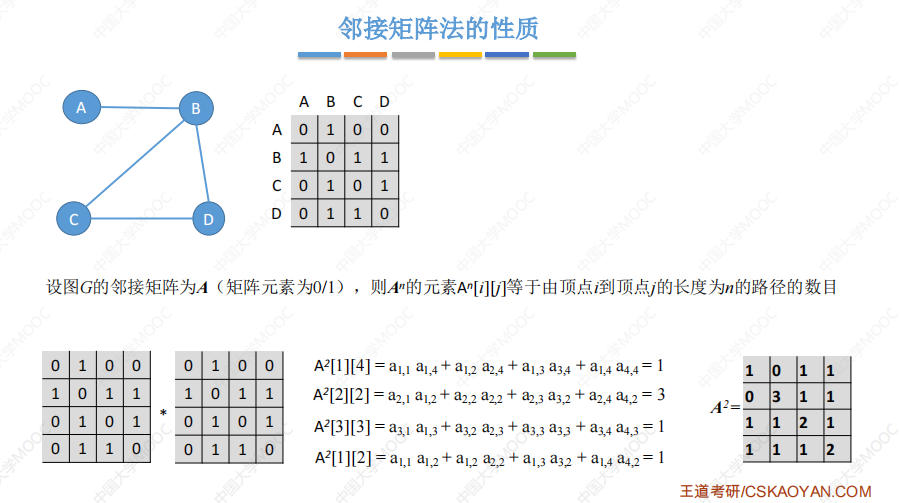
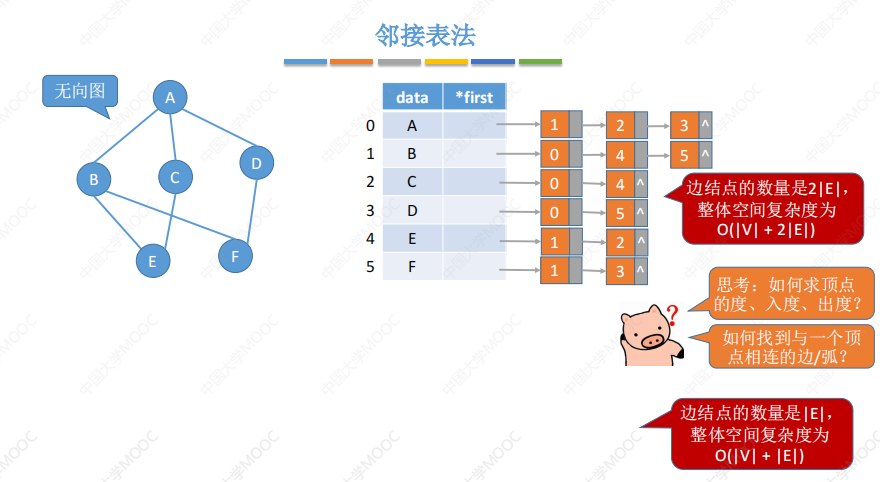
邻接表法
邻接矩阵是用数组实现的顺序存储,空间复杂度高,不适合存储稀疏图
而邻接表法使用顺序+链式存储的方式,表示方式并不唯一(与树的孩子表示法相似)
//邻接表
typedef char VertexType;//顶点的数据类型
//“边/弧”
typedef struct ArcNode
{int adjvex;//边/弧指向哪个节点struct ArcNode* next;//指向下一条弧的指针//InfoType info;//权值
}ArcNode;
//“顶点”
typedef struct VNode
{VertexType data;//顶点信息ArcNode* first;//第一条边/弧
}VNode,AdjList[MaxVertexNum];
//用邻接表存储的图
typedef struct
{AdjList vertices;int vexnum, arcnum;
}ALGraph;
与邻接矩阵对比:

十字链表
用邻接矩阵以及邻接表存储有向图时,都有所缺陷:

使用十字链表存储有向图(不能用于无向图):

空间复杂度为:O(|V|+|E|)
顺着绿色路线能找到顶点所有的出边
顺着橙色路线能找到顶点所有的入边
邻接多重表
用邻接矩阵以及邻接表存储无向图时,都有所缺陷:
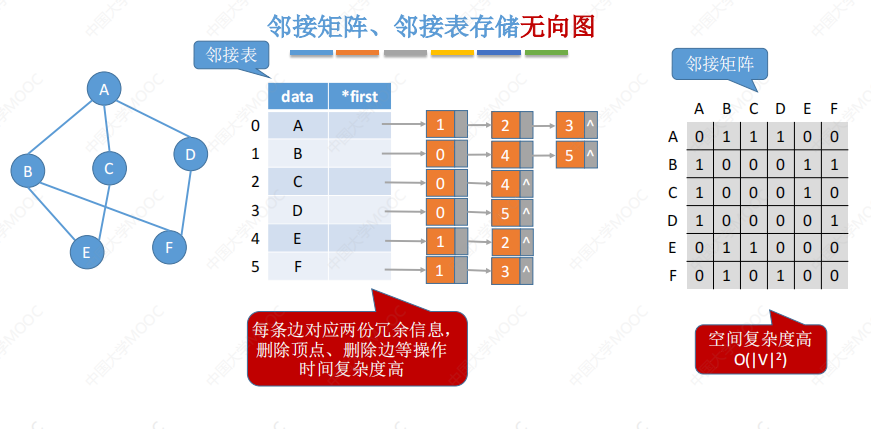
用邻接多重表存储无向图(不能用于有向图):
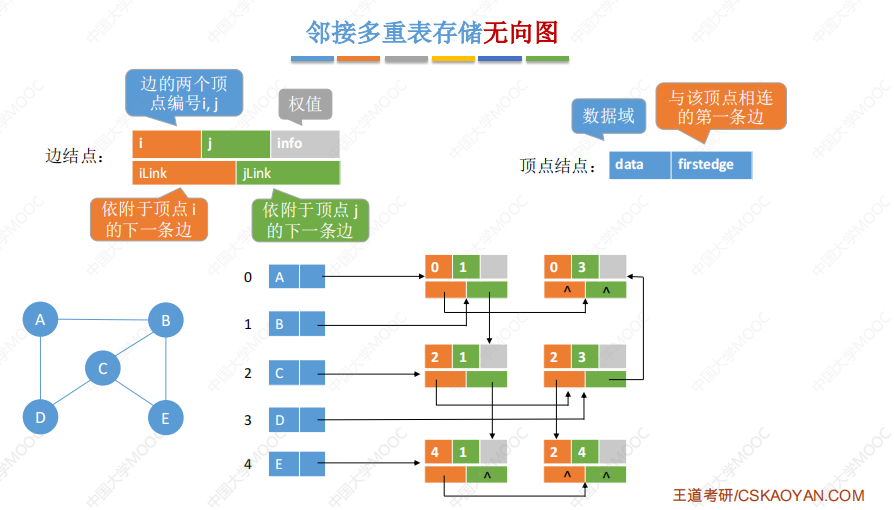
空间复杂度:O(|V|+|E|)
删除边、删除节点等操作很方便
分析对比

图的基本操作
主要基于图的邻接矩阵以及邻接表

**Adjacent(G,x,y):**判断图G是否存在边<x, y>或(x, y)。
邻接矩阵:O(1) 邻接表:O(1)~O(|V|)
**Neighbors(G,x):**列出图G中与结点x邻接的边。
邻接矩阵:O(|V|) 邻接表:出边:O(1)~O(|V|) 入边:O(|E|)
**InsertVertex(G,x):**在图G中插入顶点x
邻接矩阵:O(1) 邻接表:O(1)
**DeleteVertex(G,x):**从图G中删除节点x
邻接矩阵:O(|V|) 邻接表:出边:O(1)~O(|V|) 入边:O(|E|)
**AddEdge(G,x,y):**若无向边(x, y)或有向边<x, y>不存在,则向图G中添加该边。
邻接矩阵:O(1) 邻接表:O(1)
**RemoveEdge(G,x,y):**若无向边(x, y)或有向边<x, y>存在,则从图G中删除该边。
邻接矩阵:O(1) 邻接表:O(1)~O(|V|)
**FirstNeighbor(G,x):**求图G中顶点x的第一个邻接点,若有则返回顶点号。若x没有邻接点或图中不存在x,则返回-1。
邻接矩阵:O(1)~O(|V|) 邻接表:出边:O(1) 入边:O(1)~O(|E|)
**NextNeighbor(G,x,y):**假设图G中顶点y是顶点x的一个邻接点,返回除y之外顶点x的下一个邻接点的顶点号,若y是x的最后一个邻接点,则返回-1。
邻接矩阵:O(1)~O(|V|) 邻接表:O(1)
图的遍历
广度优先遍历(BFS)
实现思路:
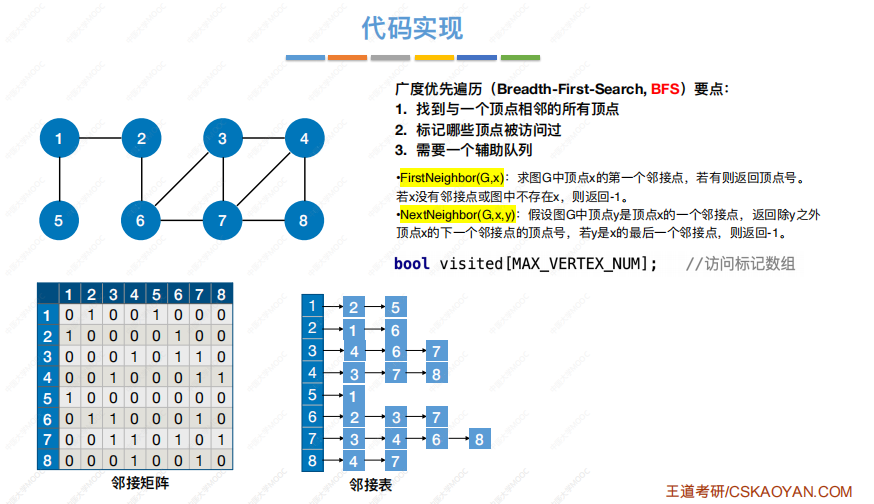
#define MAX_VERTEX_NUM 100//顶点数目的最大值bool visited[MAX_VERTEX_NUM];//访问标记数组
void BFSTraverse(Graph G) //对图G进行广度优先遍历
{for (int i = 0; i < G.vexnum; ++i)visited[i] = false;//访问标记数组初始化InitQueue(Q);//初始化辅助队列Qfor (int i = 0; i < G.vexnum; ++i)//从0号顶点开始遍历{if (!visited[i])//对每个连通分量调用一次BFSBFS(G, i);//vi未访问过,从vi开始BFS}
}//广度优先遍历
void BFS(Graph G, int v) //从顶点v出发,广度优先遍历图G
{visit(v);//访问初始顶点vvisited[v] = true;//对v做已访问标记Enqueue(Q, v);//顶点v入队列Qwhile (!isEmpty(Q)){DeQueue(Q, v);//顶点v处队列for (w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)){//检测v所有邻接点if (!visited[w])//w为v的尚未访问的邻接顶点{visit(w);//访问顶点wvisited[w] = true;//对w做已访问标记EnQueue(Q, w);//顶点w入队列}}}
}
遍历序列是具有可变性的
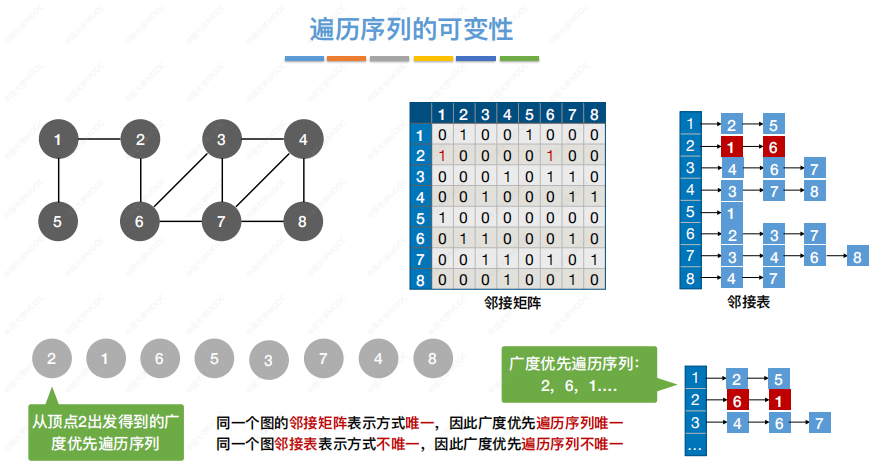
对于无向图,调用BFS函数的次数=连通分量数
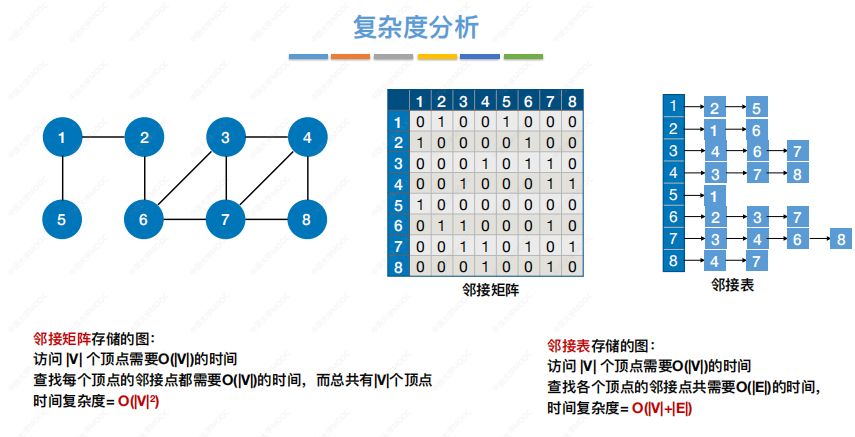
复杂度分析:

广度优先生成树(若是非连通图,则得到广度优先生成森林)
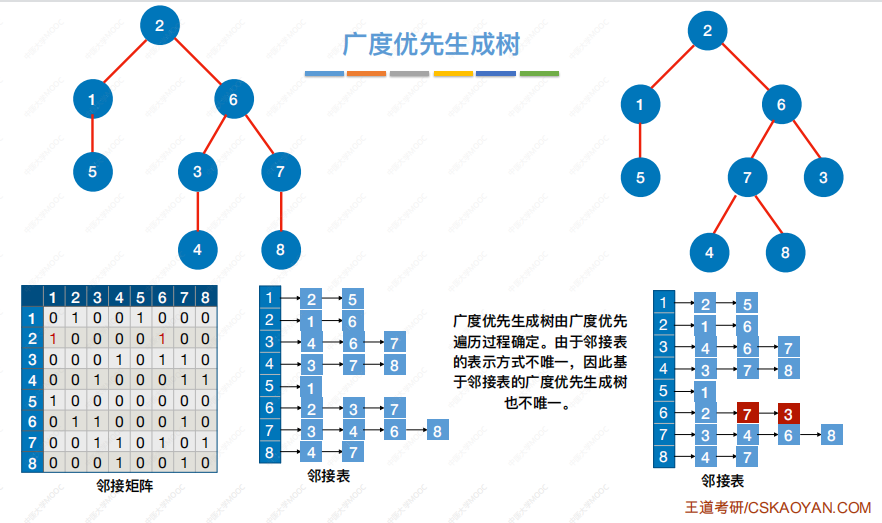
利用广度优先生成的树,高度是最小的(因为按最短路径)
应用:解决非带权图的单源最短路径问题
//解决非带权图的单源最短路径问题
void BFS_MIN_Distance(Graph G, int u)
{//d[i]表示从u到i结点的最短路径for (int i = 0; i < G.vexnum; ++i){d[i] = 0x3f3f3f3f;//无穷大,初始化路径长度}visited[u] = true;d[u] = 0;EnQueue(Q, u);while (!isEmpty(Q))//BFS算法主过程{DeQueue(Q, u);//队头元素u出队for (w = FirstNeighbor(G, u); w >= 0; w = NextNeighbor(G, u, w)){if (!visited[w])//w为u的尚未访问的邻接顶点{visited[w] = true;//设已访问标记d[w] = d[u] + 1;//路径长度加1EnQueue(Q, w);//顶点w入队}}}
}
深度优先遍历(DFS)
类似于树的先根遍历,使用函数调用栈,递归实现
#define MAX_VERTEX_NUM 100//顶点数目的最大值bool visited[MAX_VERTEX_NUM];//访问标记数组void DFSTraverse(Graph G)//深度优先遍历图G
{for (v = 0; v < G.vexnum; ++v)visited[v] = false;//初始化已访问标记数据for (v = 0; v < G.vexnum; ++v)//从v=0开始遍历if (!visited[v])DFS(G, v);
}void DFS(Graph G, int v)//从顶点v触发,深度优先遍历图G
{visit(v);//访问顶点vvisited[v] = true;//设已访问标记for (w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)){if (!visited[w]){DFS(G, w); // w为v的尚未访问的邻接顶点}}
}
复杂度分析:

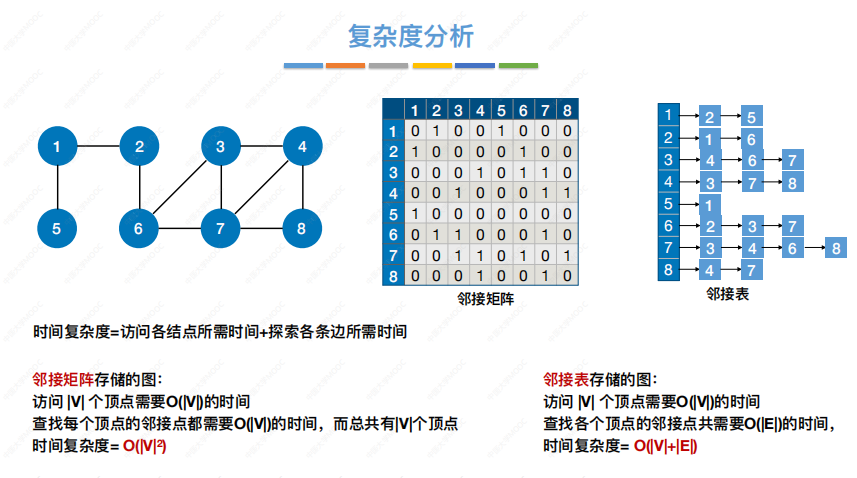
遍历序列不唯一性:
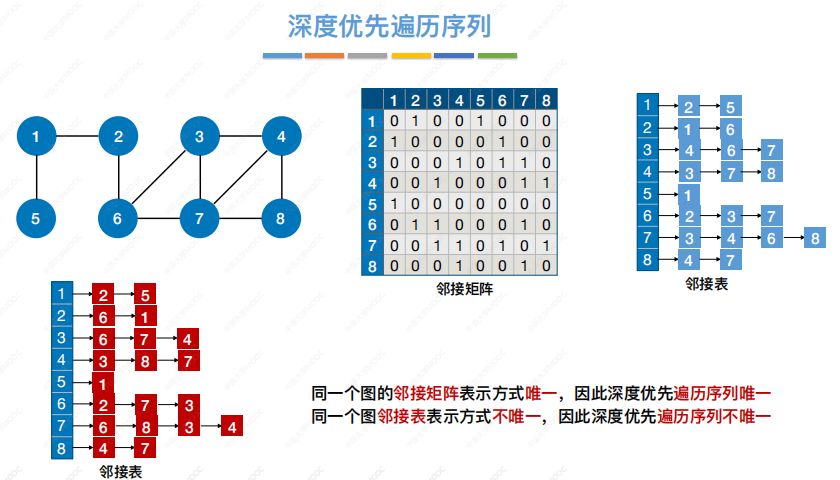
深度优先生成树:(非连通生成森林)

对于无向图进行BFS/DFS遍历,调用BFS/DFS次数=连通分量数,对于连通图,只调用一次
对于有向图进行BFS/DFS遍历,调用BFS/DFS次数要具体问题具体分析,若起始顶点到其他各顶点都有路径,只调用一次,对于强连通图,从任一结点出发都只需调用一次BFS/DFS
图的应用
最小生成树
连通图的生成树是包含图中全部顶点的一个极小连通子图。若图中顶点数为n,则它的生成树含有n-1条边,对生成树而言,若砍去它的一条边,则会变成非连通图,若加上一条边则会形成一个回路。
广度优先生成树的高度是小于等于深度优先生成树的高度的。
最小生成树定义:

两种求最小生成树的方法:
Kruskal:

Prim:
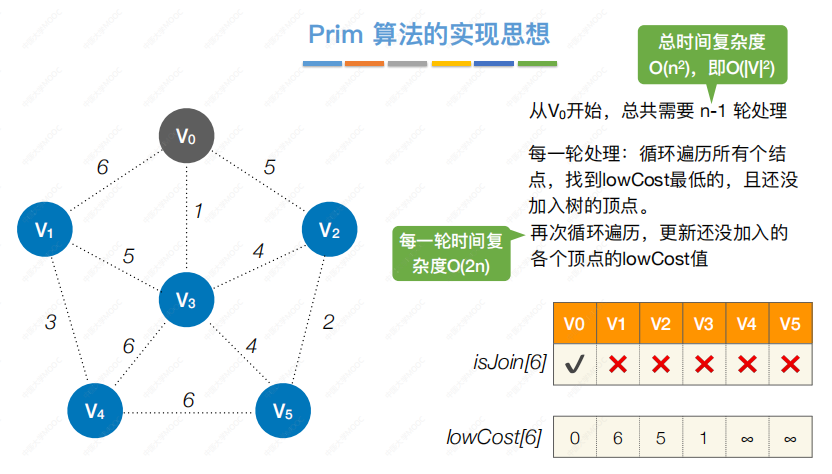

最短路径BFS
最短路径问题描述:
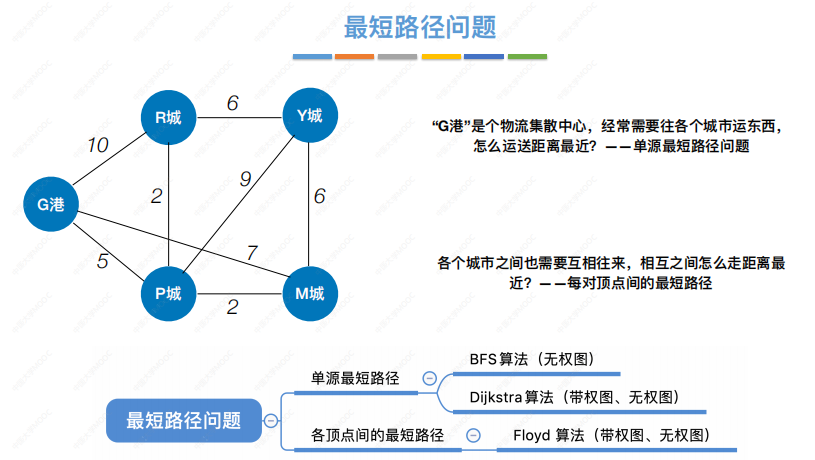
利用BFS算法可以求无权图的单源最短路径(无权图可以视作一种特殊的带权图,只是每条边的权值都为1)故各边权值相等时,可以使用BFS算法求解
代码实现:
//解决非带权图的单源最短路径问题
void BFS_MIN_Distance(Graph G, int u)
{//d[i]表示从u到i结点的最短路径for (int i = 0; i < G.vexnum; ++i){d[i] = 0x3f3f3f3f;//无穷大,初始化路径长度path[i]=-1;//记录最短路径从哪个顶点过来}visited[u] = true;d[u] = 0;EnQueue(Q, u);while (!isEmpty(Q))//BFS算法主过程{DeQueue(Q, u);//队头元素u出队for (w = FirstNeighbor(G, u); w >= 0; w = NextNeighbor(G, u, w)){if (!visited[w])//w为u的尚未访问的邻接顶点{visited[w] = true;//设已访问标记d[w] = d[u] + 1;//路径长度加1path[w]=u;//最短路径应从u到wEnQueue(Q, w);//顶点w入队}}}
}
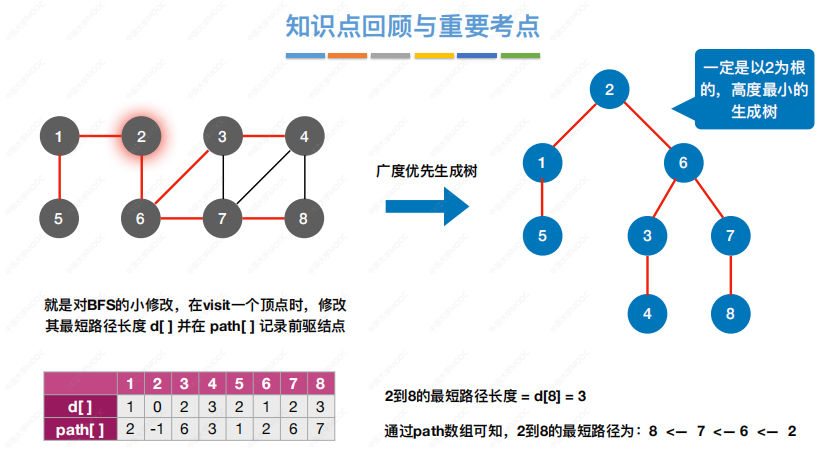
时间复杂度:邻接矩阵O(|V|2) 邻接表O(|V|+|E|)
最短路径Dijkstra
dist[ ]记录从源点v0到其他各顶点当前的最短路径长度,它的初态为:若从v0到vi有弧,则dist[i]为弧上的权值,否则置于∞
path[ ]表示从源点到顶点i之间的最短路径的前驱结点。在算法结束时,可根据其值追溯得到源点v0到顶点vi的最短路径。

不适用于有负权值的带权图
用邻接矩阵以及邻接表时间复杂度都为O(|V|2)
最短路径Floyd算法
算法思路:


最终实现:

对于更多结点,若要找到完整路径需要通过path矩阵递归寻找

Floyd算法可以用于负权图,但不能解决带有“负权回路”的图(有负权值的边组成回路)这种图有可能没有最短路径
不同算法对比:

有向无环图
若一个有向图中不存在环,则称为有向无环图,简称DAG图
有向无环图是描述含有公共子式的表达式的有效工具
其表示表达式中顶点中不可能出现重复的操作数
步骤:
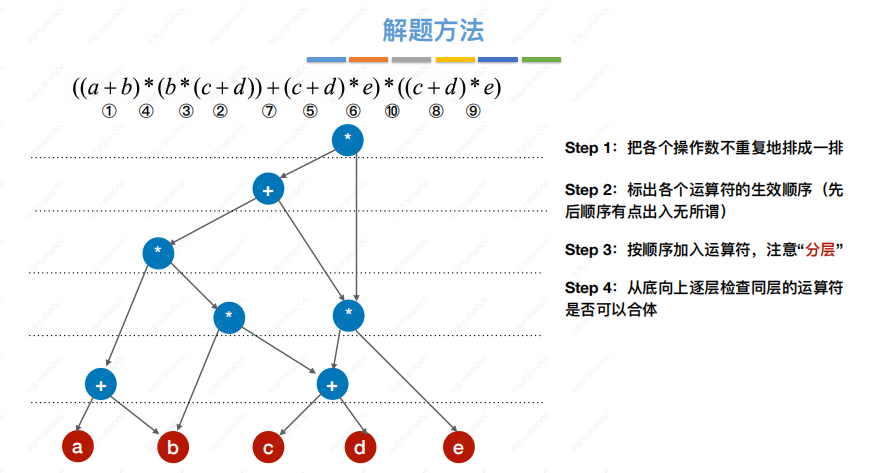
表示出来的结果可能不唯一
拓扑排序
AOV网:用DAG图表示一个工程,顶点表示活动,有向边<Vi,Vj>表示活动Vi必须先于活动Vj进行,不能存在环路!
拓扑排序:


实现代码:
#define MaxVertexNum 100//图中顶点数目的最大值//定义邻接表
typedef char VertexType;//顶点的数据类型
//“边/弧”
typedef struct ArcNode
{int adjvex;//边/弧指向哪个节点struct ArcNode* nextarc;//指向下一条弧的指针//InfoType info;//权值
}ArcNode;
//“顶点”
typedef struct VNode
{VertexType data;//顶点信息ArcNode* firstarc;//第一条边/弧
}VNode, AdjList[MaxVertexNum];
//用邻接表存储的图
typedef struct
{AdjList vertices;int vexnum, arcnum;
}ALGraph;//拓扑排序
bool TopologicalSort(Graph G)
{InitStack(S);//初始化栈,存储入度为0的结点for (int i = 0; i < G.vexnum; i++){if (indegree[i] == 0){Push(S, i);//将所有入度为0的顶点进栈}}int count = 0;//计数,记录当前已经输出的顶点数while (!IsEmpty(S))//栈不空,则存在入度为0的顶点{Pop(S, i);//栈顶元素出栈print(count++) = i;//输出顶点ifor (p = G.vertices[i].firstarc; p; p = p->nextarc){//将所有i指向的顶点的入度减1,并且将入度为0的顶点压入栈Sv = p->adjvex;if (!(--indegree[v]))//若为0{Push(S, v);//入栈}}}if (count < G.vexnum){return false;//排序失败,有向图中有回路}elsereturn true;//拓扑排序成功
}
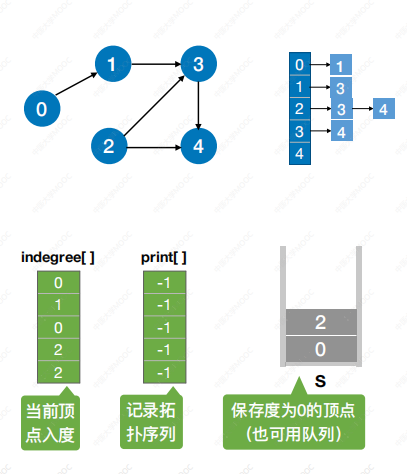
时间复杂度:邻接表:O(|V|+|E|) 若采用邻接矩阵 O(|V|2)
逆拓扑排序:

也可以用DFS算法实现:
//逆拓扑排序
void DFSTraverse(Graph G)//深度优先遍历图G
{for (v = 0; v < G.vexnum; ++v)visited[v] = false;//初始化已访问标记数据for (v = 0; v < G.vexnum; ++v)//从v=0开始遍历if (!visited[v])DFS(G, v);
}void DFS(Graph G, int v)//从顶点v触发,深度优先遍历图G
{visit(v);//访问顶点vvisited[v] = true;//设已访问标记for (w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)){if (!visited[w]){DFS(G, w); // w为v的尚未访问的邻接顶点}}print(v);//输出顶点
}
关键路径
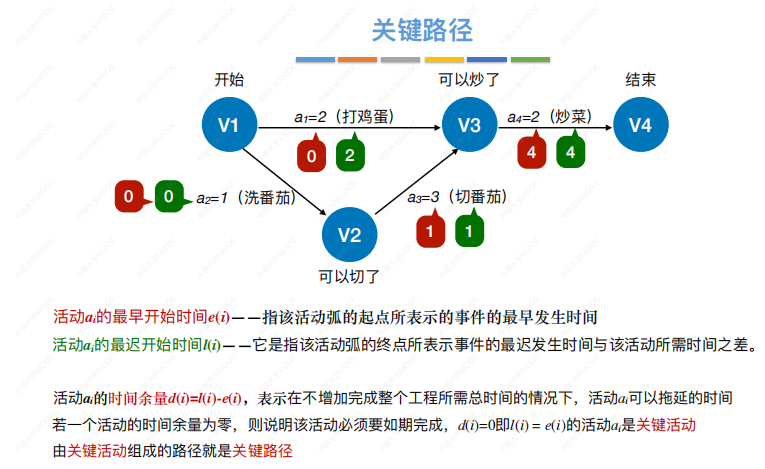
在带权有向图中,以顶点表示事件,以有向边表示活动,以边上的权值表示完成该活动的开销(如完成活动所需的时间),称之为用边表示活动的网络,简称AOE网。
性质:

AOE网中仅有一个入度为0的顶点,称为开始顶点(源点),也仅有一个出度为0的顶点,称为结束顶点(汇点)
从源点到汇点的有向路径可能有多条,所有路径中,具有最大路径长度的路径称为关键路径,而把关键路径上的活动称为关键活动
完成整个工作的最短时间就是关键路径的长度,若关键活动 不能按时安成为,则整个工程的完成时间就会延长。
几个概念:
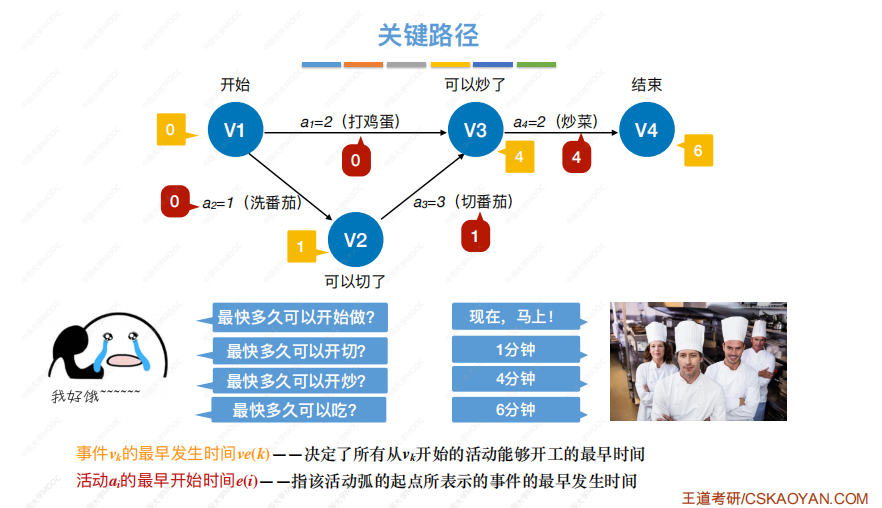

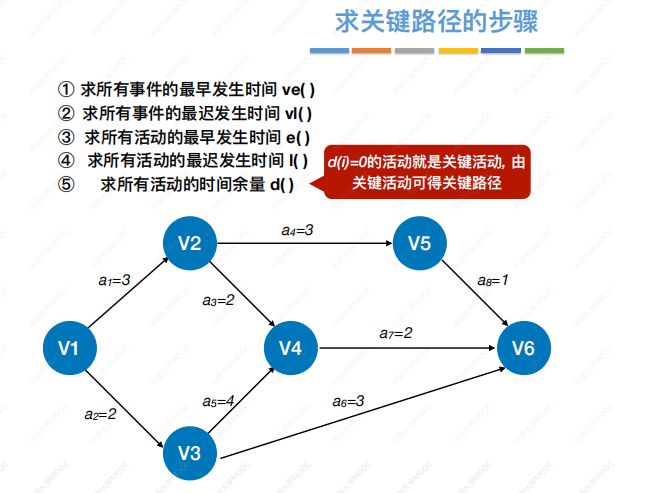
求关键路径的步骤:
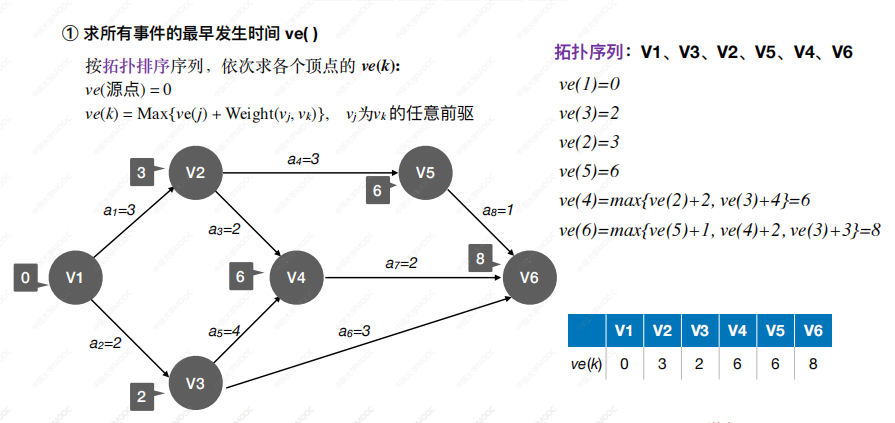
求事件的最早发生时间:
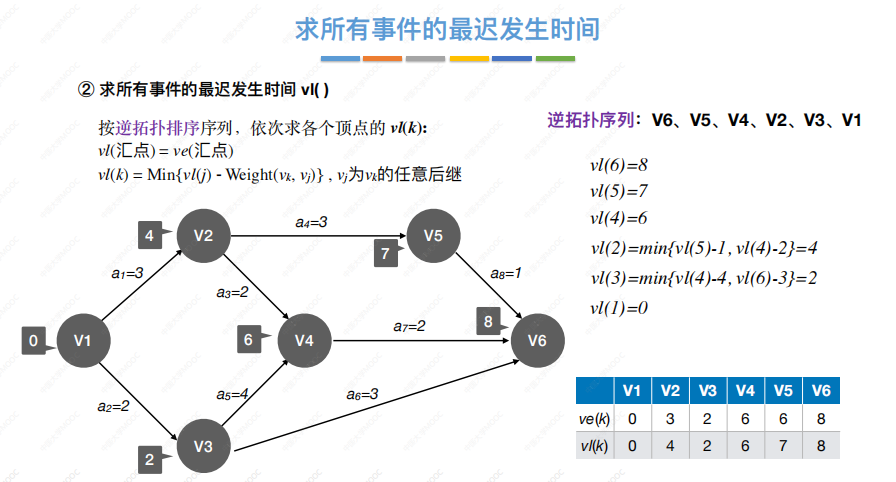
求事件的最迟发生时间:
求活动的最早发生时间:
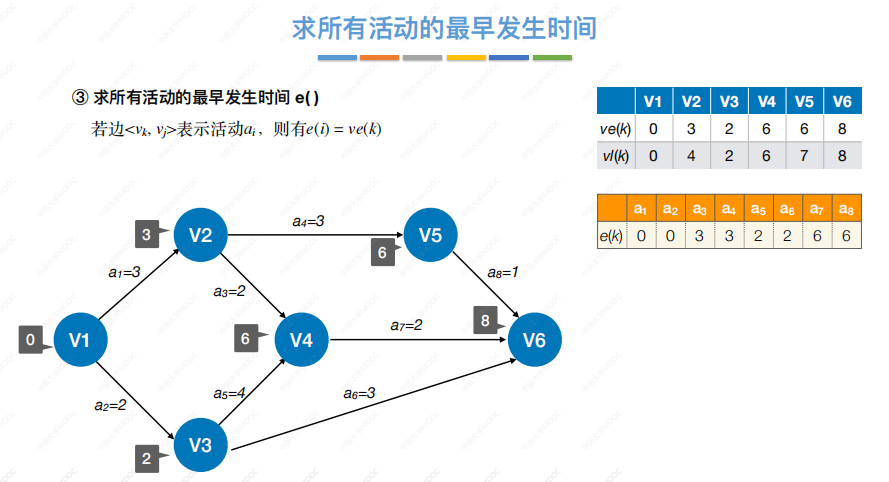
求活动的最迟发生时间:
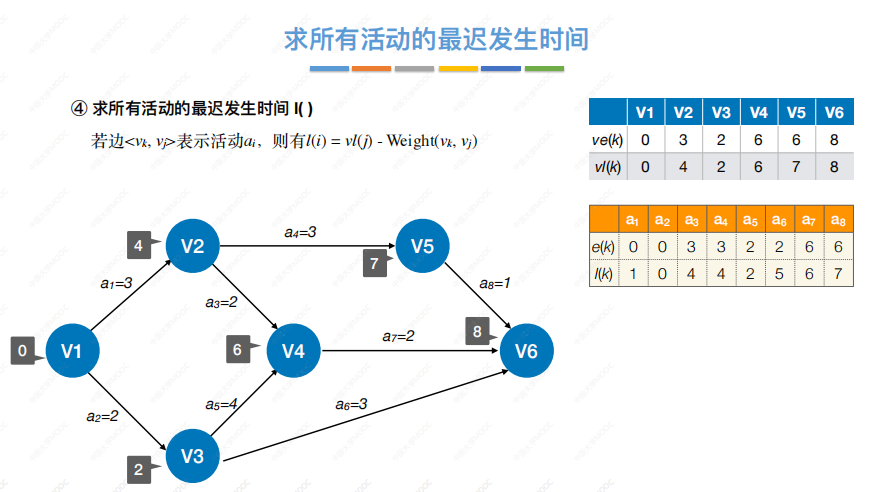
求活动的时间余量:
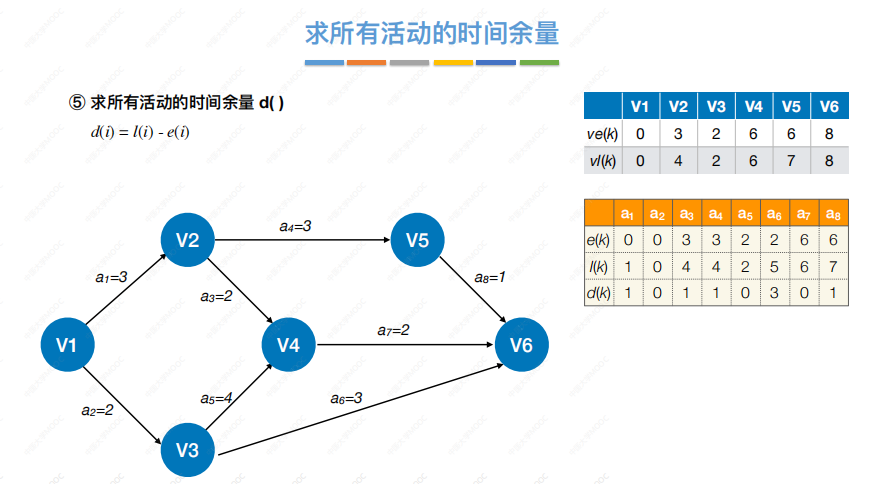
最终得出关键路径:

特性:
若关键活动耗时增加,则整个工程的工期将增长,缩短关键活动的时间,可以缩短整个工程的工期,当缩短到一定程度时,关键活动可能会变成非关键活动。
可能有多条关键路径,只提高一条关键路径上的关键活动速度并不能缩短整个工程的工期,只有加快那些包括在所有关键路径上的关键活动才能达到缩短工期的目的。
思路总结:

主要参考:王道考研课程
后续会持续更新考研408部分的学习笔记,欢迎关注。
github仓库(含所有相关源码):408数据结构笔记
相关文章:

【数据结构】24王道考研笔记——图
六、图 目录 六、图定义及基本术语图的定义有向图以及无向图简单图以及多重图度顶点-顶点间关系连通图、强连通图子图连通分量强连通分量生成树生成森林边的权、带权网/图特殊形态的图 图的存储及基本操作邻接矩阵邻接表法十字链表邻接多重表分析对比图的基本操作 图的遍历广度…...
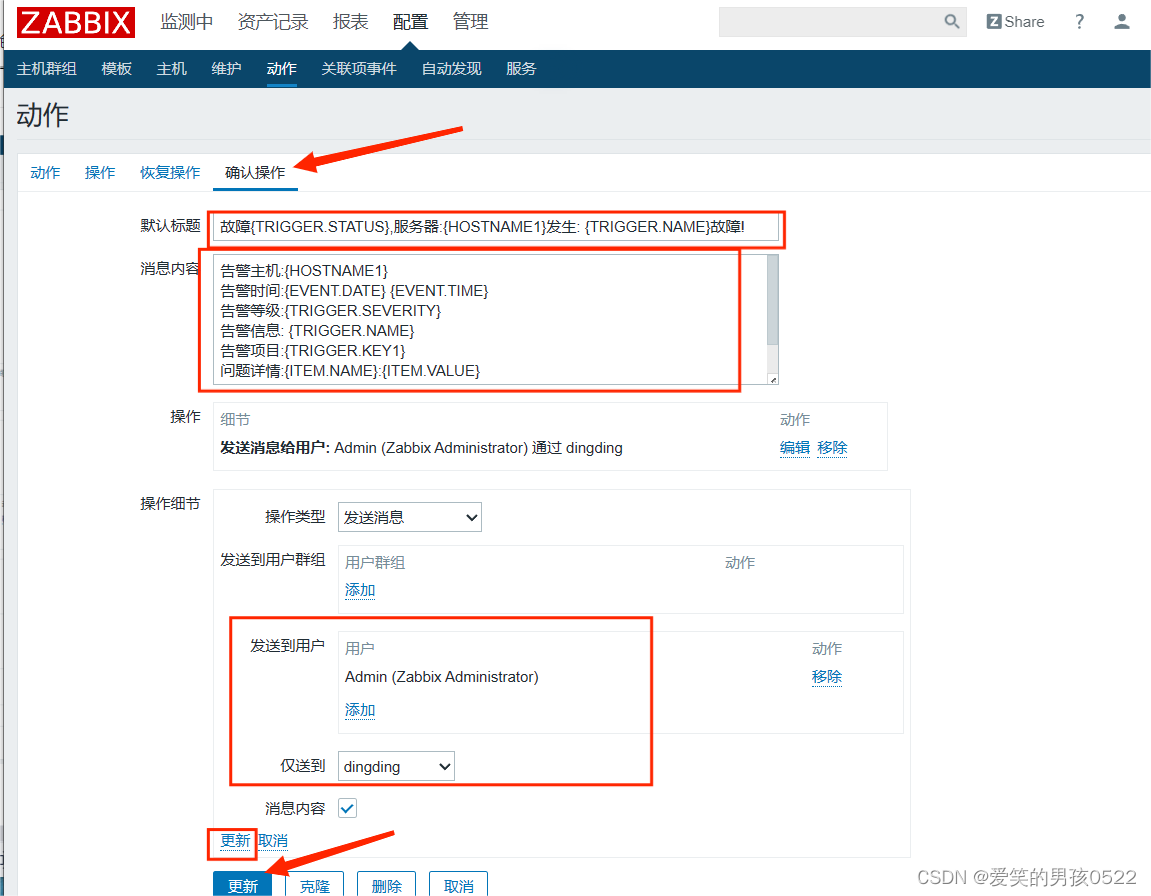
zabbix钉钉报警
登录钉钉客户端,创建一个群,把需要收到报警信息的人员都拉到这个群内. 然后点击群右上角 的"群机器人"->"添加机器人"->"自定义", 记录该机器人的webhook值。 添加机器人 在钉钉群中,找到只能群助手 添加机器人 选择自定义机…...
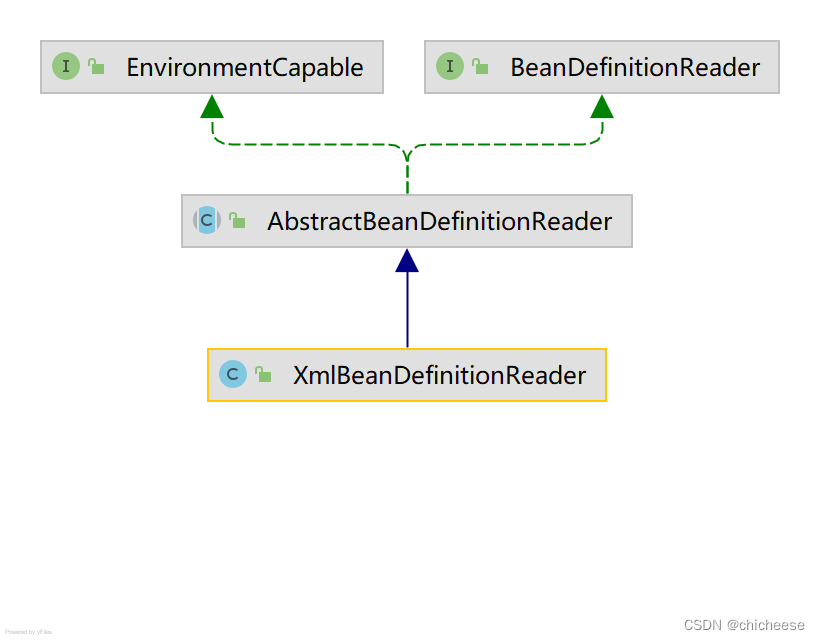
Spring 源码解读
1、Spring 的结构组成 1.1、核心类介绍 Spring 中有两个最核心的类 1 DefaultListableBeanFactory XmlBeanFactory 继承自 DefaultListableBeanFactory,而DefaultListableBeanFactory 是整个 bean加载的核心部分,是 Spring 注册及加载 bean 的默认实现…...
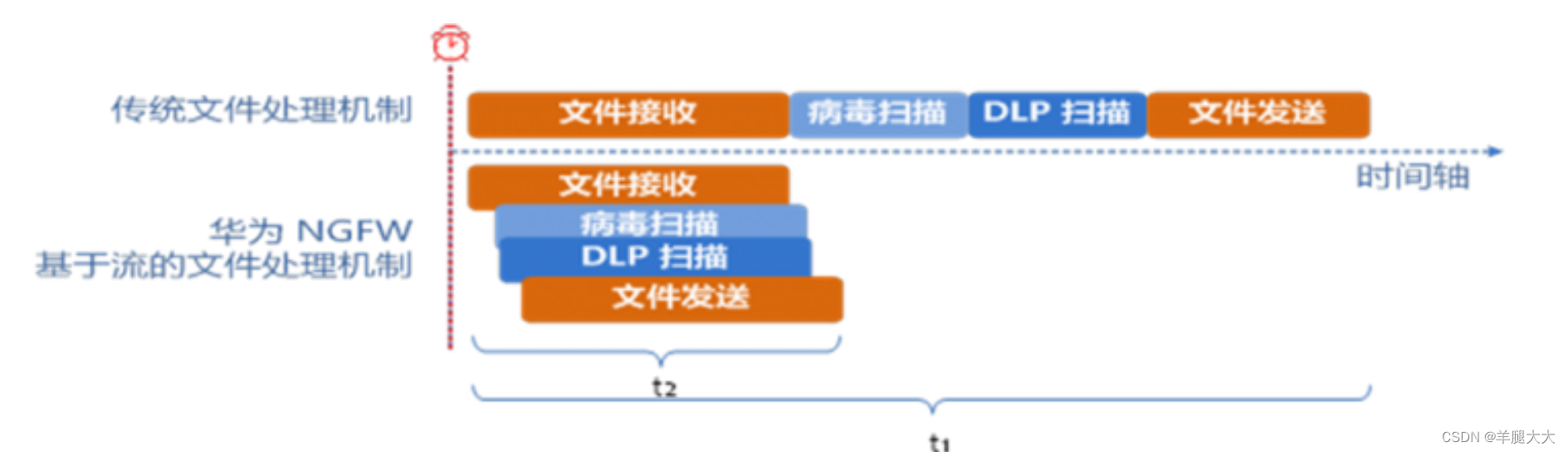
练习时长两年半的网络安全防御“first”
1.网络安全常识及术语 下边基于这次攻击演示我们介绍一下网络安全的一些常识和术语。 资产 任何对组织业务具有价值的信息资产,包括计算机硬件、通信设施、 IT 环境、数据库、软件、文档资料、信息服务和人员等。 网络安全 网络安全是指网络系统的硬件、软件及…...

HttpRunner自动化测试之响应中文乱码处理
响应中文乱码: 当调用接口,响应正文返回的中文是乱码时,一般是响应正文的编码格式不为 utf-8 导致,此时需要根据实际的编码格式处理 示例: 图1中 extract 提取title标题,output 输出 title 变量值&#x…...
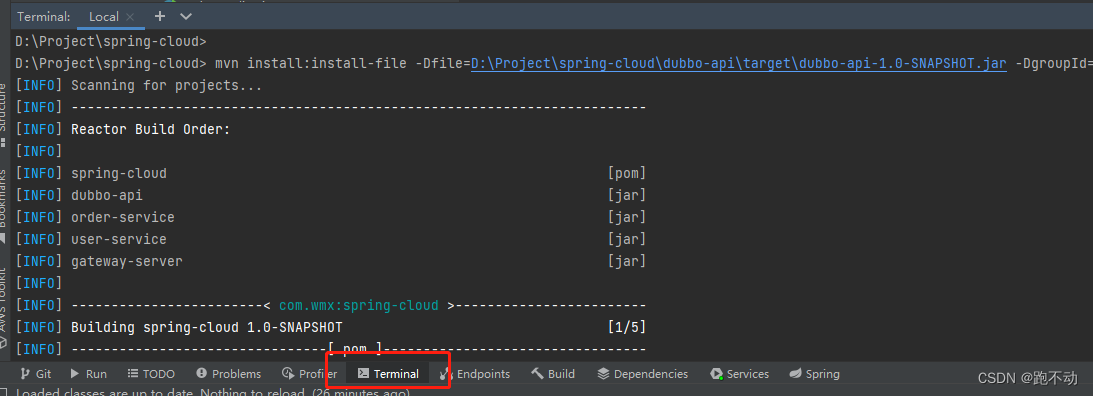
idea使用命令将jar包导入到maven仓库中
因为今天突然忘了命令,记下来方便以后查看 pom文件的依赖 jar包路径 进入idea中命令窗 输入命令 mvn install:install-file -DfileD:\Project\spring-cloud\dubbo-api\target\dubbo-api-1.0-SNAPSHOT.jar -DgroupIdcom.wmx -DartifactIddubbo-api -Dversion1.0…...
 Standalone模式(单机模式)安装)
zookeeper学习(一) Standalone模式(单机模式)安装
安装准备 centos7环境jdk1.8环境zookeeper安装包 安装jdk 上传jdk安装包解压安装包到目录中 tar -zxvf jdk-8u361-linux-x64.tar.gz如果需要指定目录可以在后面加上 -C,如 tar -zxvf jdk-8u361-linux-x64.tar.gz -C 目录配置jdk环境变量 vim /etc/profile打开…...

native webrtc支持切换音频采集设备和获取裸流
https://www.yuque.com/caokunchao/rtendq/oq8w3qgs3g59whru 前言 版本webrtc m96 1、修改webrtc m96代码,向外提供一个adm指针的接口出来 2、外部来获取指针进行设备的选择 3、外部获取音频裸流,麦克风或者扬声器的数据 修改webrtc代码 1、修改H:\w…...
HR怎么看待PMP证书呢?
在当今竞争激烈的职场环境中,拥有专业的证书已经成为了许多人提升职业竞争力的必要途径。PMP证书作为项目管理领域的国际认证,备受HR和企业的青睐。那么,HR在招聘和评估员工时,究竟是如何看待PMP证书的呢? 首先&#x…...

API接口:如何通过使用手机归属地查询
随着手机普及率的不断增加,手机号码的信息查询也成为了一个非常实用的功能。本文将介绍如何通过使用手机归属地查询API接口实现查询手机号码所在地的功能。 首先,我们需要一个可以查询手机号码所在地的API接口。目前市面上有很多免费或付费的API接口可供…...

小创业公司死亡剧本
感觉蛮真实的;很多小创业公司没有阿里华为的命,却得了阿里华为的病。小的创业公司要想活无非以下几点: 1 现金流,现金流,现金流; 2 产品,找痛点,不要搞伪需求; 3 根据公司…...
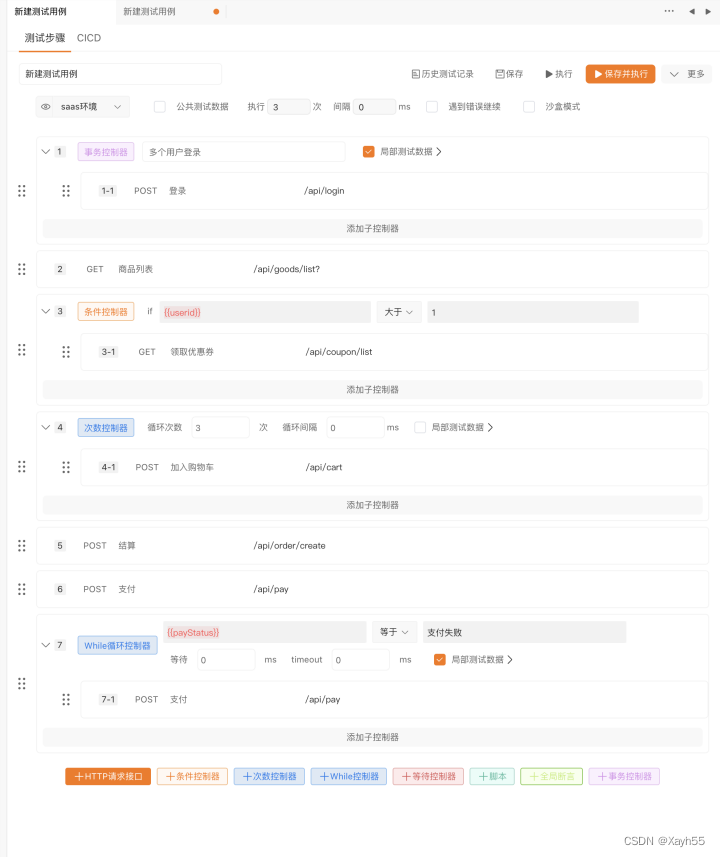
国产化的接口测试、接口自动化测试工具Apipost的介绍及使用
Apipost介绍: Apipost是 API 文档、API 调试、API Mock、API 自动化测试一体化的研发协作赋能平台,它的定位 Postman Swagger Mock JMeter。 Apipost 是接口管理、开发、测试全流程集成工具,能支撑整个研发技术团队同平台工作࿰…...
【MySQL】不允许你不知道如何插入数据
🎬 博客主页:博主链接 🎥 本文由 M malloc 原创,首发于 CSDN🙉 🎄 学习专栏推荐:LeetCode刷题集 🏅 欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正࿰…...
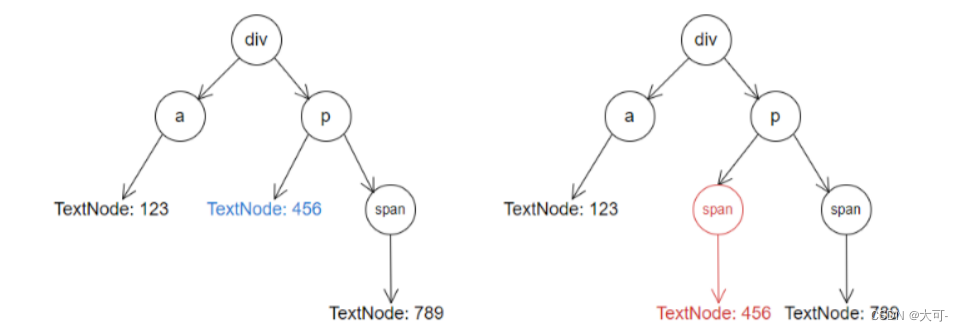
Vue 渲染流程详解
在 Vue 里渲染一块内容,会有以下步骤及流程: 第一步,解析语法,生成AST 第二步,根据AST结果,完成data数据初始化 第三步,根据AST结果和DATA数据绑定情况,生成虚拟DOM 第四步&…...
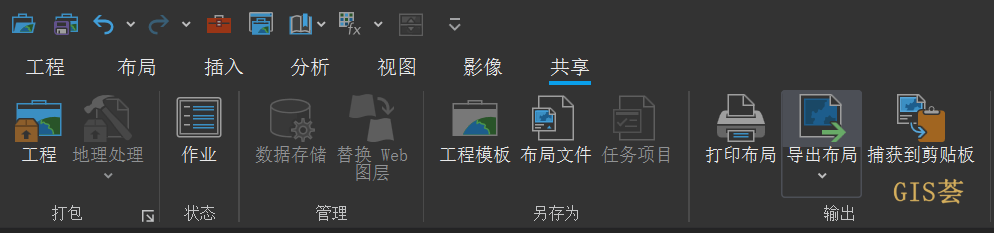
10分钟内入门 ArcGIS Pro
本文来源:GIS荟 大家好,这篇文章大概会花费你10分钟的时间,带你入门 ArcGIS Pro 的使用,不过前提是你有 ArcMap 使用经验。 我将从工程文件组织方式、软件界面、常用功能、编辑器、制图这5个维度给大家介绍。 演示使用的 ArcGI…...
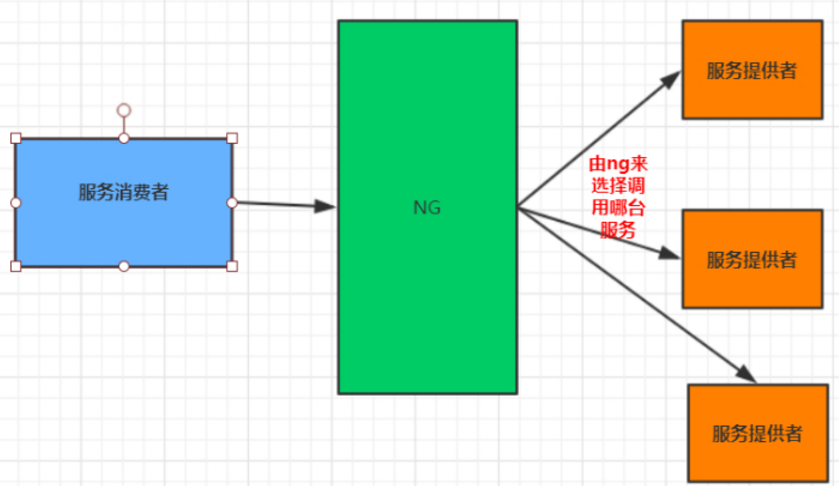
【ribbon】Ribbon的使用与原理
负载均衡介绍 负载均衡(Load Balance),其含义就是指将负载(工作任务)进行平衡、分摊到多个操作单元上进行运行,例如FTP服务器、Web服务器、企业核心应用服务器和其它主要任务服务器等,从而协同…...

axios封装到reques.js文件中
封装到js中,避免每次都import 然后写一大堆 import axios from axios /* 可复用的发 ajax 请求的函数: axios */ let baseURLhttp://localhost:3000/ export default function promiseAjax(url,methodget,datanull,params) {return new Promise((resolve, reject) …...

学好Elasticsearch系列-核心概念
本文已收录至Github,推荐阅读 👉 Java随想录 文章目录 节点角色master:候选节点data:数据节点Ingest:预处理节点ml:机器学习节点remote_ cluster_ client:候选客户端节点transform:…...

扩展点都不知道不要说你用了Spring Boot
文章目录 前言1.扩展点1.1. 应用程序生命周期扩展点1.1.1 SpringApplicationRunListener1.1.2 ApplicationEnvironmentPreparedEvent1.1.3 ApplicationPreparedEvent1.1.4 ApplicationStartedEvent1.1.5 ApplicationReadyEvent1.1.6 ApplicationFailedEvent 1.2. 容器扩展点1.2…...
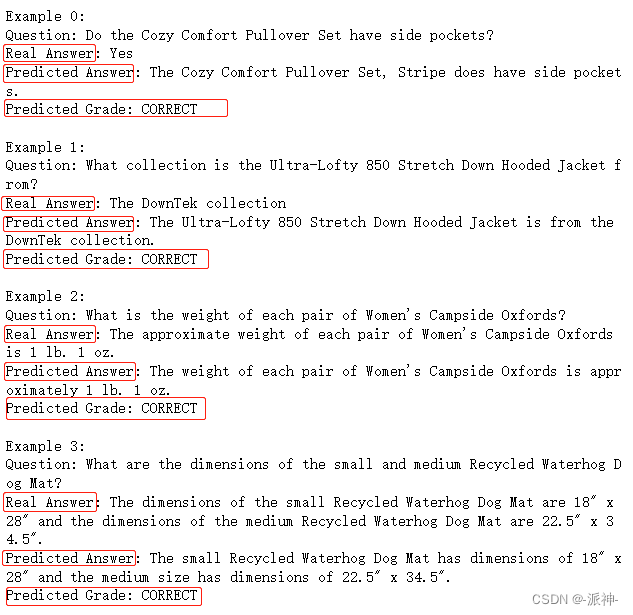
LangChain大型语言模型(LLM)应用开发(五):评估
LangChain是一个基于大语言模型(如ChatGPT)用于构建端到端语言模型应用的 Python 框架。它提供了一套工具、组件和接口,可简化创建由大型语言模型 (LLM) 和聊天模型提供支持的应用程序的过程。LangChain 可以轻松管理与语言模型的交互&#x…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...
