【C++】二叉搜索树的实现(递归和非递归实现)
文章目录
- 1、二叉搜索树
- 1.1 构建二叉搜索树
- 1.2 二叉搜索树的插入
- 1.3 二叉搜索树的删除
- 1.4 二叉搜索树插入和删除的递归实现
为了学习map和set的底层实现,需要知道红黑树,知道红黑树之前需要知道AVL树。
红黑树和AVL树都用到了二叉搜索树结构,所以先谈谈二叉搜索树。
1、二叉搜索树
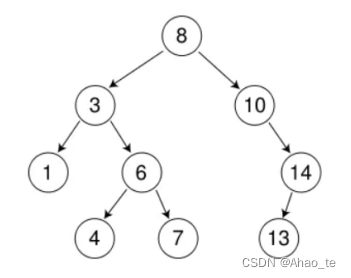
二叉搜索树(Binary Search Tree)也称二叉排序树,它最重要的是能给数据排序以及去重。
其性质:
- 若左子树不为空,左子树的键值都小于根以及右子树。
- 若右子树不为空,右子树的键值都大于根以及左子树。
- 二叉搜索树的子树都是二叉搜索树。
二叉搜索树顾名思义,根据其特性可以很方便让我们搜索一个值。
二叉树的中序遍历就是一个排序。
二叉搜索树的结点没有相同的值。
值得注意的是:
- 二叉搜索树没有要求严格平衡,所以查找一个值的时间复杂度最坏可能是O(N)(成为单枝树,就是一个链表。)
- 二叉搜索树不支持值修改,因为会打乱树的结构。
1.1 构建二叉搜索树
在二叉树的模型中,有K模型和KV模型,就是一个结点一个值和一个结点一个键值对两个模型。
一个值的很简单,而KV模型就是一个结点存放一个key和一个value。
下面实现的是KV模型的基本框架
#include <iostream>
#include <assert.h>
#include <string>
using namespace std;template<class K, class V>
struct BSTreeNode
{//设置成三叉链的结构,让子树能方便访问根结点struct BSTreeNode<K, V>* _left;struct BSTreeNode<K, V>* _right;struct BSTreeNode<K, V>* _parent;K _key;V _value;//构造BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _parent(nullptr), _key(key), _value(value){}
};template<class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;
public:
private:Node* _root = nullptr;
};
1.2 二叉搜索树的插入
二叉树插入很简单。
1、如果树是空,直接创建结点返回。
2、树不为空,根据搜索树的特性通过值的大小确定应该放在左还是右子树,如果到达空结点,那么就到达该放的位置。
3、确认好放的位置,因为需要链接,所以需要有一个parent能指向上一个结点。通过上一个结点和新结点的大小判断应该链接在哪边。
4、因为设计的是三叉链结构,所以最后还得指向父节点。
bool Insert(const K& key, const V& value){ //树为空if (_root == nullptr){_root = new Node(key, value);return true;}Node* cur = _root;Node* parent = _root;//找到新结点应该放的位置while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{//如果值相同直接返回return false;}}//确认好位置后,父子结点互相链接cur = new Node(key, value);if (parent->_key < cur->_key){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}return true;}
1.3 二叉搜索树的删除


bool Erase(const K& key){//空树返回if (_root == nullptr){return false;}Node* cur = _root;Node* parent = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{//先找到需要删的结点//删的结点左为空if (cur->_left == nullptr){//删的结点为根节点情况if (parent == cur){_root = cur->_right;}else{//需要确定父节点哪边指向curif (parent->_right == cur){parent->_right = cur->_right;}else{parent->_left = cur->_right;}}delete cur;}else if (cur->_right == nullptr){//删的结点右为空//删的结点为根节点情况if (parent == cur){_root = cur->_left;}else{if (parent->_right == cur){parent->_right = cur->_left;}else{parent->_left = cur->_left;}}delete cur;}else{//左右都不为空,替换右子树最小的Node* minRight = cur->_right;while (minRight->_left){minRight = minRight->_left;}cur->_key = minRight->_key;cur->_value = minRight->_value;parent = minRight->_parent;//需要确定父节点哪边指向minRightif (parent->_right == minRight){parent->_right = minRight->_right;}else{parent->_left = minRight->_right;}//因为值交换了,所以删除右子树最小结点delete minRight;} //elsereturn true;} //else} // whilereturn false;} //Erase
1.4 二叉搜索树插入和删除的递归实现
有一点必须明确的是,非递归一定是比递归要好的,这里实现递归只是练习,增强代码能力。
首先是InOrder()方法的实现,当调用的方法是不含参数的,实现又需要有参数的,就可以再嵌套一层,并且_InOrder(Node* root)不想提供给类外调用,就可以放在私有域。
...
template<class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;
public:bool Insert(const K& key, const V& value){}bool Erase(const K& key){}void InOrder(){_InOrder(_root);}
private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}Node* _root = nullptr;
};
插入的递归实现
插入递归很简单,值得说的是,通过给root添加引用,能很方便的将新结点链接起来。
...
template<class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;
public:...bool Insert(const K& key, const V& value){return _InsertR(_root, key, value);}bool Erase(const K& key){}...
private:...bool _InsertR(Node*& root, const K& key, const V& value){if (root == nullptr){//因为需要对root修改,所以在参数部分需要对root添加引用(Node*& root)root = new Node(key, value);return true;}if (root->_key < key){_InsertR(root->_right, key, value);}else if (root->_key > key){_InsertR(root->_left, key, value);}else{return false;}}Node* _root = nullptr;
};
删除的递归实现
删除的思路整体上和非递归差不多,不同的是。
1、因为删除需要改变树的结构,肯定是要改变每次递归的根节点的,所以需要传引用。
2、删除的思路是和右子树最小结点值交换后,删除最小结点。需要往右找到最小结点。
...
template<class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;
public:bool Erase(const K& key){_EraseR(_root, key);}
private:
...bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return _EraseR(root->_right, key);}else if(root->_key > key){return _EraseR(root->_left, key);}else{//找到删除的结点Node* del = root;if (root->_left == nullptr){//左边为空//因为要改变树的结构,改变root,所以root得加&//引用加完后,改变root也代表着改变父结点的指向//所以就是父节点指向root的指向变成指向root的右子树root = root->_right;}else if (root->_right == nullptr){//右边为空root = root->_left;}else{Node* minRight = root->_right;while (minRight->_left){minRight = minRight->_left;}swap(root->_key, minRight->_key);// 转换成子树中去删除节点// 因为和最小节点的值交换后,原本root的值成了最小值// 再凭借key去查找最小值的结点删// 最小节点左边一定为空_EraseR(root->_right, key);}delete del;return true;} //else}Node* _root = nullptr;
};
本章完~
相关文章:

【C++】二叉搜索树的实现(递归和非递归实现)
文章目录1、二叉搜索树1.1 构建二叉搜索树1.2 二叉搜索树的插入1.3 二叉搜索树的删除1.4 二叉搜索树插入和删除的递归实现为了学习map和set的底层实现,需要知道红黑树,知道红黑树之前需要知道AVL树。 红黑树和AVL树都用到了二叉搜索树结构,所…...

春招来了,如何正确使用领英超高效招聘海外员工、挖掘人才?
金三银四到了,每年的这个时候都是企业招聘的好时机。而领英是目前全球最大的职场社交网络平台,基本上海外求职都是在使用它,所以很多企业涉及到海外招聘时,都会优先考虑领英,但是却经常缺乏一些经验技巧,今…...

Mysql中锁机制深入理解
Mysql中锁机制深入理解默认大家已经知道。分类性能悲观锁,乐观锁操作类型读锁,写锁,数据粒度表锁,行锁,页面锁更细粒度间隙锁,临键锁按使用来讲。由数据粒度出发。表锁,分为 共享锁,…...

去中心化社交网络协议除了Nostr还有哪些?
当下最火的去中心化社交软件Dmaus就是基于Nostr协议开发的,Nostr协议的基本情况之前的文章《一文了解去中心化社交网络协议Nostr》已经做了详细介绍,本文将介绍其他几个目前比较流行的去中心化社交协议。FarcasterFarcaster是由前Coinbase高管Dan Romero…...

【FT2000/4+X100】调试记录
订阅专栏 硬件环境FT2000/4+X100,单板结构,对外显示,运行银行麒麟操作系统。 一 生成UEFI.BIN,烧写在FT2000-4的QSPI Flash中 1 2 下载源文件 edk2-for-support.tar; 参考文件 ft2004c&D2000编译打包说明V1.0.5; 解压源文件; 根目录下 build2004C.sh为四核产品…...
我的Android启动优化—【黑白屏优化】
简述 在Android App使用过程中,对于应用的优化是一个加分项,举个例子,打开你的App需要2秒,人家0.5秒,这就是很大的用户体验上的优化。 问题的产生 在开发中,我们在启动app的时候,屏幕会出现一…...

TongWeb8编码设置说明
应用场景:在遇到中文问题时,常需要通过设置编码格式来解决问题。下面介绍TongWeb8的编码设置及优先级。一、web.xml中请求、响应编码的配置优先级最高在JavaEE8规范中web.xml增加了request, response编码配置,该配置优先级最高。<?xml ve…...

不同相机之间图片像素对应关系求解(单应性矩阵求解)
一、场景 相机1和相机2相对位置不变,相机拍摄图片有重叠,求他们交叠部分的一一对应关系。数学语言描述为已知相机1图片中P点像素(u1, v1),相机1中P点在相机2图片中像素值为(u2, v2),它们存在某种变换,求变换矩阵。 因为…...

远程管理时代,还得是智能化PDU才靠得住!
在如今这个信息技术高速发展的时代,数据中心IDC机房服务器数量与日俱增,提供DNS域名服务、主机托管服务、虚拟主机服务等服务的服务器是IDC最基本的功能之一。服务器需要7*24小时不间断持续工作,但当服务器数量很大,服务器工作、重…...
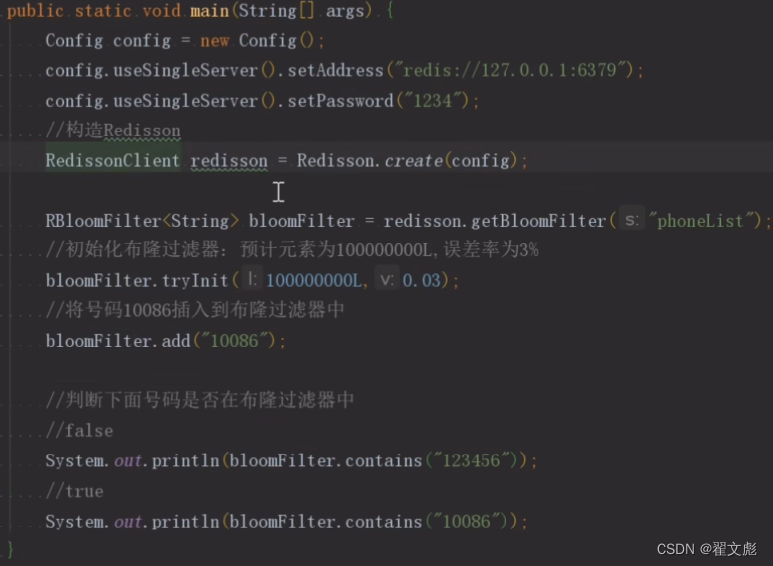
通俗易懂理解——布隆过滤器
文章目录概述本质优缺点优点:缺点:实际应用解决redis缓存穿透问题:概述 本质 本质:很长的二进制向量(数组) 主要作用:判断一个数据在这个数组中是否存在,如果不存在为0,…...

TypeScript 学习之类型推导
在一些情况下,代码上没有显性明确类型,typescript 可以隐形推断出类型。 基础 let x 3;变量x的类型被推断为数字。 类型推断发生在初始化变量和成员,设置默认参数值和决定函数返回值时 最佳通用类型 let x [0, 1, null]; // 类型为 numb…...

Android四大组件——Service详解
Service 为后台运行,不可见,没有界面。优先级高于Activity(内存不足时先杀掉Activity),运行在主线程且不能做耗时操作。 一、Service 启动方式 1、startService() 通过 startService 启动后,service会一直…...

svg转png
svg转png写了一个spring boot项目,支持传入svg文件转出png图片,并且自定义转出png的宽和高。主要代码如下:所需依赖如下:演示如下:首先,运行项目使用接口调用工具调用接口发送请求,提取文件1000…...

教你如何搭建人事OA-员工管理系统,demo可分享
1、简介1.1、案例简介本文将介绍,如何搭建人事OA-员工管理。1.2、应用场景人事OA-员工管理应用对员工信息进行管理,可办理入职、转正、离职等流程。2、设置方法2.1、表单搭建1)新建表单【员工管理】,字段设置如下:名称…...

C++递推基础知识
文章目录一、递推的概念二、递推和递归的区别三、递推的实例1、最基础的:斐波那契数列2、变形版斐波那契数列3、较复杂的递推式求解:昆虫繁殖4、经典逆推问题:题目数量一、递推的概念 1、什么是递推算法? 递推算法:是…...

【Python入门第十天】Python 布尔
布尔表示两值之一:True 或 False。 布尔值 在编程中,通常需要知道表达式是 True 还是 False。 可以计算 Python 中的任何表达式,并获得两个答案之一,即 True 或 False。 比较两个值时,将对表达式求值,P…...
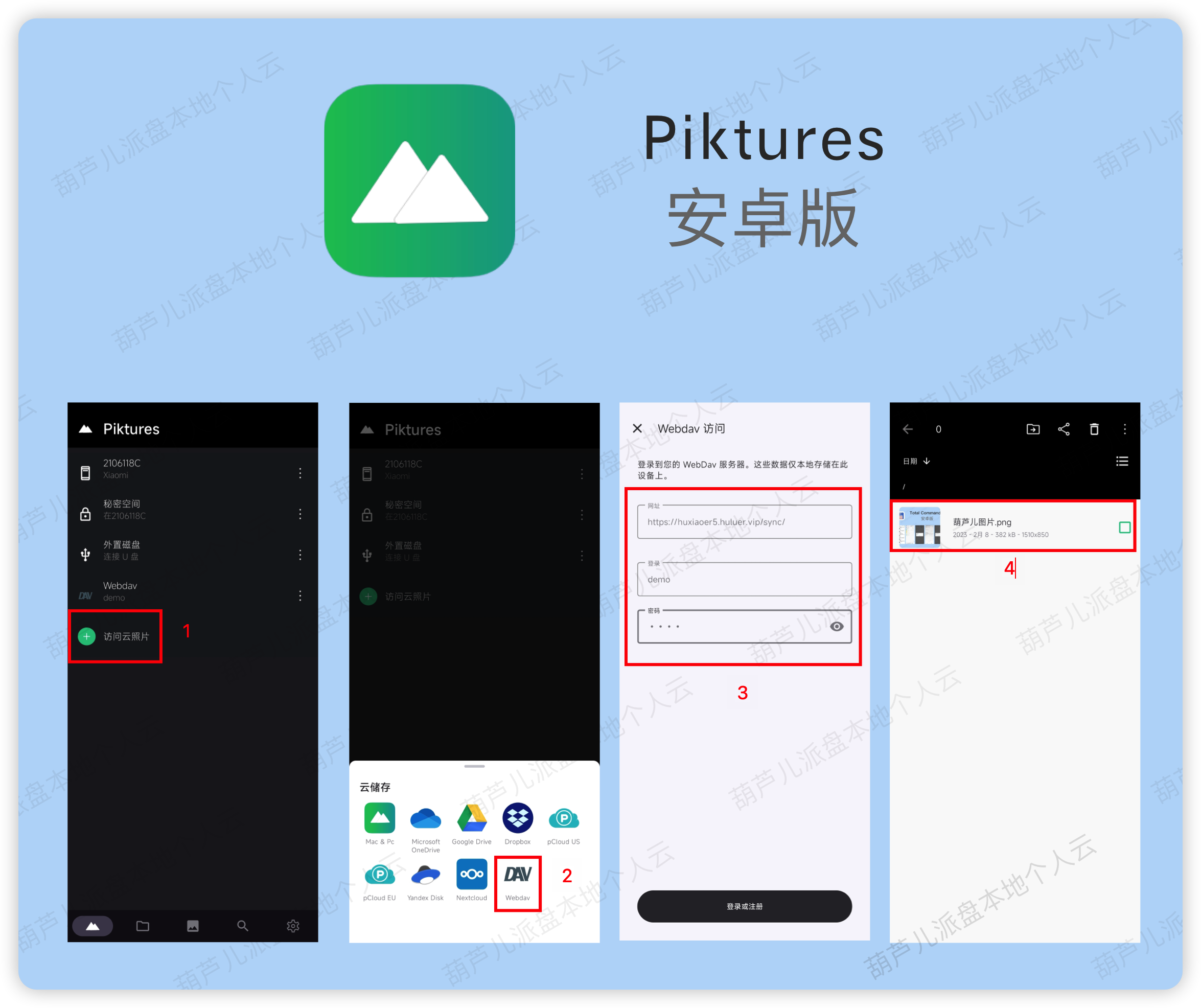
WebDAV之π-Disk派盘+Piktures
Piktures支持WebDAV方式连接π-Disk派盘。推荐一款简单易用,功能超级强大的智能相册应用。Piktures智能相册是一款简单易用,功能超级强大的智能相册应用,它不仅可以访问本地和云照片,还可以照片编辑器,而且它同时还是一…...
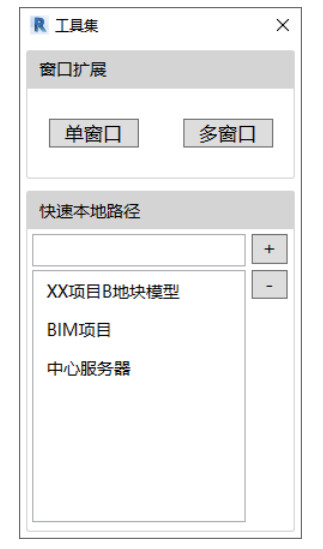
Revit问题:Navisworks中导入的rvt模型角度不正确调整
一、Navisworks中导入的rvt模型角度不正确调整方法 通常情况下,我们做好一个Revit模型,有时候出于成果保护或者鉴于Revit自带的碰撞检测效果不够直观、Revit模型体量太大,需要一个轻量化的模型展示,我们通常情况下会使用Autodesk公…...

最全正则验证
一、校验数字的表达式 1. 数字:^[0-9]*$ 2. n位的数字:^\d{n}$ 3. 至少n位的数字:^\d{n,}$ 4. m-n位的数字:^\d{m,n}$ 5. 零和非零开头的数字:^(0|[1-9][0-9]*)$ 6. 非零开头的最多带两位小数的数字:…...
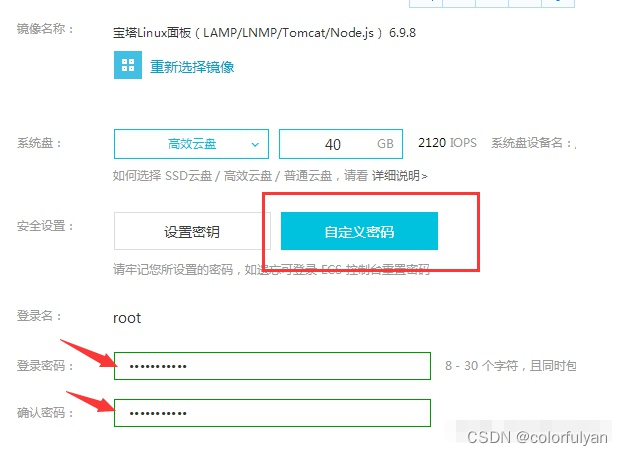
阿里云服务器入门使用流程 新手学习教程
一、阿里云根据个人需要选合适的云服务器,选好cpu、内存、带宽,地域,这四个是主要的。其他可以默认选择。 二、登陆控制台 输入账号密码,进去看到服务界面,新手可能不容易看懂。点击左侧菜单,点击云服务器…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
