不同相机之间图片像素对应关系求解(单应性矩阵求解)
一、场景
相机1和相机2相对位置不变,相机拍摄图片有重叠,求他们交叠部分的一一对应关系。数学语言描述为已知相机1图片中P点像素(u1, v1),相机1中P点在相机2图片中像素值为(u2, v2),它们存在某种变换,求变换矩阵。
因为涉及的场景比较简单,目前没有涉及深度,同时采集的目标近似平面,所以可以简化场景,采用单应性矩阵求解。所以上述所涉及的变换矩阵假设为单应性矩阵H(3*3矩阵),它们满足如下关系。

这样的话,简单很多(如果场景复杂,涉及了深度或者采集对象不是平面,可以使用本质矩阵/基础矩阵的方法获取这个变换矩阵),只需借助标准标定板计算得到H。
二、单应性矩阵
定义:用 [理想成像] 的相机从不同位置拍摄 [同一平面物体] 的图像之间存在单应性,可以用 [透视变换] 表示 。有以下公式:

接下来就是求解H矩阵,上述公式展开如下:

由平面坐标与齐次坐标对应关系,上式可以表示为:
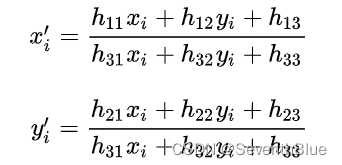
进一步,
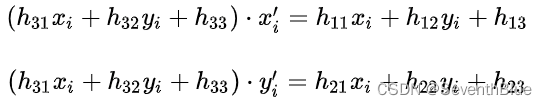
写成AX=0形式,如下。这种形式求解方式很多,前面的博客也有所涉及。不过需要特别指出的是,虽然H矩阵有9个未知数,但是只有8个自由度(平面关系),其中h33=1。所以求解方程只需要4个不共线点即可求解。

三、实际效果
3.1 全部代码
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import cv2
import numpy as npdef OnMouseAction(event, x, y, flags, param):"""鼠标的回调函数,处理鼠标事件:param event::param x::param y::param flags::param param::return:"""if event == cv2.EVENT_LBUTTONDOWN:global gimg_x, gimg_y, gis_okgimg_x = xgimg_y = ygis_ok = Trueelif event == cv2.EVENT_RBUTTONDOWN:print("右键点击")elif flags == cv2.EVENT_FLAG_LBUTTON:print("左鍵拖曳")elif event == cv2.EVENT_MBUTTONDOWN:print("中键点击")def verification(img1, img2, H):def nothing(x):passcv2.namedWindow('image1')cv2.setMouseCallback('image1', OnMouseAction)# create trackbars for color changecv2.createTrackbar('thr', 'image1', 121, 255, nothing)cv2.createTrackbar('Shading', 'image1', 255, 255, nothing)count = 0while True:cv2.imshow("image1", img1)cv2.imshow("image2", img2)k = cv2.waitKey(1) & 0xFF# 通过关闭窗口的右上角关闭if cv2.getWindowProperty('image1', cv2.WND_PROP_AUTOSIZE) < 1:break# 通过按键盘的ESC退出if k == 27:breakglobal gimg_x, gimg_y, gis_okif gis_ok:count += 1cv2.circle(img1, (gimg_x, gimg_y), 3, (0, 0, 255), -1)cv2.putText(img1, str(count), (gimg_x, gimg_y), 2, 1, (0, 0, 255))gis_ok = False(x, y, z) = np.matmul(H, np.array([gimg_x, gimg_y, 1]).T)cv2.circle(img2, (int(x / z), int(y / z)), 2, (0, 0, 255), -1)cv2.putText(img2, str(count), (int(x / z), int(y / z)), 2, 1, (0, 0, 255))def getHomography(img1, img2):gray1 = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)gray2 = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)ret, corners1_1 = cv2.findChessboardCorners(gray1, (gcols, grows), None)if not ret:return ret, None# sub-pixel corner detectioncorners1_2 = cv2.cornerSubPix(gray1, corners1_1, (11, 11), (-1, -1), criteria)ret, corners2_1 = cv2.findChessboardCorners(gray2, (gcols, grows), None)if not ret:return ret, None# sub-pixel corner detectioncorners2_2 = cv2.cornerSubPix(gray2, corners2_1, (11, 11), (-1, -1), criteria)H, mask = cv2.findHomography(corners1_2, corners2_2, cv2.RANSAC)return True, Hgimg1Root = "./image_homography/1080p_1.png"
gimg2Root = "./image_homography/1080p_2.png"
gimg3Root = "./image_homography/720p_3.png"
(grows, gcols) = (8, 11)
def main():img1 = cv2.imread(gimg1Root)img2 = cv2.imread(gimg3Root)is_ok, H = getHomography(img1, img2)print(H)verification(img1, img2, H)global gimg_x, gimg_y, gis_ok
gimg_x = 0
gimg_y = 0
gis_ok = False
if __name__ == "__main__":main()3.2 实际效果

相关文章:

不同相机之间图片像素对应关系求解(单应性矩阵求解)
一、场景 相机1和相机2相对位置不变,相机拍摄图片有重叠,求他们交叠部分的一一对应关系。数学语言描述为已知相机1图片中P点像素(u1, v1),相机1中P点在相机2图片中像素值为(u2, v2),它们存在某种变换,求变换矩阵。 因为…...

远程管理时代,还得是智能化PDU才靠得住!
在如今这个信息技术高速发展的时代,数据中心IDC机房服务器数量与日俱增,提供DNS域名服务、主机托管服务、虚拟主机服务等服务的服务器是IDC最基本的功能之一。服务器需要7*24小时不间断持续工作,但当服务器数量很大,服务器工作、重…...
通俗易懂理解——布隆过滤器
文章目录概述本质优缺点优点:缺点:实际应用解决redis缓存穿透问题:概述 本质 本质:很长的二进制向量(数组) 主要作用:判断一个数据在这个数组中是否存在,如果不存在为0,…...

TypeScript 学习之类型推导
在一些情况下,代码上没有显性明确类型,typescript 可以隐形推断出类型。 基础 let x 3;变量x的类型被推断为数字。 类型推断发生在初始化变量和成员,设置默认参数值和决定函数返回值时 最佳通用类型 let x [0, 1, null]; // 类型为 numb…...

Android四大组件——Service详解
Service 为后台运行,不可见,没有界面。优先级高于Activity(内存不足时先杀掉Activity),运行在主线程且不能做耗时操作。 一、Service 启动方式 1、startService() 通过 startService 启动后,service会一直…...

svg转png
svg转png写了一个spring boot项目,支持传入svg文件转出png图片,并且自定义转出png的宽和高。主要代码如下:所需依赖如下:演示如下:首先,运行项目使用接口调用工具调用接口发送请求,提取文件1000…...

教你如何搭建人事OA-员工管理系统,demo可分享
1、简介1.1、案例简介本文将介绍,如何搭建人事OA-员工管理。1.2、应用场景人事OA-员工管理应用对员工信息进行管理,可办理入职、转正、离职等流程。2、设置方法2.1、表单搭建1)新建表单【员工管理】,字段设置如下:名称…...

C++递推基础知识
文章目录一、递推的概念二、递推和递归的区别三、递推的实例1、最基础的:斐波那契数列2、变形版斐波那契数列3、较复杂的递推式求解:昆虫繁殖4、经典逆推问题:题目数量一、递推的概念 1、什么是递推算法? 递推算法:是…...

【Python入门第十天】Python 布尔
布尔表示两值之一:True 或 False。 布尔值 在编程中,通常需要知道表达式是 True 还是 False。 可以计算 Python 中的任何表达式,并获得两个答案之一,即 True 或 False。 比较两个值时,将对表达式求值,P…...
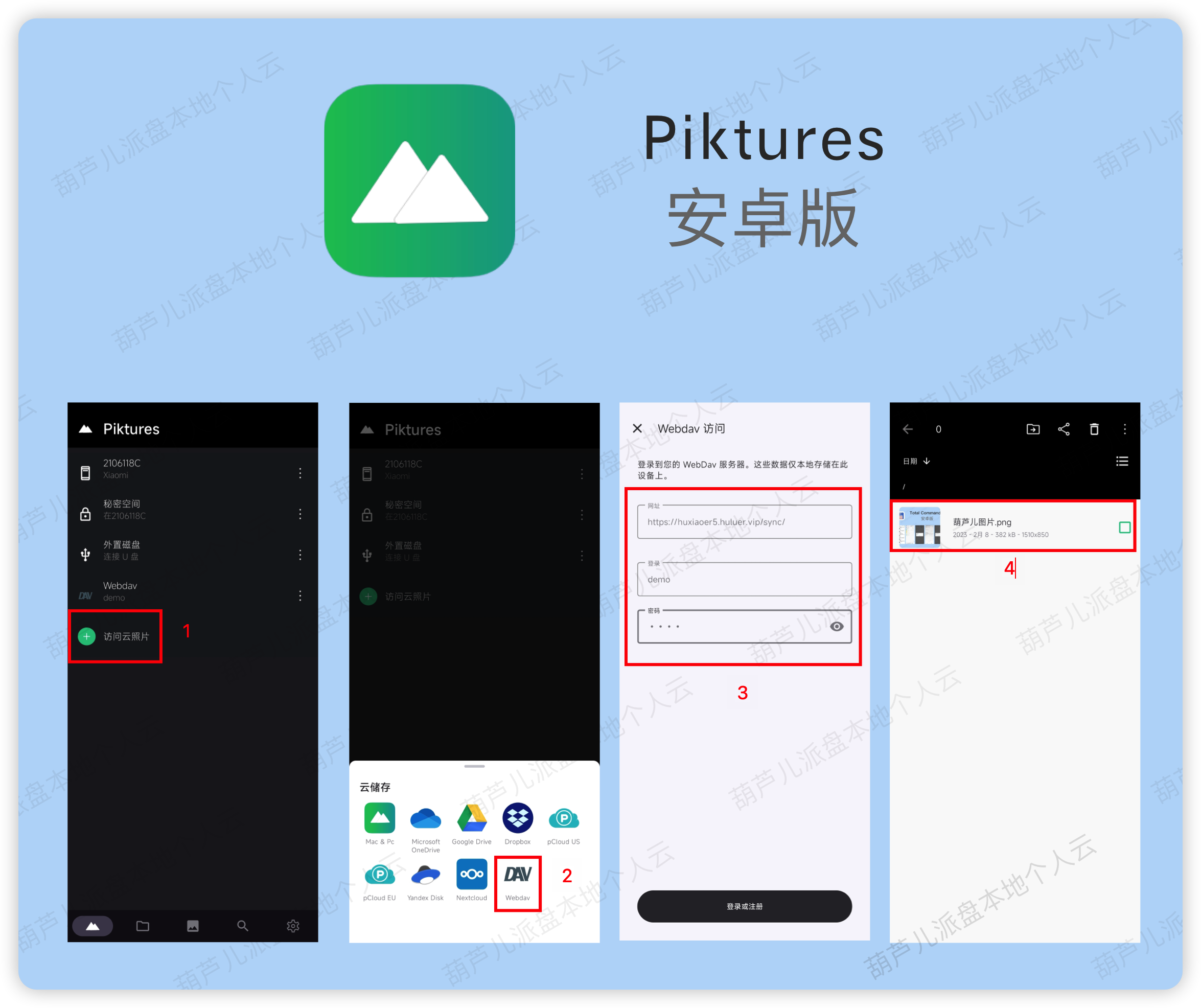
WebDAV之π-Disk派盘+Piktures
Piktures支持WebDAV方式连接π-Disk派盘。推荐一款简单易用,功能超级强大的智能相册应用。Piktures智能相册是一款简单易用,功能超级强大的智能相册应用,它不仅可以访问本地和云照片,还可以照片编辑器,而且它同时还是一…...
Revit问题:Navisworks中导入的rvt模型角度不正确调整
一、Navisworks中导入的rvt模型角度不正确调整方法 通常情况下,我们做好一个Revit模型,有时候出于成果保护或者鉴于Revit自带的碰撞检测效果不够直观、Revit模型体量太大,需要一个轻量化的模型展示,我们通常情况下会使用Autodesk公…...

最全正则验证
一、校验数字的表达式 1. 数字:^[0-9]*$ 2. n位的数字:^\d{n}$ 3. 至少n位的数字:^\d{n,}$ 4. m-n位的数字:^\d{m,n}$ 5. 零和非零开头的数字:^(0|[1-9][0-9]*)$ 6. 非零开头的最多带两位小数的数字:…...
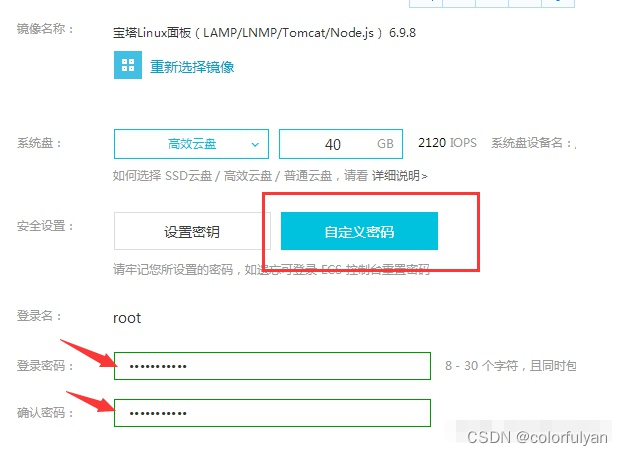
阿里云服务器入门使用流程 新手学习教程
一、阿里云根据个人需要选合适的云服务器,选好cpu、内存、带宽,地域,这四个是主要的。其他可以默认选择。 二、登陆控制台 输入账号密码,进去看到服务界面,新手可能不容易看懂。点击左侧菜单,点击云服务器…...

git学习
一.实际场景 数据备份代码还原协同开发追溯问题代码的编写人和编写时间 二.Git工作流程图 三.获取本地仓库 四.git add和git commit git status:查看修改的状态(暂存区,工作区) git add . :通配符,添加当…...
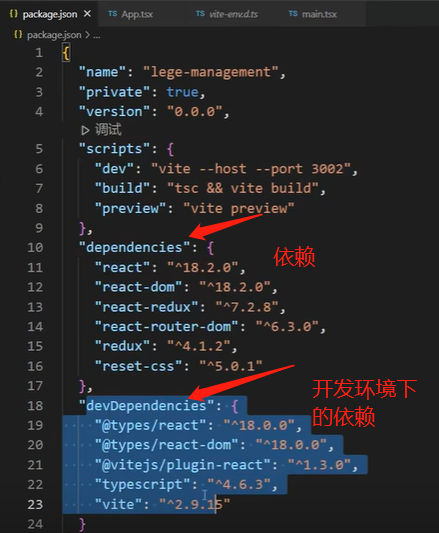
新建一个完整的react项目和完善初始项目
一:新建一个完整的react项目 1.环境准备 目前我的环境是 node:16.17.1 npm: 8.15.0 查看环境:1):打开命令提示符工具,利用node -v和npm -v 查看一下自己的环境,如果觉得重新卸载、安装node比较…...
HIVE 安装
目录 启动hadoop 把hive压缩包拷贝到虚拟机里面 解压 改名 配置环境变量 新建一个hive-site.xml文件,并编辑 配置文件 添加jar包 初始化mysql 启动hive 创建数据库 使用数据库 创建表 添加数据 查看数据 删除表 安装虚拟机 安装JDK 安装Hadoop …...
jsp游泳馆门票管理系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 jsp游泳馆门票管理系统 是一套完善的web设计系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为 TOMCAT7.0,Myeclipse8.5开发,数据库为Mysql,…...
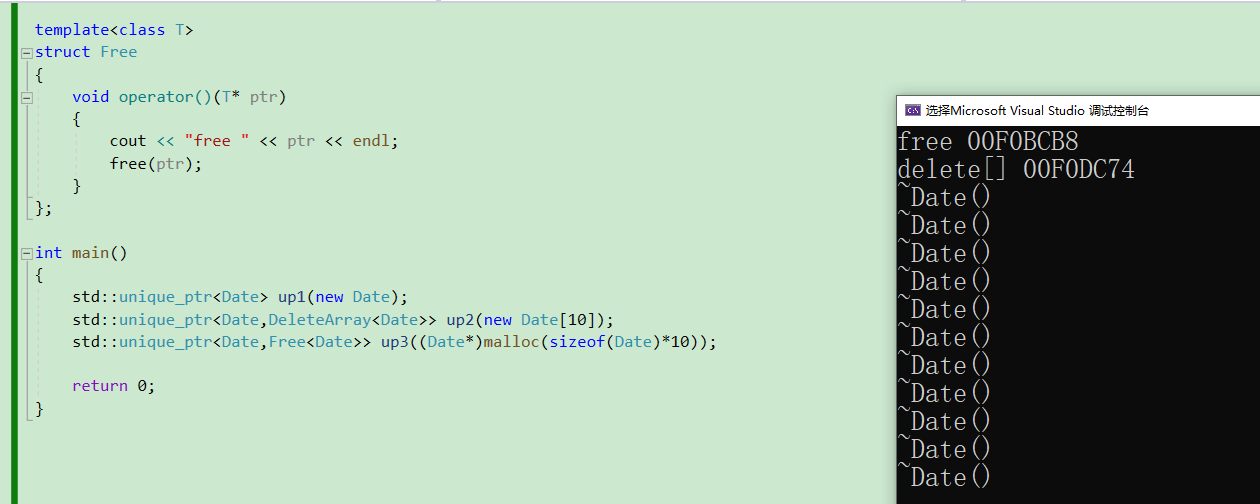
C++ ---智能指针详解
文章目录前言一、 为什么需要智能指针?二、内存泄漏2.1 什么是内存泄露?危害是什么?2.2 内存泄露的分类2.3 如何避免内存泄露三、智能指针的使用及原理3.1 RAII3.2 智能指针的原理3.3 std::autoptr3.4 std::unique_ptr3.5 std::shared_ptrstd::shared_ptr的循环引…...

企业带宽控制管理
在企业中保持稳定的网络性能可能具有挑战性,因为采用数字化的网络可扩展性和敏捷性应该与组织的发展同步。随着基础设施的扩展、新应用和新技术的引入,网络的带宽容量也在增加。 停机和带宽过度使用是任何组织都无法避免的两个问题,为了解决…...
MybatisPlus实现分页效果并解决错误:cant found IPage for args!
前言 早就知道MybatisPlus对分页进行了处理,但是一直没有实战用过,用的是自己封装的一个分页组件,虽不说麻烦吧,但是也不是特别简单。 写起来还是比较复杂,但是最近这个组件有了点小小的bug,我决定是时候…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...
