【LeetCode】55.跳跃游戏
题目
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
示例 1:
输入:nums = [2,3,1,1,4] 输出:true 解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4] 输出:false 解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
提示:
1 <= nums.length <= 3 * 10^40 <= nums[i] <= 10^5
解答
源代码
class Solution {public boolean canJump(int[] nums) {// k表示最远能够走到哪个下标int k = 0;// i代表现在走到哪个下标for (int i = 0; i < nums.length; i++) {if (i > k) {return false;}k = Math.max(k, i + nums[i]);}return true;}
}总结
这个题不用想得太复杂,就直接把遍历数组想象成走路,计算出当前可到达的最远下标,在向前走时不断对比更新可到达的最远下标,若当前走到的下标已经大于可到达的最远下标,那就表示这个数组没办法到达最后一个下标。
相关文章:

【LeetCode】55.跳跃游戏
题目 给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。 数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标。 示例 1: 输入:nums [2,3,1,1,4] 输出:true 解释:可以…...

Docker学习路线12:开发者体验
到目前为止,我们只讨论了使用Docker来部署应用程序。然而,Docker也是一个极好的用于开发应用程序的工具。可以采用一些不同的建议来改善开发体验。 在应用程序中使用docker-compose以方便开发。使用绑定挂载将本地代码挂载到容器文件系统中,…...

后端服务迁移方案及过程记录
阶段时序动作双写数据对比1新rdb集群上线双写数据对比2新服务上线,无流量双写数据对比2后端自己发起的流程比如job,新服务上线一份新的,独立运行双写数据对比2消费二方mq,新服务使用新的消费组消费原有消息双写数据对比3新旧服务比…...

StAX解析
StAX解析 StAX解析介绍 StAX解析与SAX解析类似,也是基于事件驱动的,不同之处在于StAX采用的是拉模式,应用程序通过调用解析器推进解析的进程,可以调用next()方法来获取下一个解析事件(开始文档,结束文档,开…...

[MCU]AUTOSAR COM STACK - CAN协议栈
各层PDU PDU:Protocal Data Unit,协议数据单元,由SDU和PCI组成; I-PDU:Interaction Layer PDU,数据交互层PDU;N-PDU:NetWork Layer PDU,网络层PDU,通常用的…...

React:从 npx开始
使用 npm 来创建第一个 recat 文件( react-demo 是文件名,可以自定义) npx create-react-app react-demo npx是 npm v5.2 版本新添加的命令,用来简化 npm 中工具包的使用 原始: 全局安装npm i -g create-react-app 2 …...
力扣热门100题之接雨水【困难】
题目描述 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3…...

Stable-Diffusion-Webui部署SDXL0.9报错参数shape不匹配解决
问题 已经在model/stable-diffusion文件夹下放进去了sdxl0.9的safetensor文件,但是在切换model的时候,会报错model的shape不一致。 解决方法 git pullupdate一些web-ui项目就可以,因为当前项目太老了,没有使用最新的版本。...

Springboot @Async 多线程获取返回值
Springboot Async 多线程获取返回值 需求背景 最近需要用到多线程, 自己维护线程池很麻烦, 正好看到Springboot集成线程池的例子, 这里自己做了个尝试和总结, 记录一下, 也分享给需要的朋友; 不考虑事务的情况下, 这个多线程实现比较简单, 主要有以下几点: 在启动类加上Enab…...

怎样接入chatGPT
官网链接: OpenAI platform...
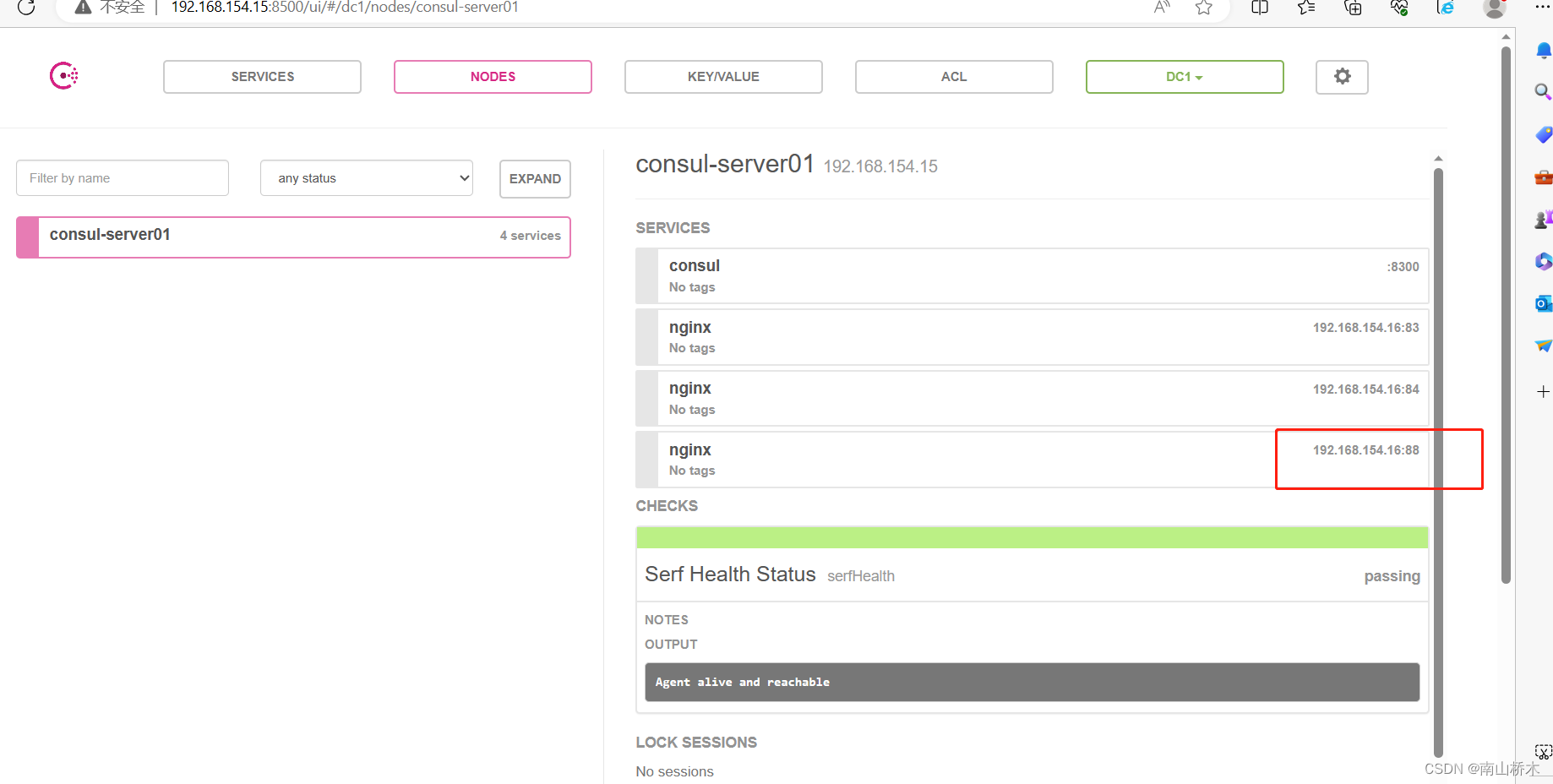
Docker consul容器服务更新与发现
Docker consul容器服务更新与发现 一、什么事服务注册与发现二、什么是consul三、consul部署1、consul服务器2、registrator服务器3、consul-template 一、什么事服务注册与发现 服务注册与发现是微服务架构中不可或缺的重要组件。起初服务都是单节点的,不保障高可…...

[算法很美打卡] 多维数组篇 (打卡第一天)
文章目录 顺时针打印二维数组0所在的行列清零 顺时针打印二维数组 package 每日算法学习打卡.算法打卡.七月份.七月二十六号;public class test1 {public static void main(String[] args) {int[][] matrix {{1,2},{5,6},{9,10},{13,14},};print(matrix);}static void print(i…...
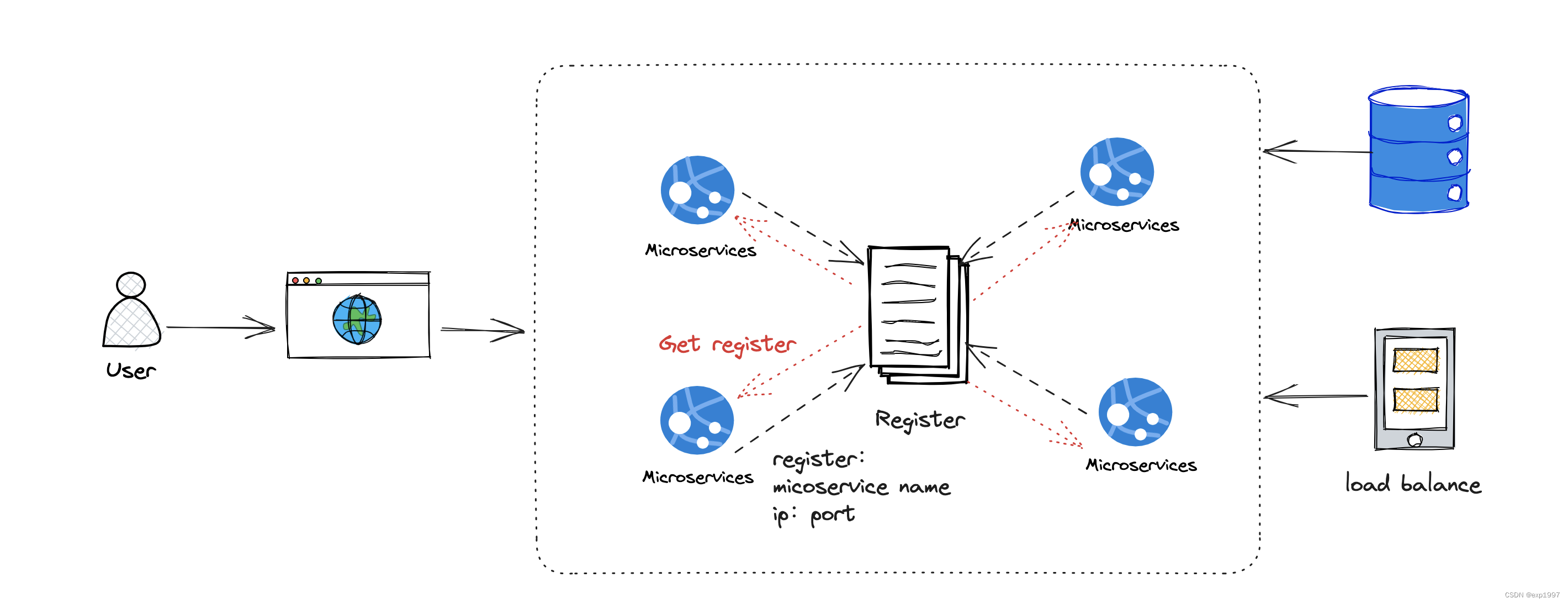
微服务系列(1)-who i am?
微服务系列(1)-我是谁 应用架构的演化 简单来说系统架构可以分为以下几个阶段:复杂的臃肿的单体架构-SOA架构-微服务 单体架构及其所面临的问题 在互联网发展初期,用户数量少,流量小,硬件成本高。因此…...

记录这这段时间发生的事情。
当做后端的时候总是被骂做前很丑。成为一个UI设计师与后端工程师才会更加完美。 尝试着做一个主页面。 创建了一个主页面 的表格index。 收录了希望发送到主页的,的帖子。 并且,可以填写是否可以。 一个看起来不错的主页。 标题设计的左右框。 这种框…...
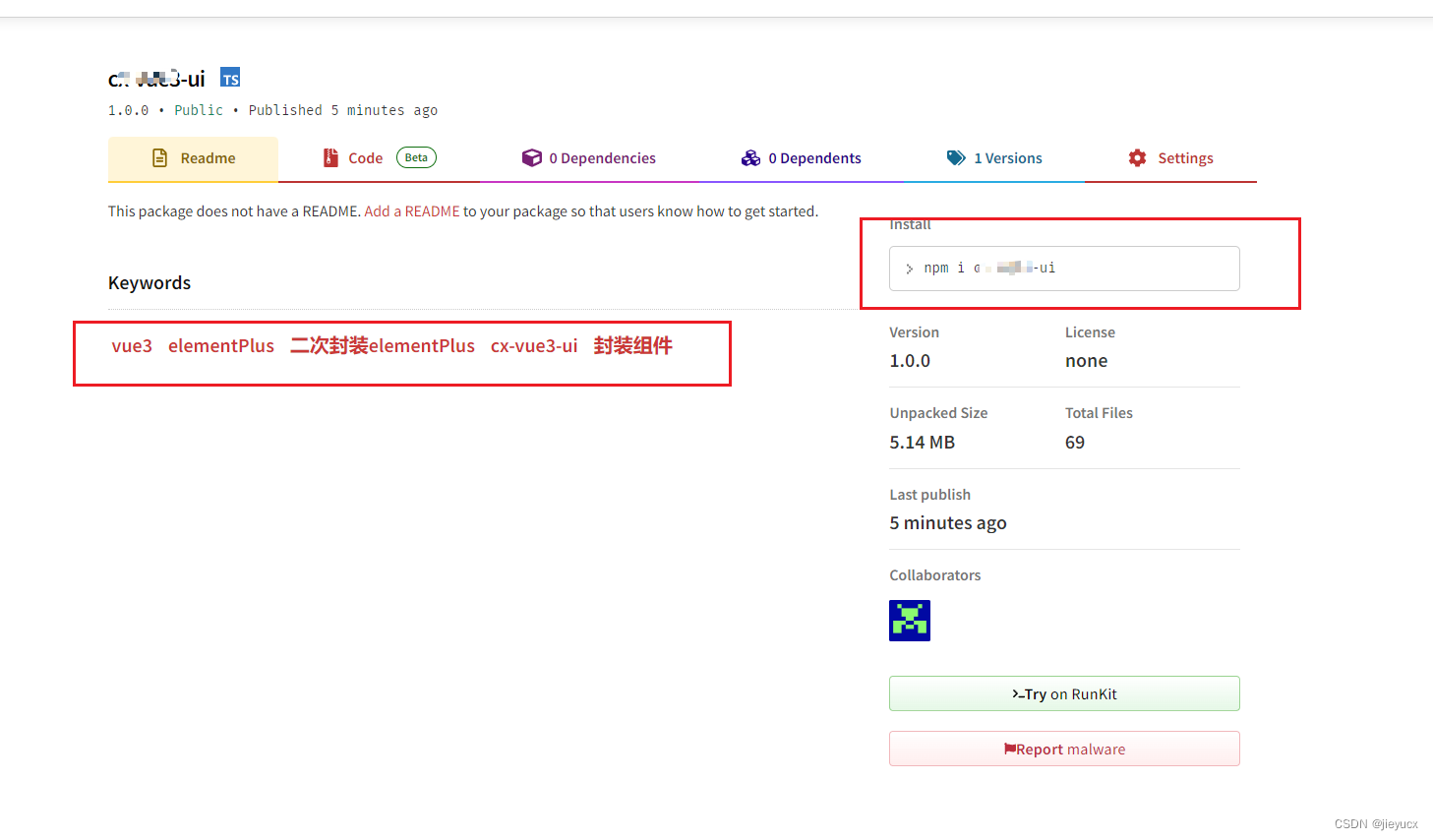
发布npm包流程
发布npm包的步骤如下: 在终端中通过 npm init 命令创建一个新的npm包,按照提示填写包的信息,如包名称、版本、描述、作者、许可证等。 在包的根目录下创建一个 index.js 文件,编写你的代码。 确认你已经注册了npm账号࿰…...
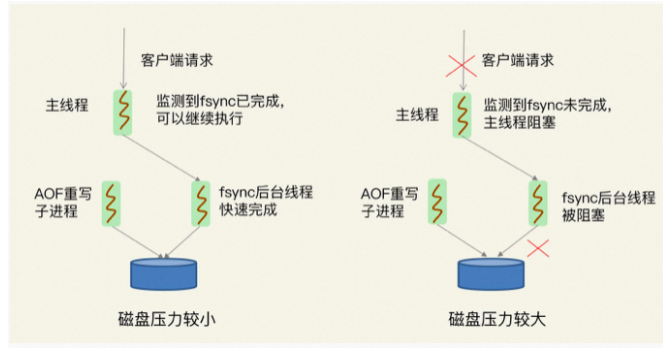
面试官:Redis 为什么变慢了?怎么解决?
一、Redis为什么变慢了 二、Redis如何优化 三、Redis变慢了排查步骤 一、Redis为什么变慢了 1.Redis真的变慢了吗? 对 Redis 进行基准性能测试 例如,我的机器配置比较低,当延迟为 2ms 时,我就认为 Redis 变慢了,…...

Docker:开启应用程序开发新篇章的利器
Docker:开启应用程序开发新篇章的利器 引言:1. Docker 的基本概念2. Docker 的优势3. Docker 在应用程序开发中的实际应用如何创建docker镜像如何部署docker镜像结论: 引言: 在现代软件开发领域中,容器化技术正在迅猛…...

Python面向对象(三)(继承、封装)
面向对象的三大特性 面向对象编程,是许多编程语言都支持的一种编程思想。 简单理解是:基于模板(类)去创建实体(对象),使用对象完成功能开发。 面向对象包含3大主要特性: 封装 封…...
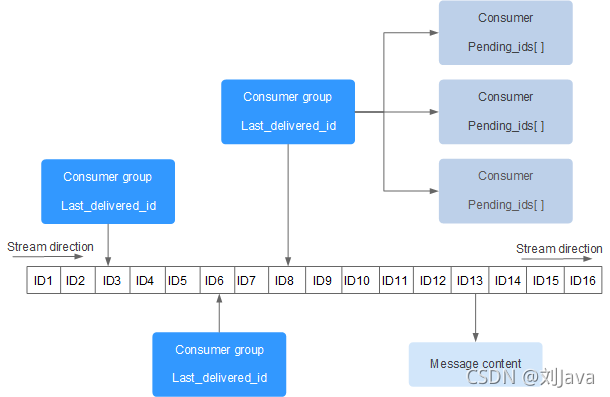
Redis Stream 流的深度解析与实现高级消息队列【一万字】
详细介绍了 Redis 5.0 版本新增加的数据结构Stream的使用方式以及原理,如何实现更加可靠的消息队列。 文章目录 Stream 概述2 Stream基本结构3 存储数据3.1 Entry ID3.2 数量限制 4 获取数据4.1 范围查询4.2 独立消费消息4.2.1 非阻塞使用4.2.2 阻塞的使用 4.3 消费…...

一个灵活、现代的Android应用架构
一个灵活、现代的Android应用架构 学习Android架构的原则:学习原则,不要盲目遵循规则。 本文旨在通过示例演示实际应用:通过示范Android架构来进行教学。最重要的是,这意味着展示出如何做出各种架构决策。在某些情况下࿰…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...
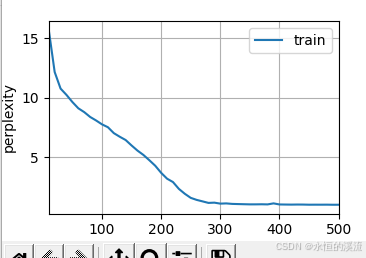
李沐--动手学深度学习--GRU
1.GRU从零开始实现 #9.1.2GRU从零开始实现 import torch from torch import nn from d2l import torch as d2l#首先读取 8.5节中使用的时间机器数据集 batch_size,num_steps 32,35 train_iter,vocab d2l.load_data_time_machine(batch_size,num_steps) #初始化模型参数 def …...

raid存储技术
1. 存储技术概念 数据存储架构是对数据存储方式、存储设备及相关组件的组织和规划,涵盖存储系统的布局、数据存储策略等,它明确数据如何存储、管理与访问,为数据的安全、高效使用提供支撑。 由计算机中一组存储设备、控制部件和管理信息调度的…...

【PX4飞控】mavros gps相关话题分析,经纬度海拔获取方法,卫星数锁定状态获取方法
使用 ROS1-Noetic 和 mavros v1.20.1, 携带经纬度海拔的话题主要有三个: /mavros/global_position/raw/fix/mavros/gpsstatus/gps1/raw/mavros/global_position/global 查看 mavros 源码,来分析他们的发布过程。发现前两个话题都对应了同一…...
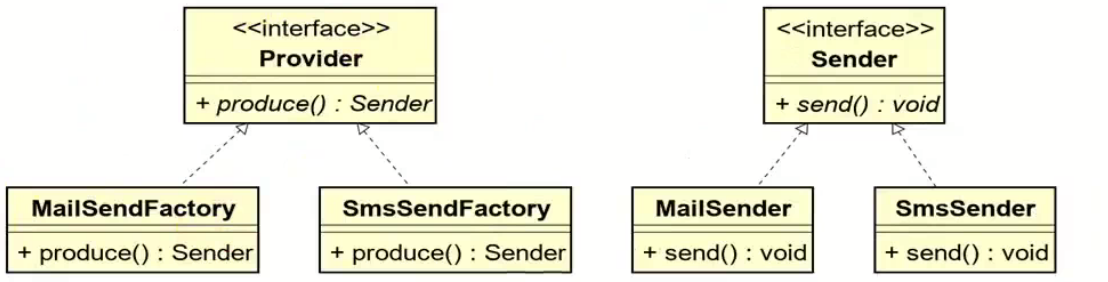
工厂方法模式和抽象工厂方法模式的battle
1.案例直接上手 在这个案例里面,我们会实现这个普通的工厂方法,并且对比这个普通工厂方法和我们直接创建对象的差别在哪里,为什么需要一个工厂: 下面的这个是我们的这个案例里面涉及到的接口和对应的实现类: 两个发…...
