【【51单片机LCD1602模块介绍】】
LCD1602的介绍
显示容量16x2 每个字符是5x7的点阵
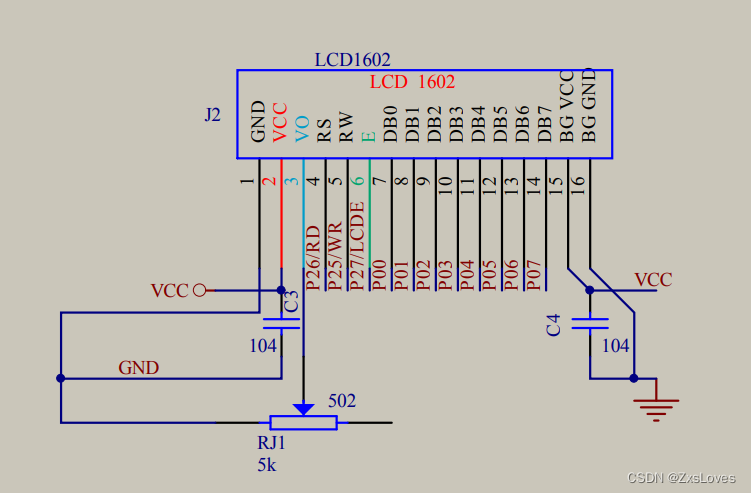
VDD 是电源正极 4.5-5.5v
VO 是对比度调节电压
RS 数据/指令 选择 1为数据0为指令
RW 读写选择1是读 0为写
E 使能 1为数据有效 下降沿执行命令
D0-D7 数据输入输出
A 背光电源正极 K 背光电源负极
LCD1602的操作流程
1.初始化:
发送0x38//八位数据接口,两行显示,5*7点阵
发送指令0x0C //显示开,光标关,闪烁关
发送指令0x06 //数据读写操作后,光标自动加1,画面不动
发送指令0x01 // 清屏
2.显示字符
发送指令0x80|AC //设置光标位置
发送数据 //发送想要显示的字符数据
发送数据 // 发送想要显示的字符数据
相关文章:

【【51单片机LCD1602模块介绍】】
LCD1602的介绍 显示容量16x2 每个字符是5x7的点阵 VDD 是电源正极 4.5-5.5v VO 是对比度调节电压 RS 数据/指令 选择 1为数据0为指令 RW 读写选择1是读 0为写 E 使能 1为数据有效 下降沿执行命令 D0-D7 数据输入输出 A 背光电源正极 K 背光电源负极 LCD1602的操作流程 1.初始…...
文件处理)
【Nginx11】Nginx学习:HTTP核心模块(八)文件处理
Nginx学习:HTTP核心模块(八)文件处理 继续我们的 HTTP 核心模块之旅。今天主要是文件相关的一些处理操作,包括 DirectIO、文件缓存以及 sendfile 相关的配置。这三个配置中,大家应该会见过 sendfile ,但是另…...
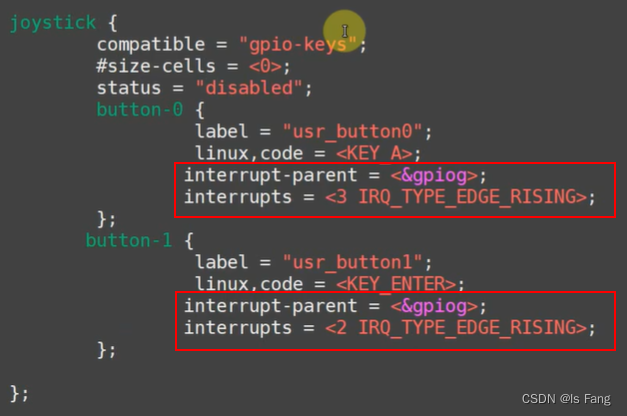
STM32MP157驱动开发——按键驱动(休眠与唤醒)
文章目录 “休眠-唤醒”机制:APP执行过程内核函数休眠函数唤醒函数 休眠与唤醒方式的按键驱动程序(stm32mp157)驱动程序框架button_test.cgpio_key_drv.cMakefile修改设备树文件编译测试 “休眠-唤醒”机制: 当应用程序必须等待某个事件发生,…...

全面解析 SOCKS5 代理与 HTTP 代理的对比与应用
一、 SOCKS5 代理与 HTTP 代理的基本原理 SOCKS5 代理:SOCKS5 是一种网络协议,它可以在传输层(Transport Layer)代理 TCP 和 UDP 请求。SOCKS5 代理不解析请求内容,而是直接将数据中转至目标服务器,支持更广…...

STM32 HEX文件和BIN文件格式区别keil中的配置与生成
一、区别 HEX 文件: 是包括地址信息的,在烧写或下载HEX文件的时候,一般都不需要用户指定地址,因为HEX文件内部的信息已经包括了地址。HEX文件是用ASCII来表示二进制的数值。例如一般8-BIT的二进制数值0x3F,用ASCII来表示就需要分别表示字符3和字符F,每个字符需要一个BYTE…...

RabbitMQ优先级队列的使用
RabbitMQ优先级队列的使用 生产者 public class PriorityQueue {public static void Send(){string path AppDomain.CurrentDomain.BaseDirectory;string tag path.Split(/, \\).Last(s > !string.IsNullOrEmpty(s));Console.WriteLine($"这里是 {tag} 启动了。。&…...

MAC 推送证书不受信任
配置推送证书的时候,一打开就变成不受信任,搜了很多解决版本。 由于苹果修改相关规定,推送证书 打开Apple PKI - Apple 下载AppleWWDRCA文件,选择G4,双击安装之后,证书已经变为受信任。 AppleWWDRCA(Apple Worldwid…...

Gitee创建分支
在使用Gitee进行代码托管时,分支是一个非常重要的概念。它可以让我们在不同的开发阶段、不同的团队成员之间协作开发,提高团队工作效率。因此,下面将介绍如何在Gitee仓库中建立分支。 一、在Gitee上创建新的分支 在讲解如何在Gitee上创建新…...

集群间ssh配置免密登录
ssh免密配置,可以将ssh生成的密钥分发给目标主机,之后再用ssh访问目标主机时就无需输入密码 下面我们来配置用centos71免密登录centos72主机 使用下面指令生成一个密钥 ssh-keygen其中会提示,是否输入密码短语,这里不输入&#…...

YOLOV8改进:CVPR 2023 | SCConv: 即插即用的空间和通道重建卷积
1.该文章属于YOLOV5/YOLOV7/YOLOV8改进专栏,包含大量的改进方式,主要以2023年的最新文章和2022年的文章提出改进方式。 2.提供更加详细的改进方法,如将注意力机制添加到网络的不同位置,便于做实验,也可以当做论文的创新点。 2.涨点效果:添加 SCConv,经过测试,有效涨点。…...
人员定位安全管控系统:提升安全管理水平的智能解决方案
在当今社会,人员安全管理成为各行各业关注的焦点。为了保障人员的安全和提高管理效率,人员定位安全管控系统应运而生。 人员定位安全管控系统采用多种定位技术来实现对人员位置的准确定位,如GPS(全球定位系统)、Wi-Fi…...
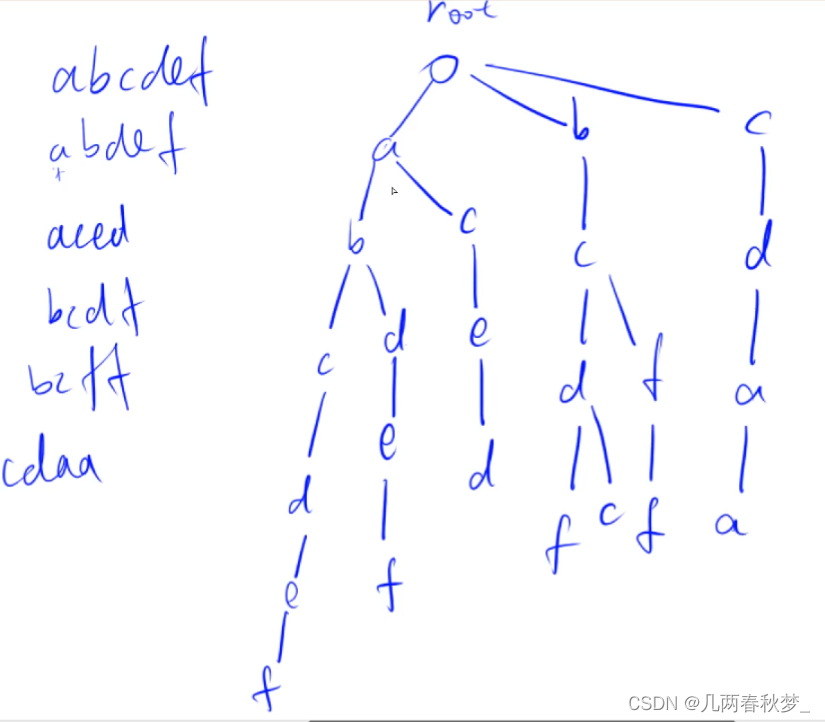
数据结构(二)
目录 Trie树 并查集 堆 Trie树 作用:用来高效地存储和查找字符串集合的数据结构 基本形式: 模板代码如下: #include<iostream> using namespace std;const int N 100010;//idx代表当前用到哪个下标 //既是根节点,又是空节点 //cnt存储的是以当前点结尾的…...
推送到logstash(spring boot + logback+ logstash))
logback 自定义log字段(MDC)推送到logstash(spring boot + logback+ logstash)
直接上代码: 1.创建FIlter,往 MDC 里面追加内容 WebFilter Component public class LogBackFilter implements Filter {Overridepublic void init(FilterConfig filterConfig) throws ServletException {}Overridepublic void doFilter(ServletRequest…...

1253. 重构 2 行二进制矩阵
1253. 重构 2 行二进制矩阵 给你一个 2 行 n 列的二进制数组: 矩阵是一个二进制矩阵,这意味着矩阵中的每个元素不是 0 就是 1。第 0 行的元素之和为 upper。第 1 行的元素之和为 lower。第 i 列(从 0 开始编号)的元素之和为 cols…...
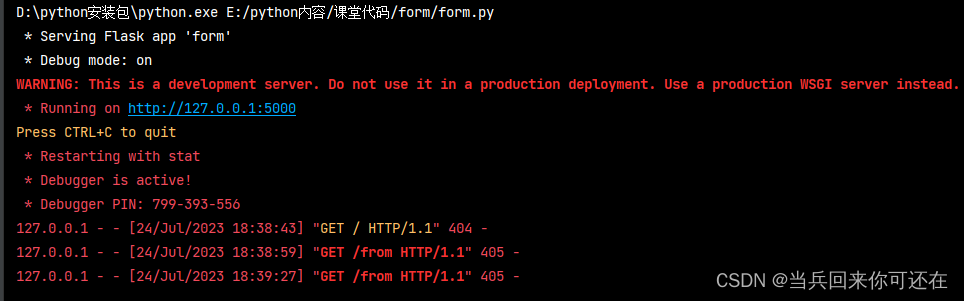
安全—01day
文章目录 1. 编码1.1 ASCLL编码1.2 URL编码1.3 Unicode编码1.4 HTML编码1.5 Base64编码 2. form表单2.1 php接收form表单2.2 python接收form表单 1. 编码 1.1 ASCLL编码 ASCII 是基于拉丁字母的一套电脑编码系统,主要用于显示现代英语和其他西欧语言。它是最通用的…...

【Git】Please commit your changes or stash them before you merge的解决方法
背景 我从远程库中clone了一个项目进行开发,修改了一部分代码后,远程库有更新,我想将远程更新拉取下来,并且保留自己的更改,使用git pull origin master命令,有报错: error: Your local chang…...
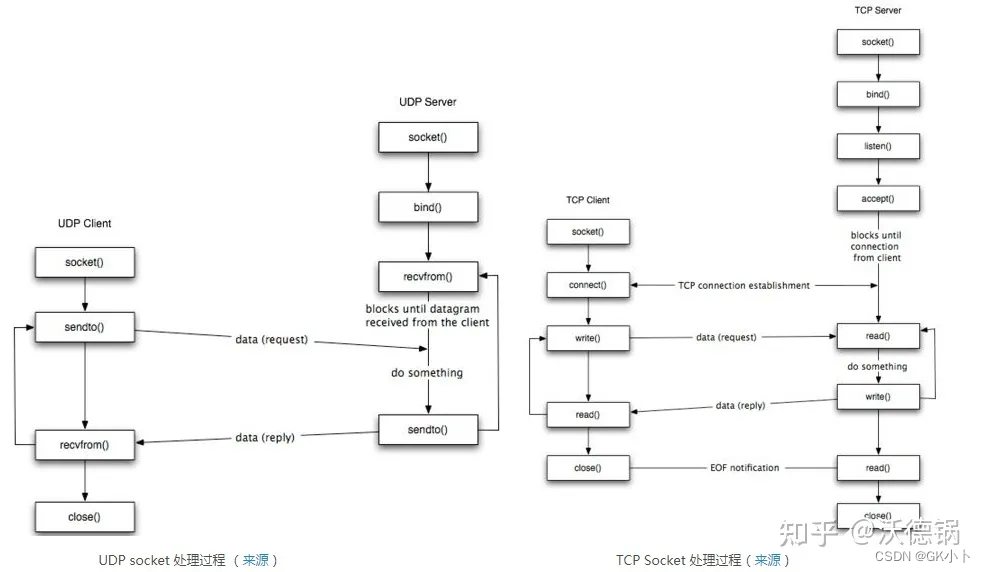
网卡收发包系统结构收发包流程,tcp/ip协议,socket套接字缓冲区,滑动窗口,mtu/mss
MTU和MSS的区别 MTU和MSS的区别 TCP 的 MTU & MSS MTU是在那一层?MSS在那一层? MTU是在数据链路层的载荷大小也就是传给网络层的大小,mss是在传输层的载荷大小也就是传给应用层的大小 mss是根据mtu得到的 1、MTU: Maximu…...

VUE之axios使用,跨域问题,拦截器添加Token
参考资料: 参考视频 视频资料及个人demo Axios中文文档 VUE之基本部署及VScode常用插件 VUE之基本组成和使用 VUE之Bootstrap和Element-UI的使用 准备工作: 关于SpringBoot和SpringCloud的搭建,以及mybatis-plus的整合见本人之前的CSDN博客,下面编写get请求和post请求…...
)
阿里云函数计算签名认证(iOS实现细节备注)
1、使用第三方库 AFNetworking进行网络请求。 2、阿里云函数计算签名认证文档 3、文档中添加 CanonicalizedFCHeaders 可以不用添加,CanonicalizedResource如何没有设置Path,在末尾加入“/”就可以了。 4、主要还是 hmac-sha256 签名认证,在实…...

成都爱尔蔡裕:泡在“糖”里的脆弱血管,暴露在眼睛深处
糖尿病是一组由多病因引起的以慢性高血糖为特征的终身性代谢性疾病。长期血糖增高,大血管、微血管受损并危及心、脑、肾、周围神经、眼睛、足等。医生临床数据显示,糖尿病发病后10年左右,将有30%~40%的患者至少会发生一种并发症&a…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

GeoServer发布PostgreSQL图层后WFS查询无主键字段
在使用 GeoServer(版本 2.22.2) 发布 PostgreSQL(PostGIS)中的表为地图服务时,常常会遇到一个小问题: WFS 查询中,主键字段(如 id)莫名其妙地消失了! 即使你在…...
