E. Nastya and Potions(DFS+记忆化搜索)
炼金术士纳斯蒂亚喜欢混合药剂。一共有n种药剂,ci硬币可以买到一种 i 型药剂。 任何一种药剂都只能通过一种方式获得,即混合其他几种药剂。混合过程中使用的药剂将被消耗掉。此外,任何药剂都不能通过一个或多个混合过程从自身获得。
作为一名经验丰富的炼金术士,Nastya拥有无限量的k种药剂p1、p2、…、pk,但她不知道下一步要获得哪一种。为了做出决定,她要求你为每1≤i≤n找到她下一次获得 i 型药剂所需的最低硬币数量。
输入:
每个测试的第一行包含一个整数t(1≤t≤10^4)——测试用例的数量。每个测试用例描述如下:
第一行包含两个整数n和k(1≤k<n≤2‧10^5)——药剂类型的总数和Nastya已经拥有的药剂类型的数量。
第二行包含n个整数c1、c2、…、cn(1≤ci≤10^9)——购买药剂的成本。
第三行包含k个不同的整数p1,p2,…,pk(1≤pi≤n)——药剂的指数Nastya已经有了无限的供应。
接下来是描述通过混合获得药剂的方法的n行。每行以整数mi(0≤mi<n)开始——混合类型 i(1≤i≤n)的药剂所需的药剂数量。然后这行包含mi不同的整数e1、e2、…、emi(1≤ej≤n ,ej≠i)——混合Ⅱ型药剂所需的药剂指数。如果此列表为空,则只能购买类型为 i 的药剂。保证不会通过一个或多个混合过程从自身获得任何药剂。保证所有测试用例的所有nn值之和不超过2∙10^5。同样,保证所有测试用例中所有mi值的总和不超过2∙10^5。
输出:
对于每个测试用例,输出n个整数——Nastya获得每种类型的药剂所需花费的最小硬币数。
输入样例:
4
5 1
30 8 3 5 10
3
3 2 4 5
0
0
2 3 5
0
3 2
5 143 3
1 3
1 2
0
2 1 2
5 1
5 4 1 3 4
2
2 4 5
3 3 5 4
2 1 4
1 5
0
4 2
1 1 5 4
2 4
3 2 4 3
0
2 2 4
1 2
输出样例
23 8 0 5 10 0 143 0 5 0 1 3 4 0 0 0 0
输入样例:
3
6 3
5 5 4 5 2 2
3 4 5
2 2 5
1 5
3 4 1 6
4 2 6 1 5
0
0
6 2
1 4 4 1 5 2
3 6
4 6 3 4 5
4 6 5 3 4
0
1 5
1 6
0
2 1
4 3
1
0
1 1
输出样例:
0 0 0 0 0 2 0 0 0 0 0 0 0 0
#include<iostream>
#include<algorithm>
#include<vector>
#include<cstring>
using namespace std;
const int N=2e5+10;
long long dp[N];
long long c[N];
vector<int>v[N];
int dfs(int x)
{if(dp[x]!=-1) return dp[x];if(v[x].size()==0){dp[x]=c[x];return dp[x];}long long sum=0;for(int i=0;i<v[x].size();i++){sum+=dfs(v[x][i]);}dp[x]=min(sum,c[x]);return dp[x];
}
int main()
{int t;cin>>t;while(t--){int n,k;cin>>n>>k;memset(dp,-1,sizeof dp);for(int i=1;i<=n;i++){cin>>c[i];v[i].clear();}for(int i=1;i<=k;i++){int x;cin>>x;c[x]=0;}for(int i=1;i<=n;i++){int num;cin>>num;for(int j=1;j<=num;j++){int x;cin>>x;v[i].push_back(x);}}for(int i=1;i<=n;i++) cout<<dfs(i)<<" ";cout<<endl;}return 0;
}
相关文章:
)
E. Nastya and Potions(DFS+记忆化搜索)
炼金术士纳斯蒂亚喜欢混合药剂。一共有n种药剂,ci硬币可以买到一种 i 型药剂。 任何一种药剂都只能通过一种方式获得,即混合其他几种药剂。混合过程中使用的药剂将被消耗掉。此外,任何药剂都不能通过一个或多个混合过程从自身获得。 作为一名…...

什么是tcp rst以及什么时候产生?
rst包是仅在header control bits设置rst的空payload包,用于强制关闭tcp连接。常在以下场景发送 远程主机没有监听该端口 远程主机强迫关闭了一个现有连接。比如服务端进程崩溃后重启会向之前连接发送rst 相比于四次挥手的fin,rst是在异常情况下的无条…...
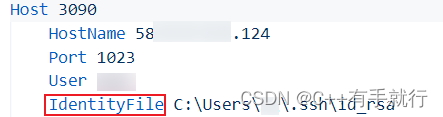
Visual Studio Code配置免密远程开发环境
VSCode安装插件 要是想连接远程服务器,先在本地安装下面的插件(红色圈起来的需要装) 连接远程服务器 配置服务器信息 保存然后再连接,输入密码,如果能连接上说明是没问题的,下面开始免密登录 免密配置 客…...
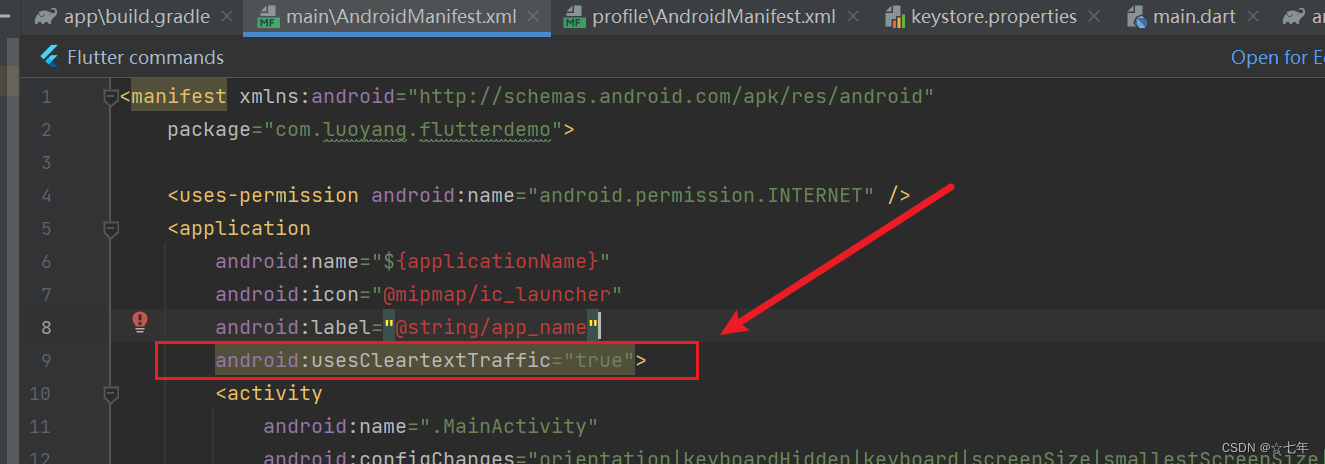
flutter android Webview 打开网页错误ERR_CLEARTEXT_NOT_PERMITTED 、 net:ERR_CACHE_MISS
当你在Flutter应用中尝试打开一个非安全连接的网页(例如HTTP连接而不是HTTPS连接)时,可能会遇到"ERR_CLEARTEXT_NOT_PERMITTED"错误。这是因为默认情况下,Android 9及更高版本禁止应用程序通过非安全的明文HTTP连接进行…...

ARP协议(地址解析协议)
文章目录 ARP协议(地址解析协议)MAC地址ARP协议ARP具体实现同一链路不同链路 ARP 缓存缓存查询 APR请求/响应报文 ARP协议(地址解析协议) MAC地址 MAC 地址的全称是 Media Access Control Address,即媒体访问控制地址…...

【贪心算法】334. 递增的三元子序列
334. 递增的三元子序列 解题思路 找到的递增序列 不一定是连续的固定第一个数first 然后开始向后找第二个数second要求second 大于 first 找到之后 向后找第三个数third 找到 返回true如果third < first 那么更新first third 重新找如果只是third > first 更新second …...

react实现路由跳转动画
下载插件 npm i react-transition-group 配置路由 import { createBrowserRouter as ReactRouter,Navigate } from "react-router-dom";import App from ../App.js import Login from "../view/login.js"; import Home from "../home.js"; co…...
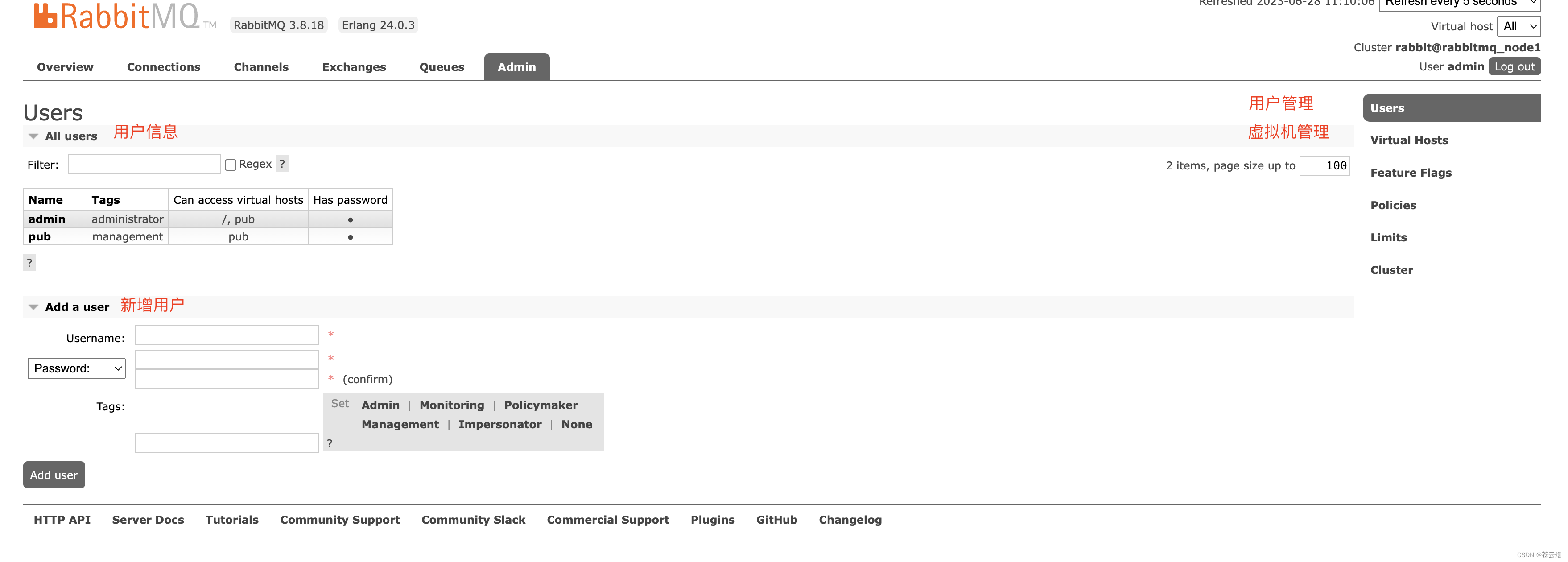
(二)RabbitMQ【安装Erlang、安装RabbitMQ 、账户管理、管控台、Docker安装 】
Lison <dreamlison163.com>, v1.0.0, 2023.06.22 RabbitMQ【安装Erlang、安装RabbitMQ 、账户管理、管控台、Docker安装 】 文章目录 RabbitMQ【安装Erlang、安装RabbitMQ 、账户管理、管控台、Docker安装 】**安装Erlang**安装RabbitMQ账户管理管控台Docker安装RabbitM…...
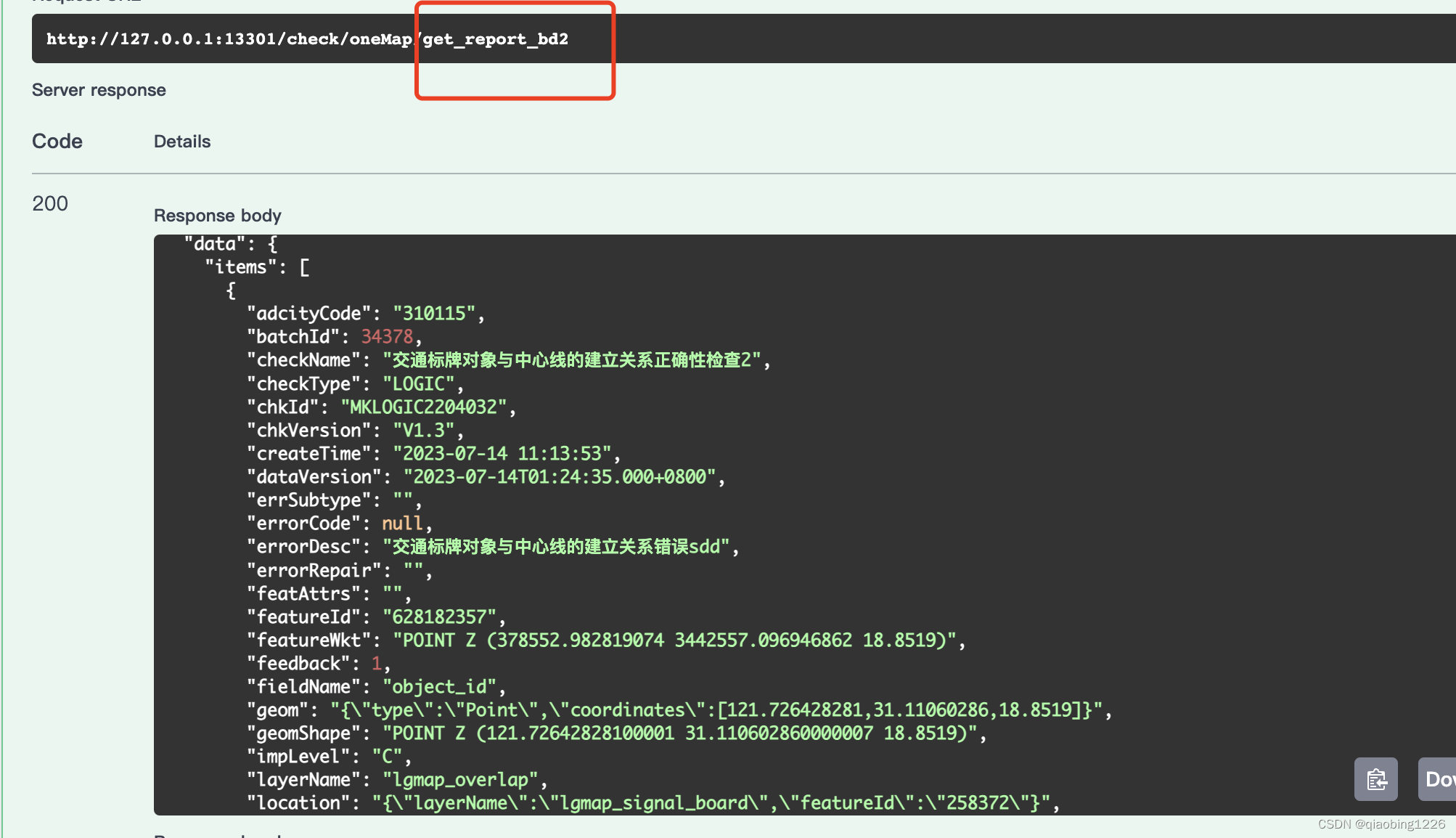
springboot mybatis-plus 多数据源配置(HikariCP)
1.导入依赖jar <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-jdbc</artifactId></dependency><dependency><groupId>org.postgresql</groupId><artifactId>postgres…...
跃焱邵隼网站demo
xdm 网站的代码开源了。 今年迷上摄影和剪辑了,所以很少投入到网站的维护。 然后经过群友的一些反馈,所以决定 将网站上demo开源放出来了。 后面有机会再出一些好玩的东西。 哦 对了 3d 编辑器我已经融入地图了 年底搞一些好玩的东西出来。 可以关注…...
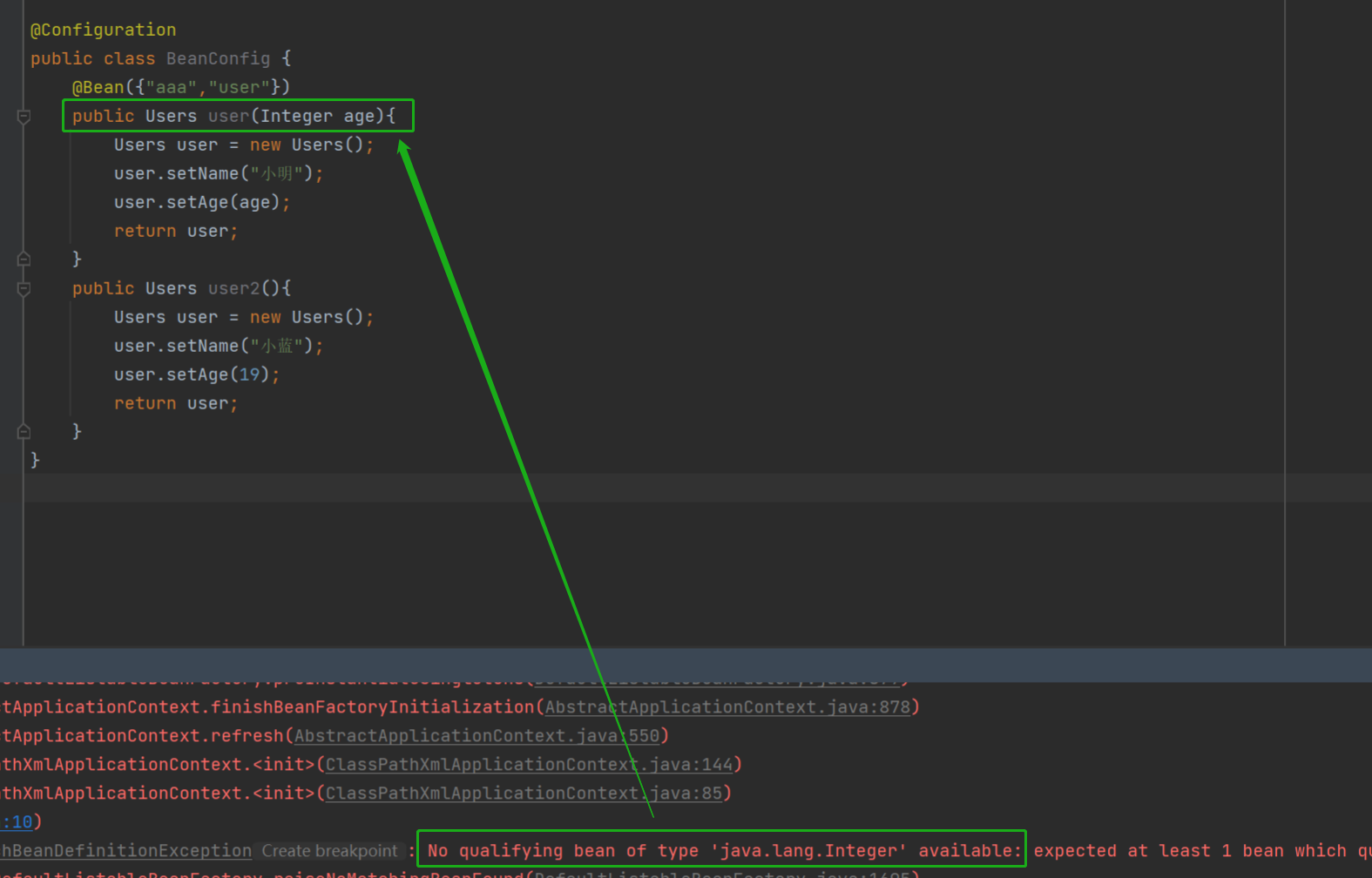
3. Spring 更简单的读取和存储对象(五大类注解 方法注解)
目录 1. 存储 Bean 对象 1.1 配置扫描路径 1.2 添加注解存储 Bean 对象 1.2.1 Controller(控制器存储) 1.2.2 Service(服务存储) 1.2.3 Repository(仓库存储) 1.2.4 Component(组件存储&…...

TypeScript基础篇 - 泛型
目录 泛型的概念 接口是对方面的描述(Aspect),继承其中几个方法。重定义方法 泛型是对共性的提取 泛型(Generics) 泛型的例子 泛型类 推荐写法 泛型约束 keyof操作符 泛型的特化(实例化ÿ…...

C++ 常量
常量是固定值,在程序执行期间不会改变。这些固定的值,又叫做字面量。 常量可以是任何的基本数据类型,可分为整型数字、浮点数字、字符、字符串和布尔值。 常量就像是常规的变量,只不过常量的值在定义后不能进行修改。 整数常量…...

智安网络|实现数据安全:探索数据动态脱敏的落地策略
在当今数字化时代,数据安全成为企业和组织管理中的头等大事。然而,数据共享和数据大规模处理的需求也日益增长,这就需要在数据传输和存储过程中采取措施来保护用户的隐私。数据动态脱敏技术应运而生,为解决数据隐私和保护的问题提…...
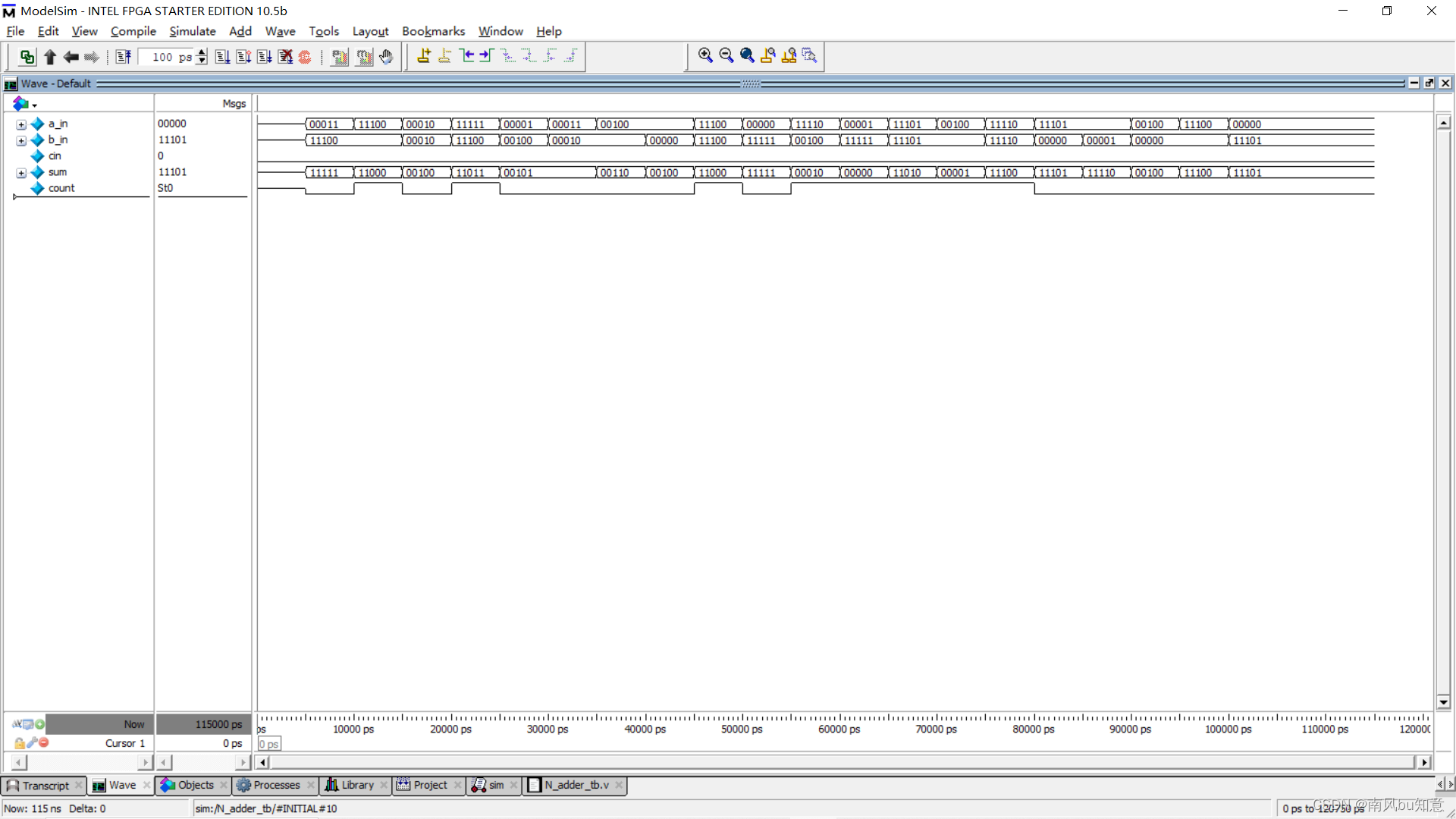
全加器(多位)的实现
一,半加器 定义 半加器(Half Adder)是一种用于执行二进制数相加的简单逻辑电路。它可以将两个输入位的和(Sum)和进位(Carry)计算出来。 半加器有两个输入:A 和 B,分别代表…...

Clion开发stm32之微妙延迟(采用nop指令实现)
前言 需要借助逻辑分析仪动态调整参数此次测试的开发芯片为stm32f103vet6 延迟函数 声明 #define NOP_US_DELAY_MUL_CNT 5 /*nop 微妙延迟需要扩大的倍数(根据实际动态修改)*/ void bsp_us_delay_nop(uint32_t us);void bsp_ms_delay_nop(uint32_t ms);定义 void bsp_us_dela…...
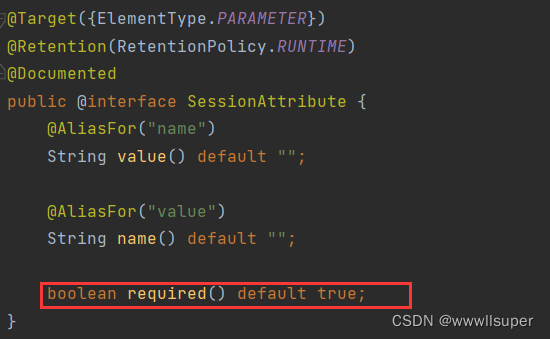
Spring MVC -- 获取参数(普通对象+JSON对象+URL地址参数+文件+Cookie/Session/Header)
目录 1.获取参数 1.1获取单个参数 1.2获取多个参数 传参注意事项: 2.获取对象 3.后端参数重命名RequestParam 4.获取JSON对象RequestBody 5.从 URL 地址中获取参数 PathVariable 6.上传文件 RequestPart 7.获取Cookie/Session/Header 7.1 获取 Request 和…...

Langchain 的 Conversation summary memory
Langchain 的 Conversation summary memory 现在让我们看一下使用稍微复杂的内存类型 - ConversationSummaryMemory 。这种类型的记忆会随着时间的推移创建对话的摘要。这对于随着时间的推移压缩对话中的信息非常有用。对话摘要内存对发生的对话进行总结,并将当前摘…...

Safari 查看 http 请求
文章目录 1、开启 Safari 开发菜单2、显示 JavaScript 控制台 1、开启 Safari 开发菜单 Safari 设置中,打开开发菜单选项 *** 选择完成后,Safari 的目录栏就会出现一个 开发 功能。 2、显示 JavaScript 控制台 开启页面后,在开发中选中 显…...

kafka权限控制功能
参考链接: https://www.clougence.com/cc-doc/dataMigrationAndSync/database/privs_for_kafka Kafka需要的权限 | CloudCanal of ClouGence Kafka Topic 权限控制可以通过使用 Apache Kafka 的内置安全特性来实现。这主要涉及到两个方面:认证&#…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...
