【LeetCode热题100】打卡第44天:倒数第30~25题
文章目录
- 【LeetCode热题100】打卡第44天:倒数第30~25题
- ⛅前言
- 移动零
- 🔒题目
- 🔑题解
- 寻找重复数
- 🔒题目
- 🔑题解
- 二叉树的序列化与反序列化
- 🔒题目
- 🔑题解
- 最长递增子序列
- 🔒题目
- 🔑题解
- 删除无效括号
- 🔒题目
- 🔑题解
【LeetCode热题100】打卡第44天:倒数第30~25题
⛅前言
大家好,我是知识汲取者,欢迎来到我的LeetCode热题100刷题专栏!
精选 100 道力扣(LeetCode)上最热门的题目,适合初识算法与数据结构的新手和想要在短时间内高效提升的人,熟练掌握这 100 道题,你就已经具备了在代码世界通行的基本能力。在此专栏中,我们将会涵盖各种类型的算法题目,包括但不限于数组、链表、树、字典树、图、排序、搜索、动态规划等等,并会提供详细的解题思路以及Java代码实现。如果你也想刷题,不断提升自己,就请加入我们吧!QQ群号:827302436。我们共同监督打卡,一起学习,一起进步。
博客主页💖:知识汲取者的博客
LeetCode热题100专栏🚀:LeetCode热题100
Gitee地址📁:知识汲取者 (aghp) - Gitee.com
题目来源📢:LeetCode 热题 100 - 学习计划 - 力扣(LeetCode)全球极客挚爱的技术成长平台
PS:作者水平有限,如有错误或描述不当的地方,恳请及时告诉作者,作者将不胜感激
移动零
🔒题目
原题链接:283.移动零
🔑题解
-
解法一:暴力枚举即可
但是我们使用
copyOfRange方法存在一个弊端,它会重现创建一个数组,然后将值赋值给新的数组引用,给不是在原有的数组引用上进行赋值,所以这里就导致最终无法修改到我们要实现效果的数组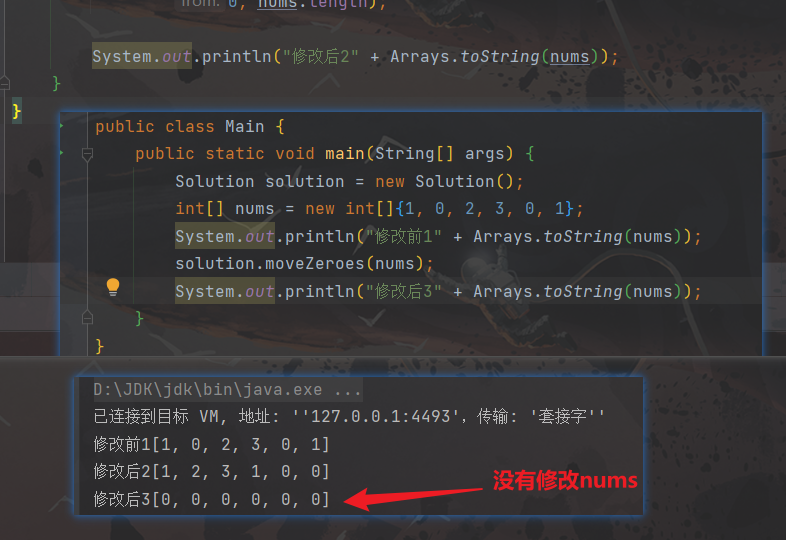
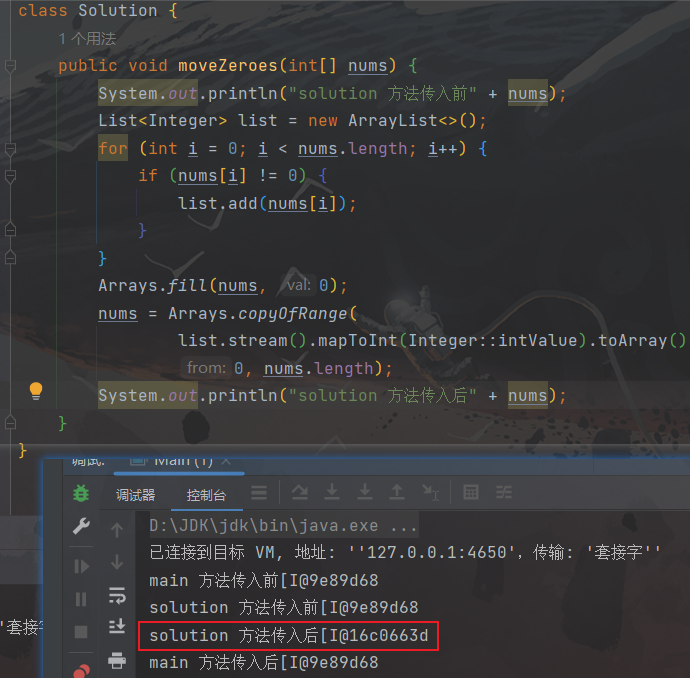
下方代码,最终输出的nums全部是 0
/*** @author ghp* @title* @description*/ class Solution {public void moveZeroes(int[] nums) {List<Integer> list = new ArrayList<>();for (int i = 0; i < nums.length; i++) {if (nums[i] != 0){list.add(nums[i]);}}Arrays.fill(nums, 0);nums = Arrays.copyOfRange(list.stream().mapToInt(Integer::intValue).toArray(),0, nums.length);} }复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( n ) O(n) O(n)
其中 n n n 为数组中元素的个数
解决方法:使用for循环,逐个赋值(这里我就是使用lambda表达式实现,效果都是一样的,但是这种更加优雅)
/*** @author ghp* @title* @description*/ class Solution {public void moveZeroes(int[] nums) {List<Integer> list = new ArrayList<>();for (int i = 0; i < nums.length; i++) {if (nums[i] != 0) {list.add(nums[i]);}}Arrays.fill(nums, 0);IntStream.range(0, list.size()).forEach(i -> nums[i] = list.get(i));} } -
解法二:双指针
这个思路是非类似于快排的那个划分左右区间,设置两个指针,使得左区间都比主元小,右区间都比主元大或等。
这里我们相当于是把0当作主元,左区间都是不等于0的,右区间都是等于0的
class Solution {public void moveZeroes(int[] nums) {int i = 0;// 遍历数组,将非0元素放到i的左侧for (int j = 0; j < nums.length; j++) {if (nums[j] != 0){// 当前元素不等于0,将非0元素放到i的左侧int t = nums[j];nums[j] = nums[i];nums[i] = t;i++;}}} }复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( 1 ) O(1) O(1)
其中 n n n 为数组中元素的个数
寻找重复数
🔒题目
原题链接:287.寻找重复数
🔑题解
本题总共有以下解法:
-
需要额外空间,需要修改原始数组:排序
-
需要额外空间,不需要修改原始数组:计数法、哈希表
-
不需要额外空间,需要修改原始数组:标记法、索引排序
-
不需要额外空间,不需要修改原始数组:暴力枚举、二分查找、位运算、快慢指针
PS:本文只讲解了二分查找、快慢指针、位运算三种能过且比较牛的方法,关于其它方法感兴趣都可以参考这篇文章:9种方法(可能是目前最全的),拓展大家思路 - 寻找重复数 - 力扣(LeetCode)
-
解法一:快慢指针(Floyd 判圈算法)
这个算法在前面已经多次遇到了,比如:第33天的环形链表、第34天的排序链表、第35天的相交链表、第40天的回文链表等都能看到快慢指针算法的身影。可能我们一下子无法直接联想到环形链表,这里我们画一个草图,将数组转换成一个环形链表(这是一种数学抽象,类似于七桥问题,把一个问题抽象成另一个与之等价的问题)
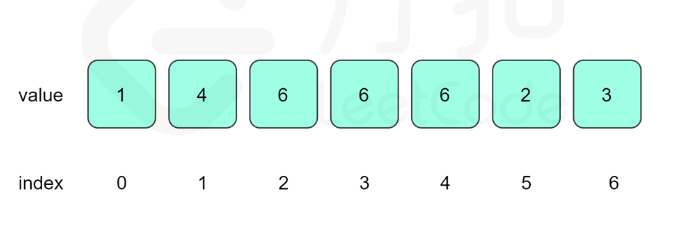
我们把数值的值当成链表的下一个节点,这个值与索引进行一个映射,从而可以通过上面的链表得到下面这个链表,此时我们把”要数组中的找重复元素“这个问题转换成"要找链表中环的入口节点",说到这里,如果你对环形链表这一题有经验的话,很快就能够解决了。如果你对环形链表不是很懂的话,可以参考这篇文章【LeetCode热题100】打卡第33天:环形链表
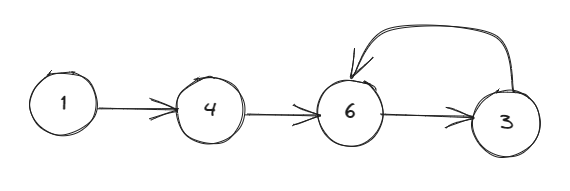
注意:本题能够使用快慢指针的前提是 1 < = n u m s [ i ] < = n 1<=nums[i]<=n 1<=nums[i]<=n,这样能够保障指针无论如何移动都不会出现索引越界
这里初略讲解以下如何定位环形链表的入环节点:
- 第一次遍历,fast比slow多走一步,寻找到fast和slow相等的节点,然后将fast重置到起始节点
- 第二次遍历,fast和slow走相同的步数,寻找到fast和slow相等的节点,此时fast和slow相遇的节点就是入环节点
至于详细证明思路,可以参考我上面给出的那个链接,链接的那篇文章中已给出比较详细的解答了
/*** @author ghp* @title* @description*/ class Solution {public int findDuplicate(int[] nums) {int fast = 0, slow = 0;do {fast = nums[nums[fast]];slow = nums[slow];} while (fast != slow);fast = 0;while (fast != slow) {fast = nums[fast];slow = nums[slow];}return fast;} }复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( 1 ) O(1) O(1)
其中n为数组中元素的个数
-
解法二:二分查找
本题主要用到了抽屉原理,简单来说就是把
10个苹果放进9个抽屉,至少有一个抽屉里至少放2个苹果。其此我们还需要寻找出有序的地方,本题有序的地方是隐式的,即比当前元素小的元素是有序的,只要发现这一点,其实就会变得很简单,但往往这一点一般很慢发现,这也是本题相较于其他显示有序的一个难点
我们新增一个变量
cnt[i]来记录当前数组中小于等于i的数有多少个,然后可以的发现cnt数组是有序的,对于有序数组我们①如果我们将
n个数放到n个位置上(数的范围是1~n),这些数不重复,则此时cnt==mid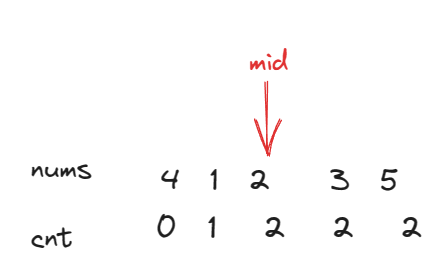
②如果我们将
n个数放到n+1个位置上(数的范围是1~n),这些数不重复,如果此时cnt<=mid,则说明重复的数一定在左侧区间,因为数是在1~n这个区间选的,cnt[n]<=mid说明比n小的数不到一半(正常情况是刚好一半的),根据抽屉原理,一定是有一个比mid小的数重复了,这样才会出现cnt[n]<=mid,所以重复的数在mid的左侧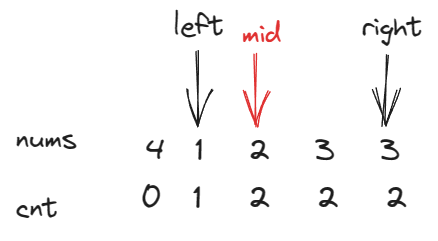
③如果我们将
n个数放到n+1个位置上,如果是左侧的数多了,则会导致cnt[n]>mid,此时我们可以在左侧区间寻找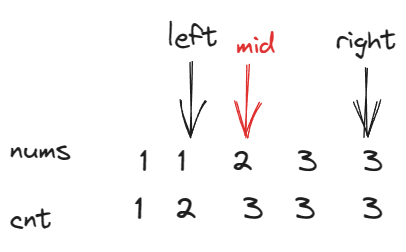
温馨提示:对于所有的二分查找,边界值都是需要十分注意的,这个我在以前总结的二分查找中就已经进行了详细讲解,这里我也不在赘述了,直接给出结论,如果想要了解的,可以参考我以前写的一篇关于二分查找边界值问题的总结
-
对于向下取整
mid = (right-left)/2 + left,如果取等while(left<=right),那么目标值在右right=mid-1,目标值在左left=mid+1 -
对于向下取整
mid=(right-left)/2 + left,如果不取等while(left<right),那么目标值在右right=mid,目标值在左left=mid+1如果取等匹配right=mid会导致死循环,如果不取等匹配right=mid-1会出现遗漏导致结果错误
/*** @author ghp* @title* @description*/ class Solution {public int findDuplicate(int[] nums) {int left = 1, right = nums.length - 1;while (left < right) {int mid = (right - left) / 2 + left;// 计算当前小于等于mid的元素有多少个int count = 0;for (int i = 0; i < nums.length; i++) {if (nums[i] <= mid){count++;}}if (count > mid){// 比mid小的元素超过了mid个,根据抽屉原理可以知道mid左侧出现了重复元素right = mid;}else{// 比mid小的元素超过了mid个,根据抽屉原理可以知道mid右侧出现了重复元素left = mid + 1;}}return left;} }复杂度分析:
- 时间复杂度: O ( n l o g n ) O(nlogn) O(nlogn)
- 空间复杂度: O ( 1 ) O(1) O(1)
其中n为数组中元素的个数
-
-
解法三:位运算
太强了,感兴趣的可以去看LeetCode官网,我先把前面两种解法消化吸收了
class Solution {public int findDuplicate(int[] nums) {int n = nums.length, ans = 0;int bit_max = 31;while (((n - 1) >> bit_max) == 0) {bit_max -= 1;}for (int bit = 0; bit <= bit_max; ++bit) {int x = 0, y = 0;for (int i = 0; i < n; ++i) {if ((nums[i] & (1 << bit)) != 0) {x += 1;}if (i >= 1 && ((i & (1 << bit)) != 0)) {y += 1;}}if (x > y) {ans |= 1 << bit;}}return ans;} }作者:LeetCode-Solution 链接:https://leetcode.cn/problems/find-the-duplicate-number/solution/xun-zhao-zhong-fu-shu-by-leetcode-solution/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。复杂度分析:
- 时间复杂度: O ( n l o g n ) O(nlogn) O(nlogn)
- 空间复杂度: O ( 1 ) O(1) O(1)
其中n为数组中元素的个数
二叉树的序列化与反序列化
🔒题目
原题链接:297.二叉树的序列化与反序列化
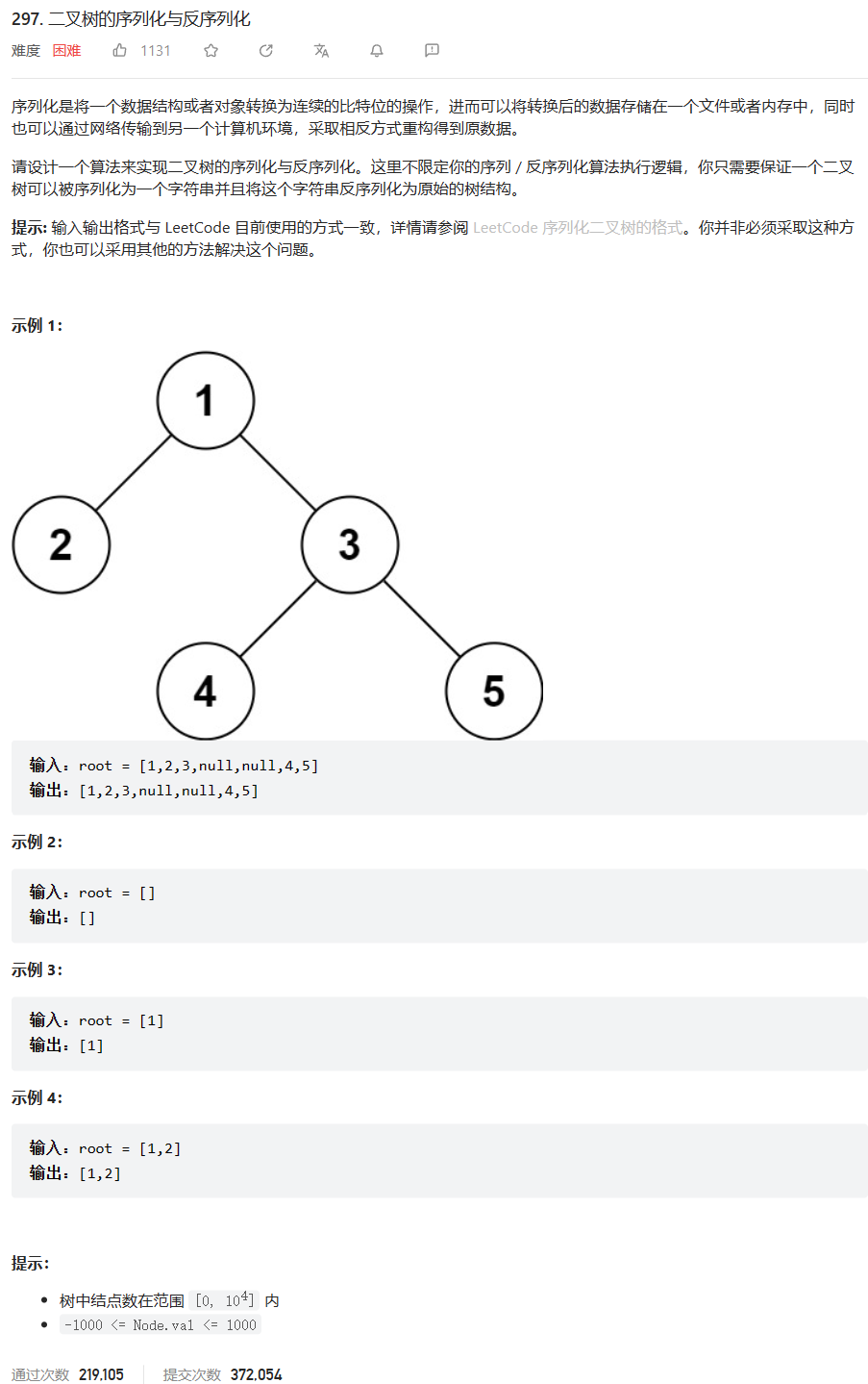
🔑题解
-
解法一:BFS(层序遍历)
不知道为什么我第一眼看着提感觉挺简单的,直接BFS不就好了吗,结果bug频出,一眨眼一小时就过去了,经过不断的debug最终成功完成了初步代码,并最终过了😄写这题的思路也比较简答, 直接使用BFS实现层序遍历即可
如果不会层序遍历的话,可以参考这篇文章:【LeetCode热题100】打卡第29天:二叉树的层序遍历
class Codec {public String serialize(TreeNode root) {if (root == null) {// 防止NPEreturn null;}// 存储每一层的节点的值StringBuilder ans = new StringBuilder(root.val + ",");// BFS层序遍历所有节点,将二叉树所有节点的值转存到ans中Deque<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode pre = queue.poll();TreeNode left = pre.left;if (left != null) {queue.offer(left);}ans.append(left == null ? "null" : left.val).append(",");TreeNode right = pre.right;if (right != null) {queue.offer(right);}ans.append(right == null ? "null" : right.val).append(",");}// 删除最后一个多余的逗号ans.deleteCharAt(ans.length() - 1);return ans.toString();}public TreeNode deserialize(String data) {if (data == null) {// 防止NPEreturn null;}// 将String转成List方便后续逻辑处理String[] dataStr = data.split(",");List<Integer> dataList = Arrays.stream(dataStr).map(str -> str.equals("null") ? null : Integer.valueOf(str)).collect(Collectors.toList());// BFS层序遍历所有节点,将层序遍历的字符串重新构建成一棵二叉树Deque<TreeNode> queue = new LinkedList<>();// 将根节点加入队列中TreeNode root = new TreeNode(dataList.get(0));queue.offer(root);dataList.remove(0);while (!dataList.isEmpty()) {TreeNode node = queue.poll();if (dataList.get(0) != null) {// 这里一定要判空,否则自动拆箱时会报NPE,下面那个判空也是一样的node.left = new TreeNode(dataList.get(0));queue.offer(node.left);}dataList.remove(0);if (dataList.isEmpty()) {// 防止NPEbreak;}if (dataList.get(0) != null) {node.right = new TreeNode(dataList.get(0));queue.offer(node.right);}dataList.remove(0);}return root;} }复杂度分析:
序列化
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( n ) O(n) O(n)
反序列化
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( n ) O(n) O(n)
其中 n n n 为二叉树节点的个数
代码优化:
对于serialize方法:
- 每个循环只需要处理一个节点,不需要额外的变量来保存父节点
对于deserialize方法:
- 使用整型数组代替列表,因为在循环中频繁进行插入和删除操作会导致列表的性能下降
- 使用索引标记当前节点的位置,避免频繁调用 dataList.get() 方法
/*** @author ghp* @title* @description*/ class Codec {public String serialize(TreeNode root) {if (root == null) {return null;}StringBuilder ans = new StringBuilder();Deque<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode node = queue.poll();if (node != null) {ans.append(node.val).append(",");queue.offer(node.left);queue.offer(node.right);} else {ans.append("null,");}}ans.deleteCharAt(ans.length() - 1);return ans.toString();}public TreeNode deserialize(String data) {if (data == null) {return null;}String[] dataStr = data.split(",");List<Integer> dataList = Arrays.stream(dataStr).map(str -> str.equals("null") ? null : Integer.valueOf(str)).collect(Collectors.toList());Deque<TreeNode> queue = new LinkedList<>();TreeNode root = new TreeNode(dataList.get(0));queue.offer(root);int index = 1;for (; index < dataList.size(); index += 2) {TreeNode node = queue.poll();if (dataList.get(index) != null) {node.left = new TreeNode(dataList.get(index));queue.offer(node.left);}if (index + 1 < dataList.size() && dataList.get(index + 1) != null) {node.right = new TreeNode(dataList.get(index + 1));queue.offer(node.right);}}return root;} } -
解法二:DFS(前序遍历)
这里主要是通过前序遍历实现
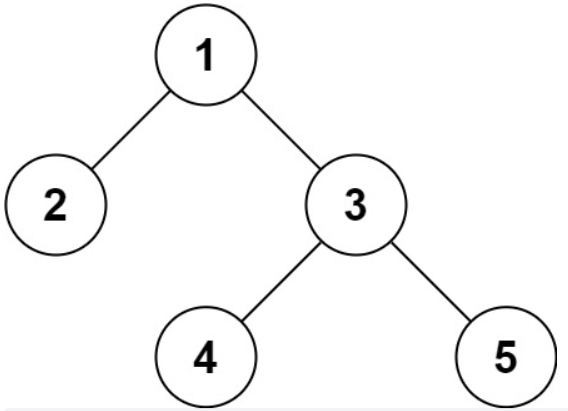
-
序列化实现比较简单,直接DFS搜索即可:
[1,2,null,null,3,4,null,null,5,null,null] -
反序列化的时候,第一个元素为根节点,接下来都是按照前序遍历的顺序,先走左边,直到遇到
null结束,然后换另一边
整个过程递归进行
class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) {val = x;} }/*** @author ghp* @title* @description*/ class Codec {public String serialize(TreeNode root) {StringBuilder ans = new StringBuilder();dfs(root, ans);ans.deleteCharAt(ans.length() - 1);return ans.toString();}private void dfs(TreeNode root, StringBuilder ans) {if (root == null) {ans.append("null,");return;}ans.append(root.val).append(",");dfs(root.left, ans);dfs(root.right, ans);}public TreeNode deserialize(String data) {String[] dataStr = data.split(",");// 根据前序遍历的结果构建二叉树return buildTree(dataStr);}private int i = 0;private TreeNode buildTree(String[] dataStr) {String value = dataStr[i++];if (value.equals("null")) {// 防止自动拆箱导致NPE,同时也是递归结束条件return null;}TreeNode node = new TreeNode(Integer.valueOf(value));// 构建左子树node.left = buildTree(dataStr);// 构建右子树node.right = buildTree(dataStr);return node;} }复杂度分析:
序列化
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( n ) O(n) O(n)
反序列化
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( n ) O(n) O(n)
其中 n n n 为二叉树节点的个数
-
最长递增子序列
🔒题目
原题链接:300.最长递增子序列
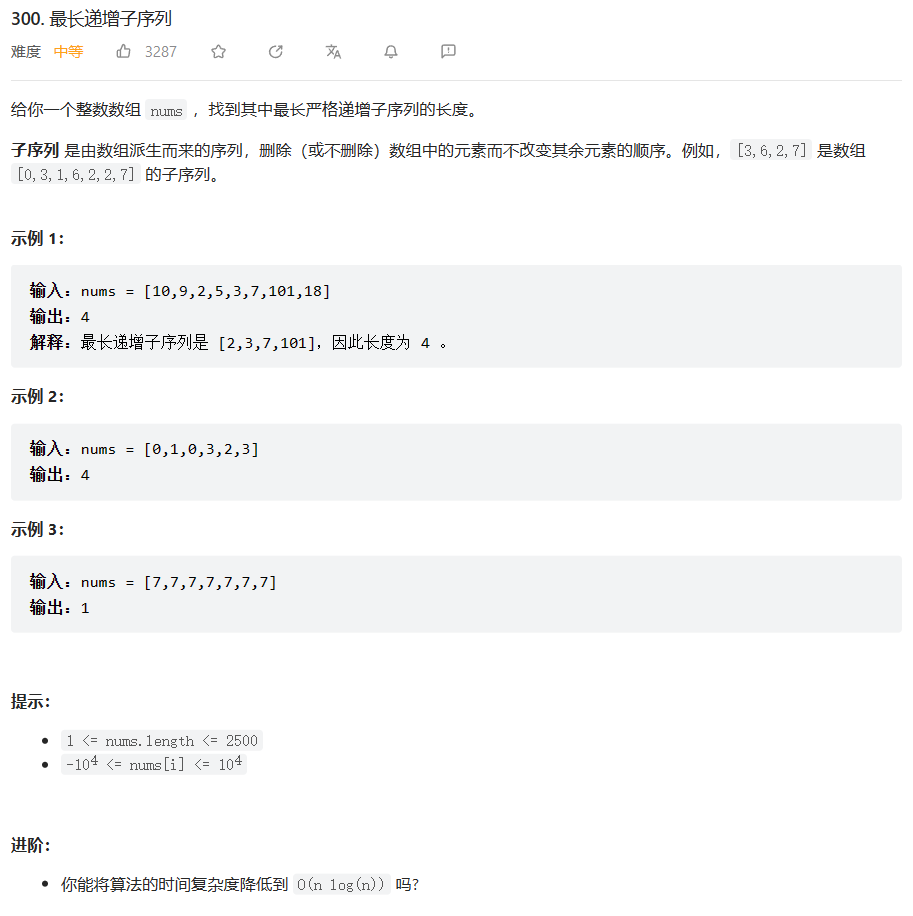
🔑题解
-
解法一:暴力DFS(超时 22 / 54)
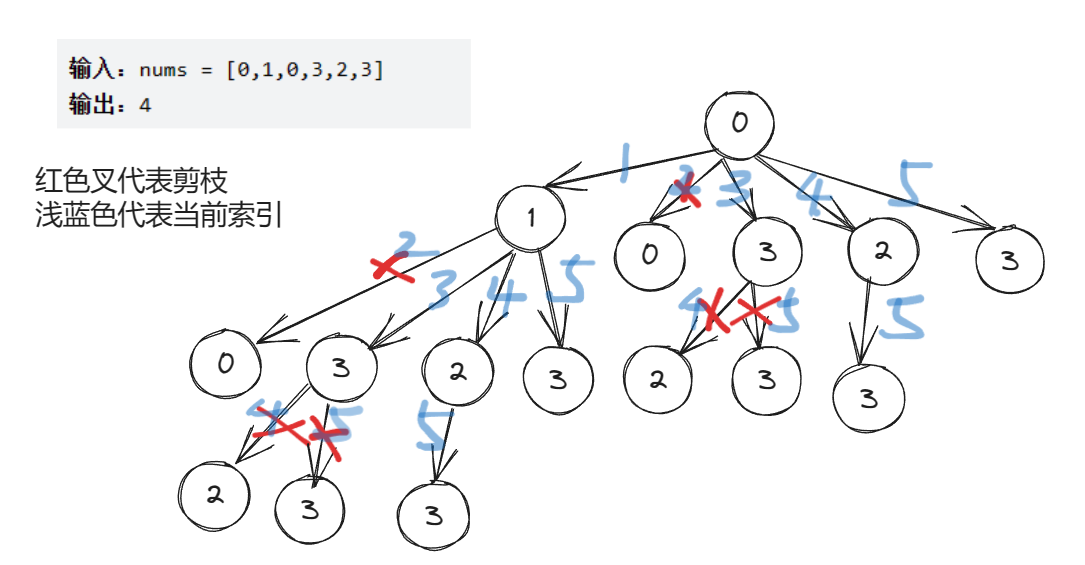
PS:画的有点丑,但是能看明白就行(●ˇ∀ˇ●)
/*** @author ghp* @title* @description*/ public class Solution {public int lengthOfLIS(int[] nums) {// 最长递增子序列的长度int maxLength = 0;// DFS遍历每一个节点for (int i = 0; i < nums.length; i++) {int length = dfs(nums, i, Integer.MIN_VALUE);maxLength = Math.max(maxLength, length);}return maxLength;}private int dfs(int[] nums, int index, int preLen) {if (index == nums.length) {// 达到数组末尾,返回长度为0return 0;}int len1 = 0;if (nums[index] > preLen) {// 当前元素大于前一个元素,可以选择当前元素作为递增子序列的一部分len1 = 1 + dfs(nums, index + 1, nums[index]);}// 不选择当前元素,继续寻找下一个递增子序列int len2 = dfs(nums, index + 1, preLen);// 返回选择当前元素和不选择当前元素中的较长子序列的长度return Math.max(len1, len2);} }复杂度分析:
- 时间复杂度: O ( 2 n ) O(2^n) O(2n),每一个节点都有选和不选两种情况,所以总的来说是 2 n 2^n 2n
- 空间复杂度: O ( l o g n ) O(logn) O(logn),空间复杂度为递归的最大深度,最大深度是树的最大高度
其中 n n n 为数组中元素的个数
代码优化:时间优化
我们可以通过记忆化搜索来大幅度提高搜索的速度,我们需要新增一个memo数组,
memo[i][j]表示以第i个元素为结尾、且第j个元素为上一个结尾元素的最长递增子序列的长度。为了新增一个记忆搜索功能,我们需要对上面代码进行一个微型改造,我们在DFS搜索时,不能像前面一样传递上一个节点的长度,而是需要传递上一个节点的索引,这样我们才能够使用memo数组对当前状态进行标记,下面的示意图是添加了记忆数组之后的搜索
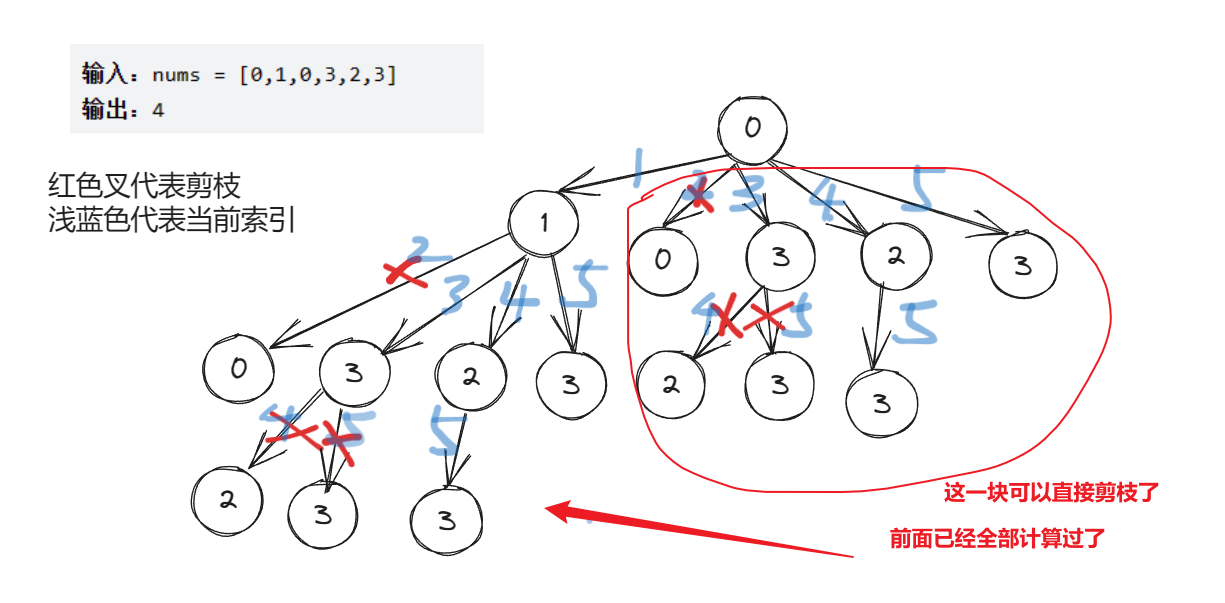
通过Debug也可以看出来,每进行一次DFS,都可以直接将当前节点到其它任意节点的距离计算出来,这样就能大幅度进行剪枝了。比如上图,0到1这条路径,就可以计算出0到其它节点(1,0,3,2,3)的距离了,后面的路径0到0、0到3、0到2、0到3就不用再去重新遍历了,而是直接拿我们缓存在memo中的路径
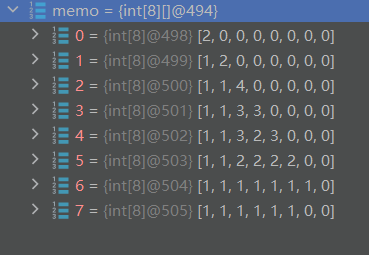
public class Solution {public int lengthOfLIS(int[] nums) {int maxLength = 1;// 记录节点的状态 memo[i][j]表示索引为j的节点到索引为i的节点的最长递增节点数int[][] memo = new int[nums.length][nums.length];// DFS搜索每一个节点for (int i = 0; i < nums.length; i++) {maxLength = Math.max(maxLength, dfs(nums, i, i, memo));}return maxLength;}private int dfs(int[] nums, int curIndex, int preIndex, int[][] memo) {if (curIndex >= nums.length) {// 后面已经没有节点了,结束搜索return 0;}if (memo[curIndex][preIndex] > 0) {// preIndex到curIndex这个状态已计算过,直接返回return memo[curIndex][preIndex];}int len1 = 0;if (preIndex == curIndex || nums[curIndex] > nums[preIndex]) {// 当前元素大于前一个元素,可以选择当前元素作为递增子序列的一部分len1 = 1 + dfs(nums, curIndex + 1, curIndex, memo);}// 不选择当前元素,继续寻找下一个递增子序列int len2 = dfs(nums, curIndex + 1, preIndex, memo);// 缓存preIndex到curIndex这个状态memo[curIndex][preIndex] = Math.max(len1, len2);// 返回选择当前元素和不选择当前元素中的较长子序列的长度return memo[curIndex][preIndex];} }记忆搜索是经典的拿时间换空间,时间复杂度虽然没有变,但是却大大缩减了搜索结果的时间,空间复杂度提高了
复杂度分析:
- 时间复杂度: O ( 2 n ) O(2^n) O(2n),每一个节点都有选和不选两种情况,所以总的来说是 2 n 2^n 2n
- 空间复杂度: O ( n 2 ) O(n^2) O(n2),memo占用 n 2 n^2 n2的空间
其中 n n n 为数组中元素的个数
备注:将
memo[curIndex][preIndex]转换为memo[preIndex][curIndex]是不可行的。这是因为preIndex的值是固定的,是遍历时的前一个索引,而curIndex是在不断递增变化的。如果我们将
memo[curIndex][preIndex]转换为memo[preIndex][curIndex],则无法正确存储和查找子问题的解决方案。由于curIndex不断增加,我们无法准确地映射到递归调用中的子问题。代码优化:空间优化
我们可以发现memo每进行一次DFS都只用到了一列的数据,所以我们完全可以将二维的memo压缩为一维的memo
public class Solution {public int lengthOfLIS(int[] nums) {int maxLength = 1;int[] memo = new int[nums.length];Arrays.fill(memo, 1);for (int i = 0; i < nums.length; i++) {maxLength = Math.max(maxLength, dfs(nums, i, memo));}return maxLength;}private int dfs(int[] nums, int curIndex, int[] memo) {if (curIndex >= nums.length) {return 0;}if (memo[curIndex] > 1) {return memo[curIndex];}int maxLen = 1;for (int i = curIndex + 1; i < nums.length; i++) {if (nums[i] > nums[curIndex]) {maxLen = Math.max(maxLen, 1 + dfs(nums, i, memo));}}memo[curIndex] = maxLen;return maxLen;} }复杂度分析:
- 时间复杂度: O ( n 2 ) O(n^2) O(n2),每一个节点都有选和不选两种情况,所以总的来说是 2 n 2^n 2n
- 空间复杂度: O ( n ) O(n) O(n),memo占用 n n n的空间
其中 n n n 为数组中元素的个数
-
解法二:动态规划
我们需要构建一个
dp[i],dp[i]表示以nums[i]结尾的最长递增子序列的长度,此时我们可以知道 当前第i个节点结尾的最长递增子序列,一定是由前面的节点转移而来的,至于是前面哪一个节点,我们无法直接确定,所以此时需要遍历 前面 i+1个节点,在遍历的同时,我们不断更新当前的dp[i],遍历完毕,即可得到当前最大长度。不知道为什么感觉动态规划比前面的DFS要简单多了
import java.util.Arrays;/*** @author ghp* @title* @description*/ public class Solution {public int lengthOfLIS(int[] nums) {if (nums.length == 0) {return 0;}int maxLength = 1;int[] dp = new int[nums.length];// 每一个节点自身的初始长度都是1Arrays.fill(dp, 1);// 遍历每一个节点for (int i = 1; i < nums.length; i++) {// 遍历0~i之间的节点,计算出所有以当前nums[i]结尾的最长递增子序列的长度for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) {dp[i] = Math.max(dp[i], dp[j] + 1);}}maxLength = Math.max(maxLength, dp[i]);}return maxLength;} }复杂度分析:
- 时间复杂度: O ( n 2 ) O(n^2) O(n2)
- 空间复杂度: O ( n ) O(n) O(n)
其中 n n n 为数组中元素的个数
-
解法三:动态规划+二分查找
来自:300. 最长递增子序列(动态规划 + 二分查找,清晰图解) - 最长递增子序列 - 力扣(LeetCode)
class Solution {public int lengthOfLIS(int[] nums) {int len = 1, n = nums.length;if (n == 0) {return 0;}int[] d = new int[n + 1];d[len] = nums[0];for (int i = 1; i < n; ++i) {if (nums[i] > d[len]) {d[++len] = nums[i];} else {int l = 1, r = len, pos = 0; // 如果找不到说明所有的数都比 nums[i] 大,此时要更新 d[1],所以这里将 pos 设为 0while (l <= r) {int mid = (l + r) >> 1;if (d[mid] < nums[i]) {pos = mid;l = mid + 1;} else {r = mid - 1;}}d[pos + 1] = nums[i];}}return len;} }作者:LeetCode-Solution 链接:https://leetcode.cn/problems/longest-increasing-subsequence/solution/zui-chang-shang-sheng-zi-xu-lie-by-leetcode-soluti/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。复杂度分析:
- 时间复杂度: O ( n l o g n ) O(nlogn) O(nlogn)
- 空间复杂度: O ( n ) O(n) O(n)
其中 n n n 为数组中元素的个数
删除无效括号
先缓缓w(゚Д゚)w,明天在写把,不然今天任务完不成了
🔒题目
原题链接:301.删除无效括号
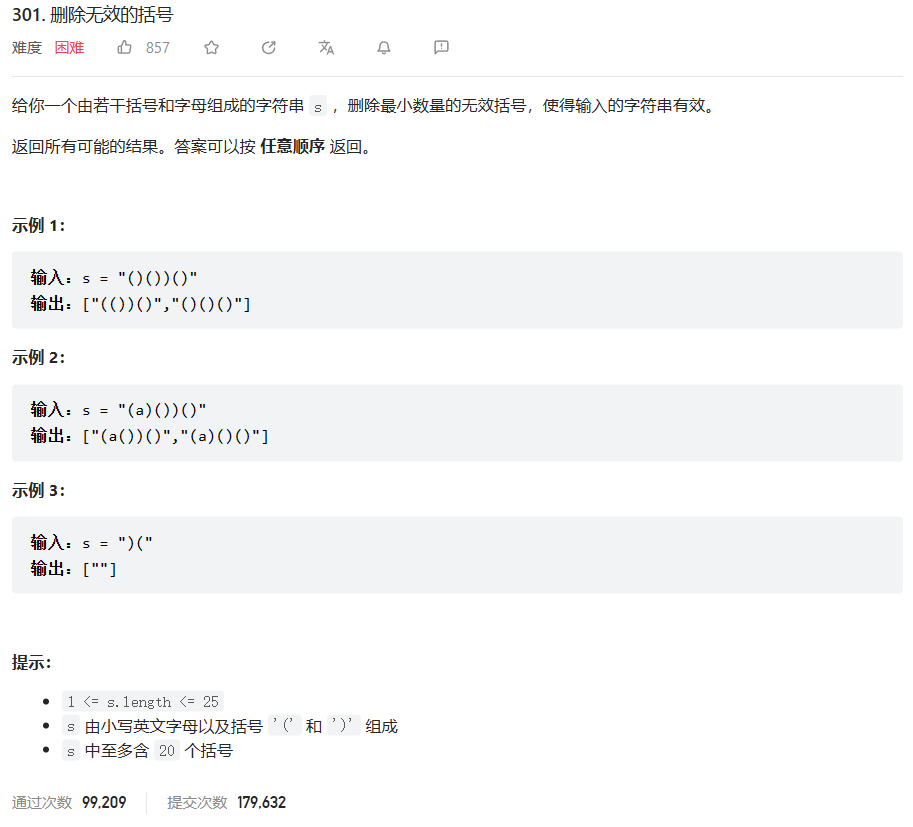
🔑题解
-
解法一:暴力
复杂度分析:
- 时间复杂度: O ( n 2 ) O(n^2) O(n2)
- 空间复杂度: O ( 1 ) O(1) O(1)
其中 n n n 为数组中元素的个数
-
解法二:哈希表
这个太强了,时间复杂度直接变成 O ( n ) O(n) O(n),它是利用Map的Key不能重复的特性,来判断元素是否符合要求。
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( n ) O(n) O(n)
其中 n n n 为数组中元素的个数
参考题解:
- 9种方法(可能是目前最全的),拓展大家思路 - 寻找重复数 - 力扣(LeetCode)
- 使用「二分查找」搜索一个有范围的整数(结合「抽屉原理」) - 寻找重复数 - 力扣(LeetCode)
- 【图解】dfs + bfs + 后序遍历 + 其他思路 - 二叉树的序列化与反序列化 - 力扣(LeetCode)# 【LeetCode热题100】打卡第44天:倒数第30~25题
相关文章:

【LeetCode热题100】打卡第44天:倒数第30~25题
文章目录 【LeetCode热题100】打卡第44天:倒数第30~25题⛅前言 移动零🔒题目🔑题解 寻找重复数🔒题目🔑题解 二叉树的序列化与反序列化🔒题目🔑题解 最长递增子序列🔒题目ǵ…...

C# 匿名方法和Lambda表达式
一.匿名方法 1.匿名方法的演变 匿名方法是为了简化委托的实现,方便调用委托方法而出现的,同时,匿名方法也是学好lambda表达式的基础。在委托调用的方法中,如果方法只被调用一次,这个时候我们就没有必要创建具名方法&…...

uniapp微信小程序scroll-view滚动scrollLeft不准确
今天在实现微信小程序的一个横向导航的时候出现了一个问题,就是每次滑到滚动条最右边的时候 scrollLeft的值都不准确 原因:因为每次滚动监听事件都会被调用比较耗费资源系统会默认节流,可以在scroll-view 加一个 throttle“{{false}}” 关闭…...

symfony/console
github地址:GitHub - symfony/console: Eases the creation of beautiful and testable command line interfaces 文档地址:The Console Component (Symfony 5.4 Docs) 默认命令list,可以用register注册一个command命令,之后可以…...
OSI模型简介及socket,tcp,http三者之间的区别和原理
1.OSI模型简介(七层网络模型) OSI 模型(Open System Interconnection model):一个由国际标准化组织提出的概念模型,试图提供一个使各种不同的计算机和网络在世界范围内实现互联的标准框架。 它将计算机网络体系结构划分为七层,每…...

【leetcode】leetcode69 x的平方根
文章目录 给你一个非负整数 x ,计算并返回 x 的 算术平方根 。原理牛顿法(数值分析中使用到的):二分法 解决方案java 实现实例执行结果 python 实现实例 给你一个非负整数 x ,计算并返回 x 的 算术平方根 。 由于返回类型是整数&…...
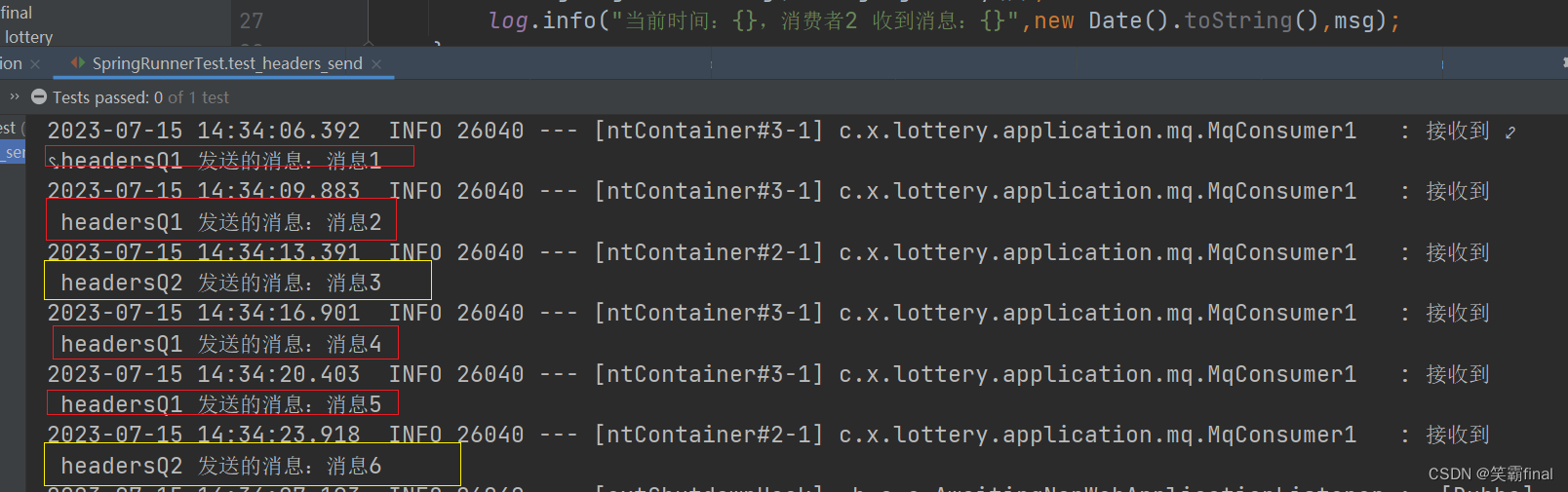
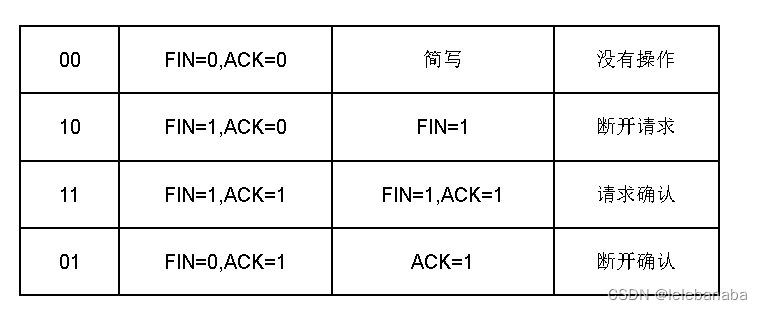
springboot与rabbitmq的整合【演示5种基本交换机】
前言: 👏作者简介:我是笑霸final,一名热爱技术的在校学生。 📝个人主页:个人主页1 || 笑霸final的主页2 📕系列专栏:后端专栏 📧如果文章知识点有错误的地方,…...

【设计模式】设计原则-单一职责原则
单一职责原则 类的设计原则之单一职责原则,是最常用的类的设计的原则之一。 百度百科:就一个类而言,应该仅有一个引起它变化的原因。应该只有一个职责。 通俗的讲就是:一个类只做一件事 这个解释更通俗易懂,也更符…...

【C++】-多态的底层原理
💖作者:小树苗渴望变成参天大树🎈 🎉作者宣言:认真写好每一篇博客💤 🎊作者gitee:gitee✨ 💞作者专栏:C语言,数据结构初阶,Linux,C 动态规划算法🎄 如 果 你 …...
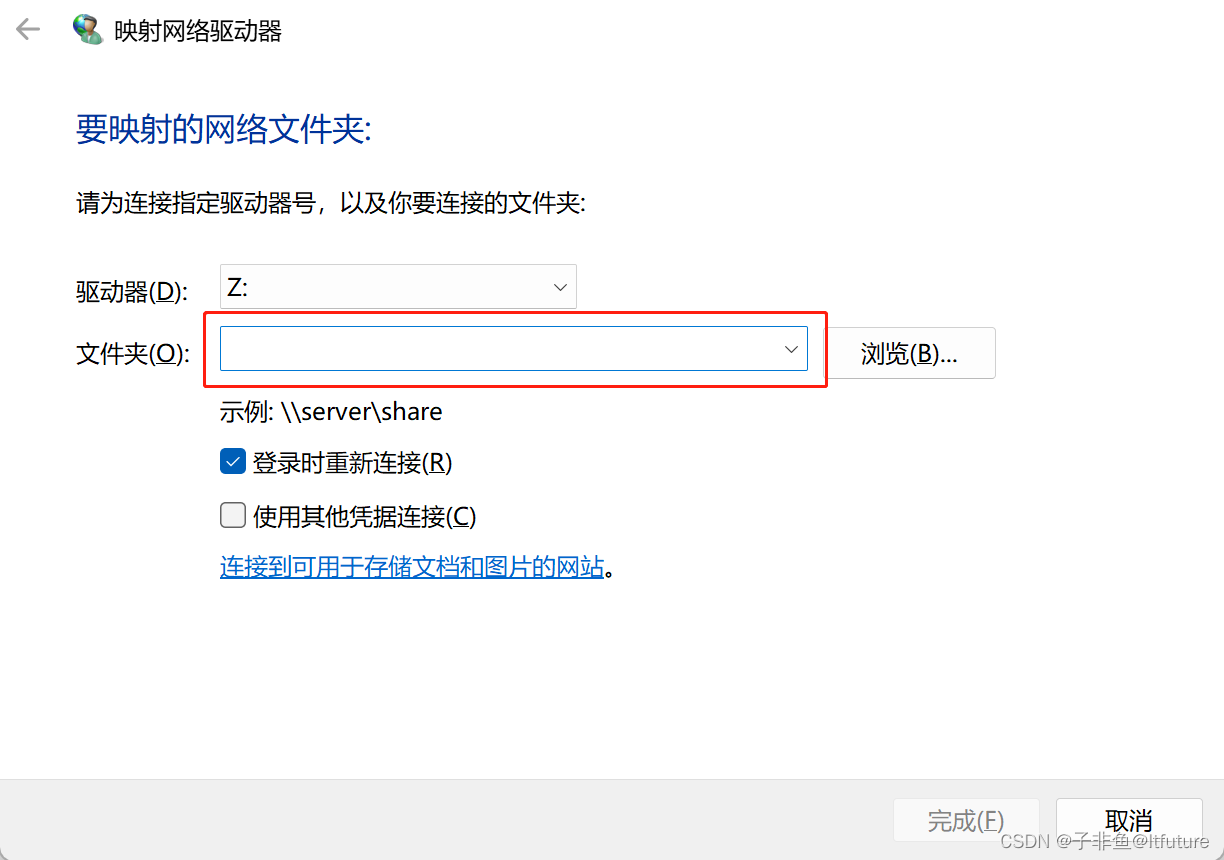
【部署】让你的电脑多出一个磁盘来用!使用SSHFS将远程服务器目录挂载到Windows本地,挂载并共享服务器资源
让你的电脑多出一个磁盘来用!---使用SSHFS将远程服务器目录挂载到Windows本地 1. 方法原理介绍2.SSHFS-Win使用教程—实现远程服务器磁盘挂载本地 由于日常主要用 Windows 系统,每次都得 ssh 到服务器上进行取资源(本地磁盘不富裕)…...
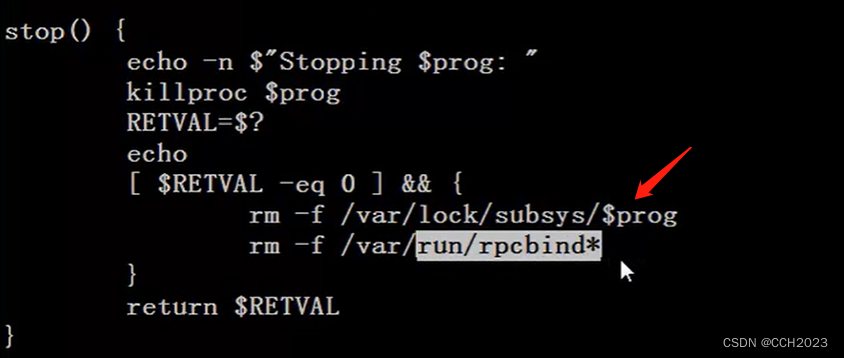
/var/lock/subsys目录的作用
总的来说,系统关闭的过程(发出关闭信号,调用服务自身的进程)中会检查/var/lock/subsys下的文件,逐一关闭每个服务,如果某一运行的服务在/var/lock/subsys下没有相应的选项。在系统关闭的时候,会…...

DETR (DEtection TRansformer)基于自建数据集开发构建目标检测模型超详细教程
目标检测系列的算法模型可以说是五花八门,不同的系列有不同的理论依据,DETR的亮点在于它是完全端到端的第一个目标检测模型,DETR(Detection Transformer)是一种基于Transformer的目标检测模型,由Facebook A…...

C++初阶 - 5.C/C++内存管理
目录 1.C/C的内存分布 2.C语言中动态内存管理方式:malloc、calloc、realloc、free 3.C内存管理方式 3.1 new/delete操作内置类型 3.2 new 和 delete操作自定义类型 4.operator new 与 operator delete 函数(重要点) 4.1 operator new 与…...

数学建模学习(3):综合评价类问题整体解析及分析步骤
一、评价类算法的简介 对物体进行评价,用具体的分值评价它们的优劣 选这两人其中之一当男朋友,你会选谁? 不同维度的权重会产生不同的结果 所以找到每个维度的权重是最核心的问题 0.25 二、评价前的数据处理 供应商ID 可靠性 指标2 指…...
 | 限流:濒临奔溃?限流守护者拯救系统于水火之中!)
【后端面经】微服务构架 (1-5) | 限流:濒临奔溃?限流守护者拯救系统于水火之中!
文章目录 一、前置知识1、什么是限流?2、限流算法A) 静态算法a) 漏桶b) 令牌桶c) 固定窗口d) 滑动窗口B) 动态算法3、限流的模式4、 限流对象4、限流后应该怎么做?二、面试环节1、面试准备2、基本思路3、亮点展现A) 突发流量(针对请求个数而言)B) 请求大小(针对请求大小而言)…...

HDFS异构存储详解
异构存储 HDFS异构存储类型什么是异构存储异构存储类型如何让HDFS知道集群中的数据存储目录是那种类型存储介质 块存储选择策略选择策略说明选择策略的命令 案例:冷热温数据异构存储对应步骤 HDFS内存存储策略支持-- LAZY PERSIST介绍执行使用 HDFS异构存储类型 冷…...

《面试1v1》Kafka消息是采用Pull还是Push模式
🍅 作者简介:王哥,CSDN2022博客总榜Top100🏆、博客专家💪 🍅 技术交流:定期更新Java硬核干货,不定期送书活动 🍅 王哥多年工作总结:Java学习路线总结…...

Windows环境Docker安装
目录 安装Docker Desktop的步骤 Docker Desktop 更新WSL WSL 的手动安装步骤 Windows PowerShell 拉取(Pull)镜像 查看已下载的镜像 输出"Hello Docker!" Docker Desktop是Docker官方提供的用于Windows的图形化桌面应用程序,…...
: singleton类型的bean和prototype类型的bean协同工作的方法(二))
Spring 6.0官方文档示例(23): singleton类型的bean和prototype类型的bean协同工作的方法(二)
使用lookup-method: 一、实体类: package cn.edu.tju.domain2;import java.time.LocalDateTime; import java.util.Map;public class Command {private Map<String, Object> state;public Map<String, Object> getState() {return state;}public void …...
Docker Compose 容器编排
Docker compose Docker compose 实现单机容器集群编排管理(使用一个模板文件定义多个应用容器的启动参数和依赖关系,并使用docker compose来根据这个模板文件的配置来启动容器) 通俗来说就是把之前的多条docker run启动容器命令 转换为docker…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
