【C# 数据结构】Heap 堆
【C# 数据结构】Heap 堆
- 先看看C#中有那些常用的结构
- 堆的介绍
- 完全二叉树
- 最大堆
- Heap对类进行排序
- 实现 `IComparable<T>` 接口
- 对CompareTo的一点解释
- 参考资料
先看看C#中有那些常用的结构
作为 数据结构系类文章 的开篇文章,我们先了解一下C# 有哪些常用的数据结构
C# 是一种通用、面向对象的编程语言,它提供了许多常用的数据结构,以便在开发过程中高效地存储和操作数据。以下是一些在 C# 中常用的数据结构:
-
数组 (Array):
数组是一个固定大小的、相同类型元素的集合。使用索引来访问数组中的元素。 -
列表 (List):
列表是一个动态大小的集合,可以根据需要自动增长或缩小。List 是泛型类,T 表示可以存储的元素类型。 -
链表 (LinkedList):
链表是一种数据结构,其中的元素按节点 (Node) 连接在一起,每个节点包含一个数据元素和一个指向下一个节点的引用。 -
栈 (Stack):
栈是一种后进先出 (Last-In-First-Out, LIFO) 的数据结构,只允许在顶部插入和删除元素。 -
队列 (Queue):
队列是一种先进先出 (First-In-First-Out, FIFO) 的数据结构,允许在一端插入元素,在另一端删除元素。 -
字典 (Dictionary):
字典是一种键值对 (Key-Value) 映射的集合,允许通过键来快速查找和访问值。 -
散列表 (HashSet, Hashtable):
散列表是一种根据键快速查找值的数据结构。HashSet 是一个泛型类,而 Hashtable 是非泛型的旧式实现。 -
堆 (Heap):
堆是一种特殊的树状数据结构,其中的每个节点的值都大于或小于其子节点的值。常用于优先队列等场景。 -
树 (Tree):
树是一种分层数据结构,其中的节点以层次结构进行组织。常见的树包括二叉树、二叉搜索树等。 -
图 (Graph):
图是一组节点和边的集合,用于表示各种复杂关系。常见的图算法包括深度优先搜索和广度优先搜索。
ps: 我们经常说堆栈堆栈,其实这样一看发现堆和栈的数据结构是完全不同的。
堆的介绍
完全二叉树
堆首先是个树状的结构,而且是个完全二叉树!什么是完全二叉树?
完全二叉树:二叉树除了最后一层节点外,其他层的节点个数必须是最大值,如果最后一层没有达到最大节点,则所有的节点必须偏向左边。
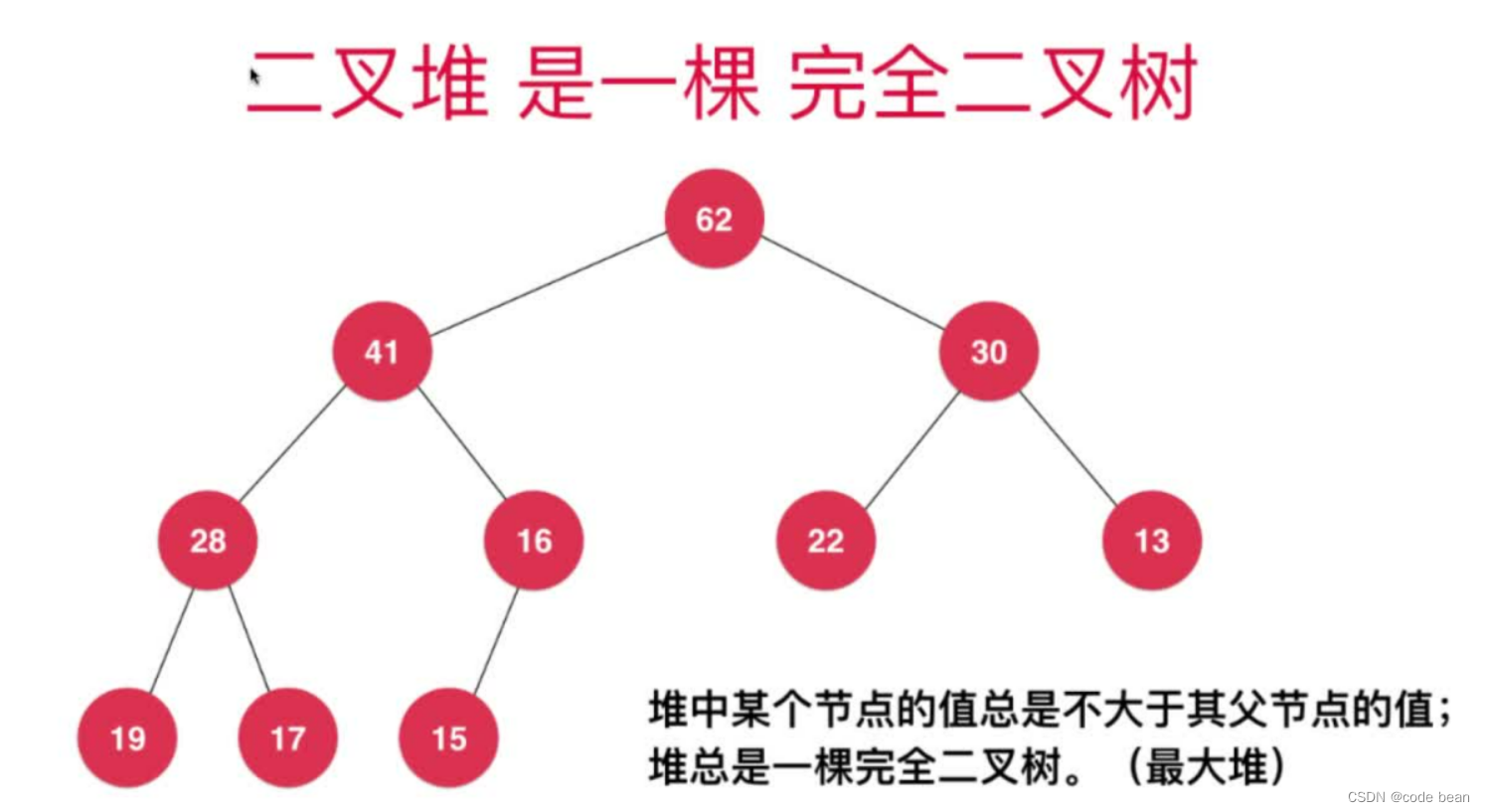
如何理解:其他层的节点个数必须是最大值?
就是第一层 一个节点,第二层 两个节点 第三层 四个节点,以此类推。
不过最后一层不要求节点个数是最大值。(最后一层没有达到最大节点,则所有的节点必须偏向左边)
那这个完全二叉树的定义有啥用了,为啥搞这么多规矩出来?
那是因为完全二叉树这样个树的结构,是可以通过数值存储的!(因为其节点的位置在数组中的索引之间有一种固定的关系)
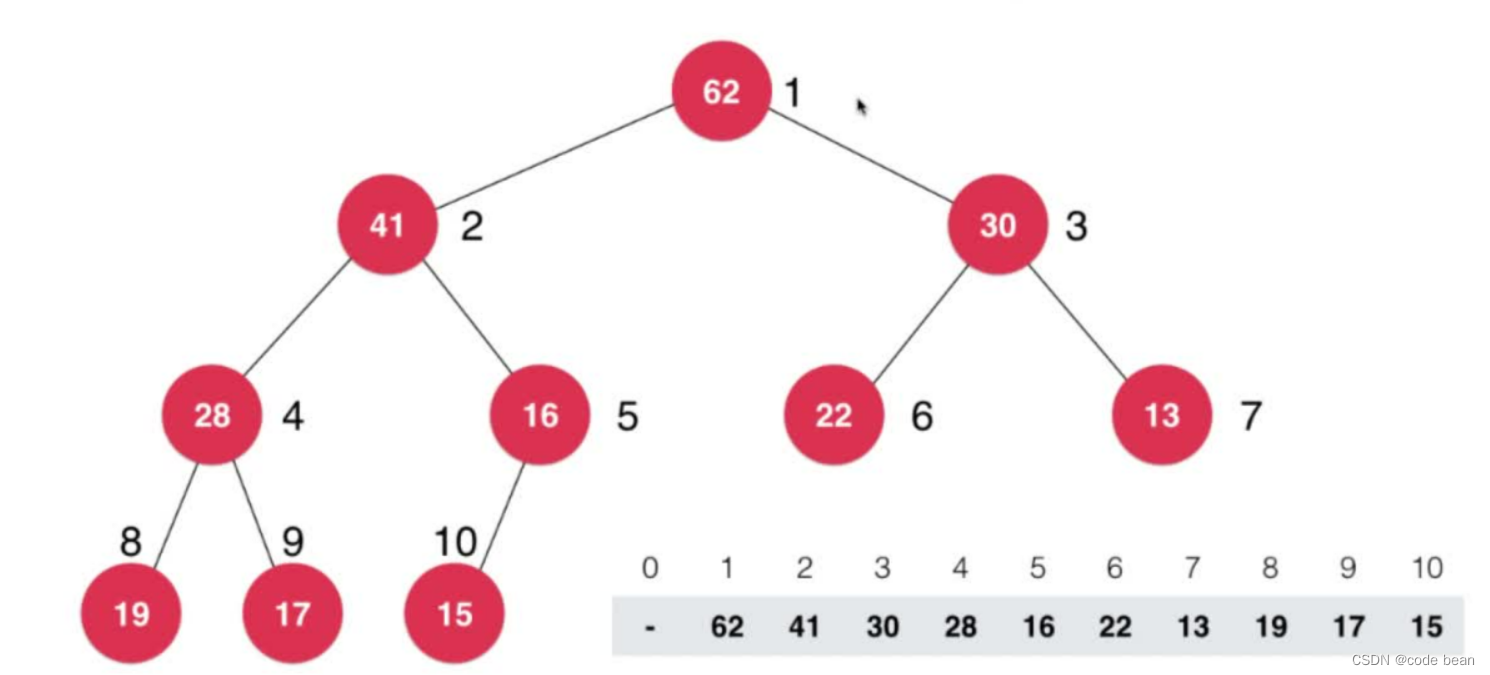
前提:数据的0号地址不使用,从1开始使用。
如果将完全二叉树从上到下、从左到右依次编号,那么节点 i 的左子节点索引为 2i,右子节点索引为 2i+1,父节点索引为 i/2(注意这里除法是计算机里整除的意思)
当然二叉树还要其他特点这里了解即可:
完美填充:完全二叉树是按照从左到右的顺序填充节点的,除了最后一层外,其他层的节点都是满的(即每个节点都有两个子节点)。最后一层的节点从左到右填充,可能是满的,也可能是部分填充,但是最后一层的节点一定是从左到右依次填充的,不会有空洞。
叶节点:所有叶节点都集中在最后一层或者倒数第二层。如果最后一层的叶节点没有填满,则它们一定是从左到右依次连续排列的。
层数:完全二叉树的层数为 h,从根节点到倒数第二层都是满的,最后一层可能不满。因此,节点总数 N 满足 N = 2^h - 1 + 最后一层节点数。
高度平衡:由于完全二叉树的特点,其左右子树的高度差不会超过 1,因此是一个高度平衡的二叉树。
最大堆
首先最大堆,必须是完全二叉树
每一个节点可以有两个子节点。任何一个节点都不不大于他的父节点
那么最大堆,树顶的位置是最大的元素
有最大堆就有最小堆:
最小堆:树顶的位置是最小的元素(堆中某个节点的值总是不小于其父节点的值)
C# 中的 Heap 实际上是最小堆(Min Heap)的实现,其中最小的元素总是位于堆的顶部。
在 C# 中,可以使用 System.Collections.Generic 命名空间中的 Heap 数据结构来实现堆(Heap)。Heap 通常用于实现优先队列等场景,其中每个元素都有一个优先级(或者键值),并且可以根据优先级高低进行插入和删除操作。
下面是如何使用 Heap 数据结构的基本步骤:
Step 1: 导入命名空间
首先,在代码文件中导入 System.Collections.Generic 命名空间,以便可以使用 Heap 类。
using System.Collections.Generic;
Step 2: 创建 Heap
使用 Heap 类创建一个堆对象。Heap 类是一个泛型类,你需要指定元素的类型。以下是一个示例创建最小堆的代码:
Heap<int> minHeap = new Heap<int>();
Step 3: 插入元素
使用 Insert 方法将元素插入堆中。插入元素后,堆会自动调整,以确保最小元素位于堆的顶部。
minHeap.Insert(10);
minHeap.Insert(5);
minHeap.Insert(15);
minHeap.Insert(3);
// 此时堆为:3 5 15 10
Step 4: 获取堆顶元素
使用 Peek 方法获取堆顶(最小)元素,但不删除它。
int minValue = minHeap.Peek();
// minValue 等于 3
// 此时堆仍为:3 5 15 10
Step 5: 弹出堆顶元素
使用 ExtractMin 方法弹出堆顶元素(即删除堆顶最小元素),并返回该元素的值。
int minValue = minHeap.ExtractMin();
// minValue 等于 3,同时堆变为:5 10 15
看到这里我们知道堆的作用其实就是优先级排序,比如计算机任务,每个任务都会有一个优先级,优先级高的任务被先处理,而且随时还可能来新的任务。 那我们为何要使用对进行排序呢?
那是因为每次来新任务时,就需要重新排序,如果是普通的排序,计算量是非常大的:

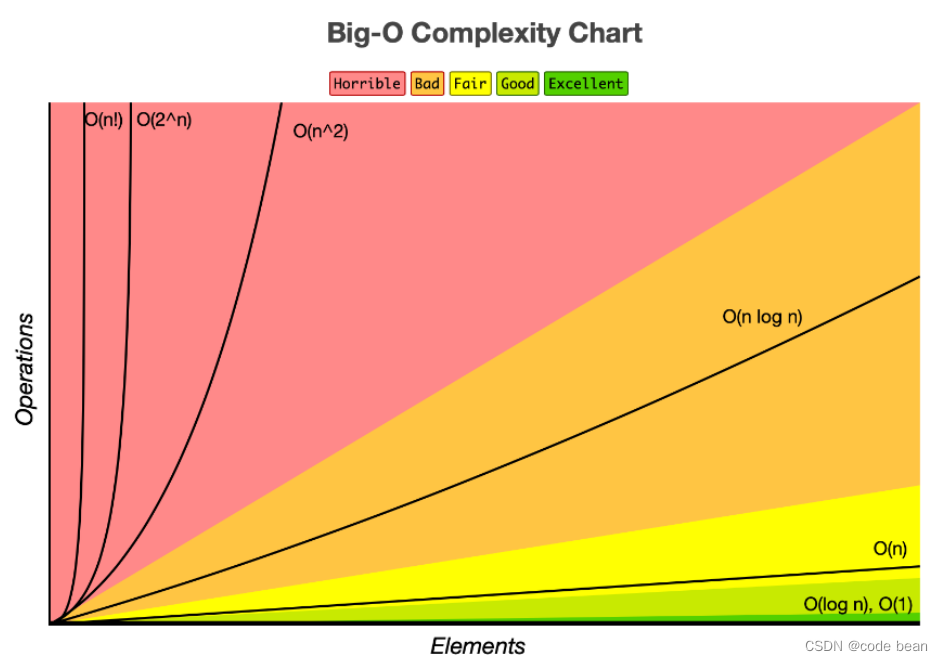
也就是说堆在实现优先级排序的时候是最合适的。
至于如何自己写代码实现一个堆,这里就不说了,继续介绍实际中会直接用到的。
现在假设我有一个类,而不是int这样的数组,我们怎么用堆排序呢?
Heap对类进行排序
当你有一个自定义的类,想要在 Heap 中根据类的某个属性来表示优先级时,你可以通过实现 IComparable<T> 接口或者自定义比较器来实现。
假设你有一个名为 MyClass 的类,其中包含一个整数属性 Priority 用于表示优先级,那么你可以按照以下两种方法之一来使用 Heap<MyClass> 并根据 Priority 属性来表示优先级:
实现 IComparable<T> 接口
让 MyClass 类实现 IComparable<T> 接口,并在 CompareTo 方法中定义对象之间的优先级比较逻辑。
using System;
using System.Collections.Generic;public class MyClass : IComparable<MyClass>
{public int Priority { get; set; }public string Data { get; set; }// 实现 IComparable<T> 接口中的 CompareTo 方法public int CompareTo(MyClass other){return Priority.CompareTo(other.Priority);}
}// 创建最小堆,根据 MyClass 的优先级属性进行比较
Heap<MyClass> minHeap = new Heap<MyClass>();// 添加 MyClass 对象到最小堆
minHeap.Insert(new MyClass { Priority = 10, Data = "Value1" });
minHeap.Insert(new MyClass { Priority = 5, Data = "Value2" });
minHeap.Insert(new MyClass { Priority = 15, Data = "Value3" });
minHeap.Insert(new MyClass { Priority = 3, Data = "Value4" });// 弹出堆顶元素(优先级最小的对象)
while (minHeap.Count > 0)
{MyClass minPriorityObj = minHeap.ExtractMin();Console.WriteLine($"Priority: {minPriorityObj.Priority}, Value: {minPriorityObj.Data}");
}
这种方法都允许你在 Heap<MyClass> 中根据 Priority 属性来表示对象的优先级,并按优先级顺序插入和弹出对象。
对CompareTo的一点解释
有些童鞋对这里可能有的不明白,这里稍微解释一下
public int CompareTo(MyClass other)
{return Priority.CompareTo(other.Priority);
}
首先,C# 有跟多类实现了 实现 IComparable 接口中的 CompareTo 方法
用于比较对象之间的大小关系。这些类实现了 IComparable<T> 接口,以允许在容器中进行自定义排序。以下是一些常见的实现了 CompareTo 方法的类:
-
Int32、Int64、Single、Double、Decimal等数值类型:这些数值类型都实现了IComparable<T>接口,使得它们可以通过CompareTo方法进行比较。 -
DateTime类:DateTime类也实现了IComparable<T>接口,因此你可以使用CompareTo方法来比较日期和时间的大小。 -
String类:String类实现了IComparable<T>接口,允许你比较字符串的大小关系。它使用基于 Unicode 编码的排序规则。 -
TimeSpan类:TimeSpan类实现了IComparable<T>接口,允许你比较时间间隔的大小关系。 -
Enum枚举类型:枚举类型实现了IComparable<T>接口,使得枚举值之间可以通过CompareTo方法进行比较。 -
Version类:Version类用于表示软件版本号,它实现了IComparable<T>接口,允许你比较软件版本的大小关系。
x.Priority.CompareTo(y.Priority) 是一个比较表达式,用于比较两个对象 x 和 y 的 Priority 属性的值。它会返回一个整数,指示这两个值之间的关系。
具体含义如下:
- 如果
x.Priority小于y.Priority,则表达式返回负数(通常为-1)。 - 如果
x.Priority等于y.Priority,则表达式返回零。 - 如果
x.Priority大于y.Priority,则表达式返回正数(通常为1)。
这个返回值在使用自定义比较器或实现 IComparable<T> 接口时非常重要,因为它将用于决定如何排序或比较两个对象。根据返回值的正负,容器(如 Heap、List 等)会根据你定义的比较逻辑来确定对象的排序顺序。
例如,在上述代码中,我们使用了这个比较表达式来定义 MyClass 对象之间的优先级比较逻辑。在最小堆中,这个比较表达式的结果将决定 MyClass 对象的排序顺序,使得具有较小 Priority 属性值的对象排在堆顶,而具有较大 Priority 属性值的对象排在堆底。
所以,返回值的含义非常简单,它指示了两个对象之间的大小关系,用于实现排序和比较。
参考资料
https://coding.imooc.com/class/71.html
相关文章:

【C# 数据结构】Heap 堆
【C# 数据结构】Heap 堆 先看看C#中有那些常用的结构堆的介绍完全二叉树最大堆 Heap对类进行排序实现 IComparable<T> 接口 对CompareTo的一点解释 参考资料 先看看C#中有那些常用的结构 作为 数据结构系类文章 的开篇文章,我们先了解一下C# 有哪些常用的数据…...

智慧园区楼宇合集:数字孪生管控系统
智慧园区是指将物联网、大数据、人工智能等技术应用于传统建筑和基础设施,以实现对园区的全面监控、管理和服务的一种建筑形态。通过将园区内设备、设施和系统联网,实现数据的传输、共享和响应,提高园区的管理效率和运营效益,为居…...

Ajax 黑马学习
Ajax 资源 数据是服务器对外提供的资源,通过 请求 - 处理 - 响应方式获取 请求服务器数据, 用到 XMLHttpRequest 对象 XMLHttpRequest 是浏览器提供的js成员, 通过它可以请求服务器上的数据资源 let xmlHttpRequest new XMLHttpRequest(); 请求方式 : get向服务器获取数据…...

软件应用开发的常见环境
一般来说,在小型项目中可能只有开发环境和生产环境;在中型项目中会有开发环境、staging environment、生产环境;在大型项目中会有开发环境、测试环境、staging environment、生产环境。 一、Dev Env / Development Environment 开发环境 开…...
, into_iter(), iter_mut())
Rust中的iter(), into_iter(), iter_mut()
在Rust中,iter(), into_iter(), iter_mut()都是用于在集合类型上创建迭代器的方法。这三个方法各有不同,下面一一进行介绍。 iter(): iter() 方法创建一个不可变的引用迭代器。当你只想读取集合中的元素,而不想改变它们或消耗集合时ÿ…...

[SQL挖掘机] - 日期函数 - current_date
current_date函数时,它通常被用来获取当前的日期。它返回一个表示当前日期的日期值。 current_date函数没有任何参数,因此只需简单地调用它即可获得系统当前日期。 以下是一个示例: select current_date;这将返回当前日期,例如…...

JAVA面试总结-Redis篇章(三)——缓存雪崩
JAVA面试总结-Redis篇章(三)——缓存雪崩...
maven编译报错
参考链接:mvn打包No compiler is provided in this environment. Perhaps you are running on a JRE rather than a JDK_51CTO博客_mvn打包命令 在执行 yum install -y java-1.8.0-opensdk命令后,使用maven去编译打包,结果报错, …...

HPC集群调度系统和计算系统
什么是计算云? 所谓的计算云指的是为计算业务优化的类云基础架构,它强调用云的方式解决计算问题,而不是将“计算”搬到现有的公有云或者容器云上。 目前公有云或者容器云(例如k8s)上的HPC解决方案本质上都是将现有的H…...

pg_archivecleanup清理wal日志
一、 注意事项 pg_archivecleanup代码中仅进行了wal日志文件名的对比,没有实现对WAL日志名及对应生成时间的判断。在WAL日志未被重命名时,时间与日志名顺序名一致,没有问题。一旦WAL日志被重命名,pg_archivecleanup清理就可能清理…...
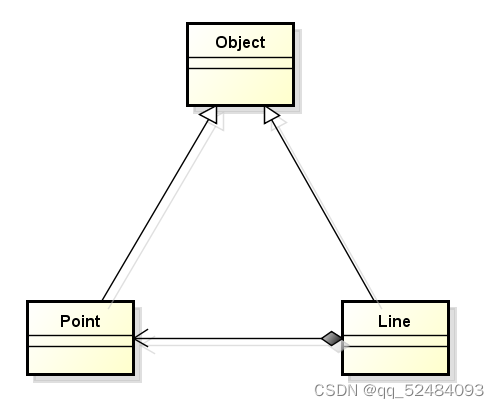
继承中的访问级别
值得思考的问题 子类是否可以直接访问父类的私有成员? 思考过程 继承中的访问级别 面向对象中的访问级别不止是 public 和 private 可以定义 protected 访问级别 关键字 protected 的意义 修饰的成员不能被外界直接访问修饰的成员可以被子类直接访问 思考 为什…...
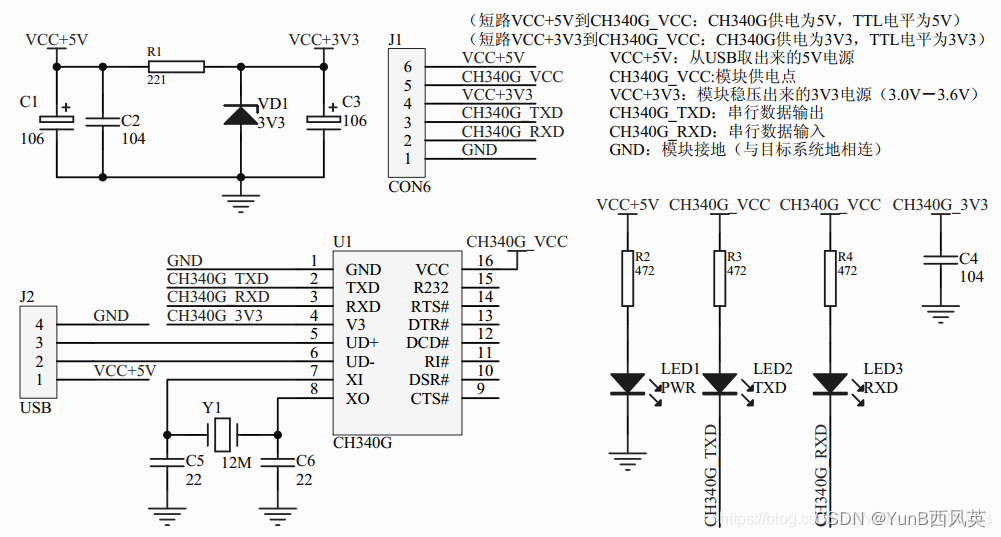
(学习日记)2023.06.09
写在前面: 由于时间的不足与学习的碎片化,写博客变得有些奢侈。 但是对于记录学习(忘了以后能快速复习)的渴望一天天变得强烈。 既然如此 不如以天为单位,以时间为顺序,仅仅将博客当做一个知识学习的目录&a…...

激光雷达-相机联合标定
https://f.daixianiu.cn/csdn/9499401684344864.html ros usb相机内参标定 ROS系统-摄像头标定camera calibration_berry丶的博客-CSDN博客...
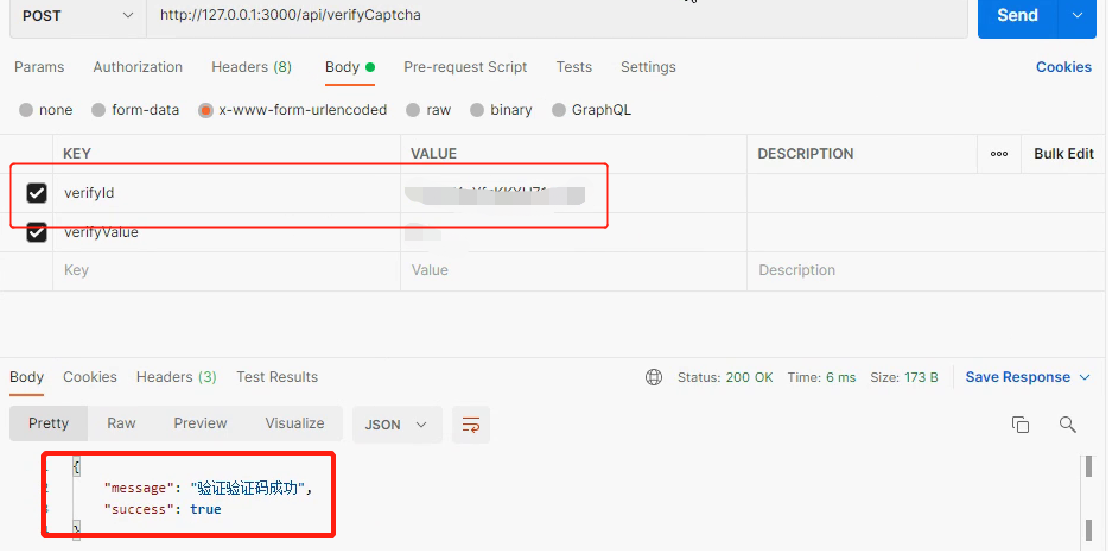
[golang gin框架] 40.Gin商城项目-微服务实战之Captcha验证码微服务
本次内容需要 gin框架基础知识, golang微服务基础知识才能更好理解 一.Captcha验证码功能引入 在前面,讲解了微服务的架构等,这里,来讲解前面商城项目的 Captcha验证码 微服务 ,captcha验证码功能在前台,后端 都要用到 ,可以把它 抽离出来 ,做成微服务功能 编辑 这个验证码功能…...
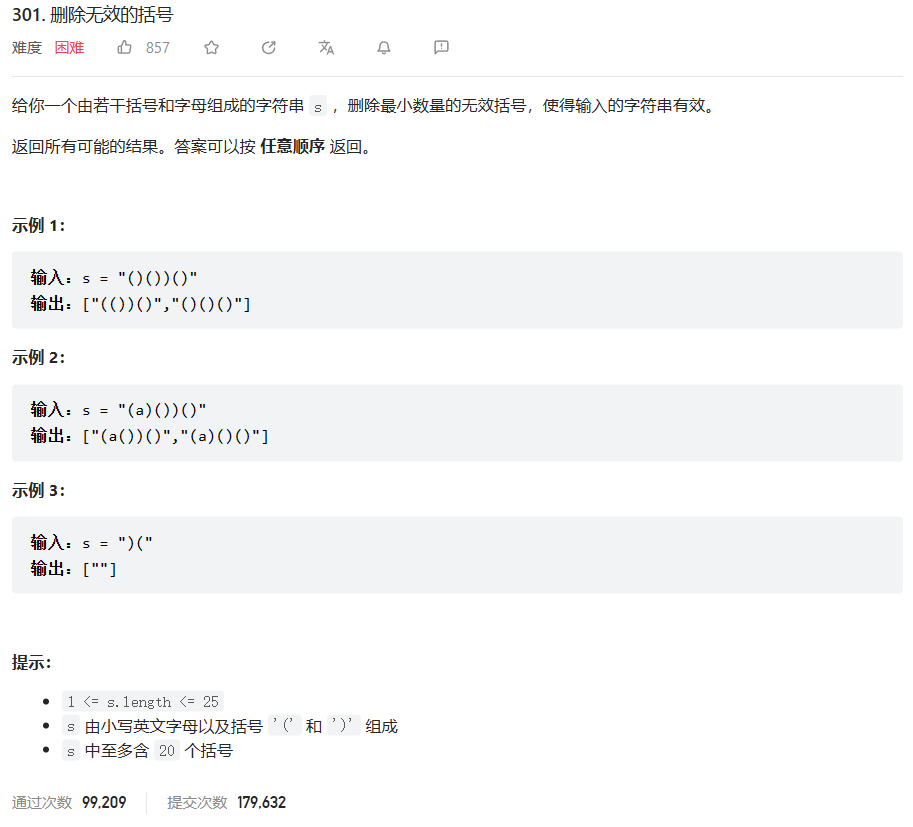
【LeetCode热题100】打卡第44天:倒数第30~25题
文章目录 【LeetCode热题100】打卡第44天:倒数第30~25题⛅前言 移动零🔒题目🔑题解 寻找重复数🔒题目🔑题解 二叉树的序列化与反序列化🔒题目🔑题解 最长递增子序列🔒题目ǵ…...

C# 匿名方法和Lambda表达式
一.匿名方法 1.匿名方法的演变 匿名方法是为了简化委托的实现,方便调用委托方法而出现的,同时,匿名方法也是学好lambda表达式的基础。在委托调用的方法中,如果方法只被调用一次,这个时候我们就没有必要创建具名方法&…...

uniapp微信小程序scroll-view滚动scrollLeft不准确
今天在实现微信小程序的一个横向导航的时候出现了一个问题,就是每次滑到滚动条最右边的时候 scrollLeft的值都不准确 原因:因为每次滚动监听事件都会被调用比较耗费资源系统会默认节流,可以在scroll-view 加一个 throttle“{{false}}” 关闭…...

symfony/console
github地址:GitHub - symfony/console: Eases the creation of beautiful and testable command line interfaces 文档地址:The Console Component (Symfony 5.4 Docs) 默认命令list,可以用register注册一个command命令,之后可以…...
OSI模型简介及socket,tcp,http三者之间的区别和原理
1.OSI模型简介(七层网络模型) OSI 模型(Open System Interconnection model):一个由国际标准化组织提出的概念模型,试图提供一个使各种不同的计算机和网络在世界范围内实现互联的标准框架。 它将计算机网络体系结构划分为七层,每…...

【leetcode】leetcode69 x的平方根
文章目录 给你一个非负整数 x ,计算并返回 x 的 算术平方根 。原理牛顿法(数值分析中使用到的):二分法 解决方案java 实现实例执行结果 python 实现实例 给你一个非负整数 x ,计算并返回 x 的 算术平方根 。 由于返回类型是整数&…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...

Python爬虫实战:研究Restkit库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的有价值数据。如何高效地采集这些数据并将其应用于实际业务中,成为了许多企业和开发者关注的焦点。网络爬虫技术作为一种自动化的数据采集工具,可以帮助我们从网页中提取所需的信息。而 RESTful API …...

深入解析光敏传感技术:嵌入式仿真平台如何重塑电子工程教学
一、光敏传感技术的物理本质与系统级实现挑战 光敏电阻作为经典的光电传感器件,其工作原理根植于半导体材料的光电导效应。当入射光子能量超过材料带隙宽度时,价带电子受激发跃迁至导带,形成电子-空穴对,导致材料电导率显著提升。…...

HTML版英语学习系统
HTML版英语学习系统 这是一个完全免费、无需安装、功能完整的英语学习工具,使用HTML CSS JavaScript实现。 功能 文本朗读练习 - 输入英文文章,系统朗读帮助练习听力和发音,适合跟读练习,模仿学习;实时词典查询 - 双…...
