【LeetCode 算法】Handling Sum Queries After Update 更新数组后处理求和查询-Segment Tree
Handling Sum Queries After Update 更新数组后处理求和查询
问题描述:
给你两个下标从 0 开始的数组 n u m s 1 和 n u m s 2 nums1 和 nums2 nums1和nums2 ,和一个二维数组 q u e r i e s queries queries 表示一些操作。总共有 3 种类型的操作:
操作类型 1 为 q u e r i e s [ i ] = [ 1 , l , r ] queries[i] = [1, l, r] queries[i]=[1,l,r] 。你需要将 n u m s 1 nums1 nums1 从下标 l 到下标 r 的所有 0 反转成 1 或将 1 反转成 0 。l 和 r 下标都从 0 开始。
操作类型 2 为 q u e r i e s [ i ] = [ 2 , p , 0 ] queries[i] = [2, p, 0] queries[i]=[2,p,0] 。对于 0 < = i < n 0 <= i < n 0<=i<n 中的所有下标,令 n u m s 2 [ i ] = n u m s 2 [ i ] + n u m s 1 [ i ] ∗ p nums2[i] = nums2[i] + nums1[i] * p nums2[i]=nums2[i]+nums1[i]∗p 。
操作类型 3 为 q u e r i e s [ i ] = [ 3 , 0 , 0 ] queries[i] = [3, 0, 0] queries[i]=[3,0,0] 。求 nums2 中所有元素的和。
请你返回一个数组,包含所有第三种操作类型的答案。
1 < = n u m s 1. l e n g t h , n u m s 2. l e n g t h < = 1 0 5 n u m s 1. l e n g t h = n u m s 2. l e n g t h 1 < = q u e r i e s . l e n g t h < = 1 0 5 q u e r i e s [ i ] . l e n g t h = 3 0 < = l < = r < = n u m s 1. l e n g t h − 1 0 < = p < = 1 0 6 0 < = n u m s 1 [ i ] < = 1 0 < = n u m s 2 [ i ] < = 1 0 9 1 <= nums1.length,nums2.length <= 10^5\\ nums1.length = nums2.length\\ 1 <= queries.length <= 10^5\\ queries[i].length = 3\\ 0 <= l <= r <= nums1.length - 1\\ 0 <= p <= 10^6\\ 0 <= nums1[i] <= 1\\ 0 <= nums2[i] <= 10^9 1<=nums1.length,nums2.length<=105nums1.length=nums2.length1<=queries.length<=105queries[i].length=30<=l<=r<=nums1.length−10<=p<=1060<=nums1[i]<=10<=nums2[i]<=109
分析
这个问题给的2个数组nums1,nums2,同时还有query指令。
问题本身比较绕, n u m s 1 nums1 nums1是01数组,而 n u m s 2 nums2 nums2可以看成是由 n u m s 1 nums1 nums1的一个函数映射。
而每次的 q u e r y query query指令为3的时候,需要计算出 n u m s 2 nums2 nums2 的元素和。
如果是纯粹计算数组的元素和,是配不上这个hard。
没错,问题的query指令还有1和2,它们会对nums1进行修改,从而影响到nums2的元素,进而会影响到结果。
最原始的方式就是暴力。
-
q u e r y = = 1 query==1 query==1的时候,会将 n u m s 1 nums1 nums1中的区间 [ l , r ] [l,r] [l,r]的 01 01 01进行反转,即0变1,1变0,而产生的影响就是 [ l , r ] [l,r] [l,r]内的出现的1,会导致处于该区间内的 n u m s 2 [ i ] nums2[i] nums2[i],增加 n u m s 1 [ i ] ∗ p nums1[i]*p nums1[i]∗p.
-
q u e r y = = 1 query==1 query==1的时候,对 n u m s 1 nums1 nums1修改的时间复杂度为 O ( k ) O(k) O(k),k为区间的范围,
-
q u e r y = = 2 query==2 query==2,对 n u m s 2 nums2 nums2的修改时间复杂度是 O ( N ) O(N) O(N)。
-
q u e r y = = 3 query==3 query==3,要计算 s u m ( n u m s 2 ) sum(nums2) sum(nums2),时间复杂度 O ( N ) O(N) O(N).
那么整体的时间复杂度就是 O ( N 2 ) O(N^2) O(N2),到此暴力的模拟思路就可以完成了,结果TLE。
其实nums2这个数组,是一个中间数组,虽然是统计nums2的和,实际上并不需要得到nums2 的详细元素。
在该问题中nums2的和在指令执行的过程中一定是单调递增的,而且在 q u e r y = 1 query=1 query=1之后,区间 [ l , r ] [l,r] [l,r]产生了 x 个 1 x个1 x个1,那么这 x 个 1 x个1 x个1会影响到对应 n u m s 2 nums2 nums2对应这个区间的 n u m s 2 [ i ] nums2[i] nums2[i],效果就是这个区间的nums2的和增加了x*p 。
如果一开始nums1有x个1,那么nums2初始和为 s u m 1 sum_1 sum1,当进行了 q u e r y = = 1 query==1 query==1 的操作,nums1的某个区间出现了 x 1 x_1 x1个1,此时nums2的元素和就是 s u m 1 + x 1 ∗ p sum_1+x_1*p sum1+x1∗p.
所以如果可以快速的统计 n u m s 1 nums1 nums1在每个 q u e r y = = 1 query==1 query==1的操作下,区间产生的1的数量,就可以快速的累加到nums2的元素和上,这样就可以在 O ( 1 ) O(1) O(1)的时间复杂度下得到 q u e r y = = 3 query==3 query==3时的结果。
而能够达到这个效果的,就是线段树。而且线段树在解决这类问题中,更新和查询的时间复杂度都是 O ( l o g N ) O(logN) O(logN),所以整体的时间复杂度就是 O ( N l o g N ) O(NlogN) O(NlogN)
代码
线段树
public long[] handleQuery(int[] nums1, int[] nums2, int[][] queries) {int n = nums1.length, m = 0, i = 0;cnt1 = new int[n * 4];flip = new boolean[n * 4];build(nums1, 1, 1, n);long sum = 0L;for (var x : nums2){sum += x;}for (var q : queries){if (q[0] == 3) ++m;}long[] ans = new long[m];for (var q : queries) {if (q[0] == 1){update(1, 1, n, q[1] + 1, q[2] + 1); } else if (q[0] == 2){sum += (long) q[1] * cnt1[1]; } else{ans[i++] = sum;} }return ans;}// segment treeprivate int[] cnt1;private boolean[] flip;// 维护区间 1 的个数private void maintain(int o) {cnt1[o] = cnt1[o * 2] + cnt1[o * 2 + 1];}// 执行区间反转private void do_(int o, int l, int r) {cnt1[o] = r - l + 1 - cnt1[o];flip[o] = !flip[o];}// 初始化线段树 o,l,r=1,1,nprivate void build(int[] a, int o, int l, int r) {if (l == r) {cnt1[o] = a[l - 1];return;}int m = (l + r) / 2;build(a, o * 2, l, m);build(a, o * 2 + 1, m + 1, r);maintain(o);}// 反转区间 [L,R] o,l,r=1,1,nprivate void update(int o, int l, int r, int L, int R) {if (L <= l && r <= R) {do_(o, l, r);return;}int m = (l + r) / 2;if (flip[o]) {do_(o * 2, l, m);do_(o * 2 + 1, m + 1, r);flip[o] = false;}if (m >= L){update(o * 2, l, m, L, R);} if (m < R){update(o * 2 + 1, m + 1, r, L, R); } maintain(o);}
时间复杂度 O ( N l o g N ) O(NlogN) O(NlogN)
空间复杂度 O ( N ) O(N) O(N)
代码来源于 灵神大佬,略有调整,线段树写的很简洁。
Tag
Array
Segment Tree
相关文章:

【LeetCode 算法】Handling Sum Queries After Update 更新数组后处理求和查询-Segment Tree
文章目录 Handling Sum Queries After Update 更新数组后处理求和查询问题描述:分析代码线段树 Tag Handling Sum Queries After Update 更新数组后处理求和查询 问题描述: 给你两个下标从 0 开始的数组 n u m s 1 和 n u m s 2 nums1 和 nums2 nums1…...

基于Linux操作系统中的MySQL数据库SQL语句(三十一)
MySQL数据库SQL语句 目录 一、SQL语句类型 1、DDL 2、DML 3、DCL 4、DQL 二、数据库操作 1、查看 2、创建 2.1、默认字符集 2.2、指定字符集 3、进入 4、删除 5、更改 6、练习 三、数据表操作 (一)数据类型 1、数值类型 1.1、TINYINT …...
)
【Matlab】基于BP神经网络的数据回归预测新数据(Excel可直接替换数据)
【Matlab】基于BP神经网络的数据回归预测新数据(Excel可直接替换数据) 1.模型原理2.数学公式3.文件结构4.Excel数据5.分块代码5.1 main.m5.2 NewData.m6.完整代码6.1 main.m6.2 NewData.m7.运行结果1.模型原理 基于BP神经网络的数据回归预测是一种常见的机器学习方法,用于处…...
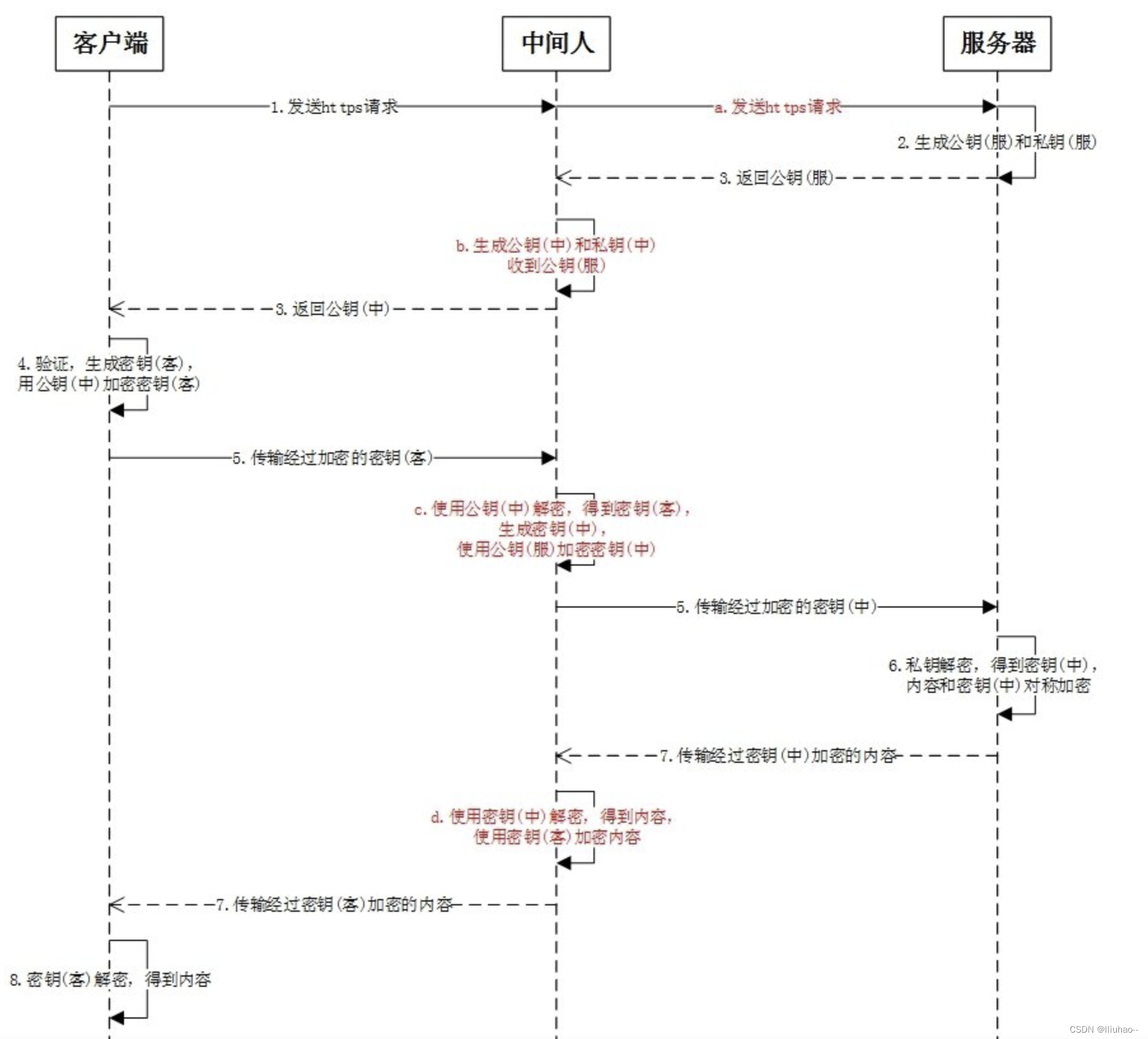
HTTPS连接过程中的中间人攻击
HTTPS连接过程中的中间人攻击 HTTPS连接过程中间人劫持攻击 HTTPS连接过程 https协议就是httpssl/tls协议,如下图所示为其连接过程: HTTPS连接的整个工程如下: https请求:客户端向服务端发送https请求;生成公钥和私…...
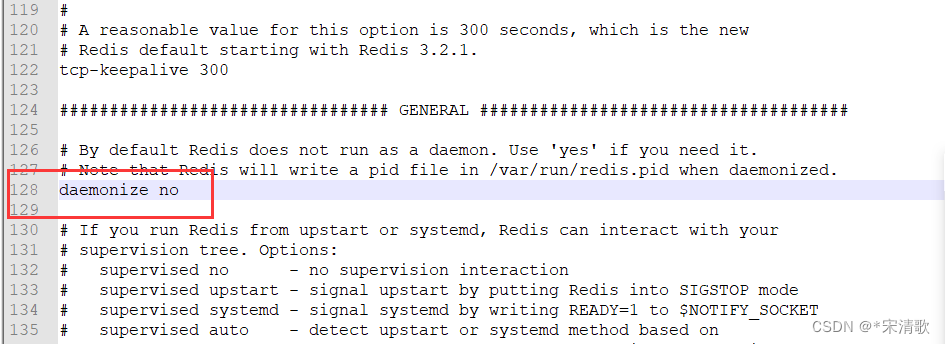
redis启动失败,oO0OoO0OoO0Oo Redis is starting oO0OoO0OoO0Oo
在redis文件夹下,启动redis正常。 但是加入到system后启动redis失败。 一直处于starting状态。 对比正常redis服务的配置之后,把redis.conf里的守护进程关掉就可以了(但是没用system管理之前,直接./redis.server启动是可以的&…...
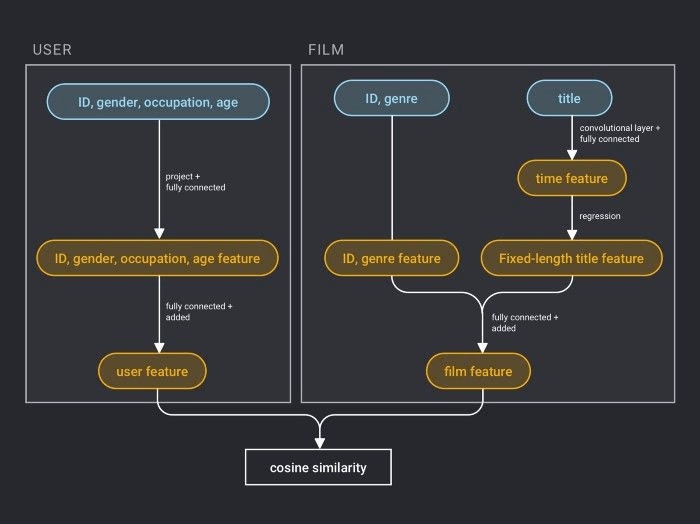
milvus: 专为向量查询与检索设计的向量数据库
1. 什么是milvus? milvus docs milvus release Milvus的目标是:store, index, and manage massive embedding vectors generated by deep neural networks and other machine learning (ML) models. Milvus 向量数据库专为向量查询与检索设计…...
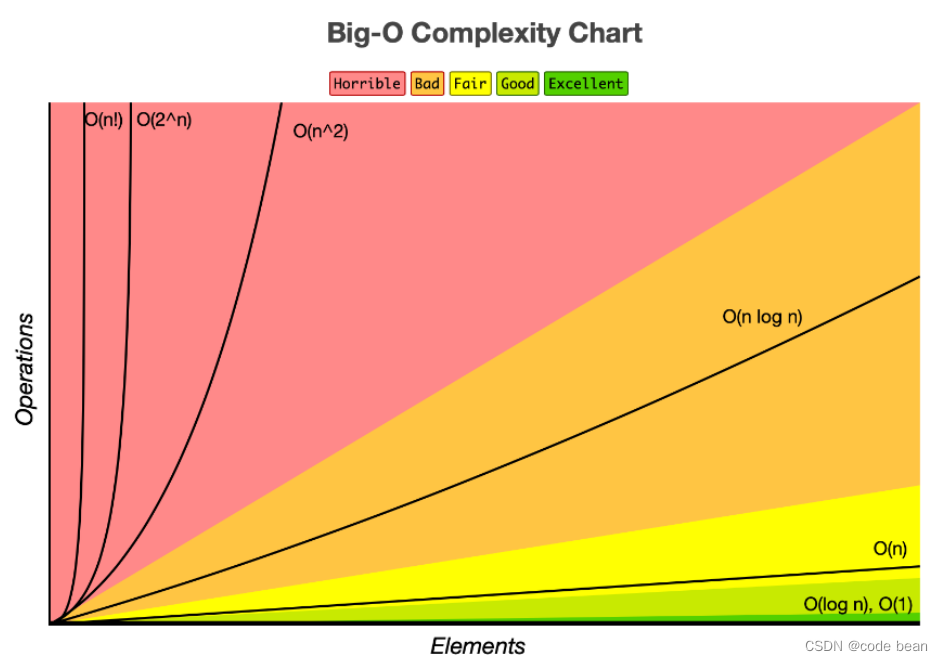
【C# 数据结构】Heap 堆
【C# 数据结构】Heap 堆 先看看C#中有那些常用的结构堆的介绍完全二叉树最大堆 Heap对类进行排序实现 IComparable<T> 接口 对CompareTo的一点解释 参考资料 先看看C#中有那些常用的结构 作为 数据结构系类文章 的开篇文章,我们先了解一下C# 有哪些常用的数据…...

智慧园区楼宇合集:数字孪生管控系统
智慧园区是指将物联网、大数据、人工智能等技术应用于传统建筑和基础设施,以实现对园区的全面监控、管理和服务的一种建筑形态。通过将园区内设备、设施和系统联网,实现数据的传输、共享和响应,提高园区的管理效率和运营效益,为居…...

Ajax 黑马学习
Ajax 资源 数据是服务器对外提供的资源,通过 请求 - 处理 - 响应方式获取 请求服务器数据, 用到 XMLHttpRequest 对象 XMLHttpRequest 是浏览器提供的js成员, 通过它可以请求服务器上的数据资源 let xmlHttpRequest new XMLHttpRequest(); 请求方式 : get向服务器获取数据…...

软件应用开发的常见环境
一般来说,在小型项目中可能只有开发环境和生产环境;在中型项目中会有开发环境、staging environment、生产环境;在大型项目中会有开发环境、测试环境、staging environment、生产环境。 一、Dev Env / Development Environment 开发环境 开…...
, into_iter(), iter_mut())
Rust中的iter(), into_iter(), iter_mut()
在Rust中,iter(), into_iter(), iter_mut()都是用于在集合类型上创建迭代器的方法。这三个方法各有不同,下面一一进行介绍。 iter(): iter() 方法创建一个不可变的引用迭代器。当你只想读取集合中的元素,而不想改变它们或消耗集合时ÿ…...

[SQL挖掘机] - 日期函数 - current_date
current_date函数时,它通常被用来获取当前的日期。它返回一个表示当前日期的日期值。 current_date函数没有任何参数,因此只需简单地调用它即可获得系统当前日期。 以下是一个示例: select current_date;这将返回当前日期,例如…...

JAVA面试总结-Redis篇章(三)——缓存雪崩
JAVA面试总结-Redis篇章(三)——缓存雪崩...
maven编译报错
参考链接:mvn打包No compiler is provided in this environment. Perhaps you are running on a JRE rather than a JDK_51CTO博客_mvn打包命令 在执行 yum install -y java-1.8.0-opensdk命令后,使用maven去编译打包,结果报错, …...

HPC集群调度系统和计算系统
什么是计算云? 所谓的计算云指的是为计算业务优化的类云基础架构,它强调用云的方式解决计算问题,而不是将“计算”搬到现有的公有云或者容器云上。 目前公有云或者容器云(例如k8s)上的HPC解决方案本质上都是将现有的H…...

pg_archivecleanup清理wal日志
一、 注意事项 pg_archivecleanup代码中仅进行了wal日志文件名的对比,没有实现对WAL日志名及对应生成时间的判断。在WAL日志未被重命名时,时间与日志名顺序名一致,没有问题。一旦WAL日志被重命名,pg_archivecleanup清理就可能清理…...
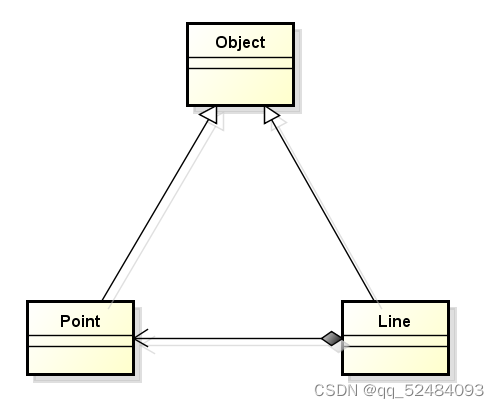
继承中的访问级别
值得思考的问题 子类是否可以直接访问父类的私有成员? 思考过程 继承中的访问级别 面向对象中的访问级别不止是 public 和 private 可以定义 protected 访问级别 关键字 protected 的意义 修饰的成员不能被外界直接访问修饰的成员可以被子类直接访问 思考 为什…...
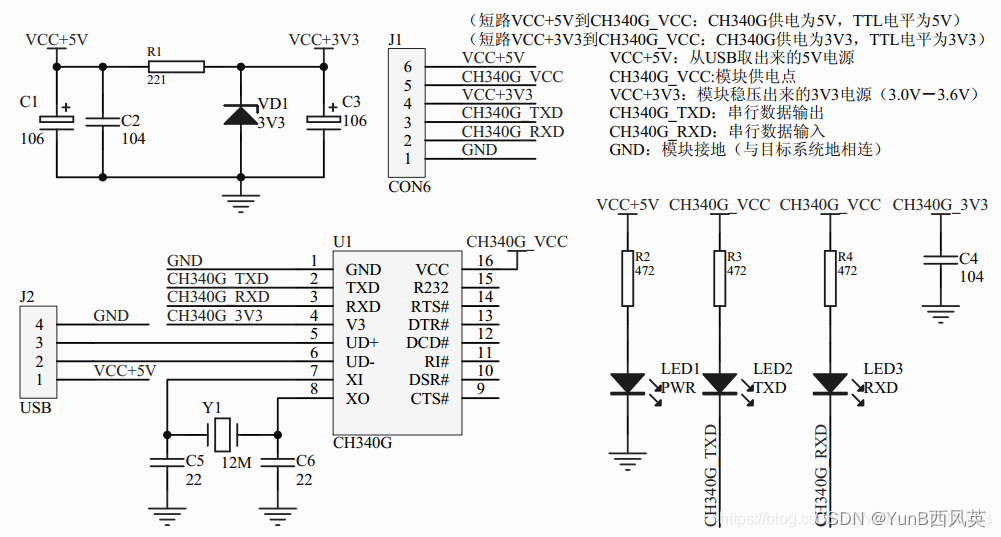
(学习日记)2023.06.09
写在前面: 由于时间的不足与学习的碎片化,写博客变得有些奢侈。 但是对于记录学习(忘了以后能快速复习)的渴望一天天变得强烈。 既然如此 不如以天为单位,以时间为顺序,仅仅将博客当做一个知识学习的目录&a…...

激光雷达-相机联合标定
https://f.daixianiu.cn/csdn/9499401684344864.html ros usb相机内参标定 ROS系统-摄像头标定camera calibration_berry丶的博客-CSDN博客...
[golang gin框架] 40.Gin商城项目-微服务实战之Captcha验证码微服务
本次内容需要 gin框架基础知识, golang微服务基础知识才能更好理解 一.Captcha验证码功能引入 在前面,讲解了微服务的架构等,这里,来讲解前面商城项目的 Captcha验证码 微服务 ,captcha验证码功能在前台,后端 都要用到 ,可以把它 抽离出来 ,做成微服务功能 编辑 这个验证码功能…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
