【R3F】0.9添加 shadow
开启使用shadow
-
在
canvas设置属性shadows -
在对应的 mesh 中设置 产生阴影
castShadow和接收阴影receiveShadow设置完成之后,即可实现阴影...<Canvas shadows > <mesh castShadow ><boxGeometry /><meshStandardMaterial color="mediumpurple" /> </mesh> <mesh receiveShadow position-y={-1} scale={20} rotation-x={-Math.PI * .5}><planeGeometry /><meshStandardMaterial color="greenyellow" /> </mesh> </Canvas> ...
设置灯光阴影
-
可以有两种方式,第一种方式直接设置属性,第二种方式是根据节点设置
// 方式 1 <directionalLight ref={directionalLight}position={[1, 2, 3]}intensity={1.5}castShadowshadow-mapSize
相关文章:

【R3F】0.9添加 shadow
开启使用shadow 在 canvas 设置属性shadows 在对应的 mesh 中设置 产生阴影castShadow和接收阴影receiveShadow 设置完成之后,即可实现阴影 ...<Canvas shadows > <mesh castShadow ><boxGeometry /><meshStandardMaterial color="mediumpurple&qu…...
【JavaEE初阶】HTTP请求的构造及HTTPS
文章目录 1.HTTP请求的构造1.1 from表单请求构造1.2 ajax构造HTTP请求1.3 Postman的使用 2. HTTPS2.1 什么是HTTPS?2.2 HTTPS中的加密机制(SSL/TLS)2.2.1 HTTP的安全问题2.2.2 对称加密2.2.3 非对称加密2.2.3 中间人问题2.2.5 证书 1.HTTP请求的构造 常见的构造HTTP 请求的方…...

探索和实践:基于Python的TD-PSOLA语音处理算法应用与优化
今天我将和大家分享一个非常有趣且具有挑战性的主题:TD-PSOLA语音处理算法在Python中的应用。作为一种在语音合成和变换中广泛使用的技术,TD-PSOLA (Time-Domain Pitch-Synchronous Overlap-Add) 提供了一种改变语音音高和时间长度而不产生显著失真的有效方法。在本篇博客中,…...
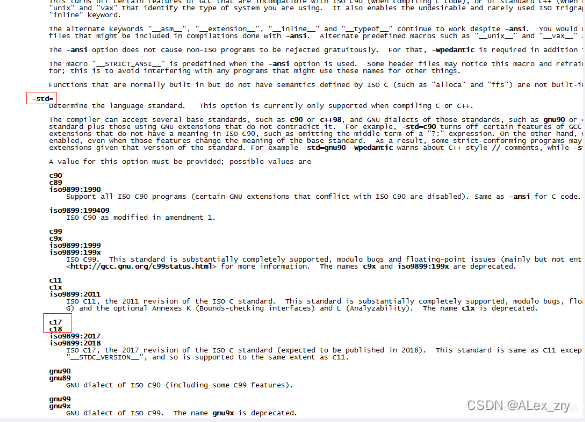
Linux 下centos 查看 -std 是否支持 C17
实际工作中,可能会遇到c的一些高级特性,例如std::invoke,此函数是c17才引入的,如何判断当前的gcc是否支持c17呢,这里提供两种办法。 1.根据gcc的版本号来推断 gcc --version,可以查看版本号,笔者…...

【算法训练营】字符串转成整数
字符串转成整数 题目题解代码 题目 点击跳转: 把字符串转换为整数 题解 【题目解析】: 本题本质是模拟实现实现C库函数atoi,不过参数给的string对象 【解题思路】: 解题思路非常简单,就是上次计算的结果10,相当于10…...

入局元宇宙,所谓的无限可能到底在哪里?
最近的热点新闻表明,人们似乎认为元宇宙已经走向“死亡”。但实际上,市场应该重新定义对元宇宙的看法,以及正视它最大的机会所在——游戏领域。 1937年5月6日,一架名为兴登堡号的巨大氢能齐柏林飞艇飞临新泽西州曼彻斯特镇上空&a…...
的端口号是 22 !!)
为什么 SSH(安全终端)的端口号是 22 !!
导读为什么 SSH(安全终端)的端口号是 22 呢,这不是一个巧合,这其中有个我(Tatu Ylonen,SSH 协议的设计者)未曾诉说的故事。 将 SSH 协议端口号设为 22 的故事 1995 年春我编写了 SSH 协议的最…...

k8s Label 2
在 k8s 中,我们会轻轻松松的部署几十上百个微服务,这些微服务的版本,副本数的不同进而会带出更多的 pod 这么多的 pod ,如何才能高效的将他们组织起来的,如果组织不好便会让管理微服务变得混乱不堪,杂乱无…...

layui踩坑记录之form表单下的button按钮默认自动提交
首先参考下面这篇文章: layui form表单下的button按钮会自动提交表单的问题以及解决方案_layui form里面其他button按钮_你用点心就行的博客-CSDN博客 他说的已经很清楚了,我再补充(啰嗦)一下: 其实就是使用form的时…...
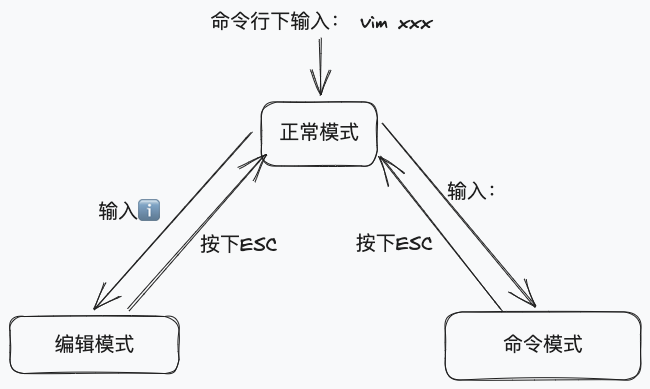
2-vi和vim的使用
vi和vim的区别 vi 是linux系统中内置的文本编辑器vim具有程序编辑能力 vi和vim常用的三种模式 正常模式 使用vim打开一个文件,就默认进入正常模式可以使用方向键【上下左右】来移动光标可以使用【删除字符/删除整行】来处理文件内容也可以使用【复制/粘贴】快捷键…...

微服务——Nacos配置管理
目录 Nacos配置管理——实现配置管理 配置管理实践 Nacos配置管理——微服务配置拉取 Nacos配置管理——配置热更新 方式一: 编辑 方式二(推荐方式): Nacos配置管理——多环境配置共享 优先级问题 Nacos配置管理——nacos集群搭建 总结编辑 Nacos配置管理——实现配置管…...
如何为WordPress博客网站配置免费域名HTTPS证书
文章目录 如何为WordPress博客网站配置免费域名HTTPS证书前置条件:步骤1 申请免费的域名HTTPS证书步骤2 将HTTP证书配置到cpolar的配置文件中2.1 创建证书文件夹2.2 修改cpolar配置文件2.3 重启cpolar服务2.4 查看后台Wordpress隧道是否在线正常2.5 用浏览器打开站点…...

React之内置的高阶组件
React之内置的高阶组件 React内置了一些高阶组件,以便对一些组件做特殊处理,从而提高代码性能。例如React.memo、React.forwardRef 注意:高阶组件不是Reacts视图组件 什么是高阶组件 高阶组件本质是高阶函数。高阶组件接收一个组件作为参数&…...
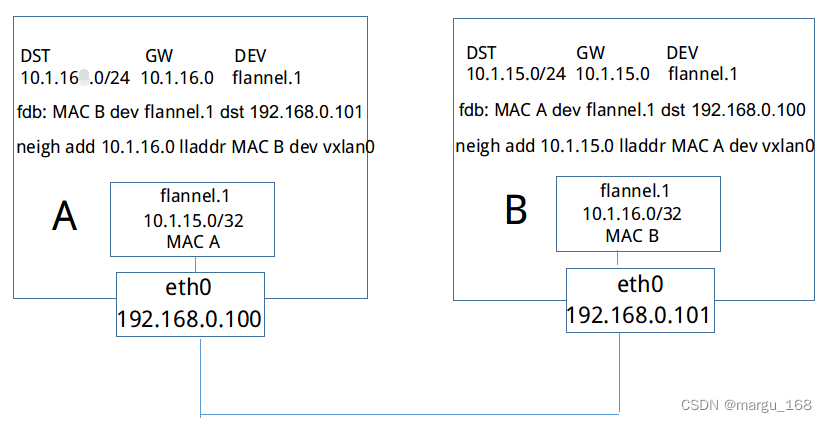
【kubernetes系列】flannel之vxlan模式原理
概述 在Kubernetes中要保证容器之间网络互通,网络至关重要。而Kubernetes本身并没有自己实现容器网络,而是而是借助CNI标准,通过插件化的方式自由接入进来。在容器网络接入进来需要满足如下基本原则: Pod无论运行在任何节点都可…...

PostgreSQL -- 备份恢复命令
前言 这是我在这个网站整理的笔记,关注我,接下来还会持续更新。 作者:RodmaChen PostgreSQL -- 备份恢复命令 一. pg_dump常用参数二. pg_dumpall三. psql四. pg_restore五.参考文章 PostgreSQL 13.7 一. pg_dump常用参数 pg_dump 把一个数据…...
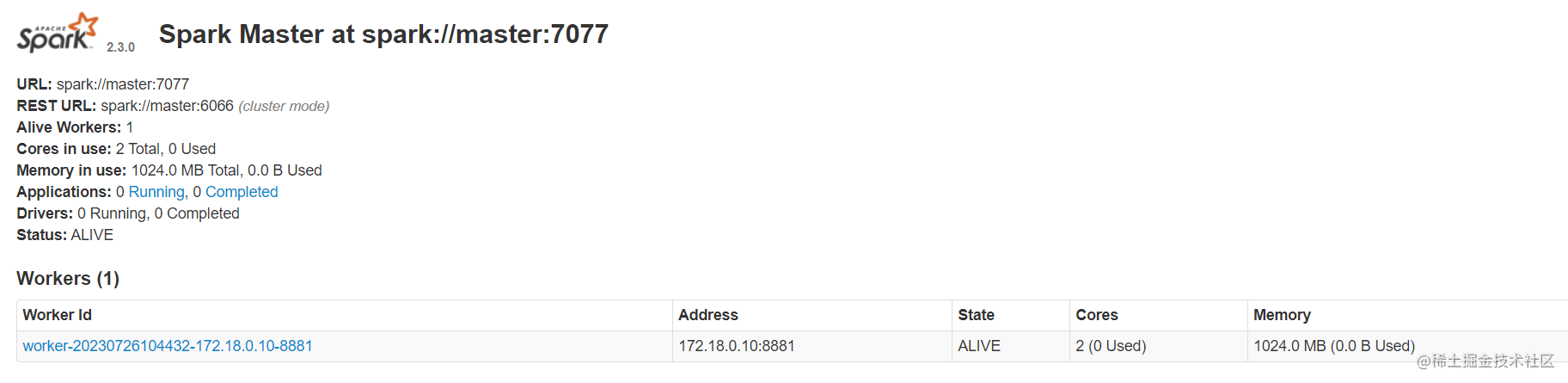
【基于Spark的电影推荐系统】环境准备
概览 本科毕设做过电影推荐系统,但当时的推荐算法只有一个,现在已经忘记大部分了,当时也没有记录,因此写这个博客重新来记录一下。此外,技术栈由于快秋招原因来不及做过多的部分,因此只实现简单的功能&…...

团簇大小分布计算方法,fix ave/histo命令详解
LAMMPS是一款广泛应用于分子动力学模拟的强大软件。在模拟过程中,我们经常需要对系统的物理性质进行分析和统计。 fix ave/histo命令则是LAMMPS中一个非常有用的命令,它可以帮助我们对系统进行直方图统计分析。 本文将深入介绍fix ave/histo命令的用法和…...

CAN标准帧和拓展帧
转自:https://www.cnblogs.com/fengliu-/p/9277165.html CAN2.0B标准帧 CAN 标准帧信息为11个字节,包括两部分:信息和数据部分。前3个字节为信息部分。 位置 7 6 5 4 3 2 1 0 字节01 FF RTR DLC(数据长度&#…...

android 清除缓存方法
获得应用的存储信息 private void getAppStorageInfo(String packageName){StorageStatsManager storageStatsManager (StorageStatsManager) context.getSystemService(Context.STORAGE_STATS_SERVICE);StorageManager storageManager (StorageManager) context.getSystemS…...

介绍下你们项目中各微服务之间怎么调用的?
各微服务模块之间的数据交互主要通过一些常见的通信机制进行。以下是几种常见的数据交互方式: RESTful API:REST(Representational State Transfer)是一种基于HTTP协议的通信机制,它使用标准的HTTP方法(如…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...
