实验06 二叉树遍历及应用2022
A. 【程序填空】二叉树三种遍历
题目描述
给定一颗二叉树的特定先序遍历结果,空树用字符‘0’表示,例如AB0C00D00表示如下图
请完成以下程序填空,建立该二叉树的二叉链式存储结构,并输出该二叉树的先序遍历、中序遍历和后序遍历结果
输入
第一行输入一个整数t,表示有t个二叉树
第二行起输入每个二叉树的特定先序遍历结果,空树用字符‘0’表示,连续输入t行
输出
每个二叉树输出三行,对应先序遍历、中序遍历和后序遍历结果
输入:
2
AB0C00D00
AB00C00
输出:
ABCD
BCAD
CBDA
ABC
BAC
BCA代码:
#include <iostream>
#include <string>
using namespace std;
class BiTreeNode {
public:char data; //数据域BiTreeNode* leftChild, * rightChild; //左右子树指针BiTreeNode() :leftChild(NULL), rightChild(NULL) {}~BiTreeNode() {}
};class BiTree {
private:BiTreeNode* root; //根结点指针string sTree; //建树字符串int pos; //标识建树字符串的当前字符位置BiTreeNode* CreateTree();//建树私有函数void PreOrder(BiTreeNode* t); //先序遍历实现void InOrder(BiTreeNode* t); //中序遍历实现void PostOrder(BiTreeNode* t); //后序遍历实现
public:BiTree() :root(NULL) {};void Create(string vArray); //建树公有接口,参数是特定的先序遍历字符串void PreOrder(); //先序遍历公有接口void InOrder(); //中序遍历公有接口void PostOrder(); //后序遍历公有接口
};
//二叉树公有接口的实现
void BiTree::Create(string vArray)
{pos = 0;sTree.assign(vArray); //把参数保存到内部字符串root = CreateTree(); //建树成功后root指向根结点
}
void BiTree::PreOrder()
{PreOrder(root);
}
void BiTree::InOrder()
{InOrder(root);
}
void BiTree::PostOrder()
{PostOrder(root);
}//请完成上述类内部的私有函数实现
/********** Write your code here! **********/
BiTreeNode* BiTree::CreateTree() {BiTreeNode* T=new BiTreeNode;char c = sTree[pos++];if (c == '0') T = NULL;else {T->data = c;T->leftChild=CreateTree();T->rightChild =CreateTree();}return T;
}void BiTree::PreOrder(BiTreeNode* t) {if (t == NULL) return;else {cout << t->data;PreOrder(t->leftChild);PreOrder(t->rightChild);}
}
void BiTree::InOrder(BiTreeNode* t) {if (t == NULL) return;else {InOrder(t->leftChild);cout << t->data;InOrder(t->rightChild);}
}void BiTree::PostOrder(BiTreeNode* t) {if (t == NULL) return;else {PostOrder(t->leftChild);PostOrder(t->rightChild);cout << t->data;}
}
/*******************************************/
//主函数
int main()
{int t;string vArray;cin >> t;while (t--){cin >> vArray;BiTree myTree;myTree.Create(vArray);myTree.PreOrder(); cout << endl;myTree.InOrder(); cout << endl;myTree.PostOrder(); cout << endl;}return 0;
}
B. DS二叉树--叶子数量
题目描述
计算一颗二叉树包含的叶子结点数量。
提示:叶子是指它的左右孩子为空。
建树方法采用“先序遍历+空树用0表示”的方法,即给定一颗二叉树的先序遍历的结果为AB0C00D00,其中空节点用字符‘0’表示。则该树的逻辑结构如下图。
输入
第一行输入一个整数t,表示有t个测试数据
第二行起输入二叉树先序遍历的结果,空树用字符‘0’表示,输入t行
输出
逐行输出每个二叉树的包含的叶子数量
输入:
3
AB0C00D00
AB00C00
ABC00D00E00输出:
2
2
3代码:
#include <iostream>
#include <string>
using namespace std;
class BiTreeNode {
public:char data; //数据域BiTreeNode* leftChild, * rightChild; //左右子树指针BiTreeNode() :leftChild(NULL), rightChild(NULL) {}~BiTreeNode() {}
};class BiTree {
private:BiTreeNode* root; //根结点指针string sTree; //建树字符串int pos; //标识建树字符串的当前字符位置BiTreeNode* CreateTree();//建树私有函数void PreOrder(BiTreeNode* t); //先序遍历实现void InOrder(BiTreeNode* t); //中序遍历实现void PostOrder(BiTreeNode* t); //后序遍历实现int Leafnum(BiTreeNode* t);
public:BiTree() :root(NULL) {};void Create(string vArray); //建树公有接口,参数是特定的先序遍历字符串void PreOrder(); //先序遍历公有接口void InOrder(); //中序遍历公有接口void PostOrder(); //后序遍历公有接口int Leafnum();
};
//二叉树公有接口的实现
void BiTree::Create(string vArray)
{pos = 0;sTree.assign(vArray); //把参数保存到内部字符串root = CreateTree(); //建树成功后root指向根结点
}
void BiTree::PreOrder()
{PreOrder(root);
}
void BiTree::InOrder()
{InOrder(root);
}
void BiTree::PostOrder()
{PostOrder(root);
}int BiTree::Leafnum() {return Leafnum(root);
}
//请完成上述类内部的私有函数实现
/********** Write your code here! **********/
BiTreeNode* BiTree::CreateTree() {BiTreeNode* T = new BiTreeNode;char c = sTree[pos++];if (c == '0') T = NULL;else {T->data = c;T->leftChild = CreateTree();T->rightChild = CreateTree();}return T;
}void BiTree::PreOrder(BiTreeNode* t) {if (t == NULL) return;else {cout << t->data;PreOrder(t->leftChild);PreOrder(t->rightChild);}
}
void BiTree::InOrder(BiTreeNode* t) {if (t == NULL) return;else {InOrder(t->leftChild);cout << t->data;InOrder(t->rightChild);}
}void BiTree::PostOrder(BiTreeNode* t) {if (t == NULL) return;else {PostOrder(t->leftChild);PostOrder(t->rightChild);cout << t->data;}
}
int BiTree::Leafnum(BiTreeNode* t) {if (t == NULL) return 0;else if ((t->leftChild == NULL) && (t->rightChild == NULL)) return 1;else return Leafnum(t->leftChild) + Leafnum(t->rightChild);}
/*******************************************/
//主函数
int main()
{int t;string vArray;cin >> t;while (t--){cin >> vArray;BiTree myTree;myTree.Create(vArray);cout << myTree.Leafnum()<<endl;}return 0;
}C. DS二叉树——二叉树之父子结点
题目描述
给定一颗二叉树的逻辑结构如下图,(先序遍历的结果,空树用字符‘0’表示,例如AB0C00D00),建立该二叉树的二叉链式存储结构。
编写程序输出该树的所有叶子结点和它们的父亲结点
输入
第一行输入一个整数t,表示有t个二叉树
第二行起,按照题目表示的输入方法,输入每个二叉树的先序遍历,连续输入t行
输出
第一行按先序遍历,输出第1个示例的叶子节点
第二行输出第1个示例中与叶子相对应的父亲节点
以此类推输出其它示例的结果
输入:
3
AB0C00D00
AB00C00
ABCD0000EF000输出:
C D
B A
B C
A A
D F
C E 代码:
#include <iostream>
#include <string>
#include<queue>
using namespace std;
class BiTreeNode {
public:char data; //数据域BiTreeNode* leftChild, * rightChild; //左右子树指针BiTreeNode() :leftChild(NULL), rightChild(NULL) {}~BiTreeNode() {}
};class BiTree {
private:BiTreeNode* root; //根结点指针string sTree; //建树字符串int pos; //标识建树字符串的当前字符位置BiTreeNode* CreateTree();//建树私有函数void PreOrder(BiTreeNode* t); //先序遍历实现void InOrder(BiTreeNode* t); //中序遍历实现void PostOrder(BiTreeNode* t); //后序遍历实现int Leafnum(BiTreeNode* t);int depth(BiTreeNode* t);void leaf(BiTreeNode* t);void levelOrder(BiTreeNode* t);
public:BiTree() :root(NULL) {};void Create(string vArray); //建树公有接口,参数是特定的先序遍历字符串void PreOrder(); //先序遍历公有接口void InOrder(); //中序遍历公有接口void PostOrder(); //后序遍历公有接口int Leafnum();int depth();void leaf();void levelOrder();
};
queue<BiTreeNode*> bt;
bool isleaf(BiTreeNode* t) {if ((t->leftChild == NULL) && (t->rightChild == NULL)) return true;else return false;
}
//二叉树公有接口的实现
void BiTree::Create(string vArray)
{pos = 0;sTree.assign(vArray); //把参数保存到内部字符串root = CreateTree(); //建树成功后root指向根结点
}
void BiTree::PreOrder()
{PreOrder(root);
}
void BiTree::InOrder()
{InOrder(root);
}
void BiTree::PostOrder()
{PostOrder(root);
}
int BiTree::Leafnum() {return Leafnum(root);
}
int BiTree::depth() {return depth(root);
}
void BiTree::leaf() {leaf(root);
}
void BiTree::levelOrder() {levelOrder(root);
}
//请完成上述类内部的私有函数实现
/********** Write your code here! **********/
BiTreeNode* BiTree::CreateTree() {BiTreeNode* T = new BiTreeNode;char c = sTree[pos++];if (c == '0') T = NULL;else {T->data = c;T->leftChild = CreateTree();T->rightChild = CreateTree();}return T;
}void BiTree::PreOrder(BiTreeNode* t) {if (t == NULL) return;else {cout << t->data;PreOrder(t->leftChild);PreOrder(t->rightChild);}
}
void BiTree::InOrder(BiTreeNode* t) {if (t == NULL) return;else {InOrder(t->leftChild);cout << t->data;InOrder(t->rightChild);}
}void BiTree::PostOrder(BiTreeNode* t) {if (t == NULL) return;else {PostOrder(t->leftChild);PostOrder(t->rightChild);cout << t->data;}
}int BiTree::Leafnum(BiTreeNode* t) {if (t == NULL) return 0;else if ((t->leftChild == NULL) && (t->rightChild == NULL)) return 1;else return Leafnum(t->leftChild) + Leafnum(t->rightChild);
}int BiTree::depth(BiTreeNode* t) {if (t == NULL) return 0;else return depth(t->leftChild) > depth(t->rightChild) ? depth(t->leftChild) + 1 : depth(t->rightChild) + 1;
}void BiTree::leaf(BiTreeNode* t) {if (t == NULL) return;else if (isleaf(t)) {bt.push(t);cout << t->data << " ";}else {leaf(t->leftChild);leaf(t->rightChild);}
}void BiTree::levelOrder(BiTreeNode* t) {queue<BiTreeNode*>tq;BiTreeNode* p = t;if (p) tq.push(p);while (!tq.empty()) {cout << tq.front()->data ;if (tq.front()->leftChild) tq.push(tq.front()->leftChild);if (tq.front()->rightChild) tq.push(tq.front()->rightChild);tq.pop();}
}/*******************************************/
//主函数
int main()
{int t;string vArray;cin >> t;while (t--){cin >> vArray;BiTree myTree;myTree.Create(vArray);myTree.levelOrder();cout << endl;}return 0;
}D. DS二叉树--层次遍历
题目描述
层次遍历二叉树,是从根结点开始遍历,按层次次序“自上而下,从左至右”访问树中的各结点。
建树方法采用“先序遍历+空树用0表示”的方法
要求:采用队列对象实现,函数框架如下:
输入
第一行输入一个整数t,表示有t个测试数据
第二行起输入二叉树先序遍历的结果,空树用字符‘0’表示,输入t行
输出
逐行输出每个二叉树的层次遍历结果
输入:
2
AB0C00D00
ABCD00E000FG00H0I00输出:
ABDC
ABFCGHDEI代码:
#include <iostream>
#include <string>
using namespace std;
class BiTreeNode {
public:char data; //数据域BiTreeNode* leftChild, * rightChild; //左右子树指针BiTreeNode() :leftChild(NULL), rightChild(NULL) {}~BiTreeNode() {}
};class BiTree {
private:BiTreeNode* root; //根结点指针string sTree; //建树字符串int pos; //标识建树字符串的当前字符位置BiTreeNode* CreateTree();//建树私有函数void PreOrder(BiTreeNode* t); //先序遍历实现void InOrder(BiTreeNode* t); //中序遍历实现void PostOrder(BiTreeNode* t); //后序遍历实现int Leafnum(BiTreeNode* t);int depth(BiTreeNode* t);
public:BiTree() :root(NULL) {};void Create(string vArray); //建树公有接口,参数是特定的先序遍历字符串void PreOrder(); //先序遍历公有接口void InOrder(); //中序遍历公有接口void PostOrder(); //后序遍历公有接口int Leafnum();int depth();
};
//二叉树公有接口的实现
void BiTree::Create(string vArray)
{pos = 0;sTree.assign(vArray); //把参数保存到内部字符串root = CreateTree(); //建树成功后root指向根结点
}
void BiTree::PreOrder()
{PreOrder(root);
}
void BiTree::InOrder()
{InOrder(root);
}
void BiTree::PostOrder()
{PostOrder(root);
}int BiTree::Leafnum() {return Leafnum(root);
}
int BiTree::depth() {return depth(root);
}
//请完成上述类内部的私有函数实现
/********** Write your code here! **********/
BiTreeNode* BiTree::CreateTree() {BiTreeNode* T = new BiTreeNode;char c = sTree[pos++];if (c == '0') T = NULL;else {T->data = c;T->leftChild = CreateTree();T->rightChild = CreateTree();}return T;
}void BiTree::PreOrder(BiTreeNode* t) {if (t == NULL) return;else {cout << t->data;PreOrder(t->leftChild);PreOrder(t->rightChild);}
}
void BiTree::InOrder(BiTreeNode* t) {if (t == NULL) return;else {InOrder(t->leftChild);cout << t->data;InOrder(t->rightChild);}
}void BiTree::PostOrder(BiTreeNode* t) {if (t == NULL) return;else {PostOrder(t->leftChild);PostOrder(t->rightChild);cout << t->data;}
}
int BiTree::Leafnum(BiTreeNode* t) {if (t == NULL) return 0;else if ((t->leftChild == NULL) && (t->rightChild == NULL)) return 1;else return Leafnum(t->leftChild) + Leafnum(t->rightChild);
}
int BiTree::depth(BiTreeNode* t) {if (t == NULL) return 0;else return depth(t->leftChild) > depth(t->rightChild) ? depth(t->leftChild) + 1 : depth(t->rightChild) + 1;
}
/*******************************************/
//主函数
int main()
{int t;string vArray;cin >> t;while (t--){cin >> vArray;BiTree myTree;myTree.Create(vArray);cout << myTree.depth() << endl;}return 0;
}相关文章:

实验06 二叉树遍历及应用2022
A. 【程序填空】二叉树三种遍历题目描述给定一颗二叉树的特定先序遍历结果,空树用字符‘0’表示,例如AB0C00D00表示如下图请完成以下程序填空,建立该二叉树的二叉链式存储结构,并输出该二叉树的先序遍历、中序遍历和后序遍历结果输…...

基于蜣螂算法改进的LSTM分类算法-附代码
基于蜣螂算法改进的LSTM分类算法 文章目录基于蜣螂算法改进的LSTM分类算法1.数据集2.LSTM模型3.基于蜣螂算法优化的RF4.测试结果5.Matlab代码摘要:为了提高LSTM数据的分类预测准确率,对LSTM中的参数利用蜣螂搜索算法进行优化。1.数据集 数据的来源是 UC…...

如何正确应用GNU GPLv3 和 LGPLv3 协议
文章目录前言GNU GPLv3.0Permissions(许可)Conditions(条件)Limitations(限制)GNU LGPLv3.0应用GPLv3.0应用LGPLv3.0建议的内容:添加文件头声明附录GNU GPLv3.0原文GNU LGPLv3.0 原文前言 对于了解开源的朋友们,GNU GPL系列协议可谓是老朋友了。原来我基…...
)
Python局部函数及用法(包含nonlocal关键字)
Python 函数内部可以定义变量,这样就产生了局部变量,可能有人会问,Python 函数内部能定义函数吗?答案是肯定的。Python 支持在函数内部定义函数,此类函数又称为局部函数。 那么,局部函数有哪些特征&#x…...

关于BMS的介绍及应用领域
电池管理系统(Battery Management System,BMS)是一种集成电路系统,它用于监测和控制电池系统状态,以确保电池的正常运行和安全使用。BMS的应用涵盖了电动汽车、储能系统、无人机、电动工具等各个领域,可以提…...

2月datawhale组队学习:大数据
文章目录一、大数据概述二、 Hadoop2.1 Hadoop概述2.2 su:Authentication failure2.3 使用sudo命令报错xxx is not in the sudoers file. This incident will be reported.2.4 创建用户datawhale,安装java8:2.5 安装单机版Hadoop2.5.1 安装Hadoop2.5.2 修…...

在Spring框架中创建Bean实例的几种方法
我们希望Spring框架帮忙管理Bean实例,以便得到框架所带来的种种功能,例如依赖注入等。将一个类纳入Spring容器管理的方式有几种,它们可以解决在不同场景下创建实例的需求。 XML配置文件声明 <?xml version"1.0" encoding"…...
PyQt5 界面预览工具
简介 一款为了预览PyQt5设计的UI界面而开发的工具,使用时需要结合PyCharm同时使用。 下载 PyQt5界面预览工具 参数说明 使用配置 启动PyCharm,找到File -> Settings,打开 找到Tools -> External Tools点击打开,在新界面…...

day44【代码随想录】动态规划之零钱兑换II、组合总和 Ⅳ、零钱兑换
文章目录前言一、零钱兑换II(力扣518)二、组合总和 Ⅳ(力扣377)三、零钱兑换(力扣322)总结前言 1、零钱兑换II 2、组合总和 Ⅳ 3、零钱兑换 一、零钱兑换II(力扣518) 给你一个整数…...
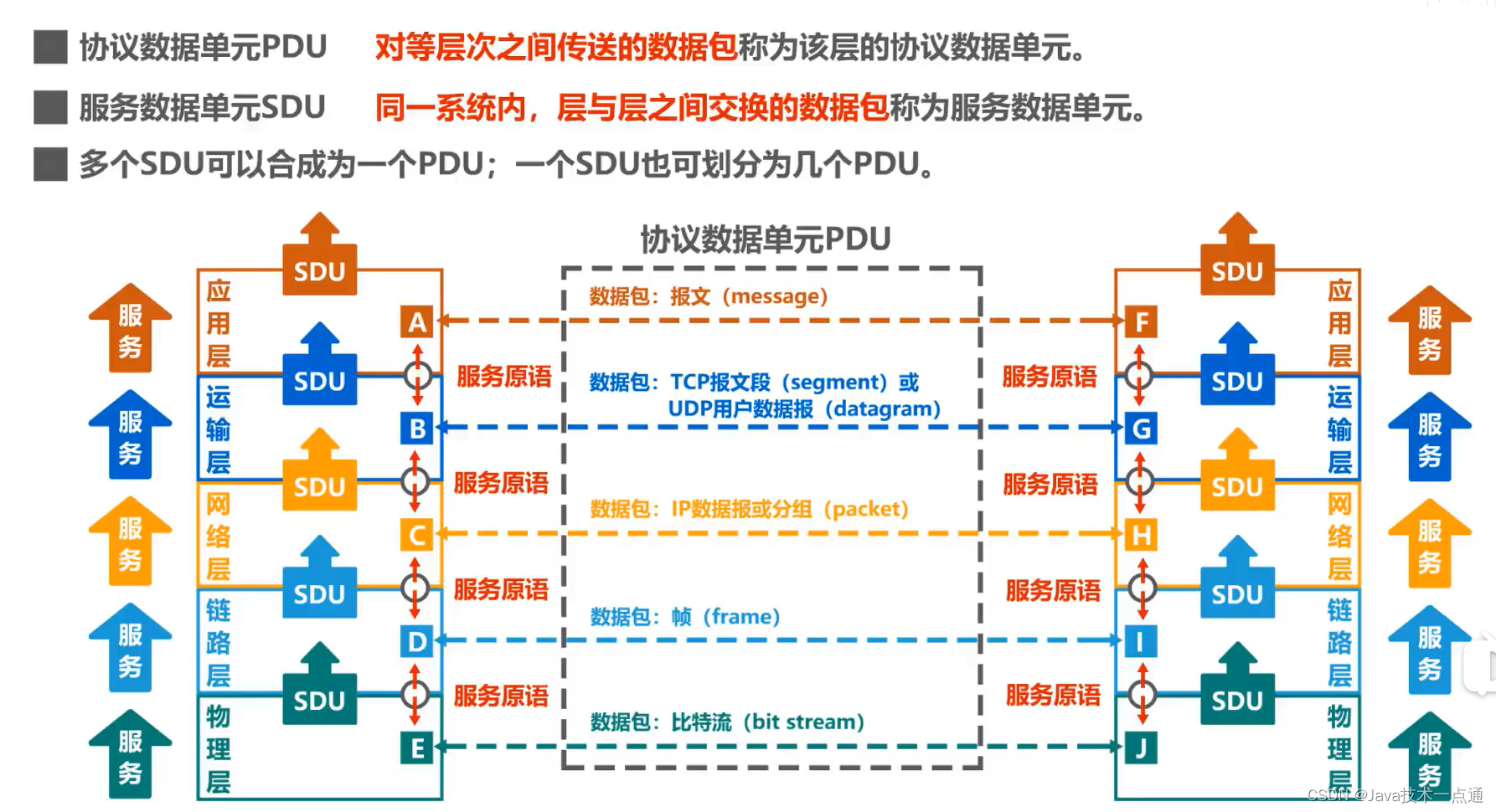
计算机网络第1章(概述)学习笔记
❤ 作者主页:欢迎来到我的技术博客😎 ❀ 个人介绍:大家好,本人热衷于Java后端开发,欢迎来交流学习哦!( ̄▽ ̄)~* 🍊 如果文章对您有帮助,记得关注、点赞、收藏、…...
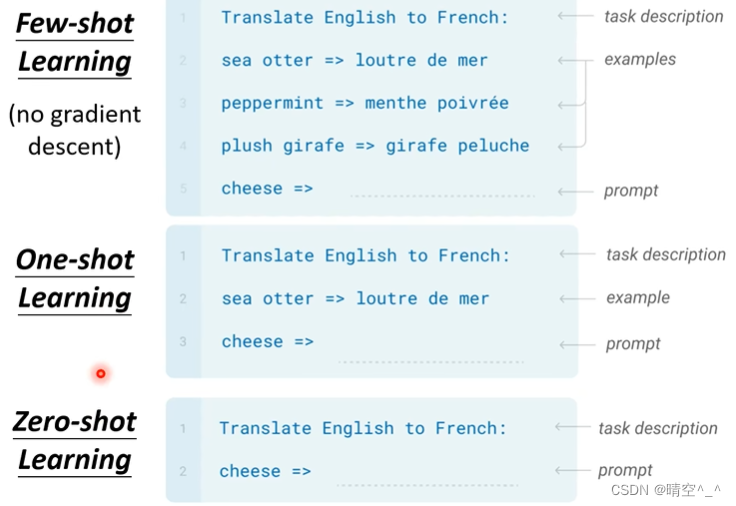
GPT-3(Language Models are Few-shot Learners)简介
GPT-3(Language Models are Few-shot Learners) 一、GPT-2 1. 网络架构: GPT系列的网络架构是Transformer的Decoder,有关Transformer的Decoder的内容可以看我之前的文章。 简单来说,就是利用Masked multi-head attention来提取文本信息&a…...
容器安全风险and容器逃逸漏洞实践
本文博客地址:https://security.blog.csdn.net/article/details/128966455 一、Docker存在的安全风险 1.1、Docker镜像存在的风险 不安全的第三方组件:用户自己的代码依赖若干开源组件,这些开源组件本身又有着复杂的依赖树,甚至…...

2023年美赛B题-重新想象马赛马拉
背景 肯尼亚的野生动物保护区最初主要是为了保护野生动物和其他自然资源资源。肯尼亚议会于2013年通过了《野生动物保护和管理法》提供更公平的资源共享,并允许替代的、以社区为基础的管理工作[1]。此后,肯尼亚增加了修正案,以解决立法中的空…...
Docker常用命令总结
目录 一、帮助启动类命令 (1)启动docker (2)停止docker (3)重启docker (4)查看docker (5)设置开机自启 (6)查看docker概要信息…...
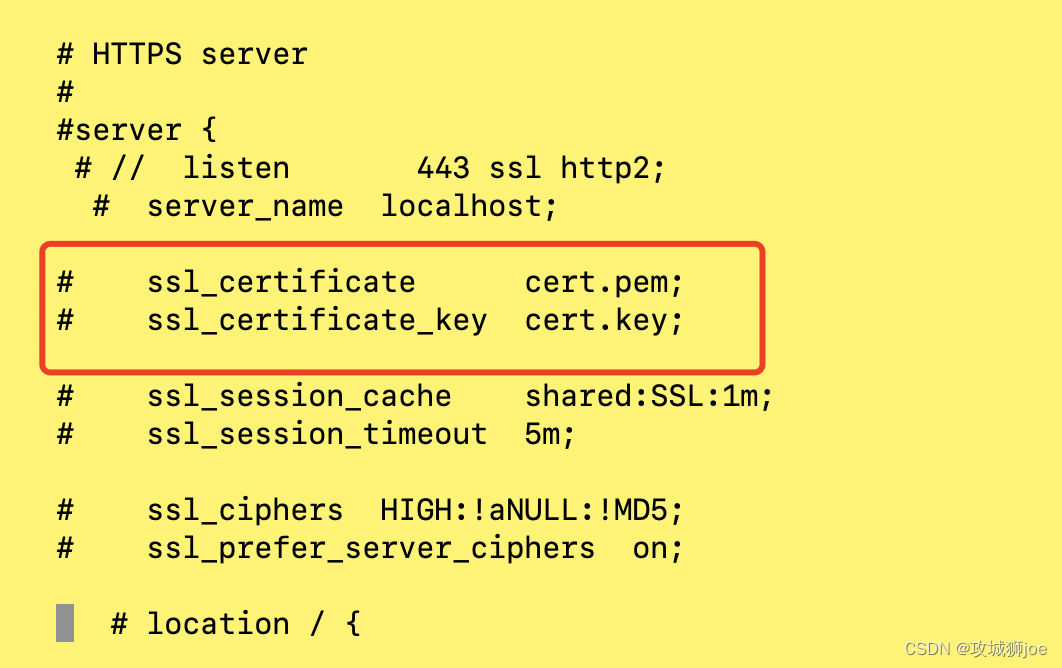
mac环境,安装NMP遇到的问题
一 背景 项目开发中,公司项目需要使用本地的环境运行,主要是php这块的业务。没有使用docker来处理,重新手动撸了一遍。记录下其中遇到的问题; 二 遇到的问题 2.1 Nginx的问题 brew install nginx后,启动nginx,报错如下:nginx: [emerg] no "ssl_certificate" …...

Web Worker 与 SharedWorker 的介绍和使用
目录一、Web Worker1 Web Worker 是什么2 Web Worker 使用3 简单示例二、SharedWorker2.1 SharedWorker 是什么2.2 SharedWorker 的使用方式2.3 多页面数据共享的例子一、Web Worker 1 Web Worker 是什么 Web Worker是 HTML5 标准的一部分,这一规范定义了一套 API…...

React:Redux和Flux
React,用来构建用户界面,它有三个特点: 作为view,构建上用户界面虚拟DOM,目的就是高性能DOM渲染【diff算法】、组件化、多端同构单向数据流,是一种自上而下的渲染方式。Flux 在一个React应用中,UI部分是由无数个组件嵌套构成的,组件和组件之间就存在层级关系,也就是父…...

TypeScript 学习之Class
基本使用 class Greeter {// 属性greeting: string;// 构造函数constructor(message: string) {// 用this 访问类的属性this.greeting message;}// 方法greet() {return Hello, this.greeting;} } // 实例化 let greeter new Greeter(World);声明了一个Greeter类ÿ…...
doris - 数仓 拉链表 按天全量打宽表性能优化
数仓 拉链表 按天全量打宽性能优化现状描述优化现状描述 1、业务历史数据可以变更 2、拉链表按天打宽 3、拉链表模型分区字段设计不合理,通用的过滤字段没有作为分区分桶字段 4、拉链表表数据量略大、模型数据分区不合理和服务器资源限制,计算任务执行超…...

服务器虚拟化及优势
服务器虚拟化是从一台物理服务器创建多个服务器实例的过程。每个服务器实例代表一个隔离的虚拟环境。在每个虚拟环境中,都可以运行单独的操作系统。 1.更有效的资源调配 使用虚拟化技术大大节省了所占用的空间,减少了数据中心里服务器和相关硬件的数量。…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...
