第十四届蓝桥杯大赛青少年省赛C++组试题真题 2023年5月
一、选择题
第 1 题 单选题
C++中,bool类型的变量占用字节数为 ( )。
A. 1
B. 2
C. 3
D. 4
第 2 题 单选题
以下关于C++结构体的说法,正确的是 ( )。
A. 结构体中只能包含成员变量,不能包含成员函数
B. 结构体不能从另一个结构体继承
C. 结构体里面可以包含静态成员变量
D. 结构体里面不能包含构造函数
第 3 题 单选题
设只含根结点的二又树高度为1,共有62个结点的完全二叉树的高度为 ( )。
A. 4
B. 5
C. 6
D. 7
第 4 题 单选题
以下关于数组的说法,不正确的是 ( ) 。
A. 数组中所有元素的类型必须都相同
B. 数组中各元素在内存中是顺序存放的
C. 数组最后一个元素的索引是数组的长度
D. 数组名的第一个字符可以是下划线
第 5 题 单选题
执行以下代码,输出的结果是( )。

A. 127
B. 97
C. 63
D. 126
二、编程题
第 6 题 问答题
特殊运算符
时间限制: 1000MS
内存限制:65536K8
题目描述
编程实现:特殊运算符
假定有一个运算符“>>>”,它的功能如下所示:
>>>257=25
>>>182=18
>>>933 =93
给定一个正整数N (100 < N < 1000) ,请计算 n-( >>> N)的结果 < /N < 1000)>
例如: N=257时,
257-(>>>257)
=257-25
=232
输入描述
输入一个正整数N (100 < N < 1000)< span> < 1000)<>
输出描述
输出一个整数,表示N -(>>>N)的结果
样例输入
257
样例输出
232
第 7 题 问答题
四叶玫瑰数
时间限制:1000MS
内存限制: 65536KB
题目描述:
编程实现: 四叶玫瑰数
四叶玫瑰数是指一个四位数,其各位上的数字的四次方之和等于本身。给定两个正整数N和M,请将N~M (1<=N<=M<=1000000)之间 (含N和M)的四叶玫瑰数按从小到大的顺序输出。
例如: N=1234,M=2345时,有一个四叶玫瑰数1634,因为1^4 +6^4 + 3^4 + 4^4 = 1634,故输出1634。
输入描述
第一行输入两个正整数N、M (1<=N<=M<=1000000)
输出描述
输出一行,包含若干个用一个空格隔开的正整数,表示N~M之间的四叶玫瑰数按从小到大的顺序的输出结果
注意:
题目数据保证给定的N~M范围内至少有一个四叶玫瑰数
样例输入
1234 2345
样例输出
1634
答案和更多内容请查看网站:
网站链接
青少年软件编程历年真题模拟题实时更新
相关文章:

第十四届蓝桥杯大赛青少年省赛C++组试题真题 2023年5月
一、选择题 第 1 题 单选题 C中,bool类型的变量占用字节数为 ( )。 A. 1 B. 2 C. 3 D. 4 第 2 题 单选题 以下关于C结构体的说法,正确的是 ( )。 A. 结构体中只能包含成员变量,不能包含成员函数 B. 结构体不能从另一个结构体继承 …...
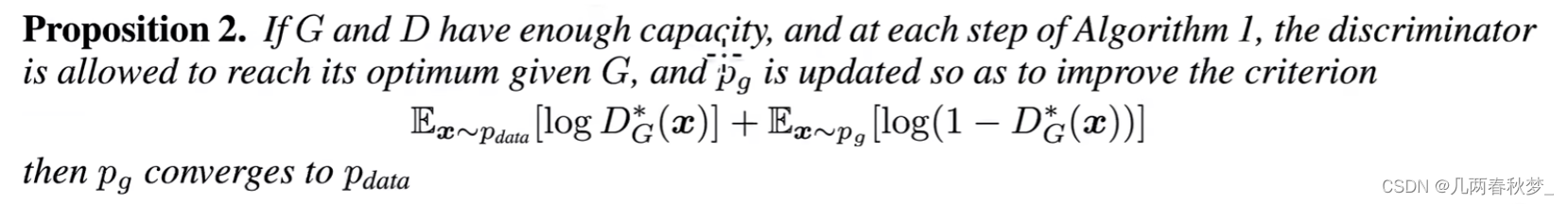
GAN论文精读
标题:Generative Adversarial Nets 摘要: 简写:作者提出了一个framework通过一个对抗的过程,在这里面会同时训练两个模型。 第一个模型为生成模型G,是用来抓住整个数据的分布 第二个模型为辨别模型D,是用来估计一个样本是否从G中产生。 …...
)
数据结构:计数排序(详解)
思路详解: 1 找到数组中的最大值、最小值 2 开辟一个统计每个数据出现次数的数组(总个数是最大值-最小值1,因为下标范围是0~最大值-最小值,闭区间统计个数要1) 3 遇到一个元素,在此元素-最小值作为下标的…...

1 请使用js、css、html技术实现以下页面,表格内容根据查询条件动态变化。
1.1 创建css文件,用于编辑style 注意: 1.背景颜色用ppt的取色器来获取: 先点击ppt的形状轮廓,然后点击取色器,吸颜色,然后再点击形状轮廓的其他轮廓颜色,即可获取到对应颜色。 2.表格间的灰色线…...
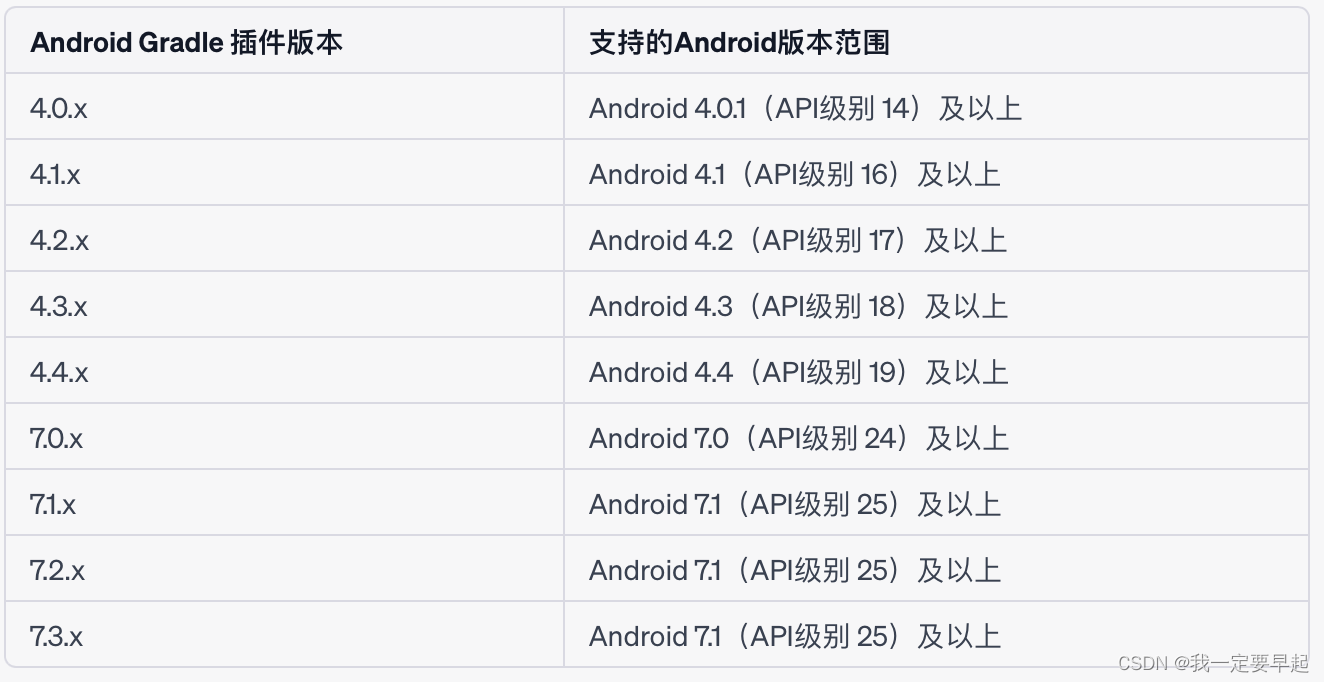
react-native项目安卓版本升级 compileSdkVersion 29->31
因为 react-native-ble-manager添加过程及碰到的问题 依赖 https://github.com/innoveit/react-native-ble-manager 参考:https://blog.csdn.net/withings/article/details/71378562 iOS 按react-native-ble-manager 文档在 【Info.plist】加了key之后能正常使用…...
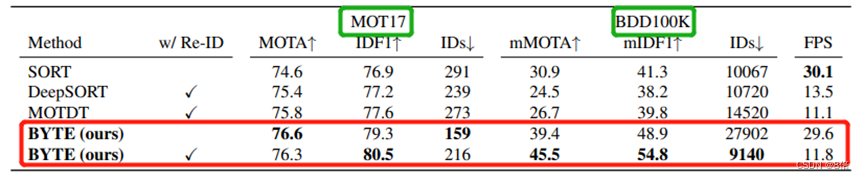
【学习笔记】目标跟踪领域SOTA方法比较
目录 前言方法1 TraDeS:2 FairMOT:3 SMILEtrack:4 ByteTrack: 前言 常用于行人跟踪的多目标跟踪数据集包括:MOT 15/16/17/20、PersonPath22等… 为更好比较现有SOTA算法的检测性能,本博客将针对在各数据集上表现较优的算法模型进行介绍。(表…...
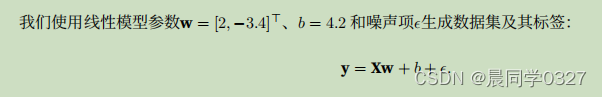
机器学习 深度学习编程笔记
sigmoid函数 def sigmoid(x):return 1.0 / (1np.exp((-x)))定义最小平方和损失函数 loss torch.nn.MSELoss()线性回归编程 如果不加噪音就成了正常的线性函数了,所以要加噪音。 torch.normal(0, 0.01, y.shape)torch.normal(0, 0.01, y.shape)是一个用于生成服从…...

18.背景轮播
背景轮播 html部分 <div class"container"><div class"slide active" style"background-image: url(./static/20180529205331_yhGyf.jpeg);"></div><div class"slide " style"background-image: url(./s…...
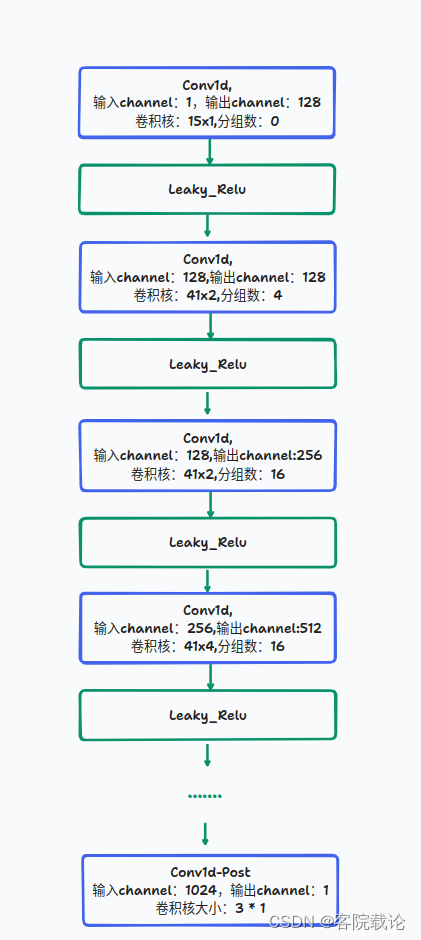
论文代码学习—HiFi-GAN(2)——鉴别器discriminator代码
文章目录 引言正文鉴别器多周期鉴定器多尺度鉴定器问题 总结 引言 这里翻译了HiFi-GAN这篇论文的具体内容,具体链接。这篇文章还是学到了很多东西,从整体上说,学到了生成对抗网络的构建思路,包括生成器和鉴定器。细化到具体实现的…...
 grep命令】)
Linux Shell 脚本编程学习之【第3章 正则表达式 (第二部分) grep命令】
第3章 正则表达式 (第二部分) 4 grep命令4.1 基本用法4.2 参考命令4.2.1 双引号4.2.2 -c 输出匹配行数4.2.3 -h 或 -l 不显示或只显示文件名4.2.4 -s 不显示错误信息4.2.5 -r 递归显示本级目录及下级目录4.2.6 -w 匹配完整词 -x 匹配完整行4.2.7 -q 退出…...
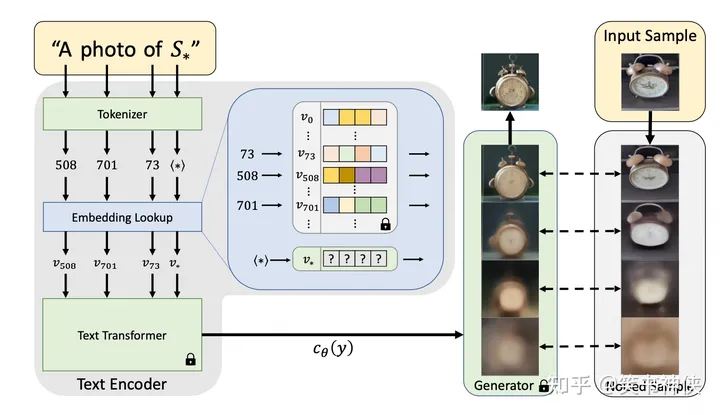
大语言模型LLM
目录 一、语言模型的发展 语言模型(Language Model,LM)目标是建模自然语言的概率分布,具体目标是构建词序列w1,w2,...,wm的概率分布,即计算给定的词序列作为一个句子出现可能的大小P(w1w2...wm)。但联合概率P的参数量…...

自学网络安全(黑客)的误区
前言 网络安全入门到底是先学编程还是先学计算机基础?这是一个争议比较大的问题,有的人会建议先学编程,而有的人会建议先学计算机基础,其实这都是要学的。而且这些对学习网络安全来说非常重要。 一、网络安全学习的误区 1.不要…...
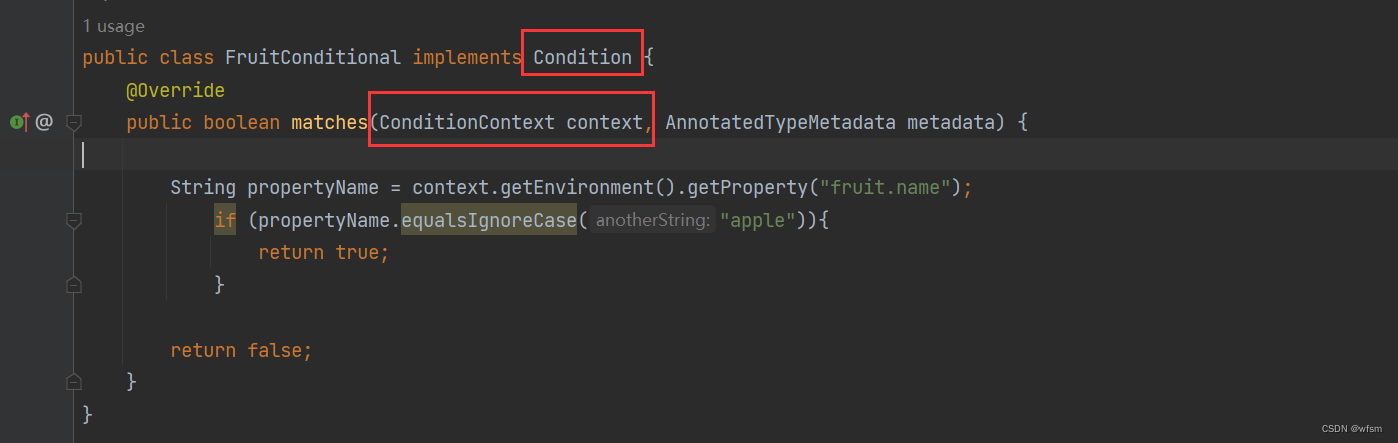
@Conditional
Conditional Conditional 是 spring framework 中提供的一个条件注解,,满足条件就注入,不满足就不注入ioc Condtional 需要和 Condition接口 一起用: 返回true注入,返回false不注入,, 里面有一…...
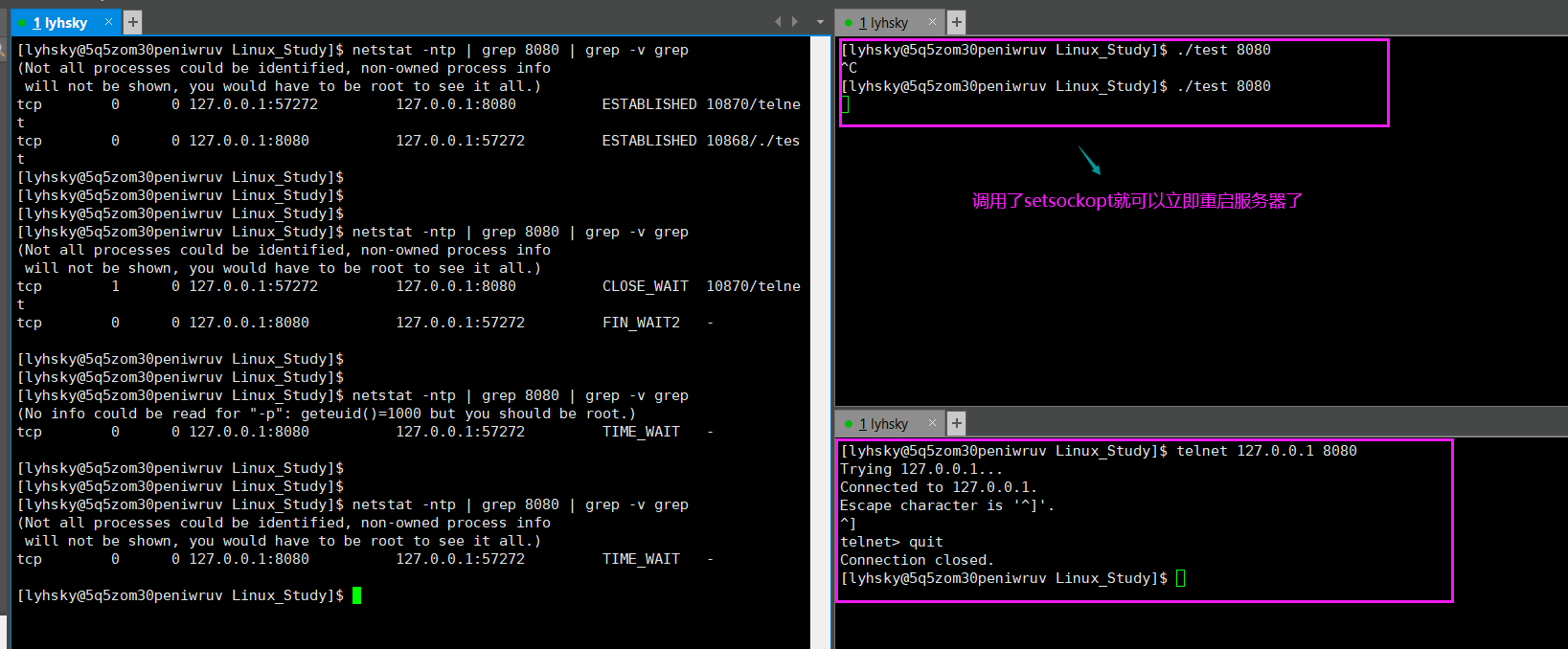
【Linux】网络基础之TCP协议
目录 🌈前言🌸1、基本概念🌺2、TCP协议报文结构🍨2.1、源端口号和目的端口号🍩2.2、4位首部长度🍪2.3、32位序号和确认序号(重点)🍫2.4、16位窗口大小🍬2.5、…...
模式)
Java设计模式之装饰器(Decorator)模式
装饰器(Decorator)设计模式允许动态地将新功能添加到对象中,同时又不改变其结构。 什么是装饰器模式 装饰器(Decorator)模式通过将对象进行包装,以扩展其功能,而不需要修改其原始类。装饰器模…...

element ui树组件render-content 树节点的内容区的渲染另一种方式
直接上代码吧,不用h的写法。 <el-tree :data"data" node-key"id" default-expand-all :expand-on-click-node"false" :props"defaultProps":render-content"renderContentTree" node-click"handleNodeClick"&g…...
html a标签换行显示
文章目录 用css display属性不用css,可以用<br>标签换行示例 用css display属性 可以使用CSS的display属性来实现多个a标签每行显示一个。 HTML代码: <div class"link-container"><a href"#">Link 1</a>…...

关于Redis-存Long取Integer类型转换错误的问题
背景 最近遇到了两个Redis相关的问题,趁着清明假期,梳理整理。 1.存入Long类型对象,在代码中使用Long类型接收,结果报类型转换错误。 2.String对象的反序列化问题,直接在Redis服务器上新增一个key-value,…...
)
设计模式一:简单工厂模式(Simple Factory Pattern)
简单工厂模式(Simple Factory Pattern)是一种创建型设计模式,它提供了一个通用的接口来创建各种不同类型的对象,而无需直接暴露对象的创建逻辑给客户端。 简单工厂的三个重要角色: 工厂类(Factory Class&…...
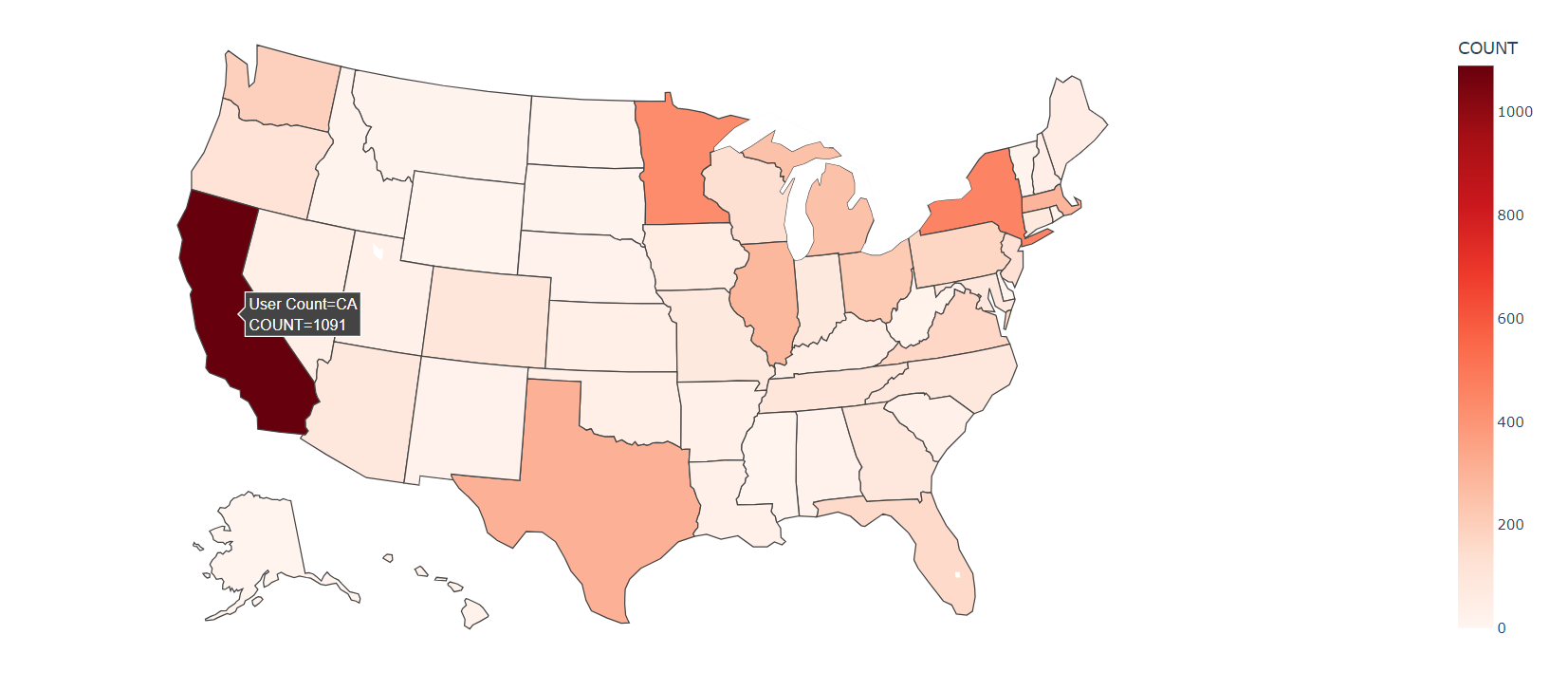
如何利用plotly和geopandas根据美国邮政编码(Zip-Code)绘制美国地图
对于我自己来说,该需求源自于分析Movielens-1m数据集的用户数据: UserID::Gender::Age::Occupation::Zip-code 1::F::1::10::48067 2::M::56::16::70072 3::M::25::15::55117 4::M::45::7::02460 5::M::25::20::55455 6::F::50::9::55117我希望根据Zip-…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...
