ETH网络学习
概要
ETH网络是一个P2P网络,整个网络又区分为“执行层”与“共识层”。“执行层”节点负责交易交换,“共识层”节点负责区块打包、区块验证、区块同步和链同步。
执行层
执行层分为“服务发现”与“DevP2P”,两者共同并行执行。
服务发现
建立在UDP协议上,通过PING-PONG方式同步执行层节点信息,PING中包含当前发现的所有节点信息,PONG理解为PING的哈希值。当节点从PING-PONG中发现新的节点,则会与新节点之间建立新的PING-PONG交互。
DevP2P
建立在TCP协议上,与其他节点进行加密通信,在权益证明的当下,DevP2P使用有线协议进行交易交换,交易交换值对等节点之间互相同步未打包交易池的交易数据。
交易执行
在当前节点的共识客户端为区块生产者时,执行层会负责选择交易池中的交易进行执行并打包,交由共识客户端记录并广播传递。
若当前节点的共识客户端不上区块生产者,执行层会从共识客户端获取交易(从其他共识客户端同步的新区块中的交易)并进行执行与验证,将验证结果返回共识客户端。
共识层
共识层也有“服务发现“,与执行层发现类似,但是有一定细节区别。
共识层通过P2P协议与其他共识层节点进行区块同步和链同步。
连接执行客户端和共识客户端
共识客户端和执行客户端并行运行。它们需要连接起来,以便共识客户端可以向执行客户端提供指令,并且执行客户端可以将交易束传递给共识客户端以包含在 Beacon 块中。两个客户端之间的通信可以使用本地RPC连接来实现。称为“Engine-API”的 API(在新选项卡中打开)↗定义两个客户端之间发送的指令。由于两个客户端都位于单个网络身份后面,因此它们共享一个 ENR(以太坊节点记录),其中包含每个客户端的单独密钥(eth1 密钥和 eth2 密钥)。
控制流摘要如下所示,相关网络堆栈位于括号中。
当共识客户端不是区块生产者时:
共识客户端通过区块八卦协议接收区块(共识 p2p)
共识客户端预先验证该块,即确保它来自具有正确元数据的有效发送者
块中的交易作为执行负载发送到执行层(本地 RPC 连接)
执行层执行交易并验证块头中的状态(即检查哈希值匹配)
执行层将验证数据传递回共识层,块现在被视为已验证(本地 RPC 连接)
共识层将块添加到自己的区块链头部并对其进行证明,通过网络广播证明(共识 p2p)
当共识客户端是区块生产者时:
共识客户端收到通知,表明它是下一个区块生产者(共识 p2p)
共识层调用create block执行客户端中的方法(本地RPC)
执行层访问已由交易八卦协议填充的交易内存池(执行p2p)
执行客户端将交易捆绑到区块中,执行交易并生成区块哈希
共识客户端从执行客户端获取交易和块哈希并将它们添加到信标块(本地 RPC)
共识客户端通过区块八卦协议广播区块(共识 p2p)
其他客户端通过区块八卦协议接收提议的区块并如上所述进行验证(共识 p2p)
一旦该块被足够的验证者证明,它就会被添加到链的头部,经过验证并最终确定。
相关文章:

ETH网络学习
概要 ETH网络是一个P2P网络,整个网络又区分为“执行层”与“共识层”。“执行层”节点负责交易交换,“共识层”节点负责区块打包、区块验证、区块同步和链同步。 执行层 执行层分为“服务发现”与“DevP2P”,两者共同并行执行。 服务发现…...

01-将函数参数化进行传递
项目源码:https://github.com/java8/ 1 应对不断变化的需求 在我们进行开发中,经常需要面临需求的不断变更,我们可以将行为参数化以适应不断变更的需求。 行为参数化就是可以帮助我们处理频繁变更的需求的一种软件开发模式 我们可以将代码…...
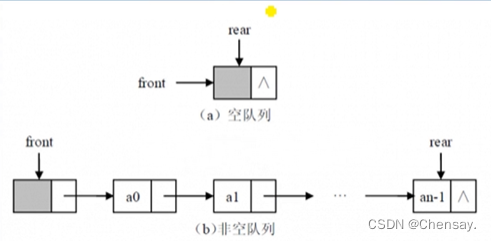
数据结构【栈和队列】
第三章 栈与队列 一、栈 1.定义:只允许一端进行插入和删除的线性表,结构与手枪的弹夹差不多,可以作为实现递归函数(调用和返回都是后进先出)调用的一种数据结构; 栈顶:允许插入删除的那端&…...
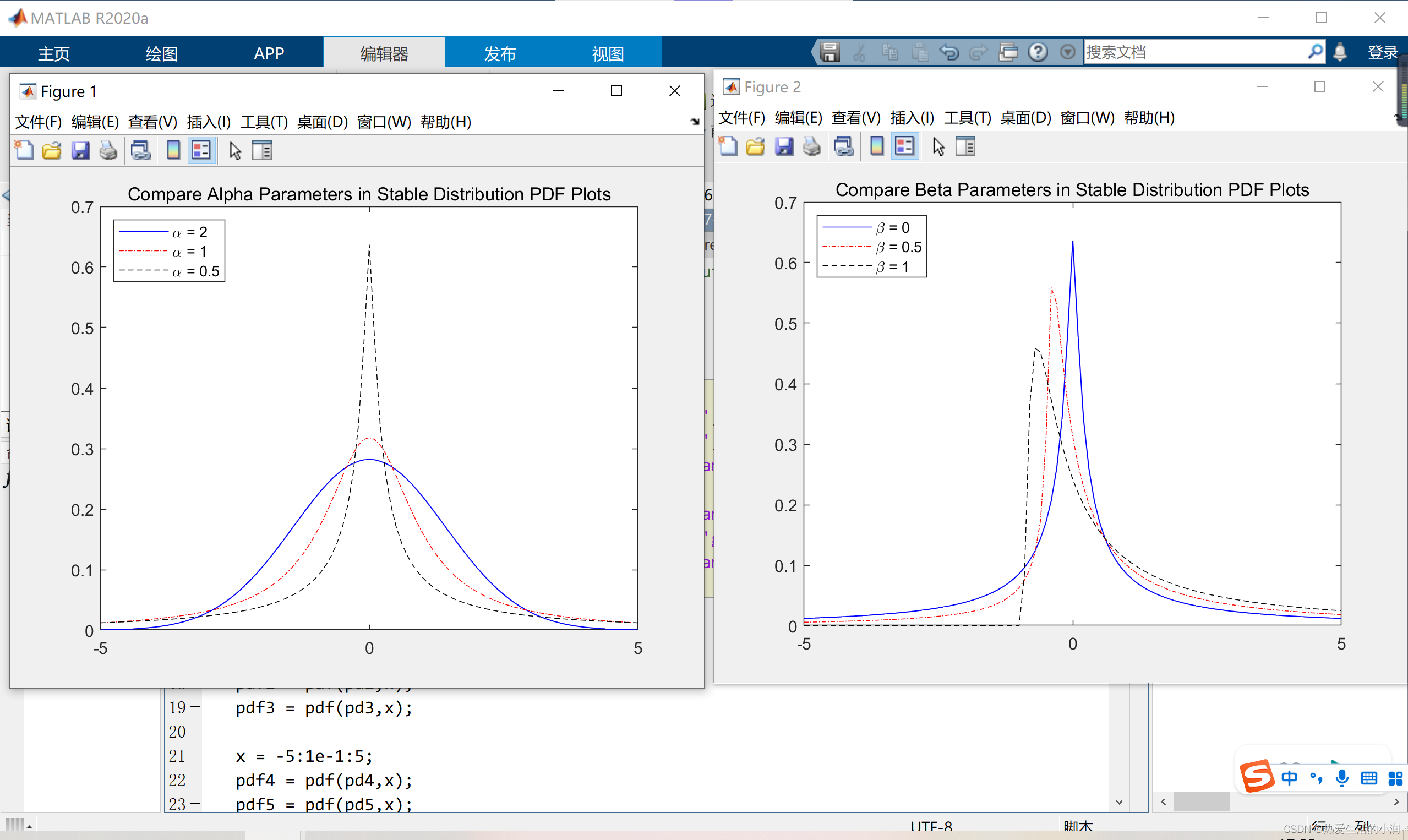
MATLAB | 产生阿尔法稳定分布噪声并作出概率密度函数
一、问题描述 想产生不同特征参数的α稳定随机变量,并且作出其概率密度函数进行对比。 二、解决思路 运行了MATLAB的官方实例代码: openExample(‘stats/ComparePDFsOfStableDistributionsExample’) (1)使用makedist()函数生成…...

深入浅出Pytorch函数——torch.softmax/torch.nn.functional.softmax
分类目录:《深入浅出Pytorch函数》总目录 相关文章: 机器学习中的数学——激活函数:Softmax函数 深入浅出Pytorch函数——torch.softmax/torch.nn.functional.softmax 深入浅出Pytorch函数——torch.nn.Softmax 将Softmax函数应用于沿dim的…...

Vue2学习笔记
vue是根据数据来构建用户界面的一套框架 创建一个vue实例 <!-- 1.创建一个容器 2.引入vue.js开发版本(全局的) 3.创建实例对象 4.配置选项 > 完成渲染 --> <div id"app">{{ msg }} </div> <script srcvue.js><…...
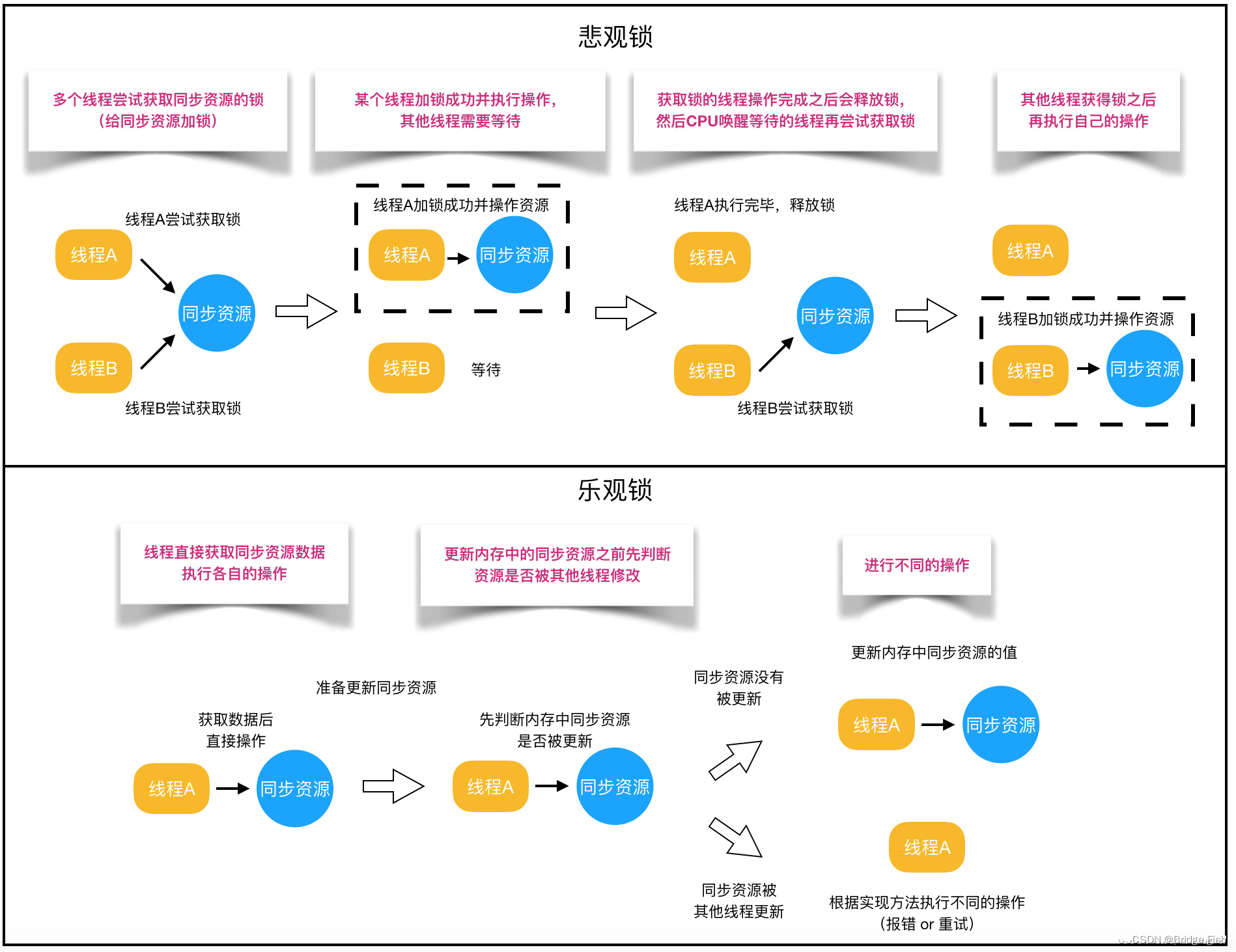
Java 悲观锁 乐观锁
锁可以从不同的角都分类。其中乐观锁和悲观锁是一种分类方式 一、悲观锁、乐观锁定义 悲观锁就是我们常说到的锁。对于悲观锁来说,他总是认为每次访问共享资源时会发生冲突,所以必须每次数据操作加上锁,以保证临界区的程序同一时间只能有一个…...
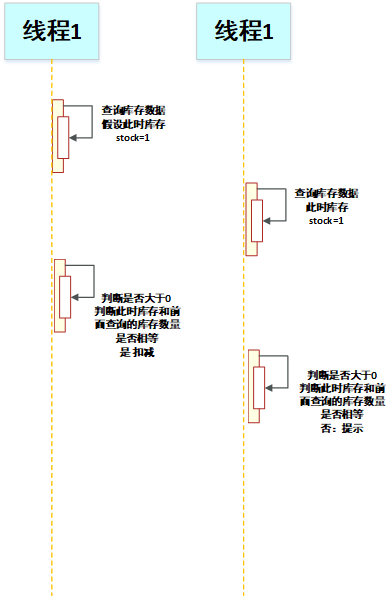
优惠券秒杀(二)
库存超卖问题分析 库存超卖问题其本质就是多个线程操作共享数据产生的线程安全问题,即当一个线程在执行操作共享数据的多条代码的过程中,其他线程也参与了进来,导致了线程安全问题的产生。例如:线程1发送请求,查询库存…...
selenium的java方式打开IE浏览器
1.下载软件Selenium Driver 官方下载地址: https://www.selenium.dev/downloads/解压selenium-java-3.141.59.zip文件到java项目 seleniumDemo,并降解压的文件放入依赖中(1)双击项目的src打开项目结构,或右键-打开…...

分类评估指标
文章目录 1. 混淆矩阵2. Precision(精准率)3. Recall(召回率)4. F1-score5. ROC曲线和AUC指标5.1 ROC 曲线5.2 绘制 ROC 曲线5.3 AUC 值6. API介绍6.1 **分类评估报告api**6.2 **AUC计算API**练习-电信客户流失预测1. 数据集介绍2. 处理流程3. 案例实现4. 小结1. 混淆矩阵 …...
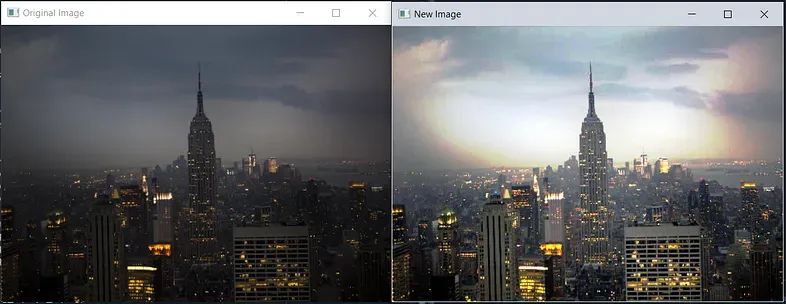
OpenCV:图像直方图计算
图像直方图为图像中像素强度的分布提供了有价值的见解。通过了解直方图,你可以获得有关图像对比度、亮度和整体色调分布的信息。这些知识对于图像增强、图像分割和特征提取等任务非常有用。 本文旨在为学习如何使用 OpenCV 执行图像直方图计算提供清晰且全面的指南。…...

用QFramework来重构 祖玛游戏
资料 Unity - 祖玛游戏 GitHub 说明 用QF一个场景就够了,在UIRoot下切换预制体达到面板切换。 但测试中当然要有一个直接跳到测试面板的 测试脚本,保留测试Scene(不然初学者也不知道怎么恢复测试Scene),所以全文按S…...

生活杂记-显示器尺寸
以下是常见显示器尺寸的对角线长度换算成厘米的结果(已经四舍五入到最接近的厘米数): 19英寸显示器 ≈ 48.26厘米21.5英寸显示器 ≈ 54.61厘米24英寸显示器 ≈ 60.96厘米27英寸显示器 ≈ 68.58厘米32英寸显示器 ≈ 81.28厘米34英寸显示器 ≈…...
)
在CSDN学Golang云原生(Kubernetes Pod无状态部署)
一,静态pod Kubernetes中的Pod是可以动态创建、销毁的,如果希望Pod只使用静态的IP地址而不是自动生成一个IP地址,那么就需要使用静态Pod。 静态Pod是在kubelet启动时通过指定文件夹路径来加载的。当kubelet检测到这些配置文件变化后&#x…...

@Bean的作用
Bean通常和Configuration注解一起使用 Bean可以用在方法上,方法返回的对象交给spring容器管理,和提供给其他程序组件使用 Bean是一个注解,用于将方法标记为Spring容器中的一个Bean。具体来说,Bean注解可以用于方法上,…...

【论文阅读22】Label prompt for multi-label text classification
论文相关 论文标题:Label prompt for multi-label text classification(基于提示学习的多标签文本分类) 发表时间:2023 领域:多标签文本分类 发表期刊:Applied Intelligence(SCI二区࿰…...

EasyExcel数据导出功能封装
起因: 最近需要用到excel导出功能,使用EasyExcel可以快速实现导出,又需要优雅的对EasyExcel进行封装,在实现自己的导出功能时又可以制定一定的规则,让其他同事方便使用,最近研究了下网上的常规写法,站在巨人的肩上重新添加了自己的思路,供大家参考,有任何问题请多指教…...
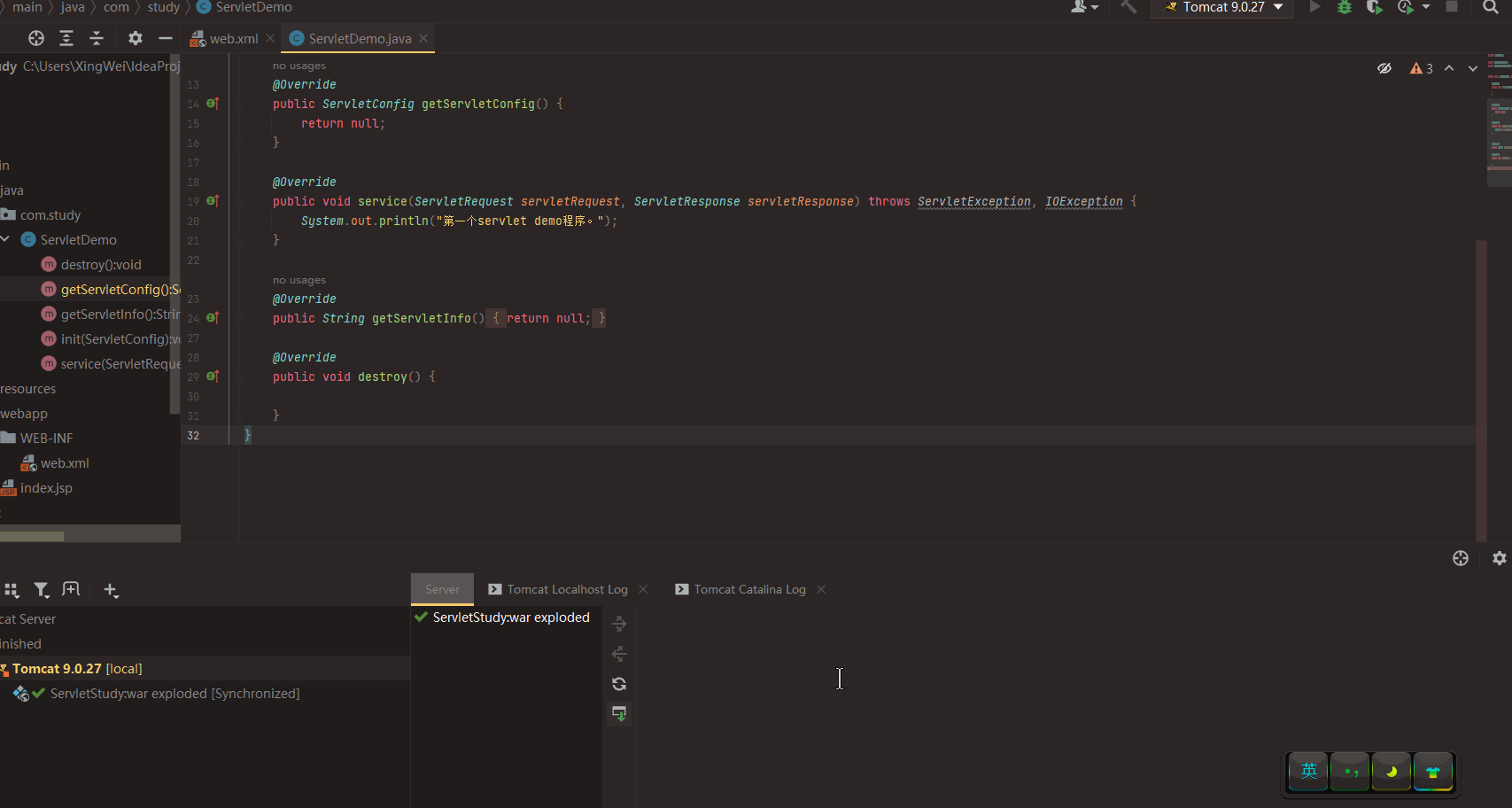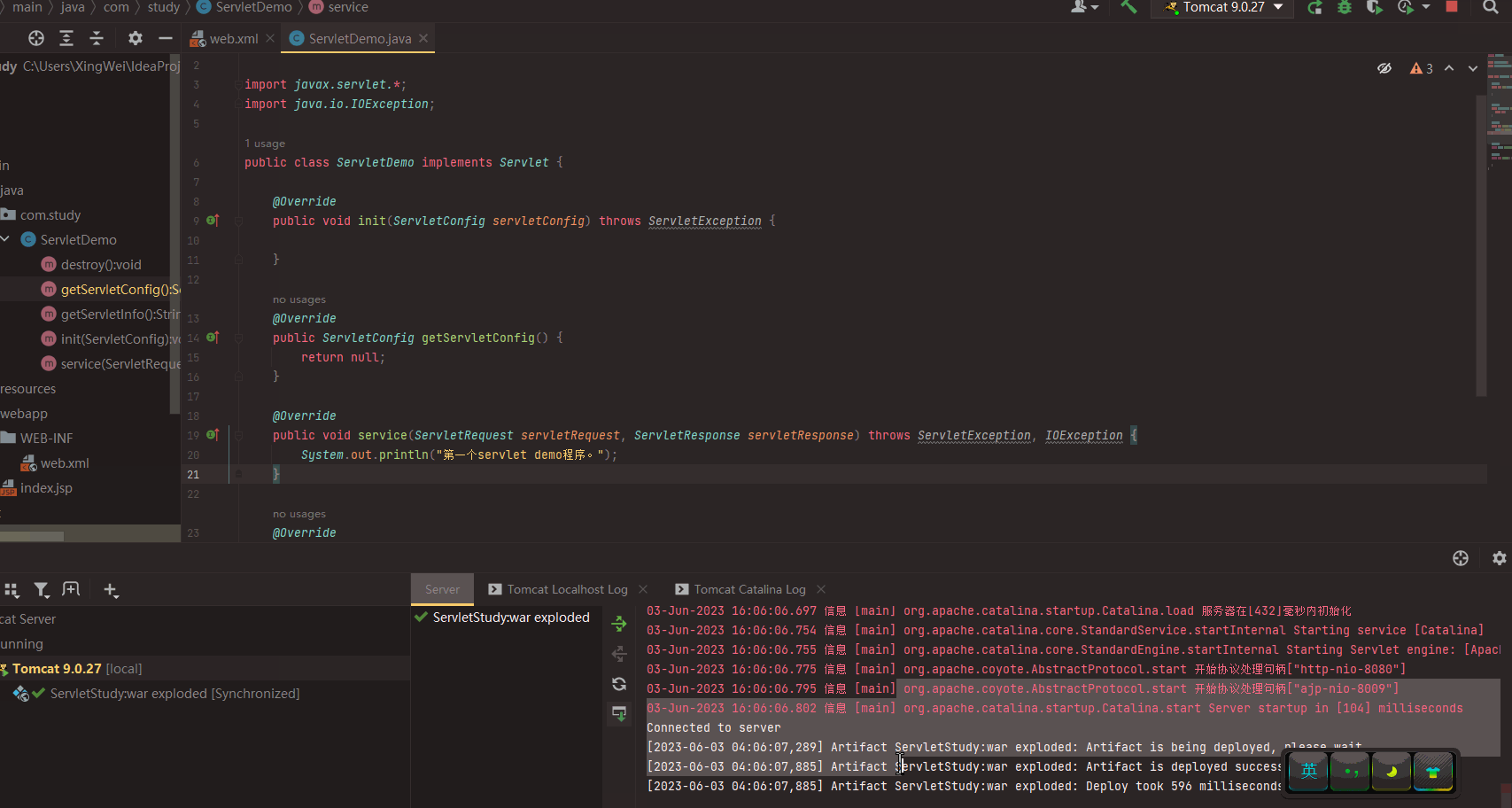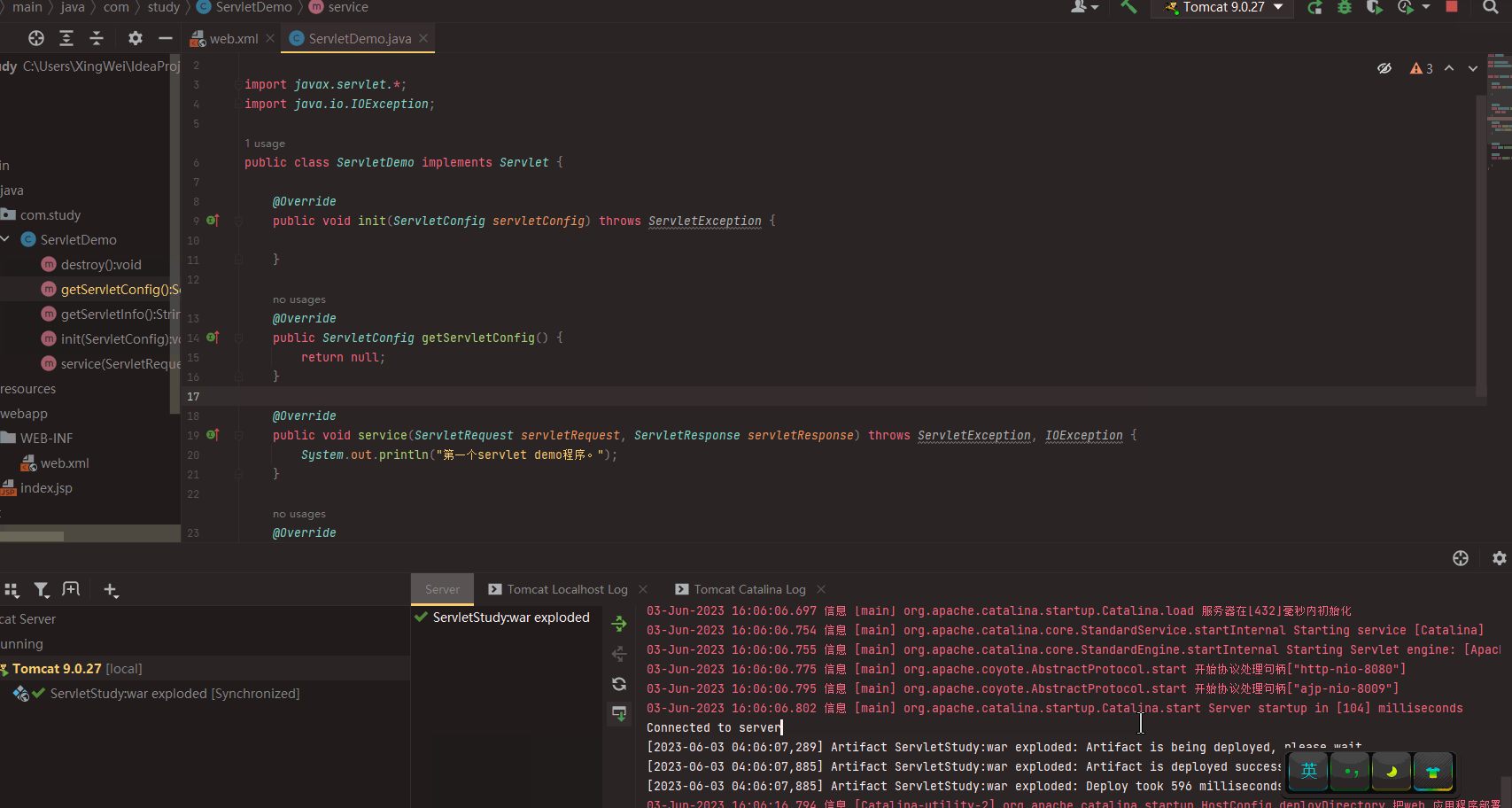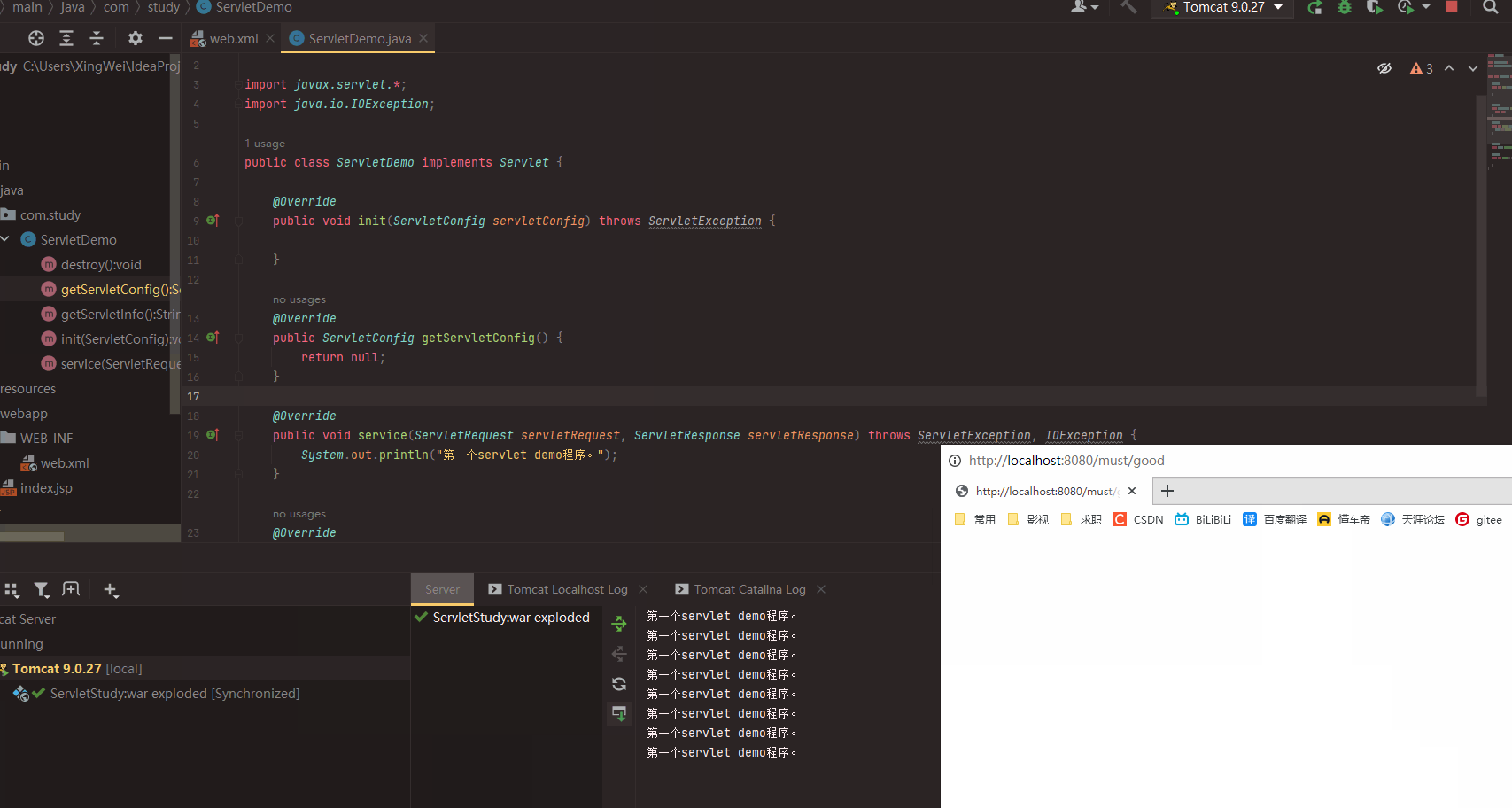
通过web.xml来配置servlet程序
IDEA 2022.3.3 tomcat-9.0.27 Java EE8 JDK-16 配置访问的虚拟路径 web.xml <?xml version"1.0" encoding"UTF-8"?> <web-app xmlns"http://xmlns.jcp.org/xml/ns/javaee"xmlns:xsi"http://www.w3.org/2001/XMLSchema-insta…...
umi 创建的项目中,如何配置多个环境变量
创建env.js 在config.js中配置 在页面中使用 env.js和config.js的目录顺序 package.json中的配置...

Mysql 5.7 连接数爆满 清理连接数
Mysql 5.7 连接数爆满 清理连接数 我在做项目的时候遇到了这个报错,然后搜了半天也没有在网上找到mysql清理连接数的方案,后面还是自己写了一个 打开MySQL命令行或客户端,并使用管理员权限登录到MySQL服务器。 我这里使用的是navicat 输入…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...
