【C语言进阶篇】指针都学完了吧!那回调函数的应用我不允许还有人不会!

文章目录
- 📋 前言
- 💬 函数指针数组
- 💭 函数指针数组的定义
- 💭 函数指针数组的应用 —— 转移表
- 💻 代码改进
- 💬 指向函数指针数组的指针
- 💬 回调函数
- 💭 利用回调函数进行代码改进
- 📝全篇总结
📋 前言
🌈hello! 各位宝子们大家好啊,上节课我们学习了函数指针,而函数指针有一个非常大的用途就是实现回调函数!
⛳️在了解回调函数之前我们还需要学习一下函数指针数组的概念!
📚本期文章收录在《C语言进阶篇》,大家有兴趣可以看看呐!
⛺️ 欢迎铁汁们 ✔️ 点赞 👍 收藏 ⭐留言 📝!
🔥 注:VS2022 等C语言学习工具都在《学习工具专栏》, 还有各种实用调试技巧有兴趣可以去看看!
💬 函数指针数组
⛳️既然我们有指针数组的概念,那么函数本身也是一个地址啊!函数指针数组 和 指针数组只不过多了函数俩字 ,那么函数指针数组该如何定义呢?
💭 函数指针数组的定义
⛳️假设我们要写一个计算器,加减乘除4个部分的函数但是函数参数都是一样的。想把他放到一个函数指针数组里面该怎么办呢?
- 函数指针我们知道怎么定义但是,加了数组俩字该怎么定义呢?
📚 代码演示:
#include <stdio.h>int Sum(int x, int y)
{return x + y;
}
int Sub(int x, int y)
{return x - y;
}
int Mul(int x, int y)
{return x * y;
}
int Div(int x, int y)
{return x / y;
}int main()
{int (*pf1)(int, int) = Sum;int (*pf2)(int, int) = Sub;int (*pf3)(int, int) = Mul;int (*pf4)(int, int) = Div;//函数指针数组int (*pfArr[4])(int, int) = {Sum,Sub,Mul,Div};return 0;
}
大家看函数指针数组就是这样定义的,由于【】号的结合性比 * 号高所以 pfArr就先和【】号结合,所以pfArr[ 4 ] 表示这个指针是个数组。
*号则代表pfArr[ 4 ] 是个指针- int(*)(int , int ) 代表了他是个函数指针类型的
- 所以 nt (*pfArr[4])(int, int) 是函数指针数组类型的
💭 函数指针数组的应用 —— 转移表
前面写的计算器,如果按照我们以前思路写的代码会非常冗余,那么我们学了函数指针数组有没有可能吧代码优化下嘛?
- 这时就要用到函数指针数组的应用 —— 转移表了
- 我们来看一下:
📚 未改变前:
#include <stdio.h>int Sum(int x, int y)
{return x + y;
}
int Sub(int x, int y)
{return x - y;
}
int Mul(int x, int y)
{return x * y;
}
int Div(int x, int y)
{return x / y;
}void menu()
{printf("***********************\n");printf("***** 1:add 2:sub ***** \n");printf("***** 3:mul 4:div *****\n");printf("***** 0.exit *****\n");printf("***********************\n");
}
int main()
{int input = 0;int x = 0;int y = 0;int ret = 0;do{menu();printf("请输入->");scanf("%d", &input);switch (input){case 1:printf("请输入俩个操作数:");scanf("%d %d", &x, &y);ret = Sum(x, y);printf("%d\n", ret);break;case 2:printf("请输入俩个操作数:");scanf("%d %d", &x, &y);ret = Sub(x, y);printf("%d\n", ret);break;case 3:printf("请输入俩个操作数:");scanf("%d %d", &x, &y);ret = Mul(x, y);printf("%d\n", ret);break;case 4:printf("请输入俩个操作数:");scanf("%d %d", &x, &y);ret = Div(x, y);printf("%d\n", ret);break;case 0:printf("退出计算器!\n");break;default:printf("选择错误,请重新输入!\n");break;}} while (input);return 0;
}
💻 代码改进
这里我们就带代码进行了改进,使得main() 函数里面代码量大大减少。
- 这里由于我们选择时的数字要和数组下标一样
- 所以我们填充一个空指针
NULL让每个数组下标和我们的操作数对应!
#include <stdio.h>
int Sum(int x, int y)
{return x + y;
}
int Sub(int x, int y)
{return x - y;
}
int Mul(int x, int y)
{return x * y;
}
int Div(int x, int y)
{return x / y;
}void menu()
{printf("***********************\n");printf("***** 1:add 2:sub ***** \n");printf("***** 3:mul 4:div *****\n");printf("***** 0.exit *****\n");printf("***********************\n");
}
int main()
{int input = 0;int x = 0;int y = 0;int ret = 0;do{menu();printf("请输入->");scanf("%d", &input);//函数指针数组 —— 转移表int(*pfArr[5])(int, int) = {NULL ,Sum,Sub,Mul,Div};if (input >= 1 && input <= 4){printf("请输入操作数:");scanf("%d %d", &x, &y);ret = pfArr[input](x, y);printf("%d\n", ret);}else if (input == 0){return 0;}else{printf("选择错误请重新输入;\n");}} while (input);return 0;
}
💬 指向函数指针数组的指针
这里我们又进行了一遍套娃,指针数组既然我们能接收那么。有没有指向函数指针数组的指针呢?答案是有的。
- 数组指针类型 int (*p)[ 5 ]
- 函数指针类型 int (*pf)(int, int)
- 函数指针数组类型 int (*pf [ 5 ])(int, int)
- 指向函数指针数组的指针 int (*(*pf)[ 5 ])(int, int)
这里我们可以怎么样理解呢?首先在指向函数指针数组的指针不要硬写在我们函数指针数组的类型上进行改变!
- 函数指针数组类型 int (*pf [ 5 ])(int, int)
- 我们首选需要一个指向函数指针数组的指针
- 那么pf 就不能和左边的
*结合 因为 int (* [ 5 ])(int, int) 代表了函数指针数组类型而我们想要接收他就需要一个指针 *pf - 那么把它括起来就是指向函数指针数组的指针了
- int (*(*pf)[ 5 ])(int, int)
📚 代码演示:
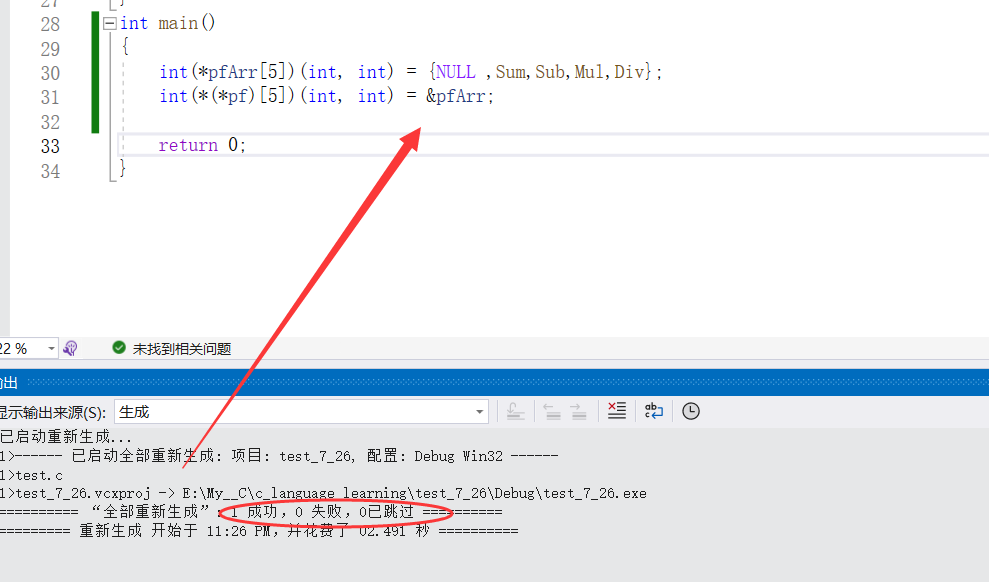
💬 回调函数
⛳️回调函数就是一个通过函数指针调用的函数。如果你把函数的指针(地址)作为参数传递给另一个函数,当这个指针被用来调用其所指向的函数时,我们就说这是回调函数。回调函数不是由该函数的实现方直接调用,而是在特定的事件或条件发生时由另外的一方调用的,用于对该事件或条件进行响应。
- 怎么应用呢?函数指针的应用其实就是回调函数
- 我们前面改进计算器的的时候用函数指针数组进行改进
- 那么我们下面就对计算器用回调函数的方式进行改进
回调函数我的理解就是通过函数指针的方式接收函数的地址,从而调用它。让一个函数可以调用多个同类型的函数的功能在特定的情况给我传输函数地址从而使用它。
- 上面计算器的实现用switch 语句实现的时候每一个case语句都是相同的除了函数的实现方法不同。这样就导致代码过于冗余!
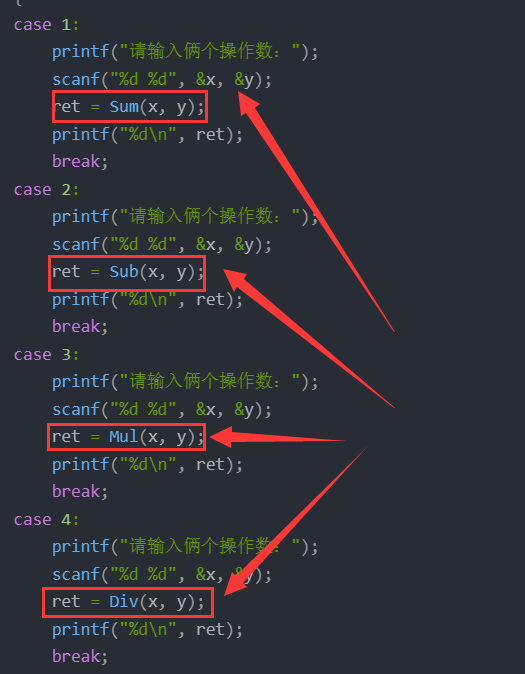
而这我们就可以用一个回调函数进行改进,让这些代码都在一个函数里面。每次使用那个函数直接传送给我们的地址就行了!
📚 代码演示:
这样铁汁们看是不是就避免的代码冗余的问题,我们只需要把函数地址传过来就可以了,输入什么选择就传什么函数从而去调用他!
void calc(int (*pf)(int x, int y))
{int x = 0;int y = 0;printf("请输入操作数;");scanf("%d %d", &x, &y);int ret = pf(x, y);printf("%d\n", ret);
}
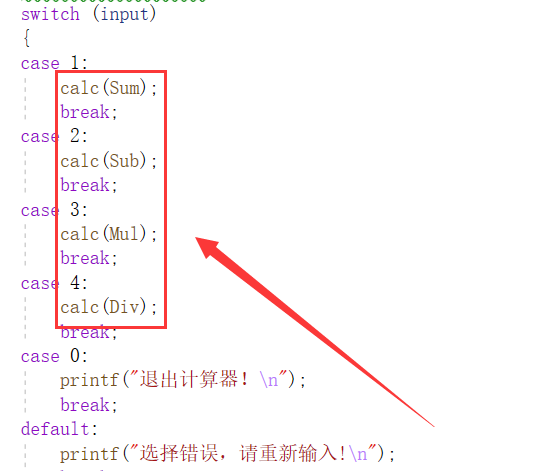
💭 利用回调函数进行代码改进
📚 代码演示:
#include <stdio.h>
int Sum(int x, int y)
{return x + y;
}
int Sub(int x, int y)
{return x - y;
}
int Mul(int x, int y)
{return x * y;
}
int Div(int x, int y)
{return x / y;
}void menu()
{printf("***********************\n");printf("***** 1:add 2:sub ***** \n");printf("***** 3:mul 4:div *****\n");printf("***** 0.exit *****\n");printf("***********************\n");
}
void calc(int (*pf)(int x, int y))
{int x = 0;int y = 0;printf("请输入操作数;");scanf("%d %d", &x, &y);int ret = pf(x, y);printf("%d\n", ret);
}
int main()
{int input = 0;do{menu();printf("请输入->");scanf("%d", &input);switch (input){case 1:calc(Sum);break;case 2:calc(Sub);break;case 3:calc(Mul);break;case 4:calc(Div);break;case 0:printf("退出计算器!\n");break;default:printf("选择错误,请重新输入!\n");break;}} while (input);return 0;
}
📝全篇总结
✅ 归纳:
好了以上就是回调函数的使用和讲解以及函数指针数组的概念大家好好理解一下吧!
函数指针数组
函数指针数组的使用
回调函数的概念
回调函数的应用
☁️ 好了今天的知识全是干货不知道各位铁汁们学到了没有呢!快拿去用吧!
看到这里了还不给博主扣个:
⛳️ 点赞☀️收藏 ⭐️ 关注!
💛 💙 💜 ❤️ 💚💓 💗 💕 💞 💘 💖
拜托拜托这个真的很重要!
你们的点赞就是博主更新最大的动力!
有问题可以评论或者私信呢秒回哦。

相关文章:

【C语言进阶篇】指针都学完了吧!那回调函数的应用我不允许还有人不会!
🎬 鸽芷咕:个人主页 🔥 个人专栏:《C语言初阶篇》 《C语言进阶篇》 ⛺️生活的理想,就是为了理想的生活! 文章目录 📋 前言💬 函数指针数组💭 函数指针数组的定义💭 函数指针数组的…...
专注:如何提高专注力和注意力的简要指南
专注力和集中力可能很难掌控的很好。大多数人都想学习如何提高注意力和注意力。但真的做到了?我们生活在一个嘈杂的世界里,不断的分心会使注意力难以集中。 此指南包含有关如何获得并保持专注的研究。我们将分解提升您的思维并关注重要事物背后的理论依…...
Linux查看内存的几种方法
PS的拼接方法 ps aux|head -1;ps aux|grep -v PID|sort -rn -k 4|head 进程的 status 比如说你要查看的进程pid是33123 cat /proc/33123/status VmRSS: 表示占用的物理内存 top PID:进程的ID USER:进程所有者 PR:进程的优先级别&#x…...
selenium定位rect元素
rect元素属性 rect元素的属性如下: x:此属性确定矩形的x坐标。 值类型:| ; 默认值:0 动画:是y:此属性确定矩形的y坐标。 值类型:| ; 默认值:0 动画:是width:…...

uniapp <textarea>组件的踩坑
1、ios真机上,textarea输入时会触发页面其他点击事件, 解决方法:把textarea封装成基础组件,绕过这个bug。 2、使用auto-height属性,安卓真机上,会导致textarea高度异常, 官方人员解释…...

README.md 文档使用 treer 生成树形项目结构
一、前言 前后端编写 README.md 文档的时候,常常需要描写项目的结构,使用 tree 命令生成的目录又不能忽略某个目录,不方便。后来我找到了可以忽略某些目录的 treer命令 ,特此记录一下: 二、使用 treer 生成项目结构 全局安装tr…...
朝花夕拾思维导图怎么画?看看这种绘制方法
朝花夕拾思维导图怎么画?绘制思维导图的好处有很多,首先它可以帮助人们更好地组织和管理知识,提高工作效率和学习效果。其次,绘制思维导图可以帮助人们更好地记忆知识点和理解知识点。总之,绘制思维导图可以帮助人们更…...

Python - OpenCV、OCR识别摄像头中的文字
使用Python3的OpenCV库来识别摄像头中的文字,以及使用OCR(光学字符识别)技术。 安装OpenCV库 在命令行中输入以下命令来安装OpenCV库: pip install opencv-python安装Tesseract OCR库 Tesseract OCR库是一种免费的光学字符识别…...
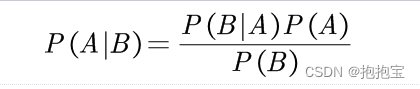
金融中的数学:贝叶斯公式
1.贝叶斯定理 贝叶斯定理是概率论中的一项重要定理,用于在已知某一事件的条件下,求另一事件发生的概率。它是根据条件概率推导出来的,得名于英国数学家托马斯贝叶斯。 贝叶斯定理可以表示为: 这个式子就是贝叶斯公式,…...
ClickHouse单节点安装配置
四个安装包: 创建clickhouse目录 将安装包解压到该目录 tar -zxvf clickhouse-server-21.9.4.35.tgz -C /opt/module/clickhouse tar -zxvf clickhouse-common-static-21.9.4.35.tgz -C /opt/module/clickhouse tar -zxvf clickhouse-common-static-dbg-21.9.4.35.…...
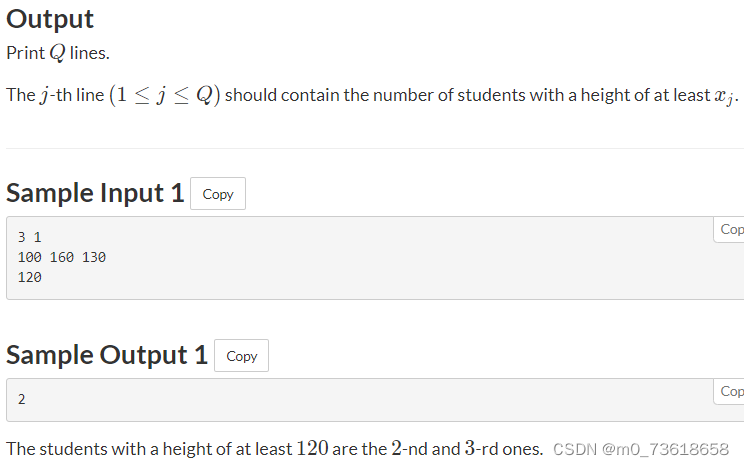
AtcoderABC231场
A - Water PressureA - Water Pressure 题目大意 假设水压仅取决于深度,在深度为x米时,水压为x/100兆帕斯卡。 现在给定一个深度D米,需要计算在该深度下的水压是多少兆帕斯卡。 思路分析 直接将输入的深度除以100得到水压结果。 时间复杂…...

opengauss数据库快速安装
root执行 groupadd gs useradd -g gs gs passwd gs mkdir -p /opt/software/openGauss sudo chown gs:gs /opt/software/openGauss chmod 700 /opt/software/openGauss gs执行 上传文件到/home/gs目录下 tar -jxf openGauss-x.x.x-openEuler-64bit.tar.bz2 -C /opt/software/o…...

前端中的LocalStorage和SessionStorage
在前端开发中,常常需要在浏览器端保存数据,以便在页面刷新或跳转时能够保留数据或状态。在这种情况下,可以使用Web Storage API中的LocalStorage和SessionStorage来实现数据的存储。它们都是HTML5提供的本地存储解决方案,可以在浏…...
论文工具——写论文好用的绘图工具(甘特图+流程图+网络模型图+泳道图)
文章目录 引言正文手动画图的在线画图工具tldraw开源免费ProcessOnDraw.io 网络模型图工具NN-SVG设置参数自动生成Netron上传模型自动生成PlotNeuralNet编码生成 总结 引言 在写HiFi-GAN论文的代码阅读过程中,我发现仅仅通过文字来描述网络结构,不够详细…...

Vite构建的vue3项目修改网站标题和图标
1.准备一张.ico后缀的图片,这里推荐文件转换器,可以将常见的图片格式转为.ico格式图片。 2.修改网站标题和图标 网站的标题和图标都可以在项目根路径下的index.html下修改。 2.1 网站标题修改<title>标签体内容即可。 2.2 网站图标修改如图<…...

平安私人银行受邀慈善服务高质量发展会议,分享慈善规划服务
近日,中华慈善总会家风传承与慈善信托委员会成立仪式,以及由中华慈善总会、中国银行业协会联合发起的“慈善顾问赋能计划”启动仪式在北京举行。平安私人银行受邀参会并分享慈善规划服务,平安私人银行慈善业务总监王英及平安私人银行客户、“…...

MySQL主从复制、读写分离
一、前言二、主从复制原理2.1 MySQL复制类型2.2 MySQL主从复制工作过程2.3 MySQL的四种同步方式2.3.1 异步复制(MySQL默认)2.3.2 同步复制2.3.3 半同步复制(企业常用)2.3.4 增强半同步复制 2.4 MySQL主从复制延迟原因和优化方法2.…...
Redis配置与优化
目录 一、关系数据库与非关系型数据库 1、关系型数据库 2、非关系型数据库 3、关系型数据库和非关系型数据库区别 1、数据存储方式不同 2、扩展方式不同 3、对事务性的支持不同 二、Redis 1、简介 2、优点 3、缺点 4、使用场景 5、哪些数据适合放入缓存中 6、为什…...

leetCode刷题记录3-面试经典150题
文章目录 不要摆,没事干就刷题,只有好处,没有坏处,实在不行,看看竞赛题面试经典 150 题80. 删除有序数组中的重复项 II189. 轮转数组122. 买卖股票的最佳时机 II 不要摆,没事干就刷题,只有好处&…...
MySQL优化(面试)
文章目录 通信优化查询缓存语法解析及查询优化器查询优化器的策略 性能优化建议数据类型优化索引优化 优化关联查询优化limit分页对于varchar end mysql查询过程: 客户端向MySQL服务器发送一条查询请求服务器首先检查查询缓存,如果命中缓存,则立刻返回存…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...
