21.2:象棋走马问题
请同学们自行搜索或者想象一个象棋的棋盘,
然后把整个棋盘放入第一象限,棋盘的最左下角是(0,0)位置
那么整个棋盘就是横坐标上9条线、纵坐标上10条线的区域
给你三个 参数 x,y,k
返回“马”从(0,0)位置出发,必须走k步
最后落在(x,y)上的方法数有多少种?
一:暴力方法
/*** 暴力方法*/public static int jump(int a, int b, int k) {return process(a, b, k, 0, 0);}//返回落在a,b上并且走k步的方法数public static int process(int a, int b, int k, int x, int y) {if (k == 0) {return (x == a && y == b) ? 1 : 0;}//9行10列if (x < 0 || y < 0 || x > 9 || y > 8) {return 0;}int p1 = process(a, b, k - 1, x + 2, y + 1);int p2 = process(a, b, k - 1, x + 1, y + 2);int p3 = process(a, b, k - 1, x + 2, y - 1);int p4 = process(a, b, k - 1, x + 1, y - 2);int p5 = process(a, b, k - 1, x - 2, y + 1);int p6 = process(a, b, k - 1, x - 1, y + 2);int p7 = process(a, b, k - 1, x - 2, y - 1);int p8 = process(a, b, k - 1, x - 1, y - 2);return p1 + p2 + p3 + p4 + p5 + p6 + p7 + p8;}
表格法
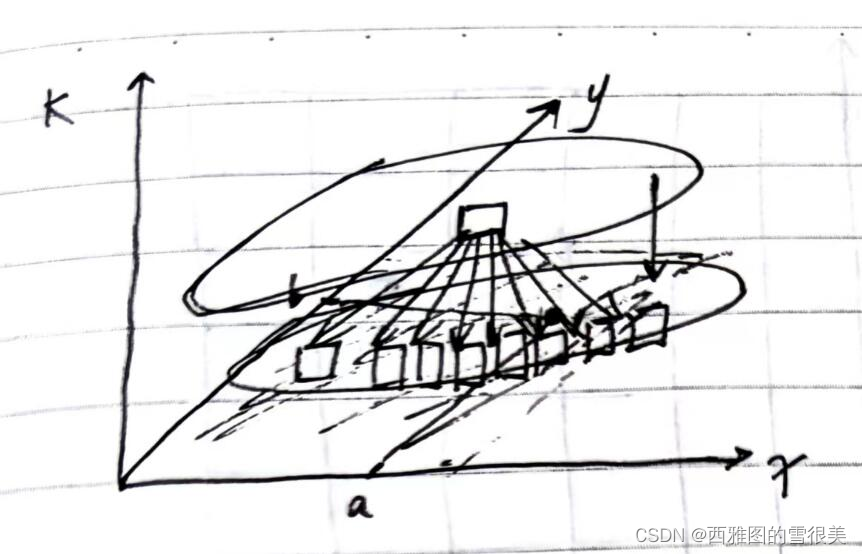
有三个变化的变量分别是:x,y,k 所以是一个三维的表格。
当层数是0的时候,只有(a,b,0)处是1,其他位置是0。
我还发现上一层是严格的依赖下一层的。上一层的每一个表格严格依赖下一层对应的八个表格(不越界的话)。
那填表的顺序就是由下往上一层一层的填表。
注意最后返回的是:dp[][][][] [ 0 ] [ 0 ] [ k ] 而不是 dp[][][][] [ a ] [ b ] [ k ] —> 表格法可以看成是递归的归过程。最终归的终点是最开始传入
进方法的起点位置。
本题可以想象一下:刚开始一定是(0,0,k) 之后向下层依赖,辐射到下一层的8个位置(不越界),之后下一层的8个位置继续向下层辐射8个位置,直到辐射到最底层,如果辐射到的最低层包含着(a,b,0)就算可以到达目标位置。
/*** 迭代法*/public static int dp(int a, int b, int k) {//这里需要考虑k以及k==0时的情况,所以取k的范围是k+1个int[][][] dp = new int[10][9][k + 1];//依赖关系是:上层依赖下层,最终返回最上层,所以从下向上构建dp[a][b][0] = 1;for (int plie = 1; plie <= k; plie++) {//这一层的每个数都依赖下一层。for (int x = 0; x < 10; x++) {for (int y = 0; y < 9; y++) {int p1 = pick(dp, x + 2, y + 1, plie - 1);int p2 = pick(dp, x + 1, y + 2, plie - 1);int p3 = pick(dp, x + 2, y - 1, plie - 1);int p4 = pick(dp, x + 1, y - 2, plie - 1);int p5 = pick(dp, x - 2, y + 1, plie - 1);int p6 = pick(dp, x - 1, y + 2, plie - 1);int p7 = pick(dp, x - 2, y - 1, plie - 1);int p8 = pick(dp, x - 1, y - 2, plie - 1);dp[x][y][plie] = p1 + p2 + p3 + p4 + p5 + p6 + p7 + p8;}}}return dp[0][0][k];//注意返回的是(0,0,k)这个坐标}public static int pick(int[][][] dp, int x, int y, int pile) {if (x < 0 || y < 0 || x > 9 || y > 8) {return 0;} else {return dp[x][y][pile];}}
相关文章:

21.2:象棋走马问题
请同学们自行搜索或者想象一个象棋的棋盘, 然后把整个棋盘放入第一象限,棋盘的最左下角是(0,0)位置 那么整个棋盘就是横坐标上9条线、纵坐标上10条线的区域 给你三个 参数 x,y,k 返回“马”从(0,0)位置出发,必须走k步 …...

【CSS】手写 Tooltip 提示组件
文章目录 效果示例代码实现 效果示例 代码实现 <!DOCTYPE html> <html><head><meta charset"utf-8"><title>一颗不甘坠落的流星</title><style>body {padding: 120px;}.tooltip {position: relative;display: inline-blo…...

MySQL DDL语法
MySQL DDL语法 DDL简介 MySQL DDL(Data Definition Language)是用于定义和管理数据库结构的语言。它包括创建、修改和删除数据库、表、视图、索引和其他数据库对象的语句。DDL语法的重要性如下: 数据库结构定义:DDL语句用于创建…...

Git 绑定账号 和clone
一:环境: 下载安装完成Git,在桌面或文件夹下(在你将要保存代码的位置)右击可以看到Git Bash Here,点击可以进入黑窗口 二:配置公钥 1.查看当前状态(如果已绑定,且知道密码可以登陆,可以直接获取SSH公钥并配置即可拉取代码) git config --list 2.配置全局git用户名和邮箱 …...
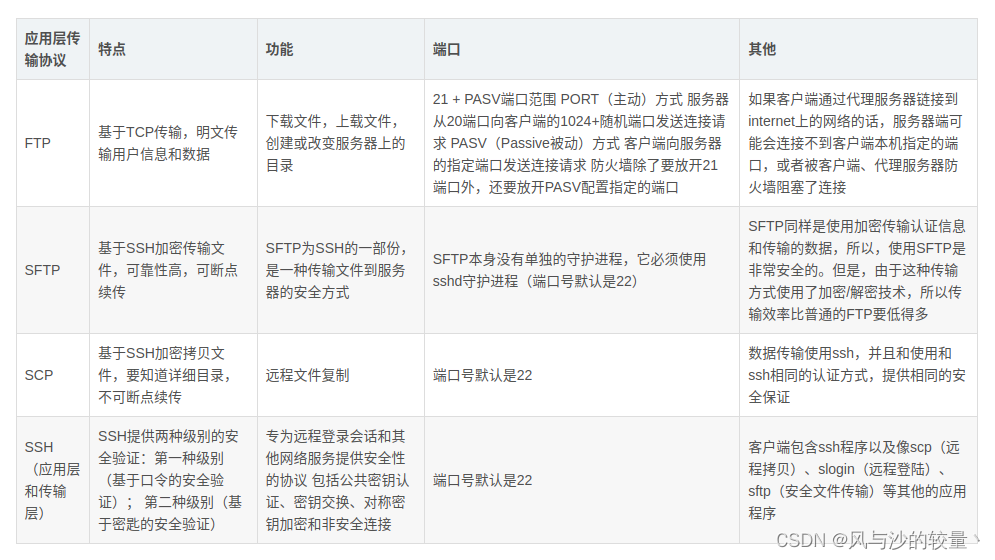
ftp和sftp区别,以及xftp的使用
网上找链接找的很辛苦对吧! 网上下载的破解版还不用。而且用没多久又说要更新了,又得重新找。 这下直接把官方免费获取链接发给你,就不用在被这种事情麻烦了。 家庭/学校免费 - NetSarang Website (xshell.com):家庭/学校免费 - NetSarang W…...
—— Hello World)
C++ 编程入门(一)—— Hello World
C 是什么环境搭建第一个 C 程序本篇结语 C 是什么 C 是一种面向对象的计算机程序设计语言,由美国 AT&T 贝尔实验室的 Bjarne Stroustrup 在 20 世纪 80 年代初期发明并实现(最初这种语言被称作 “C with Classes” 带类的 C 语言)。它是一…...
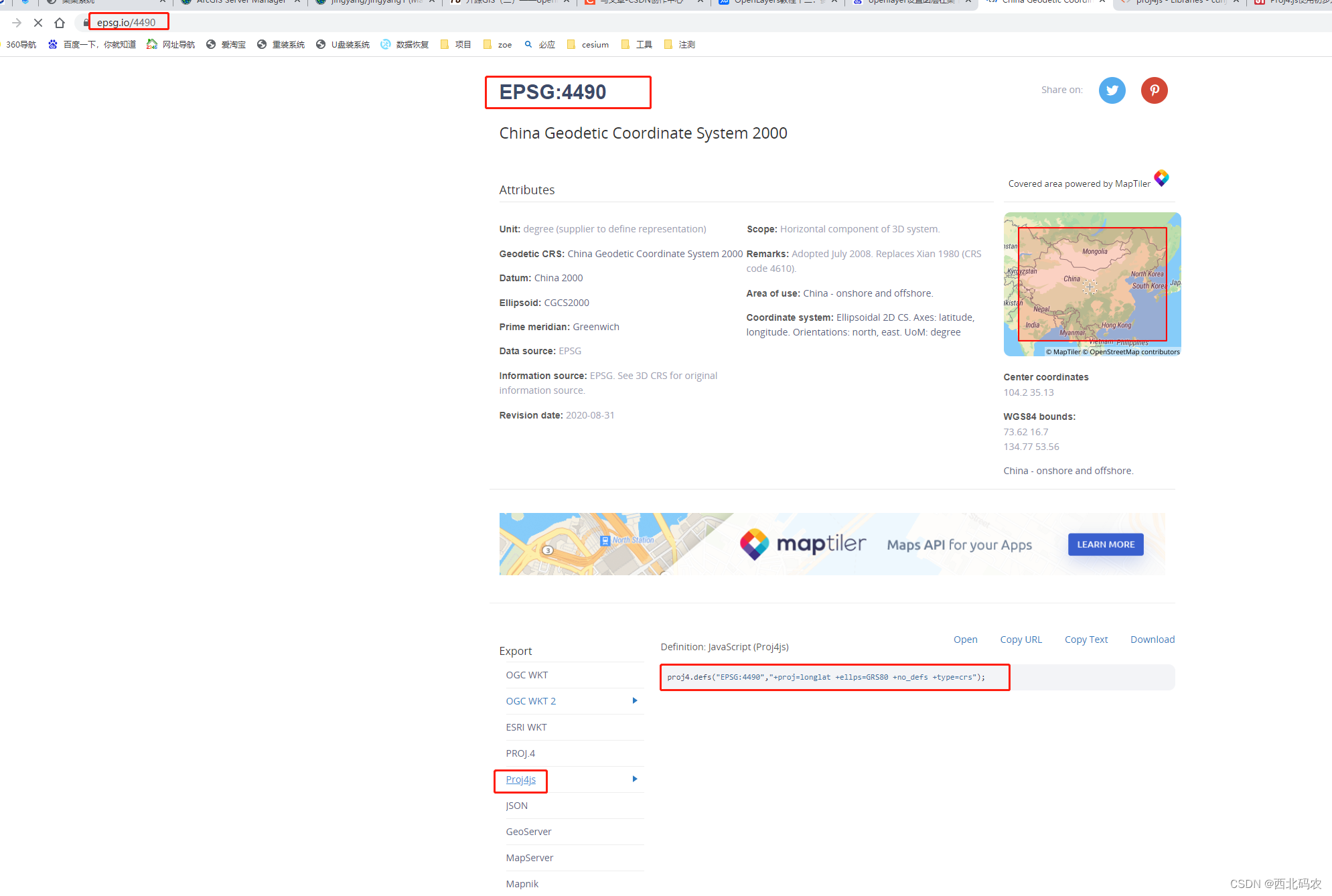
openlayers系列:加载arcgis和geoserver在线离线切片
https://www.freesion.com/article/1751396517/ 1.背景 有个项目需要使用openlayer加载各种服务上发布的数据,坐标系也不同,我们都知道openalyer默认可以加载EPAG:3857,要加载4490的坐标系的数据需要重新定义一下,之后再加载。一想起要重新…...
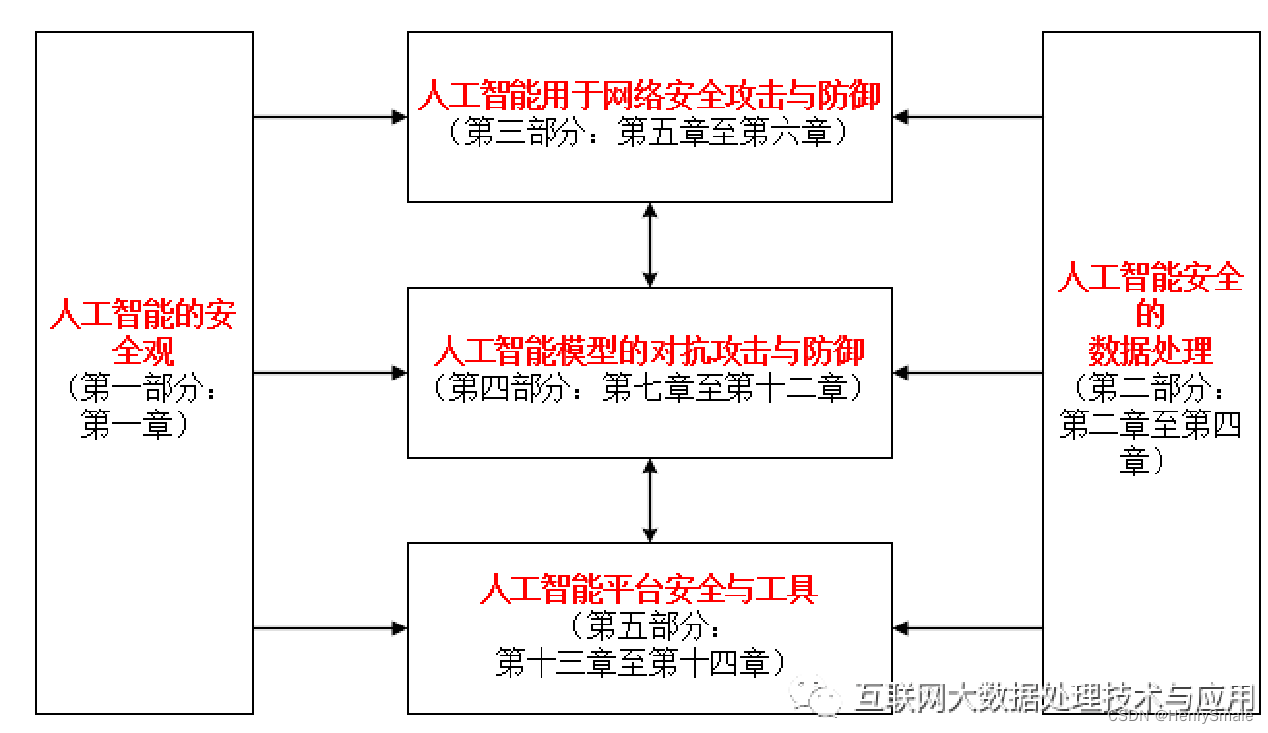
《人工智能安全》课程总体结构
1 课程内容 人工智能安全观:人工智能安全问题、安全属性、技术体系等基本问题进行了归纳整理。人工智能安全的主要数据处理方法,即非平衡数据分类、噪声数据处理和小样本学习。人工智能技术赋能网络空间安全攻击与防御:三个典型实例及攻击图…...
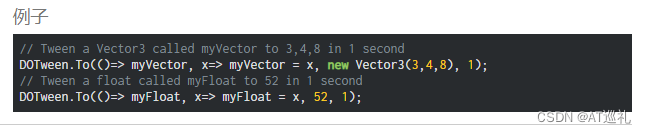
unity关于匀速移动某些值的方法
可能很多人会用到Verctor3.Lerp、Mathf.LerpUnclamped等等 这种其实不是匀速 看一下这个整体差不多的逻辑 public static float Lerp(float a, float b, float t){return a (b - a) * t;};这个逻辑就是,从a值到b值,返回一个a值加(b值-a值&…...

解决VScode下载太慢的问题记录
最近突然想重新下载vscoded便携免安装版,发现下载很慢,于是乎查询一下,以便记录 下载地址 VScode官方网站: https://code.visualstudio.com/ 根据个人的需求选择下载,页面加载下载需要等一会, 然后就会…...
Gitlab服务器备份恢复及系统升级
居安思危,思则有备,有备无患。 基于此,申请了一个测试服务器,准备先安装同版本服务器,按照最新的数据进行恢复,然后再将现在的服务器升级到Gitlab的最新版本,记录一下完整的过程,以…...

docker入门讲解
目录 第 1 章 Docker核心概念与安装 为什么使用容器? Docker是什么 Docker设计目标 Docker基本组成 容器 vs 虚拟机 Docker应用场景 Linux 安装 Docker 第 2 章 Docker镜像管理 镜像是什么 镜像从哪里来? 镜像与容器联系 镜像常用管理命令 镜像存储核心技术:联…...
))
【Matlab】基于卷积神经网络的数据回归预测(Excel可直接替换数据))
【Matlab】基于卷积神经网络的数据回归预测(Excel可直接替换数据) 1.模型原理2.数学公式3.文件结构4.Excel数据5.分块代码6.完整代码7.运行结果1.模型原理 基于卷积神经网络(Convolutional Neural Network,CNN)的数据回归预测是一种常见的机器学习方法,适用于处理具有空…...

在Springboot集成Activiti工作流引擎-引入、调用,测试【基础讲解】
工作流 通过计算机对业务流程自动化执行管理 他主要解决的是使在多个参与者之间按照某种“预定义规则”自动进行传递稳定 信息或任务的过程 通俗来讲 业务上一个玩着的审批流程 比如请假,出差 外出采购等 工作流引擎就是来解决流程问题的 提高我们的工作效率 如果…...

Java书签 #解锁MyBatis的4种批量插入方式及ID返回姿势
1. 今日书签 项目开发中,我们经常会用到单条插入和批量插入。但是实际情况可能是,项目初期由于种种原因,在业务各处直接使用单条插入SQL进行开发(未开启批处理),在后面的迭代中,系统性能问题渐…...

在react项目中如何引入国际化
react-i18next 在 React 项目中引入国际化(Internationalization,简称 i18n)可以使用第三方库来实现。其中,最常用且流行的国际化库是 react-i18next,它基于 i18next 实现,提供了方便易用的国际化功能。下…...

spring学习笔记十三
注解实现管理第三方Bean和为第三方Bean注入资源 1、添加pom坐标 <dependency><groupId>com.alibaba</groupId><artifactId>druid</artifactId><version>1.1.16</version></dependency> 2、SpringConfig配置类 Configuratio…...
react native 本地存储 AsyncStorage
An asynchronous, unencrypted, persistent, key-value storage system for React Native. Async Storage 只能用来储存字符串数据,所以为了去储存object类型的数据,得先进行序列化(JSON.stringify())当你想要使用数据的时候&…...

Postgresql数据库中的时间类型汇总
PostgreSQL数据库有以下几种时间类型 1 日期 date:表示日期,格式为YYYY-MM-DD。 2 时间 time:表示时间,格式为HH:MI:SS。 3 日期和时间 timestamp:表示日期和时间,格式为YYYY-MM-DD HH:MI:SS。 4 带…...

算法刷题Day 51 最佳买卖股票时机含冷冻期+买卖股票的最佳时期含手续费
Day 51 动态规划 309. 最佳买卖股票时机含冷冻期 关键是要画出状态转移图 然后根据状态转移图来写状态转移方程 class Solution { public:int maxProfit(vector<int>& prices) {int len prices.size();vector<vector<int>> dp(len, vector<int&g…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...
