万向节死锁
要理解万向节死锁的产生原因,首先要理解欧拉角变换,欧拉角变换是基于最初始的坐标进行变换而非变换后的坐标进行变换。
欧拉角变换需要空间中的三个角(即变换后每个轴的偏移量),另外还有每个轴的变换顺序。值得注意的是,如果按照不同轴的顺序来改变每个角,其变换的结果是不一样的。
在Unity中,变换顺序为Y>Z>X
所以先对Y轴变换,就不会影响Z和X轴
初始时物体:
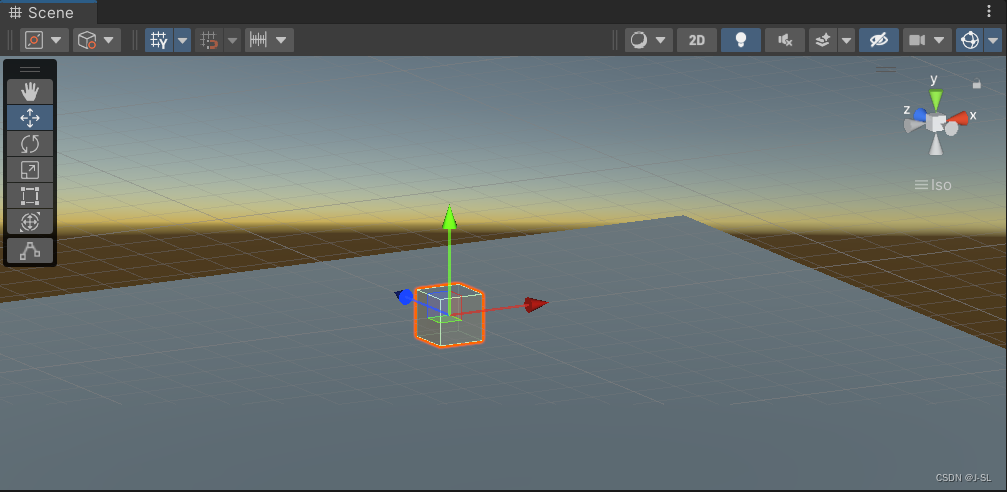
对Y轴旋转90°:
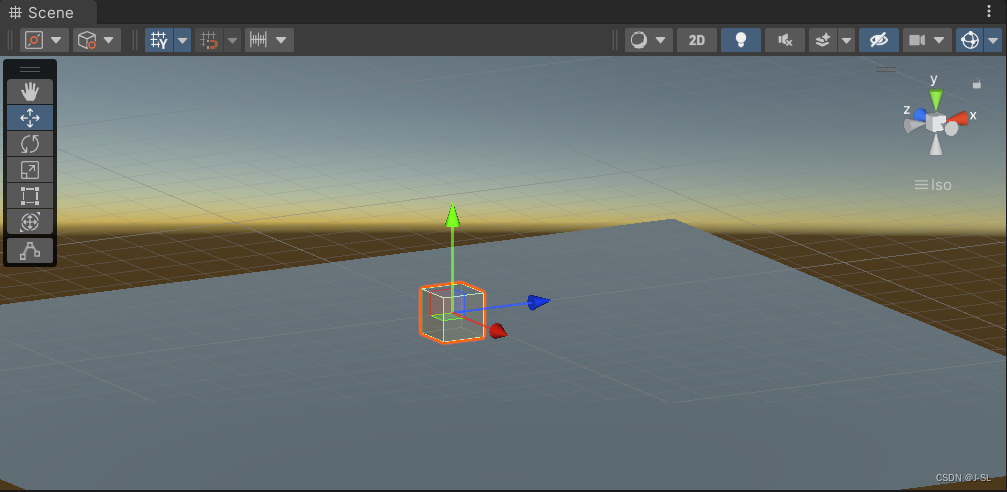
旋转X轴:正常

旋转Z轴:正常
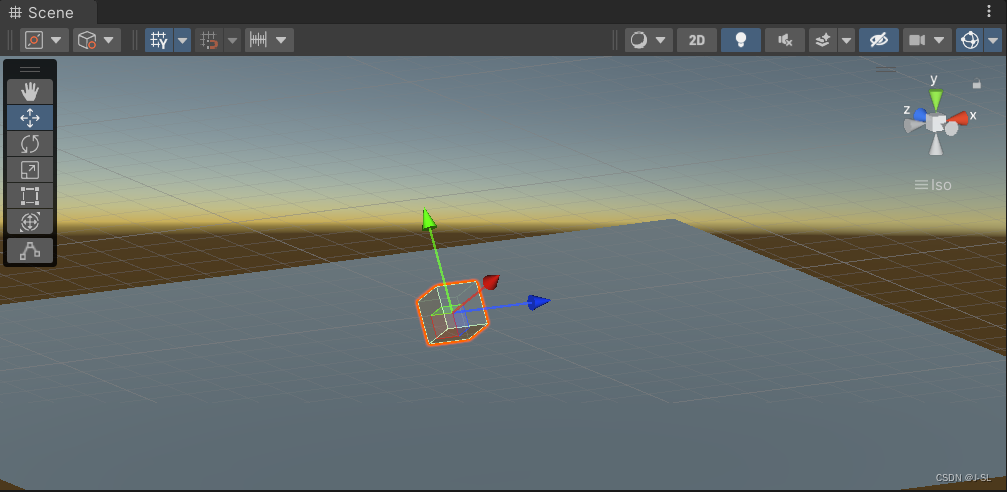
对Z轴进行变换,根据理论,由于Y轴的变换顺序高于Z轴,故Z轴先进行改变,就不符合Unity原有的变换顺序,必然在旋转轴时会发生“异常”:
先旋转Z轴90°:
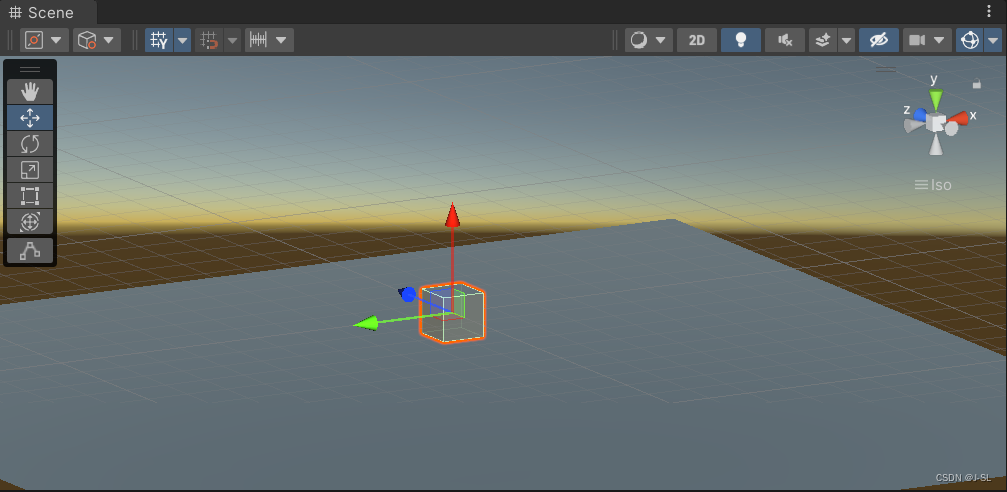
再旋转X轴:
发现物体却是绕Y轴进行旋转,但是别忘了:由于事先旋转了Z轴,导致初始坐标的X,Y轴发生了变换,而欧拉角变换却是基于初始坐标轴来变换的
旋转Z轴90°,那么相当于X,Y轴交换了,所以从人的视觉效果上看起来,转动X轴时看上去是转动Y轴(其实是转动初始坐标系的X轴)
转动Y轴:
果然,转动Y轴时,视觉看上去却是围绕X轴进行旋转。
如果先转动X轴又会发生说明情况呢:
先转动X轴90° :

转动Y轴:

看上去是绕Z轴旋转
转动Z轴:
看上去仍是绕Z轴旋转。
这便是万向节死锁,在X轴旋转至90°时,不论是操作Y/Z轴,其效果都是一样的,相当于丢失了一个自由度。
为了解决这个问题,四元数就是个很好的方法,下期我将介绍一下四元数。
相关文章:

万向节死锁
要理解万向节死锁的产生原因,首先要理解欧拉角变换,欧拉角变换是基于最初始的坐标进行变换而非变换后的坐标进行变换。 欧拉角变换需要空间中的三个角(即变换后每个轴的偏移量),另外还有每个轴的变换顺序。值得注意的…...

大数据课程D1——hadoop的初识
文章作者邮箱:yugongshiyesina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 了解大数据的概念; ⚪ 了解大数据的部门结构; ⚪ 了解hadoop的定义; ⚪ 了解hadoop的发展史; 一、大数据简介 1. 概述…...

xml命名空间
xml命名空间 一个xml文档中可以包含多个元素和属性,在文档中使用多个DTD文件时,可能会碰到相同的元素,而这些名称相同的元素可能代表了完全不同的含义,为了防止命名冲突,W3C提供了一个推荐标准-XML命名空间 命名空间有…...
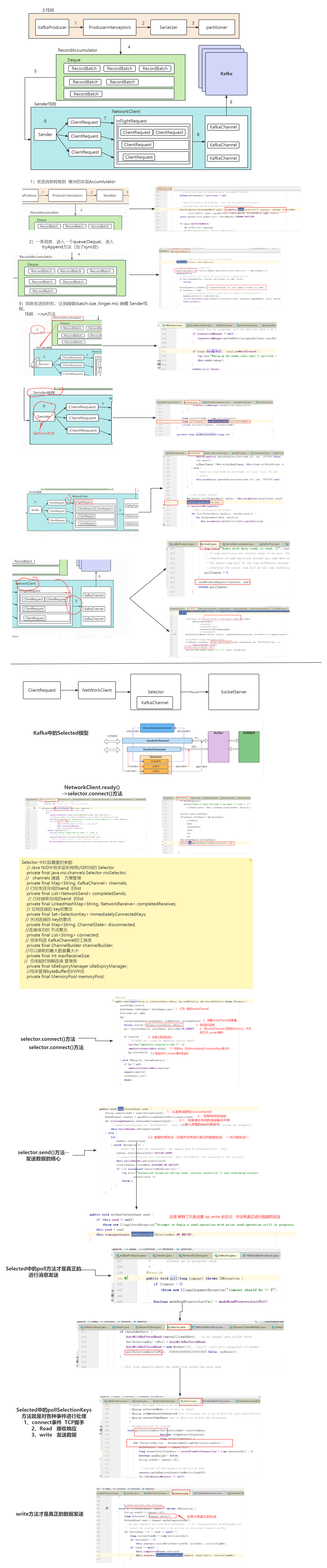
七、Kafka源码分析之网络通信
1、生产者网络设计 架构设计图 2、生产者消息缓存机制 1、RecordAccumulator 将消息缓存到RecordAccumulator收集器中, 最后判断是否要发送。这个加入消息收集器,首先得从 Deque 里找到自己的目标分区,如果没有就新建一个批量消息 Deque 加进入 2、消…...
WEB安全测试通常要考虑的测试点
1、问题:没有被验证的输入 测试方法: 数据类型(字符串,整型,实数,等) 允许的字符集 最小和最大的长度 是否允许空输入 参数是否是必须的 重复是否允许 数值范围 特定的值(枚举型&a…...
的duration音频长度获取不到问题)
关于uni.createInnerAudioContext()的duration音频长度获取不到问题
关于uni.createInnerAudioContext()的duration音频长度获取不到问题 代码如下: onLoad() {let _this this//初始化语音播放对象this.audioObj uni.createInnerAudioContext();this.audioObj.src 音频链接;// 音频进入可以播放状态,但不保证后面可以流…...

使用rknn-toolkit2把YOLOV5部署到OK3588上
使用rknn-toolkit2把YOLOV5部署到OK3588上 虚拟环境搭建软件包安装在PC机上运行yolov5目标检测 虚拟环境搭建 首先在PC的ubuntu系统安装虚拟环境: 我的服务器是ubuntu18.04版本,所以安装python3.6 conda create -n ok3588 python3.6 需要键盘输入y&…...

【雕爷学编程】Arduino动手做(93)--- 0.96寸OLED液晶屏模块14
37款传感器与执行器的提法,在网络上广泛流传,其实Arduino能够兼容的传感器模块肯定是不止这37种的。鉴于本人手头积累了一些传感器和执行器模块,依照实践出真知(一定要动手做)的理念,以学习和交流为目的&am…...
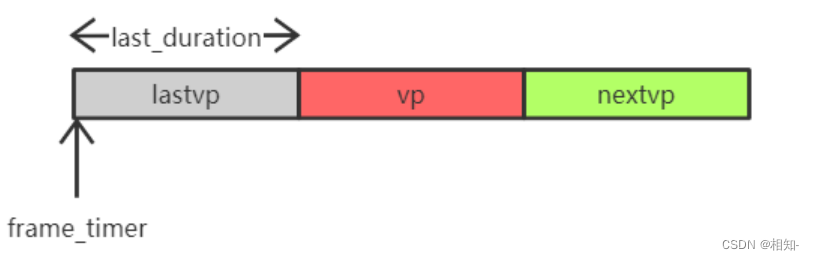
ffplay播放器剖析(5)----视频输出剖析
文章目录 1.视频输出模块1.1 视频输出初始化1.1.1 视频输出初始化主要流程1.1.2 calculate_display_rect初始化显示窗口大小 1.2 视频输出逻辑1.2.1 event_loop开始处理SDL事件1.2.2 video_refresh1.2.2.1 计算上一帧显示时长,判断是否还要继续上一帧1.2.2.2 估算当前帧显示时长…...
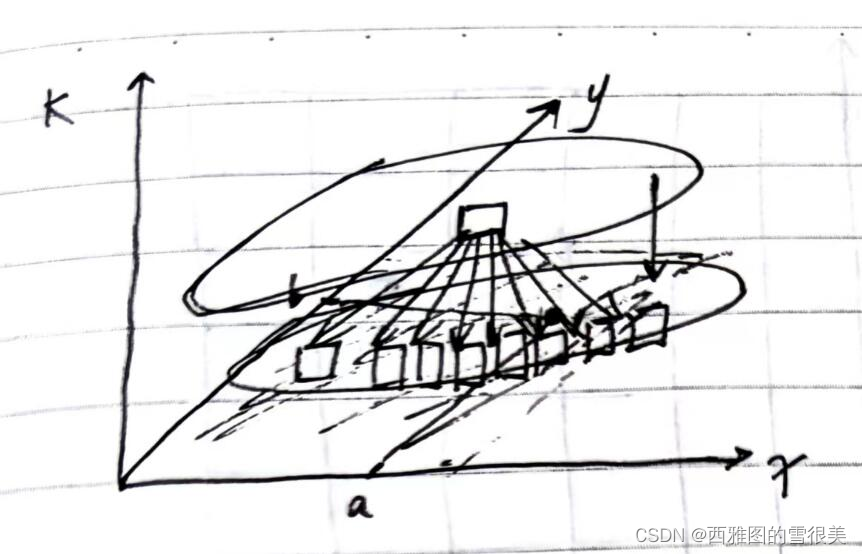
21.2:象棋走马问题
请同学们自行搜索或者想象一个象棋的棋盘, 然后把整个棋盘放入第一象限,棋盘的最左下角是(0,0)位置 那么整个棋盘就是横坐标上9条线、纵坐标上10条线的区域 给你三个 参数 x,y,k 返回“马”从(0,0)位置出发,必须走k步 …...

【CSS】手写 Tooltip 提示组件
文章目录 效果示例代码实现 效果示例 代码实现 <!DOCTYPE html> <html><head><meta charset"utf-8"><title>一颗不甘坠落的流星</title><style>body {padding: 120px;}.tooltip {position: relative;display: inline-blo…...

MySQL DDL语法
MySQL DDL语法 DDL简介 MySQL DDL(Data Definition Language)是用于定义和管理数据库结构的语言。它包括创建、修改和删除数据库、表、视图、索引和其他数据库对象的语句。DDL语法的重要性如下: 数据库结构定义:DDL语句用于创建…...

Git 绑定账号 和clone
一:环境: 下载安装完成Git,在桌面或文件夹下(在你将要保存代码的位置)右击可以看到Git Bash Here,点击可以进入黑窗口 二:配置公钥 1.查看当前状态(如果已绑定,且知道密码可以登陆,可以直接获取SSH公钥并配置即可拉取代码) git config --list 2.配置全局git用户名和邮箱 …...
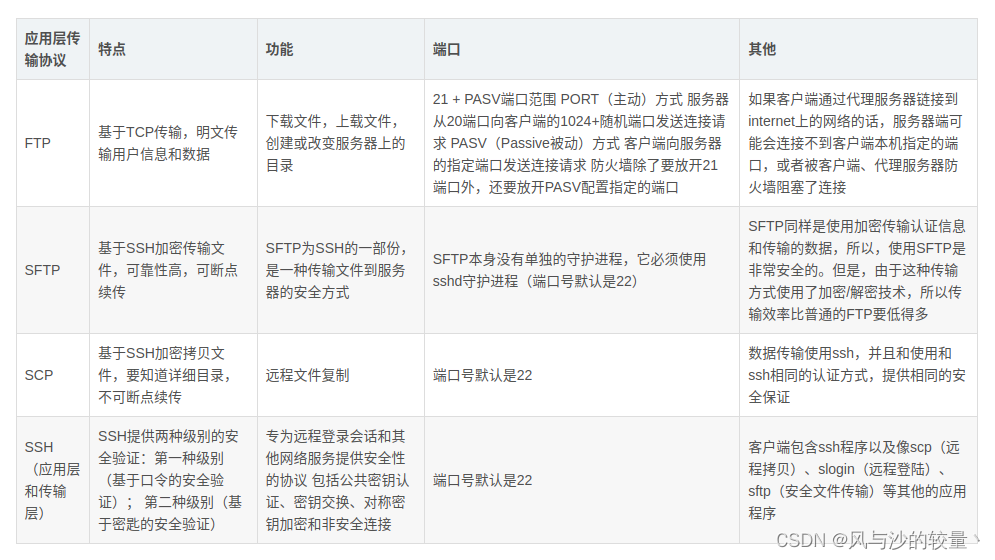
ftp和sftp区别,以及xftp的使用
网上找链接找的很辛苦对吧! 网上下载的破解版还不用。而且用没多久又说要更新了,又得重新找。 这下直接把官方免费获取链接发给你,就不用在被这种事情麻烦了。 家庭/学校免费 - NetSarang Website (xshell.com):家庭/学校免费 - NetSarang W…...
—— Hello World)
C++ 编程入门(一)—— Hello World
C 是什么环境搭建第一个 C 程序本篇结语 C 是什么 C 是一种面向对象的计算机程序设计语言,由美国 AT&T 贝尔实验室的 Bjarne Stroustrup 在 20 世纪 80 年代初期发明并实现(最初这种语言被称作 “C with Classes” 带类的 C 语言)。它是一…...
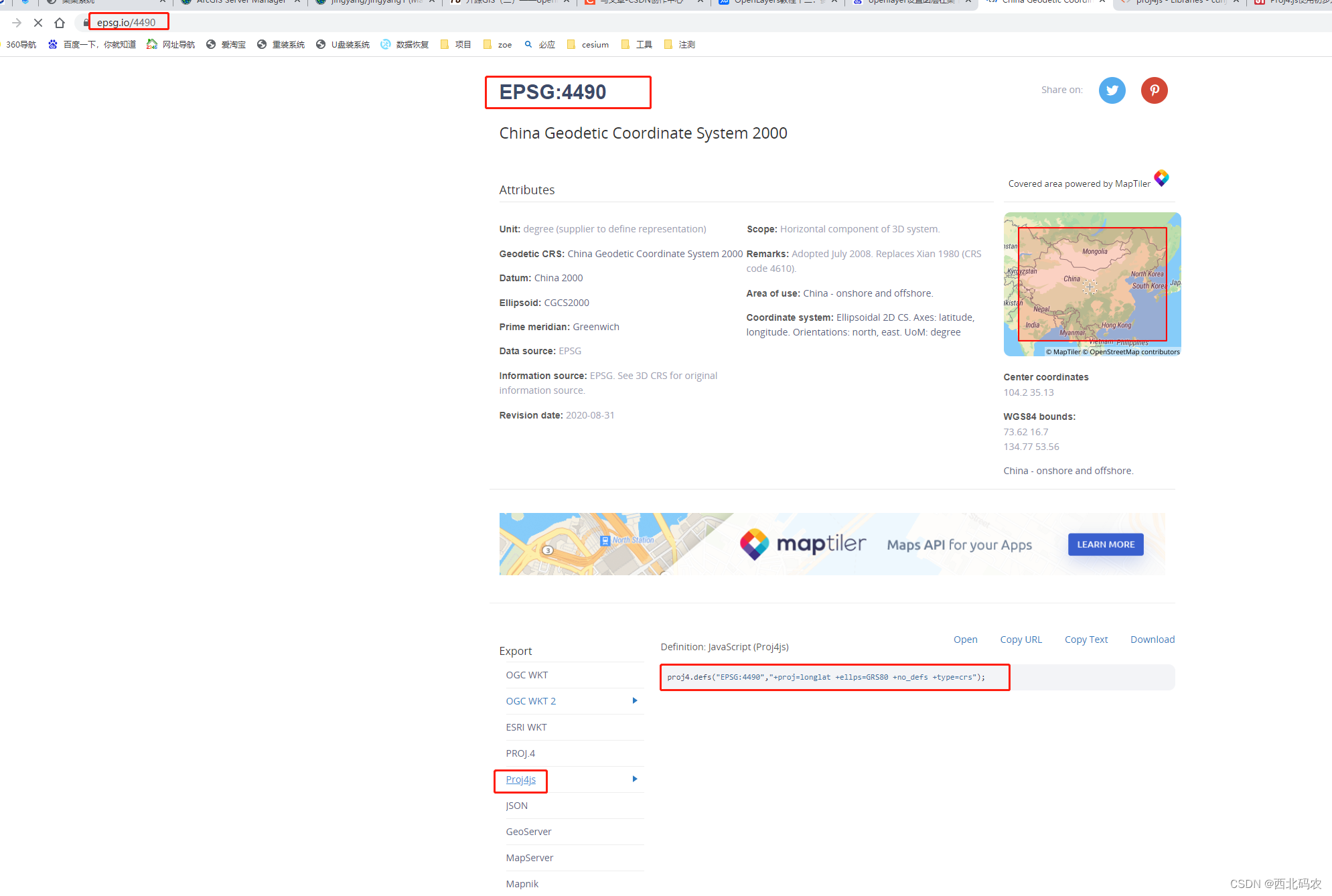
openlayers系列:加载arcgis和geoserver在线离线切片
https://www.freesion.com/article/1751396517/ 1.背景 有个项目需要使用openlayer加载各种服务上发布的数据,坐标系也不同,我们都知道openalyer默认可以加载EPAG:3857,要加载4490的坐标系的数据需要重新定义一下,之后再加载。一想起要重新…...
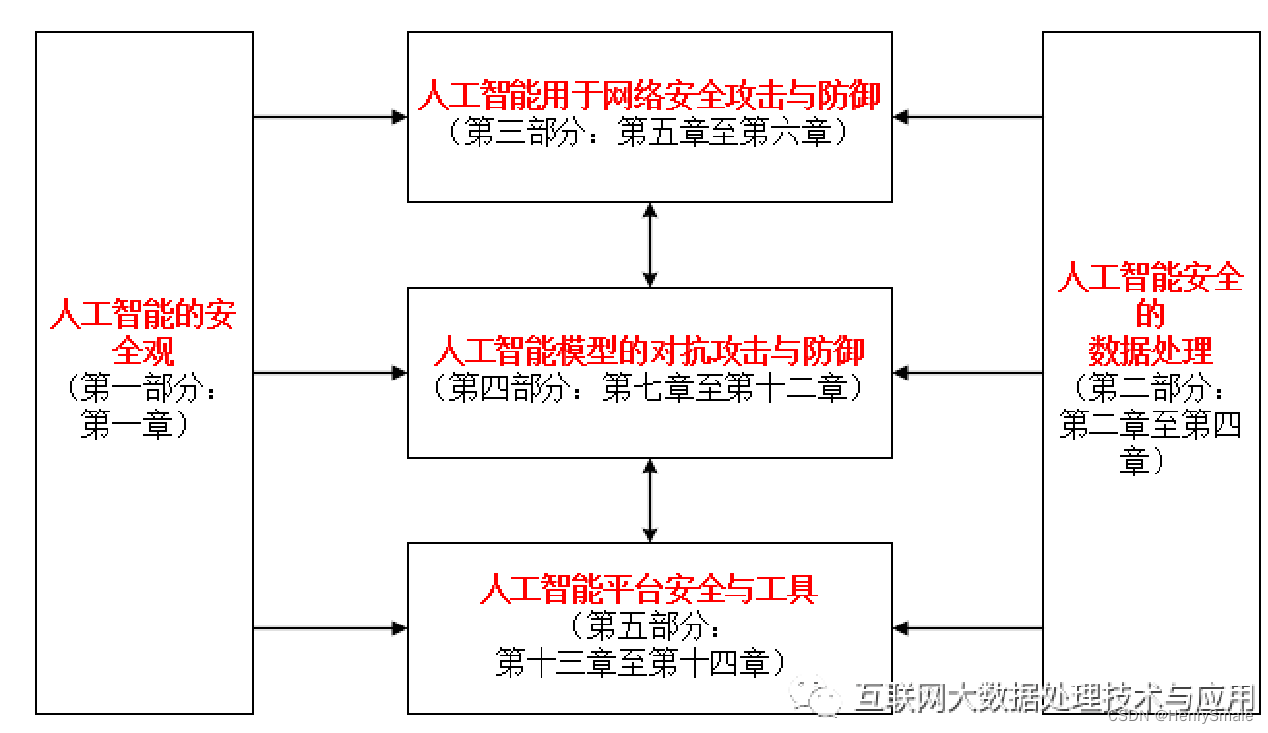
《人工智能安全》课程总体结构
1 课程内容 人工智能安全观:人工智能安全问题、安全属性、技术体系等基本问题进行了归纳整理。人工智能安全的主要数据处理方法,即非平衡数据分类、噪声数据处理和小样本学习。人工智能技术赋能网络空间安全攻击与防御:三个典型实例及攻击图…...
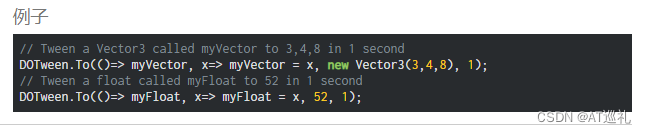
unity关于匀速移动某些值的方法
可能很多人会用到Verctor3.Lerp、Mathf.LerpUnclamped等等 这种其实不是匀速 看一下这个整体差不多的逻辑 public static float Lerp(float a, float b, float t){return a (b - a) * t;};这个逻辑就是,从a值到b值,返回一个a值加(b值-a值&…...

解决VScode下载太慢的问题记录
最近突然想重新下载vscoded便携免安装版,发现下载很慢,于是乎查询一下,以便记录 下载地址 VScode官方网站: https://code.visualstudio.com/ 根据个人的需求选择下载,页面加载下载需要等一会, 然后就会…...
Gitlab服务器备份恢复及系统升级
居安思危,思则有备,有备无患。 基于此,申请了一个测试服务器,准备先安装同版本服务器,按照最新的数据进行恢复,然后再将现在的服务器升级到Gitlab的最新版本,记录一下完整的过程,以…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...
