机器学习深度学习——随机梯度下降算法(及其优化)
在我们没有办法得到解析解的时候,我们可以用过梯度下降来进行优化,这种方法几乎可以所有深度学习模型。
关于优化的东西,我自己曾经研究过智能排班算法和优化,所以关于如何找局部最小值,以及如何跳出局部最小值的一些基本思想是有感触的,随机梯度算法和其优化学起来倒也不难。
梯度下降算法
- 梯度下降法
- 随机梯度下降法
- 随机梯度下降算法的问题
- 标准动量优化
- Nesterov动量优化
梯度下降法
梯度下降法是一个一阶最优化算法,通常称为最速下降法,是通过函数当前点对应梯度的反方向,使用规定步长距离进行迭代搜索,从而找到函数的一个局部最小值的算法,最好的情况是找到全局最小值。
随机梯度下降法
但是直接使用使用梯度下降法的话,每次更新参数都需要用到所有的样本,样本总量太大的话就会对算法速度影响很大,所以有了随机梯度下降算法。
它是对梯度下降算法的一种改进,且每次只随机取一部分样本进行优化,样本数量一般是2的整数次幂,取值范围32~256,以保证计算精度的同时提升计算速度,是优化深度学习网络中最常用的一类算法。
其在训练中,通常会使用一个固定的学习率进行训练,即:
g t = ▽ θ t − 1 f ( θ t − 1 ) ▽ θ t = − η ∗ g t 其中, g t 是第 t 步的梯度, η 是学习率 g_t=▽_{θ_{t-1}}f(θ_{t-1})\\ ▽_{θ_t}=-η*g_t\\ 其中,g_t是第t步的梯度,η是学习率 gt=▽θt−1f(θt−1)▽θt=−η∗gt其中,gt是第t步的梯度,η是学习率
随机梯度下降算法在优化时,完全依赖于当前batch数据得到的梯度,而学习率则是调整梯度影响大小的参数,通过控制学习率η的大小,一定程度上可以控制网络训练速度。
随机梯度下降算法的问题
随机梯度下降对大多数情况都很有效,但还存在缺陷:
1、很难确定合适的η,且所有的参数使用同样的学习率可能并不是很有效。这种情况可以采用变化学习率的训练方式,如控制网络在初期以大的学习率进行参数更新,后期以小的学习率进行参数更新(其实和遗传算法中的交叉变异概率似的,大家可以去了解自适应遗传算法的思想,道理都是一样的)
2、更容易收敛到局部最优解,而且当落入到局部最优解的时候,不容易跳出。(其实也和遗传算法可能遇到的问题类似,当时是和模拟退火算法结合了,解决了过早收敛问题,实质思想就是增大变异概率,变异了就很可能跳出局部最优了)
标准动量优化
动量通过模拟物体运动时的惯性来更新网络中的参数,即更新时在一定程度上会考虑之前参数更新的方向,同时利用当前batch计算得到的梯度,将两者结合起来计算出最终参数需要更新的大小和方向。
在优化时引入动量思想旨在加速学习,特别是面对小而连续且含有很多噪声的梯度。利用动量不仅增加了学习参数的稳定性,还会更快的学习到收敛的参数。
在引入动量后,网络的参数更新方式:
g t = ▽ θ t − 1 f ( θ t − 1 ) m t = μ ∗ m t − 1 + g t ▽ θ t = − η ∗ m t m t 为当前动量的累加 μ 属于动量因子,用于调整上一步动量对参数的重要程度 g_t=▽_{θ_{t-1}}f(θ_{t-1})\\ m_t=μ*m_{t-1}+g_t\\ ▽_{θ_t}=-η*m_t\\ m_t为当前动量的累加\\ μ属于动量因子,用于调整上一步动量对参数的重要程度 gt=▽θt−1f(θt−1)mt=μ∗mt−1+gt▽θt=−η∗mtmt为当前动量的累加μ属于动量因子,用于调整上一步动量对参数的重要程度
在网络更新初期,可利用上一次参数更新,此时下降方向一致,乘以较大的μ能够进行很好的加速;在网络更新后期,随着梯度逐渐趋于0,在局部最小值来回震荡的时候,利用动量使得更新幅度增大,跳出局部最优解的陷阱。
Nesterov动量优化
Nesterov项(Nesterov动量)是在梯度更新时做出的校正,以避免参数更新的太快,同时提高灵敏度。在动量中,之前累积的动量并不会影响当前的梯度,所以Nesterov的改进就是让之前的动量直接影响当前的动量,即:
g t = ▽ θ t − 1 f ( θ t − 1 − η ∗ μ ∗ m t − 1 ) m t = μ ∗ m t − 1 + g t ▽ θ t = − η ∗ m t g_t=▽_{θ_{t-1}}f(θ_{t-1}-η*μ*m_{t-1})\\ m_t=μ*m_{t-1}+g_t\\ ▽_{θ_t}=-η*m_t gt=▽θt−1f(θt−1−η∗μ∗mt−1)mt=μ∗mt−1+gt▽θt=−η∗mt
Nesterov动量与标准动量区别在于,在当前batch梯度的计算上,Nesterov动量的梯度计算是在施加当前速度之后的梯度。所以可以看成是在标准动量的方法上添加了一个校正因子,从而提高算法更新性能。
在训练开始的时候,参数可能离最最优质的较远,需要较大学习率,经过几轮训练后,减小训练学习率 (其实就是和自适应遗传算法的思想类似)。因此也提出了很多自适应学习率的算法Adadelta、RMSProp及adam等。
相关文章:
)
机器学习深度学习——随机梯度下降算法(及其优化)
在我们没有办法得到解析解的时候,我们可以用过梯度下降来进行优化,这种方法几乎可以所有深度学习模型。 关于优化的东西,我自己曾经研究过智能排班算法和优化,所以关于如何找局部最小值,以及如何跳出局部最小值的一些基…...

【MTK平台】【wpa_supplicant】关于wpa_supplicant_8/src/p2p/p2p.c文件的介绍
本文主要介绍external/wpa_supplicant_8/src/p2p/p2p.c文件 先看下p2p_find 这个方法 P2P_find 主要用于 P2P(点对点)网络中查找其他对等方的功能。另外可以看到设置P2P模块的状态为 P2P_SEARCH int p2p_find(struct p2p_data *p2p, unsigned int tim…...

华为数通HCIP-流量过滤与转发路径控制
流量控制 分类:流量过滤、流量转发路径控制; 特点:1、作用于数据层面/转发层面; 2、不会影响路由表,针对转发流量生效; 实现步骤: 1、通过流量匹配工具匹配流量(ACL…...

SpringBoot中定时任务开启多线程避免多任务堵塞
场景 SpringBoot中定时任务与异步定时任务的实现: SpringBoot中定时任务与异步定时任务的实现_霸道流氓气质的博客-CSDN博客 使用SpringBoot原生方式实现定时任务,已经开启多线程支持,以上是方式之一。 除此之外还可通过如下方式。 为什…...
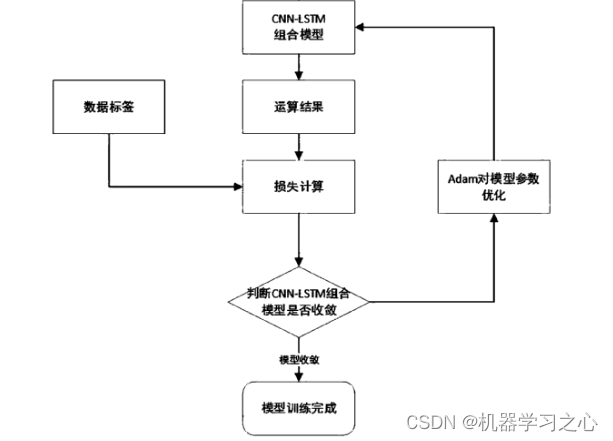
回归预测 | MATLAB实现SO-CNN-BiLSTM蛇群算法优化卷积双向长短期记忆神经网络多输入单输出回归预测
回归预测 | MATLAB实现SO-CNN-BiLSTM蛇群算法优化卷积双向长短期记忆神经网络多输入单输出回归预测 目录 回归预测 | MATLAB实现SO-CNN-BiLSTM蛇群算法优化卷积双向长短期记忆神经网络多输入单输出回归预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 Matlab实…...
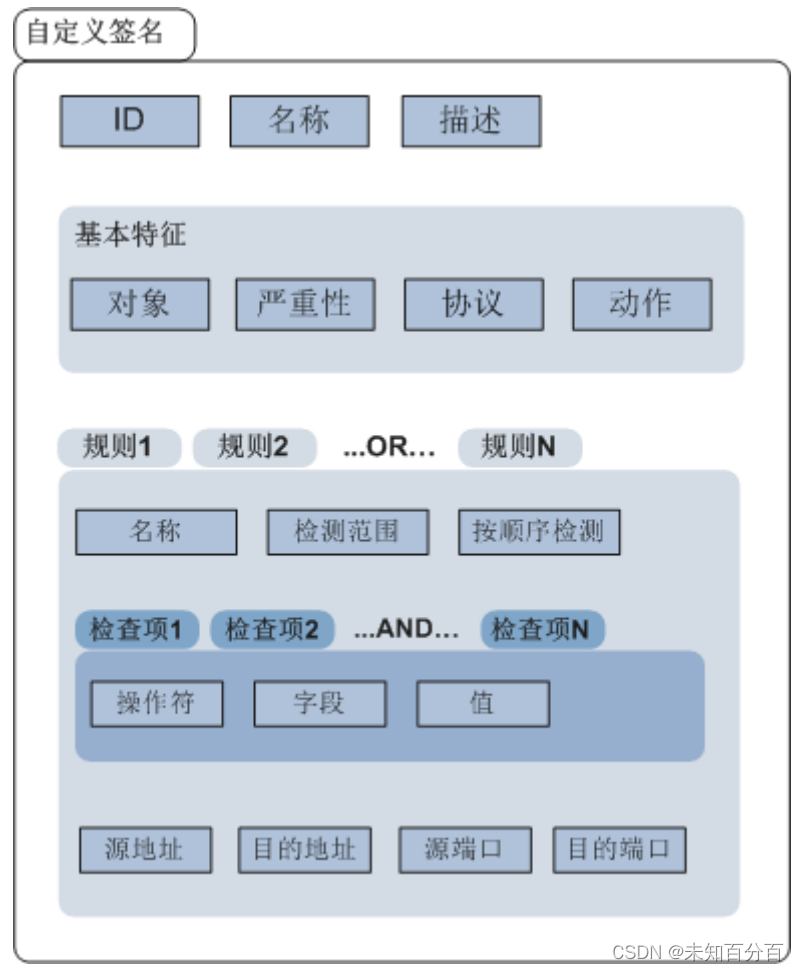
入侵检测——IDS概述、签名技术
1. 什么是IDS? IDS(intrusion detection system)入侵检测系统,是一种对网络传输进行即时监视,在发现可疑传输时发出警报或者采取主动反应措施的网络安全设备。它会对系统的运行状态进行监视,发现各种攻击企…...

golang 标准库json Marshal 序列化与反序列化
标准库代码 func Marshal(v any) ([]byte, error) {e : newEncodeState()defer encodeStatePool.Put(e)err : e.marshal(v, encOpts{escapeHTML: true})if err ! nil {return nil, err}buf : append([]byte(nil), e.Bytes()...)return buf, nil }func Unmarshal(data []byte, …...
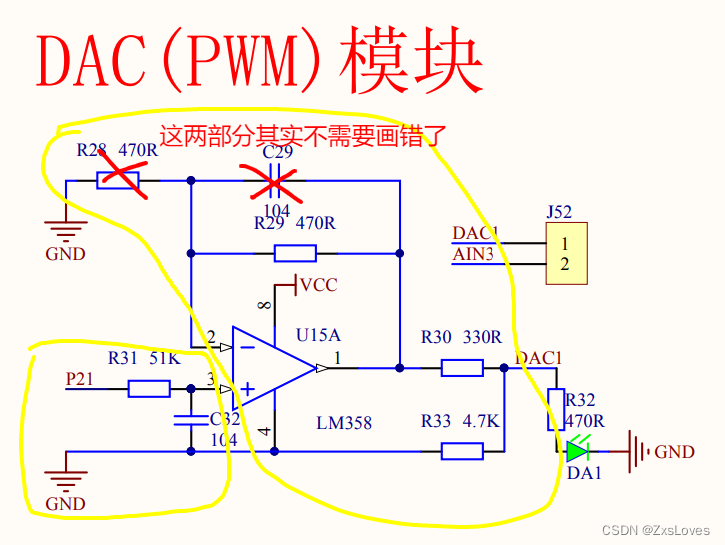
【【51单片机AD/DA的分析】】
51单片机AD/DA的分析 看似单片机实验,其实是要学好数电 模数转换 与 数模转换 运算放大器 DA的转换就是利用运算放大器实现的 输出电压v0-(D7~D0)/256 x (VrefxRfb)/R D7~D0 就是我们控制的按键看输入多少 然后再划分256份 Vref是我们设置的一个基准电压 PWM 这种…...
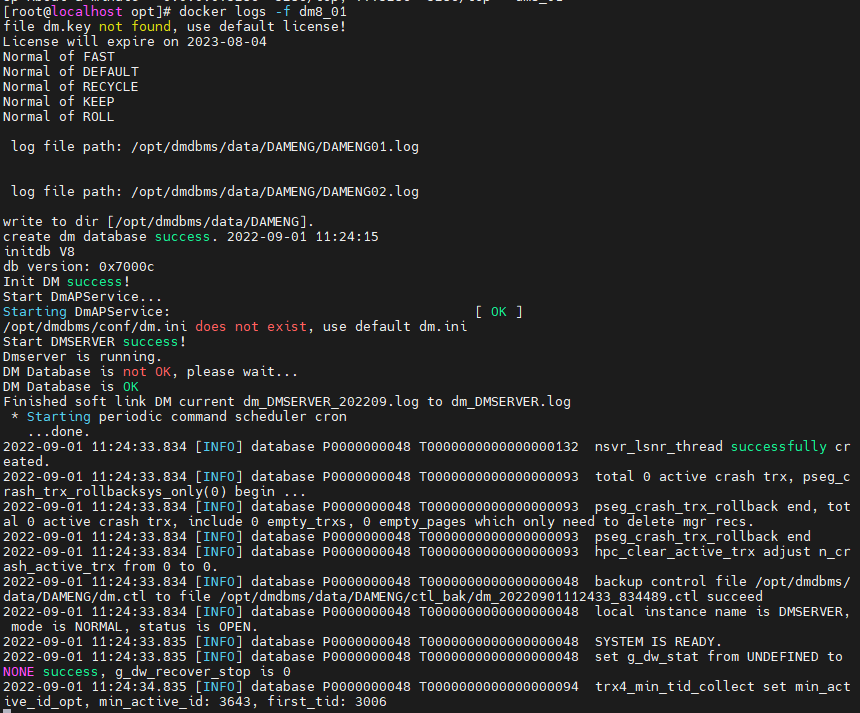
在docker中安装使用达梦数据库
关于在docker中安装达梦数据库,达梦官方网站其实是有提供安装使用方法的,但可能还是有朋友不会,这里将在原文基础上简单扩充下。 注意:docker容器中,数据库安装后没有创建服务的脚本,只有bin、bin2、conf、…...

Leetcode-每日一题【剑指 Offer II 010. 和为 k 的子数组】
题目 给定一个整数数组和一个整数 k ,请找到该数组中和为 k 的连续子数组的个数。 示例 1: 输入:nums [1,1,1], k 2输出: 2解释: 此题 [1,1] 与 [1,1] 为两种不同的情况 示例 2: 输入:nums [1,2,3], k 3输出: 2 提示: 1 < nums.leng…...

【JavaScript】使用Promise来处理异步调用,方法传入参数为接口,并回调接口的方法
例如我们在下面这个方法传入一个接口,并将方法的执行过程用传入的接口进行回调 connect() {wx.connectSocket({url: this.url,success: () > {console.log(WebSocket 连接创建成功);},fail: (err) > {console.error(WebSocket 连接创建失败, err);}});wx.onS…...
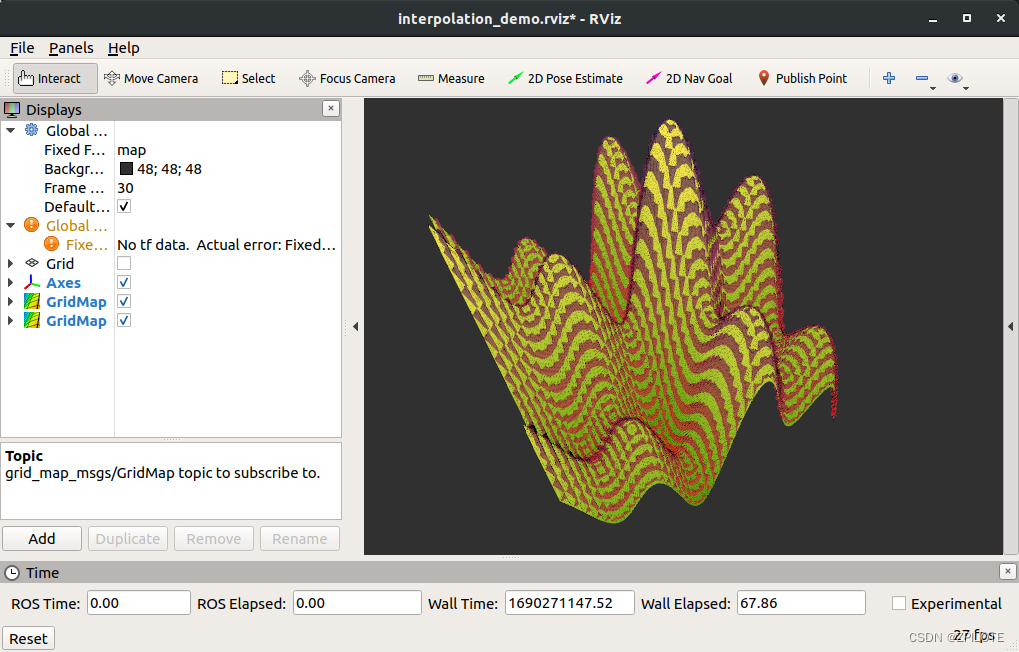
grid map学习笔记1之Ubuntu18.04+ROS-melodic编译安装grid_map栅格地图及示例运行
文章目录 0 引言1 安装依赖和编译1.1 安装依赖1.2 下载编译 2 运行示例2.1 simple_demo2.2 tutorial_demo2.3 iterators_demo2.4 image_to_gridmap_demo2.5 grid_map_to_image_demo2.6 opencv_demo2.7 resolution_change_demo2.8 filters_demo2.9 interpolation_demo 0 引言 苏…...

postgres wal2json插件jsonb字段数据丢失问题解决
使用pgwal2jsondebezium进行数据同步时,发现偶尔会有jsonb字段数据丢失的问题 进行测试时发现: 1、发生数据丢失的jsonb字段长度都比较大(超过toast阈值,使用toast表存储) 2、针对发生jsonb字段丢失的数据,jsonb字段本身未发生修…...
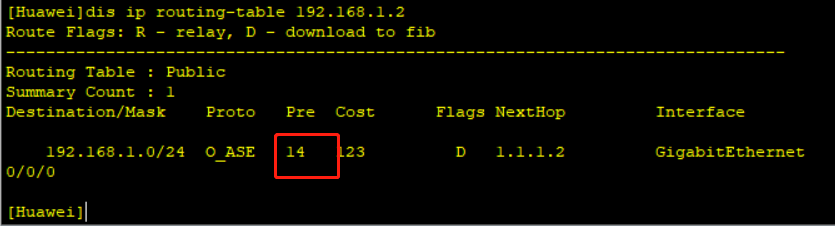
华为eNSP:路由引入
一、拓扑图 二、路由器的配置 1、配置路由器的IP AR1: [Huawei]int g0/0/0 [Huawei-GigabitEthernet0/0/0]ip add 1.1.1.1 24 [Huawei-GigabitEthernet0/0/0]qu AR2: [Huawei]int g0/0/0 [Huawei-GigabitEthernet0/0/0]ip add 1.1.1.2 24 [Huaw…...
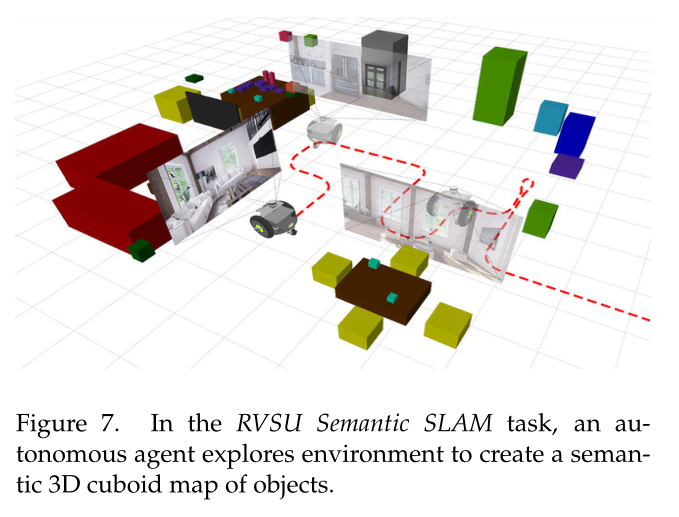
Retrospectives on the Embodied AI Workshop(嵌入式人工智能研讨会回顾) 论文阅读
论文信息 题目:Retrospectives on the Embodied AI Workshop 作者:Matt Deitke, Dhruv Batra, Yonatan Bisk 来源:arXiv 论文地址:https://arxiv.org/pdf/2210.06849 Abstract 我们的分析重点关注 CVPR Embodied AI Workshop 上…...

「JVM」Full GC和Minor GC、Major GC
Full GC和Minor GC、Major GC 一、Full GC1、什么是Full GC?2、什么情况下会触发full gc? 二、Minor GC1、什么是Minor GC?2、什么情况下会触发Minor GC? 三、Major GC1、什么是Major GC?2、什么情况下会触发Major GC?…...

Asp.Net MVC 使用Log4Net
Asp.Net MVC 使用Log4Net 在 ASP.NET MVC 中使用 Log4net 需要进行一些配置和代码集成。下面是在 ASP.NET MVC 中使用 Log4net 的步骤: 1. 安装 Log4net NuGet 包 打开 NuGet 包管理器控制台,并运行以下命令来安装 Log4net: Install-Pack…...
 | 手机平板电脑断电通知)
[元带你学: eMMC协议 29] eMMC 断电通知(PON) | 手机平板电脑断电通知
依JEDEC eMMC及经验辛苦整理,原创保护,禁止转载。 专栏 《元带你学:eMMC协议》 内容摘要 全文 2000 字, 主要内容 前言 断电通知是什么? 断电通知过程...

vue使用recorder-core.js实现录音功能
下载组件 npm install recorder-core封装方法 record.ts //必须引入的核心 import Recorder from recorder-core;//引入mp3格式支持文件;如果需要多个格式支持,把这些格式的编码引擎js文件放到后面统统引入进来即可 import recorder-core/src/engine/…...
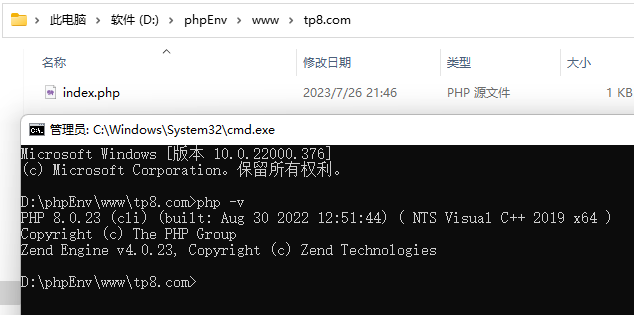
ThinkPHP8知识详解:给PHP8和MySQL8添加到环境变量
在PHPenv安装的时候,环境变量默认的PHP版本是7.4的,MySQL的版本是5.7的,要想使用ThinkPHP8来开发,就必须修改环境变量,本文就详细讲解了如果修改PHP和MySQL的环境变量。 1、添加网站 启动phpenv,网站&…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...
