图论算法:Floyd算法
文章目录
- Floyd算法
- 例题:灾后重建
Floyd算法
Floyd算法用于求图中任意两点之间的最短路径,该算法主要运用了动态规划的思想。
思考: 给你几个点与边,可以组成一张图,那么如何求得任意两点之间的最短路径呢?
我们貌似可以使用dfs或者bfs来做,那么这样做的话,我们的dfs用来求一个点到一个点之间的最短路径是可行的,但是如果是n个点?我们难道需要进行n次的dfs或者bfs吗,每次记录一个点到任意一点的最短路径,这显然是不可能的。
现在思考一个问题,假设我们的图中的每两个顶点之间的边是单向边
-
如果我们不能使用中转点:我们 1 -> 2 :那么我们就需要 找到 1->2直接的一条相连的路径,这条路径长度为e[1] [2]
-
如果我们只能使用一个中转点:我们从 1 -> 2:那么我们就需要找到 1->3 ->2(我们假设这是一个比前面 1->2路程短的路径),那么我们就可以得到: e[1] [3] + e[3] [2] 的最短路径长度
-
如果我们只能使用两个中转点:我们从 1 -> 2:那么我们就需要找到 1->3->4 ->2(我们假设这是一个比前面 1->3->2路程短的路径),那么我们就可以得到: 首先中转3:e[1] [3]+e[3] [4],然后中转4:e[1] [4] + e[4] [2] 的最短路径长度,最后的路径就是e[1] [4] + e[4] [2]
-
同理如果我们可以使用 k 个中转点。则我们便可以得到最后的最短路径就是 e[1] [k] + e[k] [2],其中 e[1] [k] 包含之前所有 k -1 个中转点的计算后的最短路径。
那么我们便可以得到一个结论:我们可以枚举 从 i 到 j 经过的前k个中转点,使得i到j的路径最短。
因此 Floyd算法的核心就是从i号顶点到j号顶点只经过前k号点的最短路程
注意:作为中转不是经过第 k 个点,而是经过了 前k 个,包含 1,2,3,4,5,6 k-1 k,即表示这 从 i到j我们可以经过总共 k 个中转点,来使得这条路径最短
算法如下:
for (int k=1;k<=n;k++)
{for (int i=1;i<=n;i++){for (int j=1;j<=n;j++){dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]);}}
}
例题:灾后重建
B 地区在地震过后,所有村庄都造成了一定的损毁,而这场地震却没对公路造成什么影响。但是在村庄重建好之前,所有与未重建完成的村庄的公路均无法通车。换句话说,只有连接着两个重建完成的村庄的公路才能通车,只能到达重建完成的村庄。
给出 B 地区的村庄数 NNN,村庄编号从 000 到 N−1N-1N−1,和所有 MMM 条公路的长度,公路是双向的。并给出第 iii 个村庄重建完成的时间 tit_iti,你可以认为是同时开始重建并在第 tit_iti 天重建完成,并且在当天即可通车。若 tit_iti 为 000 则说明地震未对此地区造成损坏,一开始就可以通车。之后有 QQQ 个询问 (x,y,t)(x,y,t)(x,y,t),对于每个询问你要回答在第 ttt 天,从村庄 xxx 到村庄 yyy 的最短路径长度为多少。如果无法找到从 xxx 村庄到 yyy 村庄的路径,经过若干个已重建完成的村庄,或者村庄 xxx 或村庄 yyy 在第 ttt 天仍未重建完成,则需要返回 -1。
这道题目就是Floyd算法的模板题。
这道题目让我们求得两个村庄之间的最短路程,因此我们就可以把两个村庄看作两个点,并且中转k个点,来求得最短路径
但是如果我们采用每次询问都 进行一次floyd算法的话查找两个点的最短路径,显然是会超时的。
我们注意到有个时间的概念在里面,即每个村庄的 修复时间 是固定的,并且是会影响到我们的选择的,因为如果我们计算 1 到 3的村庄的最短路径,可能这两个村庄的修复时间在我们所给的时间内,但是如果我们选择中转,则其他的点的时间都大于我们所给的时间,所以我们不能从其他点中转过来,但是确实从其他点中转使得 1到 3 的路程会更短,因此这个时间我们便可以设置为 k 的值,即在 k时间内中转,不能超过 k时间,因此我们就可以每次询问使用一次floyd算法了,但是我们的k是固定的,我们只需要两重循环就好了。
dp[i] [j] :表示从 i 到 j 的最短距离
状态转移方程:
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]) dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])
需要注意的几点:
- dp存储最小值,因此我们首先要初始化为 INF一个极大值
- dp[i] [i] ,即 第 i个点与第i个点之间的距离为0
- 注意 边是双向边,因此需要存储 i 到 j ,j 到 i 的距离都为边的距离
AC code
//TODO: Write code here
int n,m,q;
const int N=1e3+10;
int nums[N],dp[N][N];
void Floyd(int k)
{for (int i=0;i<n;i++){for (int j=0;j<n;j++){dp[i][j]=dp[j][i]=min(dp[i][j],dp[i][k]+dp[k][j]);}}
}
signed main()
{cin>>n>>m;for (int i=0;i<n;i++) cin>>nums[i];for (int i=0;i<n;i++){for (int j=0;j<n;j++){dp[i][j]=INF;}}for (int i=0;i<n;i++){dp[i][i]=0;}for (int i=1;i<=m;i++){int a,b,s;cin>>a>>b>>s;dp[a][b]=dp[b][a]=s; //两点之间的距离}cin>>q;int now=0;for (int i=1;i<=q;i++){int s1,s2,s3;cin>>s1>>s2>>s3;//根据时间进行处理//时间是逐渐增长的,因此每次 floyd的 k 都是随时间变化的while (nums[now]<=s3 && now<n)//目前更新的点在询问点之前{Floyd(now);//前now个时间之前更新最短路now++;}if (nums[s1]>s3 || nums[s2]>s3){cout<<-1<<endl;}else {if (dp[s1][s2]==INF) cout<<-1<<endl;else cout<<dp[s1][s2]<<endl;}}
#define one 1 return 0;
}
相关文章:

图论算法:Floyd算法
文章目录Floyd算法例题:灾后重建Floyd算法 Floyd算法用于求图中任意两点之间的最短路径,该算法主要运用了动态规划的思想。 思考: 给你几个点与边,可以组成一张图,那么如何求得任意两点之间的最短路径呢?…...

回顾 | .NET MAUI 跨平台应用开发 - 用 .NET MAUI 开发一个无人机应用(下)
点击蓝字关注我们编辑:Alan Wang排版:Rani Sun微软 Reactor 为帮助广开发者,技术爱好者,更好的学习 .NET Core, C#, Python,数据科学,机器学习,AI,区块链, IoT 等技术,将…...
部署有多个仓库的svn服务
centos7自带svn服务,现需要创建多个仓库,并实现用户读写功能 创建svn版本库 mkdir /home/svn mkdir /home/svn/confmkdir /home/svn/yk1 mkdir /home/svn/yk2 svnadmin create /home/svn/yk1 svnadmin create /home/svn/yk2 进入版本库yk1的配置文件路…...
Mapper文件注入问题
Mapper文件注入问题UserMapper that could not be found.原因分析解决方案程序正常运行,但是注入类爆红问题原因分析解决方法UserMapper’ that could not be found. 原因分析 撰写了mapper文件,但是没有注入spring容器 解决方案 添加mybatis.mapper-…...
基于微信小程序的国产动漫论坛小程序
文末联系获取源码 开发语言:Java 框架:ssm JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7/8.0 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven3.3.9 浏览器…...
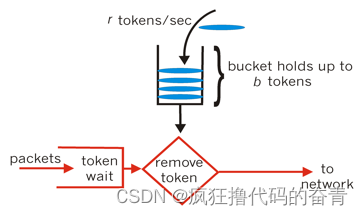
常用限流算法
简单时间窗口 算法逻辑:设置周期时间内的最大并发量问题:在周期尾端进去阈值并发后,进入下一周期时,又进入阈值并发量,则会出现瞬时并发量是阈值的2倍。 滑动时间窗口(优化) 算法逻辑…...

前端面经详解
目录 css 盒子充满屏幕 A.给div设置定位 B.设置html,body的宽高 C.相对当前屏幕高度(强烈推荐) 三列布局:左右固定,中间自适应 flex布局(强烈推荐) grid布局 magin负值法 自身浮动 绝对定位 圣…...
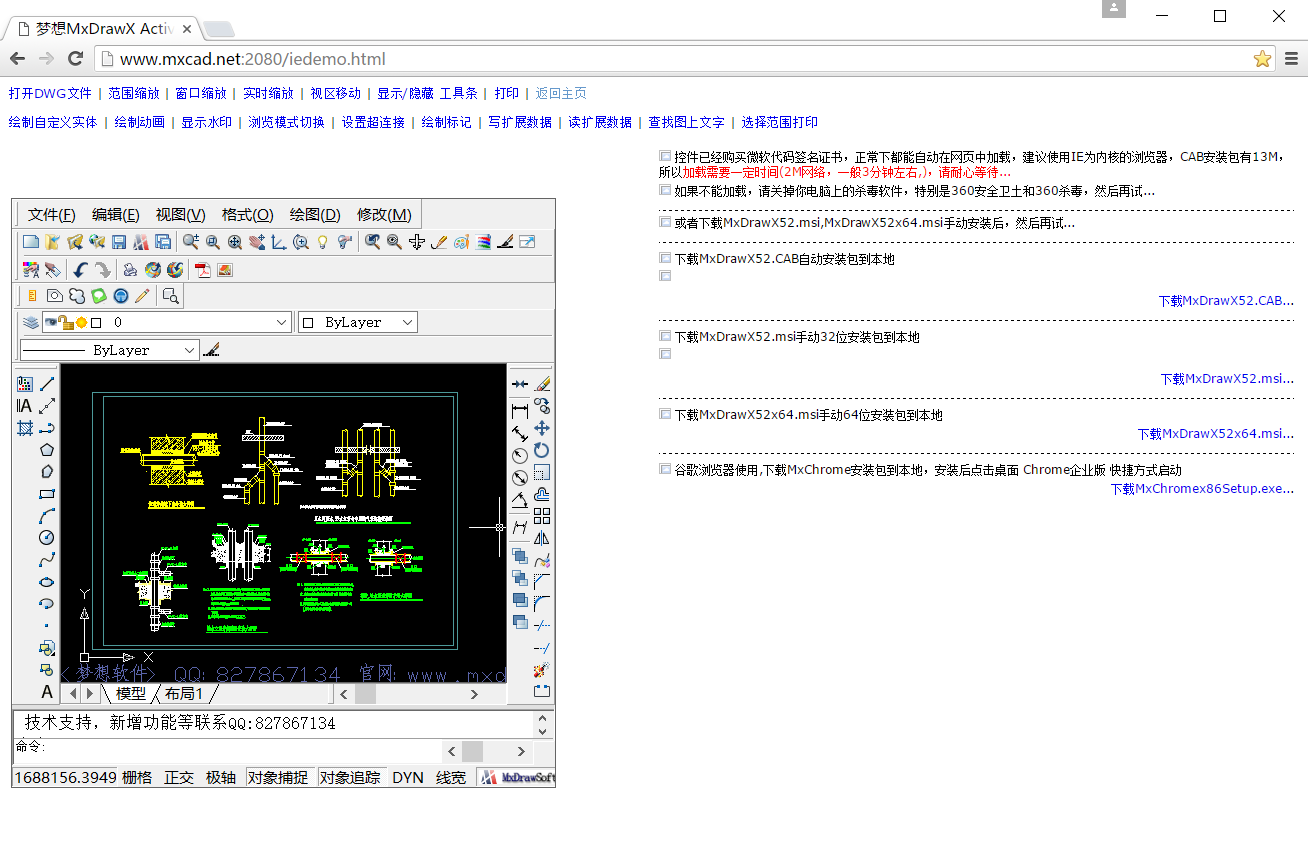
网页CAD开发快速入门
演示说明 提示:目前提供两种在网页中浏览编辑CAD图纸方案,详细说明见:MxDraw帮助 网页中打开CAD最简步骤: 第一步: 安装插件运行环境,下载安装(可能需要退杀毒软件):https://demo.mxdraw3d.com:3562/MxDrawx86Setup…...

C#开发的OpenRA的mod.yaml文件
C#开发的OpenRA的mod.yaml文件 在OpenRA游戏里,会看到这样一段代码: Manifest LoadMod(string id, string path){IReadOnlyPackage package = null;try{if (!Directory.Exists(path)){Log.Write("debug", path + " is not a valid mod package");return …...
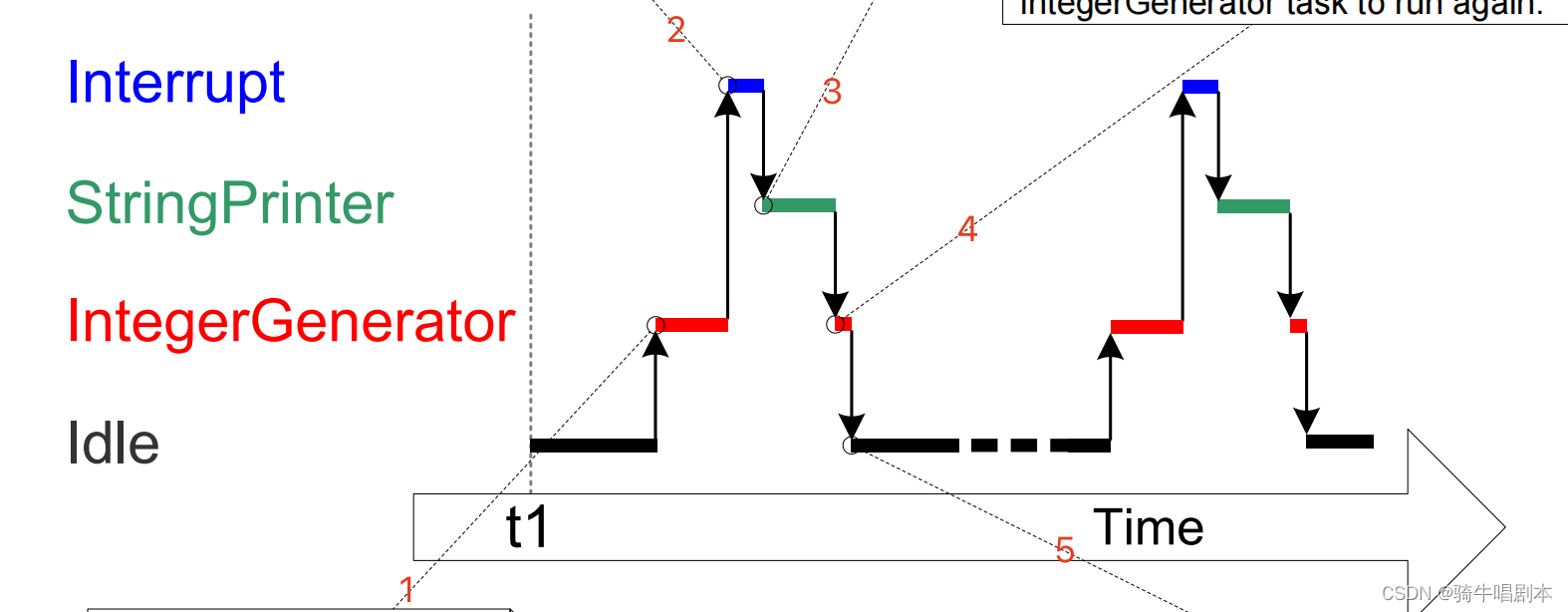
【ESP32+freeRTOS学习笔记-(七)中断管理】
目录1、概述2、在ISR中使用FreeRTOS中专用的API2.1 独立的用于ISR中的API2.2 关于xHigherPriorityTaskWoken 参数的初步理解3、延迟中断处理的方法-将中断中的处理推迟到任务中去4 方法一:用二进制信号量来同步ISR与”延时处理的任务“4.1 二进制信号量4.2 函数用法…...

【总结】1591- 从入门到精通:使用 TypeScript 开发超强的 CLI 工具
作为一名开发者,掌握 CLI 工具的开发能力是非常重要的。本文将指导你如何使用 TypeScript 和 CAC 库开发出功能强大的 CLI 工具。快速入门首先,需要先安装 Node.js 和 npm(Node Package Manager),然后在项目目录中创建…...

【Java】int和Integer的区别?为什么有包装类?
int和Integer的区别?为什么有包装类? java是一种强类型的语言,所以所有的属性都必须要有一个数据类型。 PS:java10有了局部变量类型推导,可以使用var来代替某个具体的数据类型,但是在字节码阶段࿰…...
)
【LeetCode】石子游戏 IV [H](动态规划)
1510. 石子游戏 IV - 力扣(LeetCode) 一、题目 Alice 和 Bob 两个人轮流玩一个游戏,Alice 先手。 一开始,有 n 个石子堆在一起。每个人轮流操作,正在操作的玩家可以从石子堆里拿走 任意 非零 平方数 个石子。 如果石…...
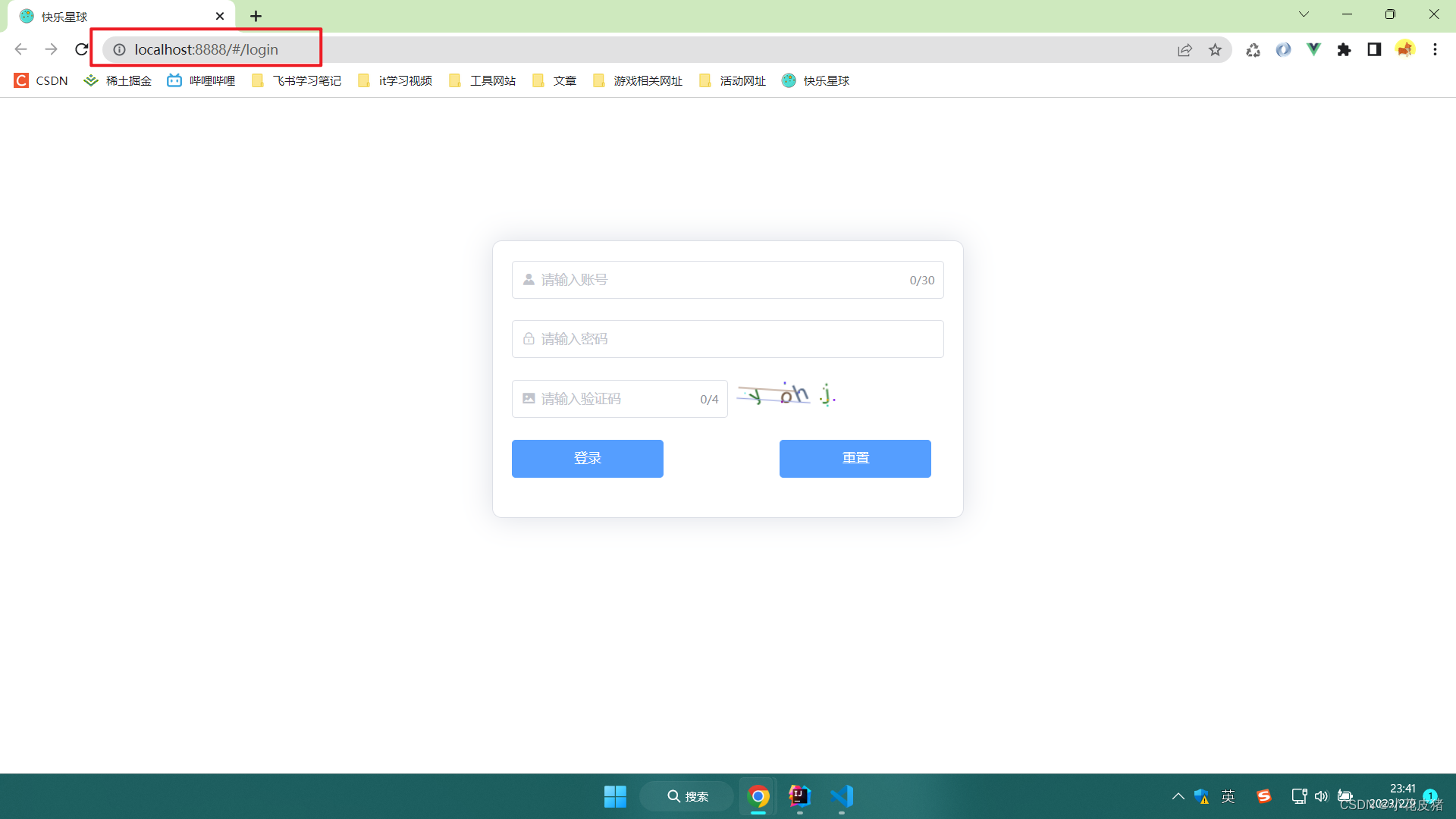
修改Vue项目运行的IP和端口
前言 我们在使用VsCode启动Vue项目的时候,我发现:默认的端口号好像和tomcat一样,默认都是8080,如果8080被占用了,就会使用8081,8082这样的方式以此类推。 那么,我们是否可以像后端一样,通过修改…...
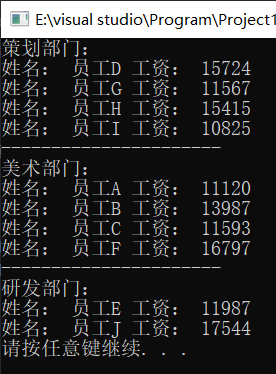
【C++提高编程】map/ multimap 容器详解(附测试用例与结果图)
目录1. map/ multimap容器1.1 map基本概念1.2 map构造和赋值1.3 map大小和交换1.4 map插入和删除1.5 map查找和统计1.6 map容器排序1.7 案例-员工分组1.7.1 案例描述1.7.2 实现步骤1. map/ multimap容器 1.1 map基本概念 简介: map中所有元素都是pairpair中第一个…...

laravel操作redis和缓存操作
一:操作redis1:redis拓展安装composer require predis/predis或者你也可以通过 PECL 安装 PhpRedis PHP 扩展,安装方法比较复杂,个人不推荐2:配置redis在config/database.php文件中配置redis(1):单个redis配置redis > [client …...

目标检测论文阅读:GaFPN算法笔记
标题:Construct Effective Geometry Aware Feature Pyramid Network for Multi-Scale Object Detection 会议:AAAI2022 论文地址:https://ojs.aaai.org/index.php/AAAI/article/view/19932 文章目录Abstract1. Introduction2. Related Work2.…...

【转】Generative Pretrained Transformer
原文链接:https://www.cnblogs.com/yifanrensheng/p/13167796.html一、GPT简介1.1 背景目前大多数深度学习方法依靠大量的人工标注信息,这限制了在很多领域的应用。此外,即使在可获得相当大的监督语料情况下,以无监督学习的方式学…...
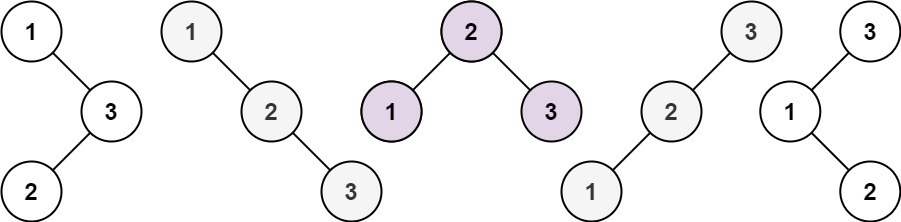
day34|343. 整数拆分、96.不同的二叉搜索树
343. 整数拆分 给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k > 2 ),并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。 示例 1: 输入: n 2 输出: 1 解释: 2 1 1, 1 1 1。 示例 2: 输入: n 10 输出: 36 解…...
WeNet - 初识
文章目录关于 WeNet快速上手识别训练环境准备训练关于 WeNet Production First and Production Ready End-to-End Speech Recognition Toolkit github: https://github.com/wenet-e2e/wenet官方中文说明:https://github.com/wenet-e2e/wenet/blob/main/README_CN.md…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...
