day34|343. 整数拆分、96.不同的二叉搜索树
343. 整数拆分
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
提示:
2 <= n <= 58
问题分析:
1、确定dp[i]数组以及下标的含义
dp[i]:拆解i,得到的最大乘积dp[i]
2、确定递推公式
有两种方式获得dp[i]
- j * ( i - j )(拆分i,拆成2份)
- j * dp[ i - j ]( 让i - j继续拆分,拆成3份及3份以上)
求最大乘积:dp[i]=Math.max(Math.max(j*(i-j),j*dp[i-j]),dp[i]);
最后max里加dp[i],因为是求整个dp[i]的最大值
3、dp数组初始化
n从2开始,所以dp[2]=1+1,1*1=1
4、确定遍历顺序
dp[i]依靠dp[i-j]的状态,所以从前往后
5、打印dp数组
class Solution {public int integerBreak(int n) {int[] dp=new int[n+1];dp[2]=1;for (int i=3;i<=n;i++){for (int j=1;j<i;j++){dp[i]=Math.max(Math.max(j*(i-j),j*dp[i-j]),dp[i]);}}return dp[n];}
}96.不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
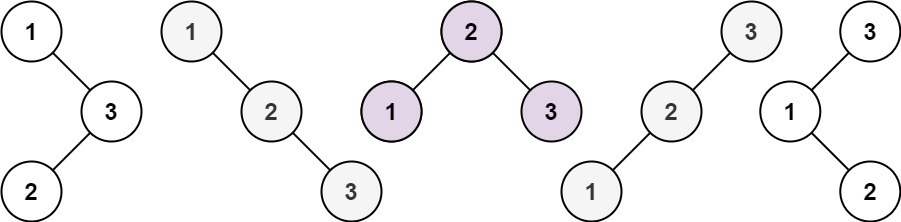
输入:n = 3
输出:5
示例 2:
输入:n = 1
输出:1
提示:
1 <= n <= 19
问题分析:
1、确定dp[i]数组以及下标的含义
dp[i]:1-i个节点组成的二叉搜索树的个数
2、确定递推公式
n=3:
1为头节点时,右子树有两个节点,布局和n=2时两棵树的布局一样(不关心数值,只关心布局)
2为头节点时,左子树有一个节点,右子树有一个节点,布局和n=1时一样
3为头节点时,左子树有两个节点,布局和n=2时两棵树的布局一样
dp[3]就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
有2个元素的搜索树数量就是dp[2]。
有1个元素的搜索树数量就是dp[1]。
有0个元素的搜索树数量就是dp[0]。
所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
递推公式:
dp[i]=dp[i]+dp[j]*dp[i-j-1]
j为左子树的节点数,i-j-1为右子树的节点数
3、dp数组初始化
dp[0]=1(空子树也为二叉搜索树),dp[1]=1
4、确定遍历顺序
dp[i]依靠dp[i-j-1]的状态,所以从前往后
5、打印dp数组
class Solution {public int numTrees(int n) {int[] dp = new int[n + 1];dp[0] = 1;//空节点也算二叉搜索树dp[1] = 1;for (int i = 2; i <= n; i++) {for (int j = 0; j < i; j++) {dp[i] = dp[i] + dp[j] * dp[i - j - 1];}}return dp[n];}}
相关文章:

day34|343. 整数拆分、96.不同的二叉搜索树
343. 整数拆分 给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k > 2 ),并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。 示例 1: 输入: n 2 输出: 1 解释: 2 1 1, 1 1 1。 示例 2: 输入: n 10 输出: 36 解…...
WeNet - 初识
文章目录关于 WeNet快速上手识别训练环境准备训练关于 WeNet Production First and Production Ready End-to-End Speech Recognition Toolkit github: https://github.com/wenet-e2e/wenet官方中文说明:https://github.com/wenet-e2e/wenet/blob/main/README_CN.md…...
为什么各个企业都在创建FAQ、常见问题页面?
常见问题解答页面是您可能已经为您的公司考虑过的东西,作为帮助客户回答有关您的产品和服务的常见问题的一种方式。但是您不知道最好的方法;肯定这只是一个问题清单吗?常见问题解答在整个购买过程中为客户提供支持,并减少客户需要与贵公司的联…...

【React-Router】路由传参,路由嵌套,手动导航,路由文件配置
文章目录React-RouterURL的hashHTML5的HistoryRouter的基本使用路由映射配置路由的嵌套路由配置和跳转Link和NavLink:手动路由的跳转路由参数传递Navigate导航Not Found页面配置路由的配置文件React-Router 前端路由是如何做到URL和内容进行映射呢?怎么…...
)
面向对象分析与设计(OOAD)
面向对象分析与设计(OOAD)概述人是怎么认识事物的分类与分层的两种思维问题域到解空间的映射软件生命周期要解决的问题三个一致性面向对象分析与设计过程对象从哪里来发现对象的方法组织对象结构职责是怎么来的分配职责的逻辑验证职责分配的合理性GRASP设…...

数据库调优
目录 硬件层面 操作系统层面 数据库层面 硬件层面 1.CPU(运算):48核CPU。 2.内存:96G-256G,跑3-4个实例。 3.disk(磁盘IO):机械盘:选SAS,数量越多越好。性能:SSD(高并发)>SAS(普通业务线上)>SATA(线下) 选SSD:使用SSD或者PCIe SSD设备,可提升上千倍的IOPS…...
 | 部署Glance)
OpenStack云平台搭建(3) | 部署Glance
目录 1、登录数据库授权 2、安装glance 3、测试一下 安装部署Glance镜像服务 Image Service 镜像服务:代号:Glance:为云平台虚拟机提供镜像服务,例如:上传镜像、删除镜像等。说明:镜像:磁盘…...

软件评测师考试总结
软件评测师是软考中级考试项,每年一次考试机会,2022年的是在11月份举行,具体事项需查看软考官网。 分享一下个人的备考经验,以及总结一下这个学习的过程,有需要的可以酌情参考。 一、方法策略 获取信息 官网&#x…...

小白系列Vite-Vue3-TypeScript:009-屏幕适配
上一篇我们介绍了ViteVue3TypeScript项目中mockjs的安装和配置。本篇我们来介绍屏幕适配方案,简单说来就是要最大程度上保证我们的界面在各种各样的终端设备上显示正常。通用的屏幕适配方案有两种:① 基于rem 适配(推荐,也是本篇要…...

查找企业微信聊天记录,会话存档有多重要
会话存档是基于企业微信API插口而开发设计的聊天记录查询专用工具。运用会话存档能不能找到误删除、到期的聊天记录呢?实际上能否通过会话存档找到企业微信中的聊天记录分两种状况,大家一起来看看吧:开启会话存档前的聊天记录没法找到和开启会…...
C语言经典编程题100例(1-20)
1、练习2-1 Programming in C is fun!本题要求编写程序,输出一个短句“Programming in C is fun!”。输入格式:本题目没有输入。输出格式:在一行中输出短句“Programming in C is fun!”。代码:#include<stdio.h> int main() {printf("Progra…...
小白系列Vite-Vue3-TypeScript:008-安装配置mock
上一篇我们介绍了ViteVue3TypeScript项目中axios的安装和配置,并手动封装了api。本篇我们来在上篇基础上介绍如何引入mock,并在本地模拟后台接口请求来达到本地测试的目的。在现在前后端分离的开发模式中,前端页面很多渲染的数据都需要通过ht…...

OnGUI Box 控件||Unity 3D OnGUI 常用控件
OnGUI Box 控件Unity 3D Box 控件用于在屏幕上绘制一个图形化的盒子。Box 控件中既可以显示文本内容,也可以绘制图片,或两者同时存在。GUIContent 和 GUIStyle 对于 Box 控件同样适用,既可以用来修饰 Box 控件的文本颜色,也可以用…...
shiro721——CVE-2019-12422
这两个漏洞主要区别在于Shiro550使⽤已知密钥碰撞,后者Shiro721是使⽤ 登录后rememberMe {value}去爆破正确的key值 进⽽反序列化,对⽐Shiro550条件只要有 ⾜够密钥库 (条件⽐较低)、Shiro721需要登录(要求⽐较⾼鸡肋 …...
爬虫JS逆向思路 - - 扣JS(data解密)
网络上几千块都学不到的JS逆向思路这里全都有👏🏻👏🏻👏🏻 本系列持续更新中,三连关注不迷路👌🏻 干货满满不看后悔👍👍👍 ❌注意…...
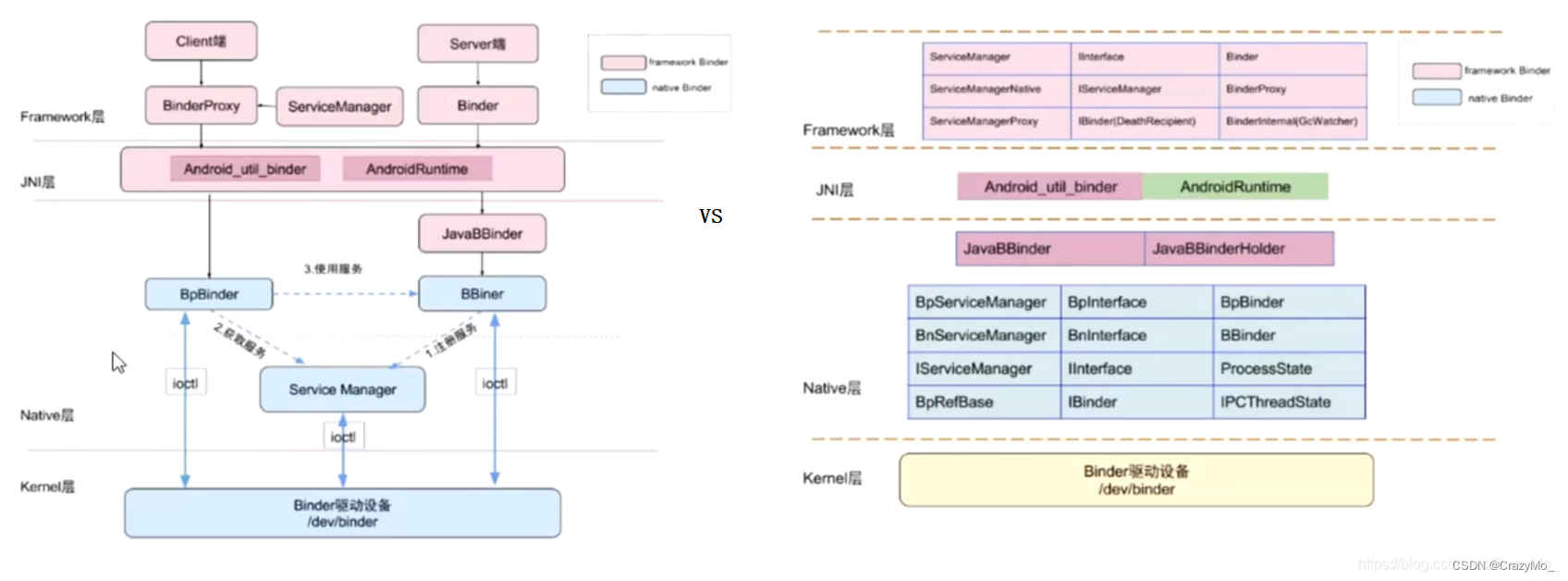
Android 进阶——Framework 核心之Binder 相关预备理论(一)
文章大纲引言一、进程的内存空间和进程隔离二、Linux 系统内存的用户空间和内核空间1、用户空间(User Space)2、内核空间(Kernel Space)三、Linux IPC 原理1、内核态和用户态2、IPC 步骤四、内核模块和驱动五、Binder1、Binder IP…...

【23种设计模式】结构型模式详细介绍
前言 本文为 【23种设计模式】结构型模式 相关内容介绍,下边将对适配器模式,桥接模式,组合模式,装饰模式,外观模式,亨元模式,代理模式,具体包括它们的特点与实现等进行详尽介绍~ &a…...
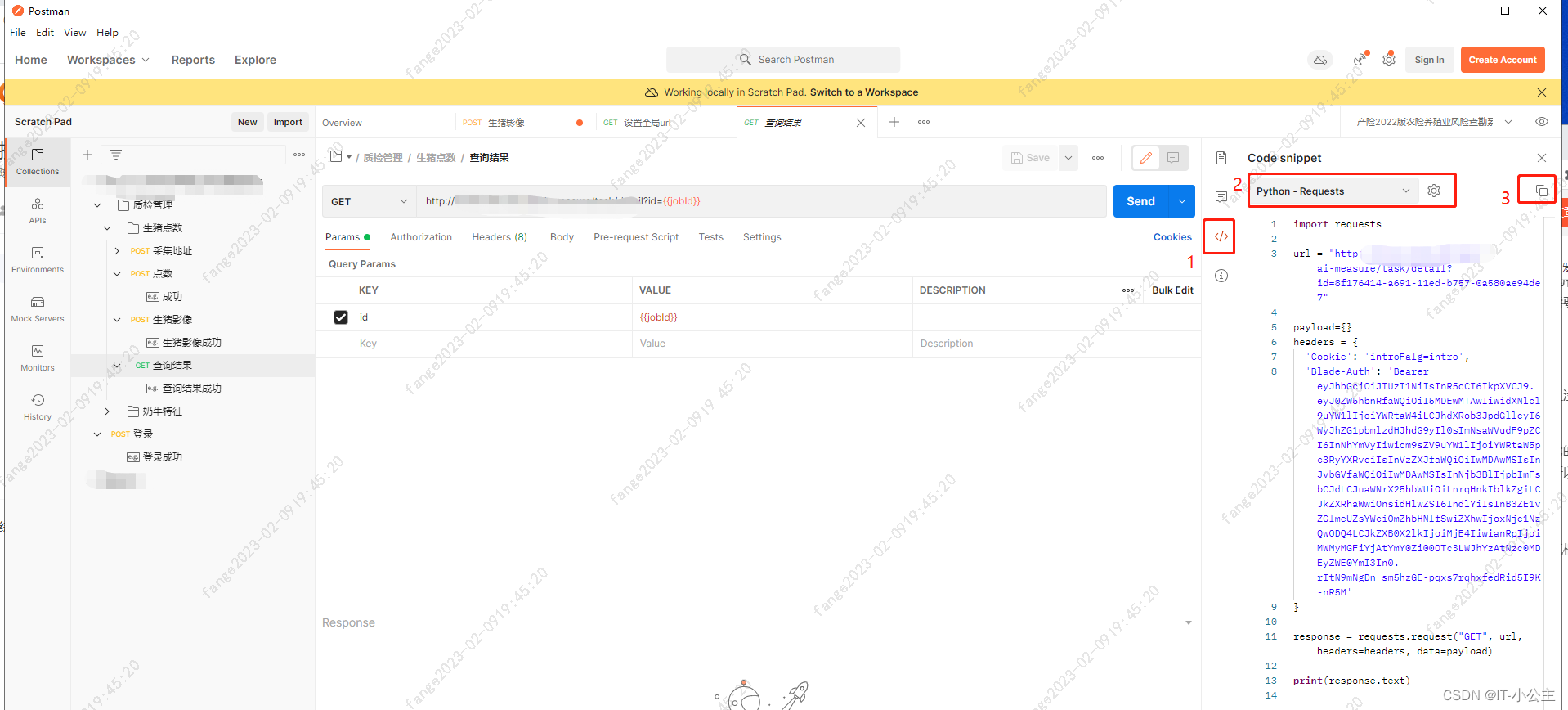
接口自动化实战-postman
1.测试模型 单元测试并非测试工程师的本职工作,它属于开发工程师的工作,开发进行单元测试的情况我们不知道,为了确保系统尽可能没有Bug,于是接口测试在测试工程师这里就变得由为重要了。实际工作中为菱形模型。 接口测试能更早的…...

前端跨域方案简单总结
1、什么是跨域 【】跨域是一种浏览器同源安全策略,也即浏览器单方面限制脚本的跨域访问。很多人可能误认为资源跨域时无法请求,实质上请求是可以正常发起的(指通常情况下,部分浏览器存在部分特例),后端也可…...
【HTML】HTML 表格 ② ( 表头单元格标签 | 表格标题标签 )
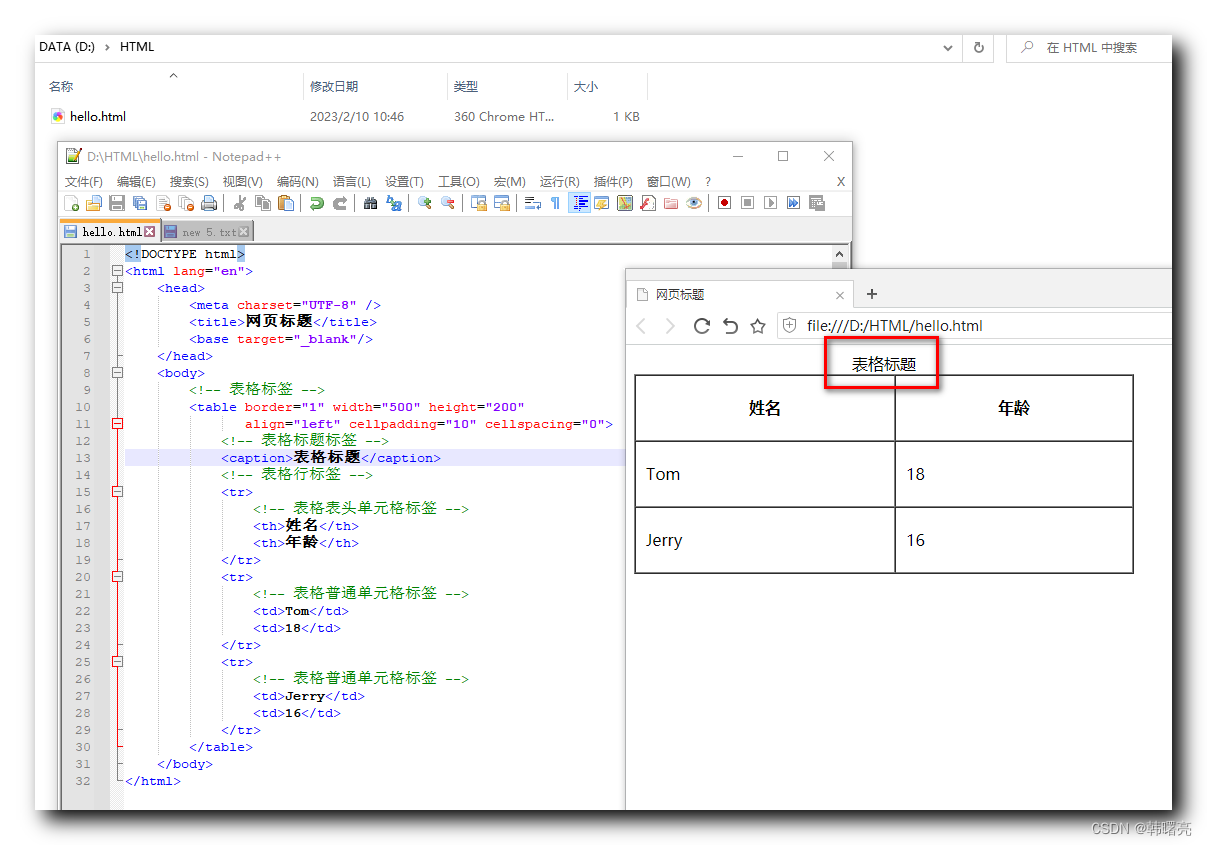
文章目录一、表头单元格标签二、表格标题标签一、表头单元格标签 表头单元格 可以在表格中 用作第一排 作为表格 的 表头 使用 , 表头单元格 中的 文本设置 可以与 普通单元格 中的文本设置 不同 ; 表头单元格 中的 文本 会 居中 , 并且 加粗 显示 ; 表头单元格 标签 如下 : &…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

数据结构:泰勒展开式:霍纳法则(Horner‘s Rule)
目录 🔍 若用递归计算每一项,会发生什么? Horners Rule(霍纳法则) 第一步:我们从最原始的泰勒公式出发 第二步:从形式上重新观察展开式 🌟 第三步:引出霍纳法则&…...
