C# 翻转二叉树
226 翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:

输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
示例 2:

输入:root = [2,1,3]
输出:[2,3,1]
示例 3:
输入:root = []
输出:[]
提示:
树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/invert-binary-tree
解决方案:
提供思路
我们从根节点开始,递归地对树进行遍历,并从叶子节点先开始翻转。如果当前遍历到的节点 root 的左右两棵子树都已经翻转,那么我们只需要交换两棵子树的位置,即可完成以 root 为根节点的整棵子树的翻转。
上代码:
/**
* Definition for a binary tree node.
* public class TreeNode {
* public int val;
* public TreeNode left;
* public TreeNode right;
* public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
public class Solution
{public TreeNode InvertTree(TreeNode root){if (root == null){return null;}InvertTree(root.left);InvertTree(root.right);TreeNode temp = root.left;root.left = root.right;root.right = temp;return root;}
}
个人感悟:题不难,别把自己吓住,是个节点切换的事。
以上是碰到的第二百二十六题,后续持续更新。感觉对你有帮助的小伙伴可以帮忙点个赞噢!

相关文章:

C# 翻转二叉树
226 翻转二叉树 给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。 示例 1: 输入:root [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1] 示例 2: 输入:root [2,1,3] 输出:…...
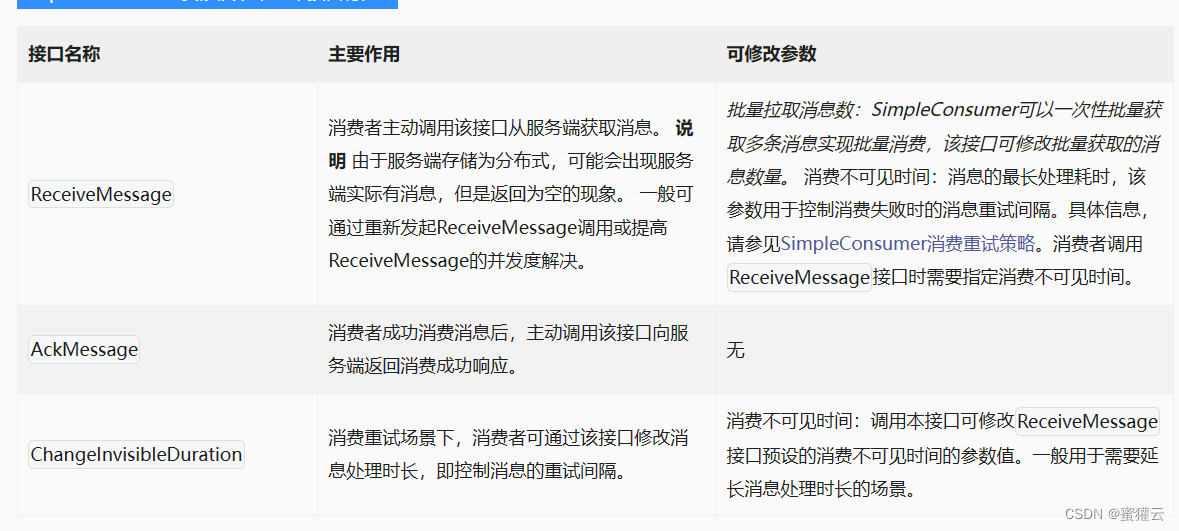
RocketMQ教程-(5)-功能特性-消费者分类
Apache RocketMQ 支持 PushConsumer 、 SimpleConsumer 以及 PullConsumer 这三种类型的消费者,本文分别从使用方式、实现原理、可靠性重试和适用场景等方面为您介绍这三种类型的消费者。 背景信息 Apache RocketMQ 面向不同的业务场景提供了不同消费者类型&…...
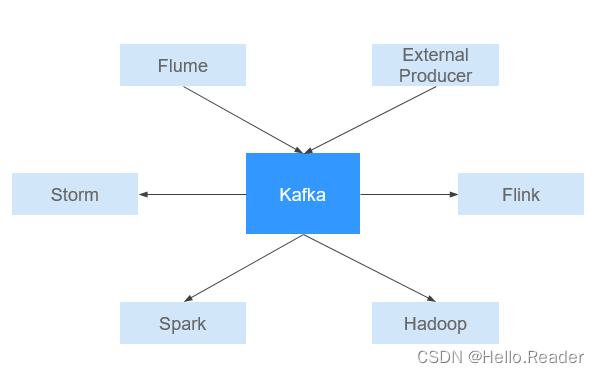
Kafka原理剖析
一、简介 Kafka是一个分布式的、分区的、多副本的消息发布-订阅系统,它提供了类似于JMS的特性,但在设计上完全不同,它具有消息持久化、高吞吐、分布式、多客户端支持、实时等特性,适用于离线和在线的消息消费,如常规的…...
word怎么转换成pdf?分享几种转换方法
word怎么转换成pdf?将Word文档转换成PDF文件有几个好处。首先,PDF文件通常比Word文档更容易在不同设备和操作系统上查看和共享。其次,PDF文件通常比Word文档更难以修改,这使得它们在需要保护文件内容的情况下更加安全可靠。最后&a…...

基于XDMA 中断模式的 PCIE3.0 QT上位机与FPGA数据交互架构 提供工程源码和QT上位机源码
目录 1、前言2、我已有的PCIE方案3、PCIE理论4、总体设计思路和方案图像产生、发送、缓存数据处理XDMA简介XDMA中断模式图像读取、输出、显示QT上位机及其源码 5、vivado工程详解6、上板调试验证7、福利:工程代码的获取 1、前言 PCIE(PCI Express&#…...
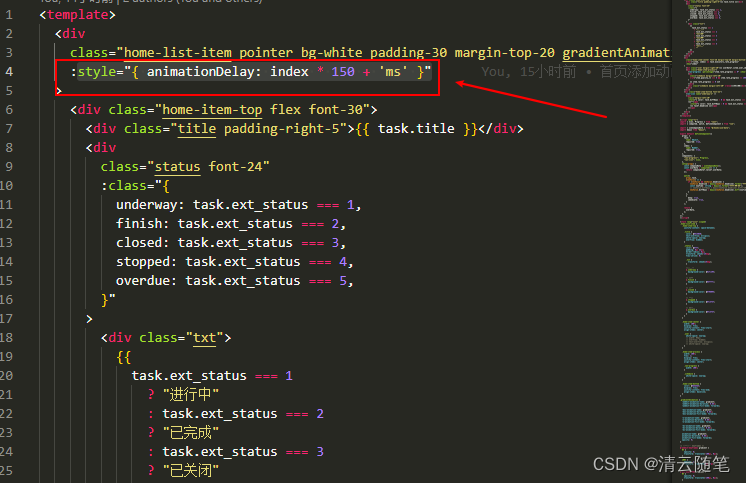
Vue 中通用的 css 列表入场动画效果
css 代码 .gradientAnimation {animation-name: gradient;animation-duration: 0.85s;animation-fill-mode: forwards;opacity: 0; }/* 不带前缀的放到最后 */ keyframes gradient {0% {opacity: 0;transform: translate(-100px, 0px);}100% {opacity: 1;transform: translate…...

微分流形2:流形上的矢量场和张量场
来了来了,切向量,切空间。流形上的所有的线性泛函的集合,注意是函数的集合。然后取流形上的某点p,它的切向量为,线性泛函到实数的映射。没错,是函数到实数的映射,是不是想到了求导。我们要逐渐熟…...
C++数组、向量和列表的练习
运行代码: //C数组、向量和列表的练习 #include"std_lib_facilities.h"int main() try {int ii[10] { 0,1,2,3,4,5,6,7,8,9 };for (int i 0; i < 10; i)//把数组中的每个元素值加2ii[i] 2;vector<int>vv(10);for (int i 0; i < 10; i)vv…...
视频剪辑矩阵分发系统Unable to load FFProbe报错技术处理?
问题一 报错处理 对于视频剪辑矩阵分发系统中出现的“Unable to load FFProbe”报错问题,可以采取以下技术处理措施进行解决。 1.检查系统中是否正确安装了FFProbe工具,并确保其路径正确配置。 2.检查系统环境变量是否正确设置,包括FFPr…...
Docker轻量级可视化工具Portainer
Portainer是一个轻量级的管理UI界面,用于管理Docker容器、镜像、卷和网络。它支持端口映射、容器启动、停止、删除、日志查看等功能,同时也提供了可视化的监控和统计功能,可以快速轻松的管理多个Docker主机。Portainer不需要额外安装依赖&…...

功率放大器在电光调制中的应用有哪些
电光调制是一种利用光电效应将电信号转化为光信号的技术。在实现电光调制的过程中,功率放大器作为一个重要的组件,具有对输入电信号进行放大和控制的功能。本文将介绍功率放大器的基本原理、特点以及在电光调制中的应用。 基本原理 功率放大器是一种能够…...

MyBatis入门程序
1.MyBatis 入门程序开发步骤 SqlSession:代表Java程序和数据库之间的会话。(HttpSession是Java程序和浏览器之间的会话) SqlSessionFactory:是“生产”SqlSession的“工厂”。 工厂模式:如果创建某一个对象ÿ…...

C++快速切换 头文件和源文件
有没有一种快速的方法 , 将头文件中的声明 直接在源文件中自动写出来, 毕竟头文件中已经有声明了, 我只需要写具体实现就行了,没有必要把声明的部分再敲一遍在 Visual Studio 中,你可以使用快速生成函数定义的功能来实…...
对原型、原型链的理解
在 JavaScript 中是使用构造两数来新建一个对象的,每一个构造函数的内部都有一个 prototype 属性,它的属性值是一个对象,这个对象包含了可以由该构造西数的所有实例共享的属性和方法。当使用构造函数新建一个对象后,在这个对象的内…...

7月26日,每日信息差
1、日本经产省将讨论让消费者负担核电站重启费。若被采用,那么即便是与把源自可再生能源作为卖点的新电力公司签约的消费者,也将负担重启核电站的费用 2、国家发改委:电厂存煤和出力均达历史同期最高水平 3、国家深改委:全国统调…...

git修改已经push后的commit注释
回到倒数第8次提交 git rebase -i HEAD~8修改注释,然后把最前面的pick改成edit 修改注释 git commit --amendrebase确认 git rebase --continue强制提交 git push -f origin master参考:https://blog.csdn.net/qq_16942727/article/details/1260355…...

网络云存储服务器,数据库服务器|PetaExpress
云存储服务器是什么? 云存储服务器是一种在线存储(英语:Cloud storage)该模式是将数据存储在通常由第三方托管的多个虚拟服务器上,而不是独家服务器上。 云存储服务器有几种结构 架构方法分为两类:一类是通过服务进行架构&…...

java语法基础--基本数据类型
一、数据类型概括 1、整数类型 2、浮点型 3、布尔类型 4、字符类型 二、数据类型的使用 1、整数类型的使用 超出类型范围 //1.1 定义一个byte类型的变量,并且设置它超过byte类型范围// 如果定义的数值在byte类型范围内,那么就能正常使用,//…...
uniapp 微信小程序 预览pdf方法
效果图: 1、在小程序中 // #ifdef MP */ 是区分运行的环境,在小程序中可使用如下方法uni.downloadFile({url: item.link,//文件地址success: function (res) {var filePath res.tempFilePath;uni.openDocument({filePath: filePath,showMenu: false…...
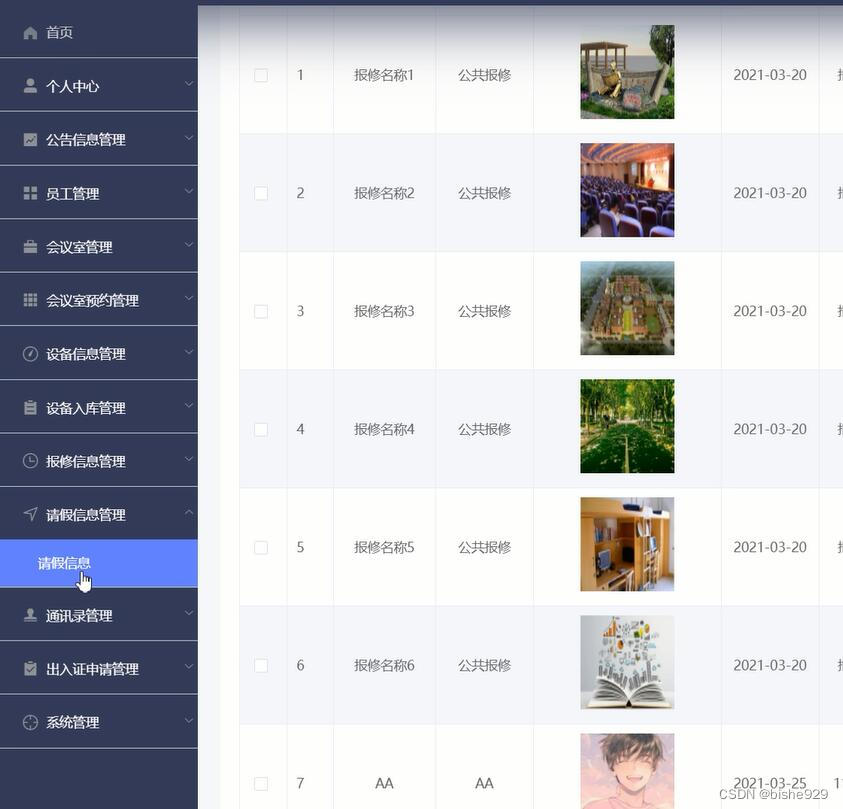
基于vue+uniapp微信小程序公司企业后勤服务(设备)系统
本系统分为用户和管理员两个角色,其中用户可以注册登陆系统,查看公司公告,查看设备,设备入库,查看通讯录,会议室预约,申请出入,申请请假等功能。管理员可以对员工信息,会…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
