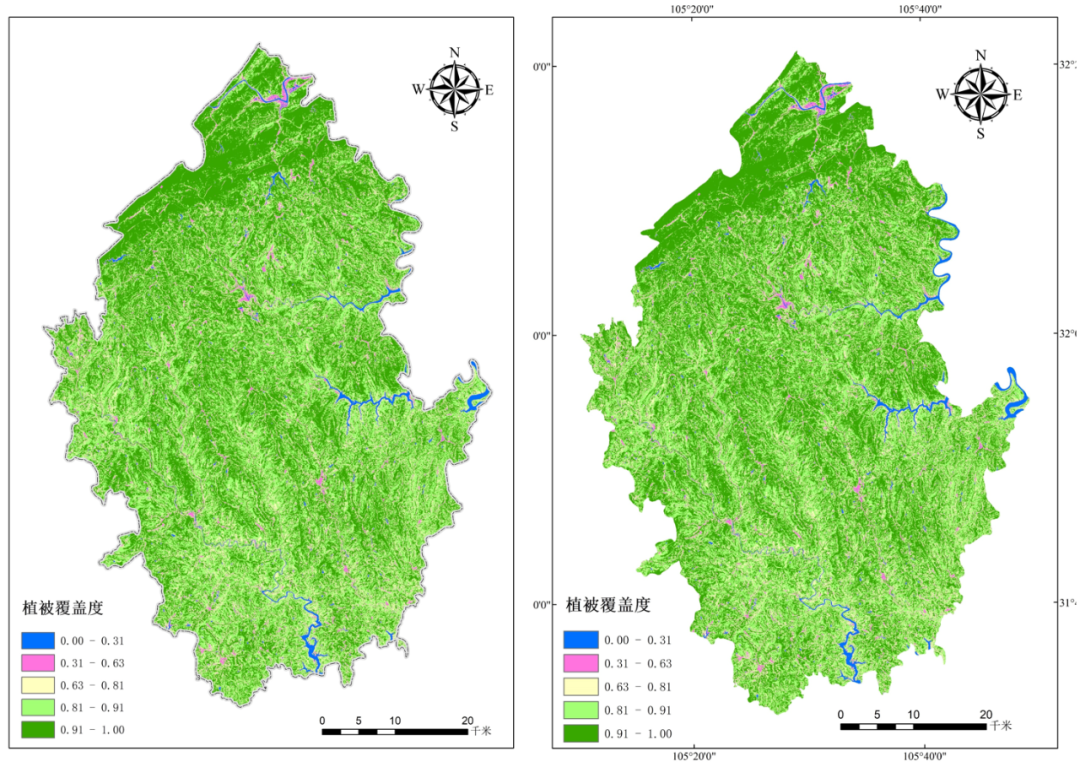
ENVI提取NDVI与植被覆盖度估算
目标是通过ENVI计算植被覆盖度结合ArcGIS出图得到植被覆盖图。
一、植被覆盖度的定义：
植被覆盖度( FractionalVegetation Cover，FVC) 通常定义为植被( 包括叶、茎、枝) 在地面的垂直投影面积占统计区总面积的百分比，它量化了植被的茂密程度，反应了植被的生长态势，是刻画地表植被覆盖的重要参数，也是指示生态环境变化的基本指标。植被覆盖度的测量方法从以前的地面测量（目估法、采样法等）操作复杂，成本高，效率低逐渐被遥感估算方法取代（回归指数、植被指数等）。
二、植被指数：
植被指数(vegeattinnhidxe)，又称光谱植被指数，是航天遥感应用于对地观测而提出的专业术语，是指由遥感传感器获取的多光谱数据，经线性和非线性组合而构成的对植被有一定指示意义的各种数值。
而NDVI(Nomralized Difference Vegeattion Idnex)—归一化植被指数,又称标准化植被指数。是植被指数的其中一种，也是植被覆盖度遥感估算方法中最常见、最经典的植被指数。所以这次实验是通过NDVI来估算植被覆盖度。
计算公式为:
NDVI=(NIR-R)/(NIR+R)
其中&#
相关文章：
ENVI提取NDVI与植被覆盖度估算
目标是通过ENVI计算植被覆盖度结合ArcGIS出图得到植被覆盖图。 一、植被覆盖度的定义： 植被覆盖度( FractionalVegetation Cover，FVC) 通常定义为植被( 包括叶、茎、枝) 在地面的垂直投影面积占统计区总面积的百分比，它量化了植被的茂密程度，反应了植被的生长态势，是刻画…...
Arm 扩大开源合作伙伴关系，加强投入开放协作
作者：Arm 开源软件副总裁 Mark Hambleton Arm 和我们的生态系统的关键信念之一是与开源社区合作，共创一个高度发达的 Arm 架构，使软件的落地更加稳定，从而让全球数百万开发者能够测试并创建自己的应用。 为此，Arm 支…...
Kubernetes 的核心概念：Pod、Service 和 Namespace 解析
🌷🍁 博主 libin9iOak带您 Go to New World.✨🍁 🦄 个人主页——libin9iOak的博客🎐 🐳 《面试题大全》 文章图文并茂🦕生动形象🦖简单易学！欢迎大家来踩踩~ἳ…...
互联网搜索的学习笔记
1. 参考资料 《Internet Search Tips》《Google Search Operators: The Complete List (42 Advanced Operators)》 2. 预备知识 2.1 查询语法 2.1.1 -：排除符 用于排除指定关键字。例如，如果想搜索“苹果”但不想看到“苹果手机”的结果，…...
vue事件修饰符
vue事件修饰符 1、目标2、语法 1、目标 在事件后面.修饰符名-给事件带来强大功能 2、语法 事件名.修饰符“methods里的函数” 修饰符列表 .stop - 阻止事件冒泡 示例： <template><div id"app"><div click"fatherFn"><…...
【安全】web中的常见编码浅析浏览器解析机制
目录 常见编码 一、ASCII码 二、URL编码 三、Unicode编码 四、HTML实体编码 结合编码理解浏览器解析机制 常见编码 一、ASCII码 ASCII (American Standard Code for Information Interchange，美国信息交换标准代码） 计算机内部࿰…...
Ceph概述、准备ceph部署环境、cephadm概述、安装Ceph集群、ceph块存储、存储池、rbd镜像管理、ceph客户端配置
day03 day03ceph概述部署Ceph节点准备cephadm准备基础环境安装ceph实现块存储块存储基础存储池镜像ceph客户端 ceph概述 ceph可以实现的存储方式： 块存储：提供像普通硬盘一样的存储，为使用者提供“硬盘”文件系统存储：类似于NFS…...
python selenium爬虫自动登录实例
拷贝地址：python selenium爬虫自动登录实例_python selenium登录_Ustiniano的博客-CSDN博客 一、概述 我们要先安装selenium这个库，使用pip install selenium 命令安装，selenium这个库相当于机器模仿人的行为去点击浏览器上的元素࿰…...
el-cascader 数据的回显
<el-cascaderplaceholder"试试搜索":options"allOptions":props"{ multiple: true }"v-model"options"filterable style"width: 80%;max-height:240px;overflow-y:scroll;"></el-cascader> allOptions里面包含…...
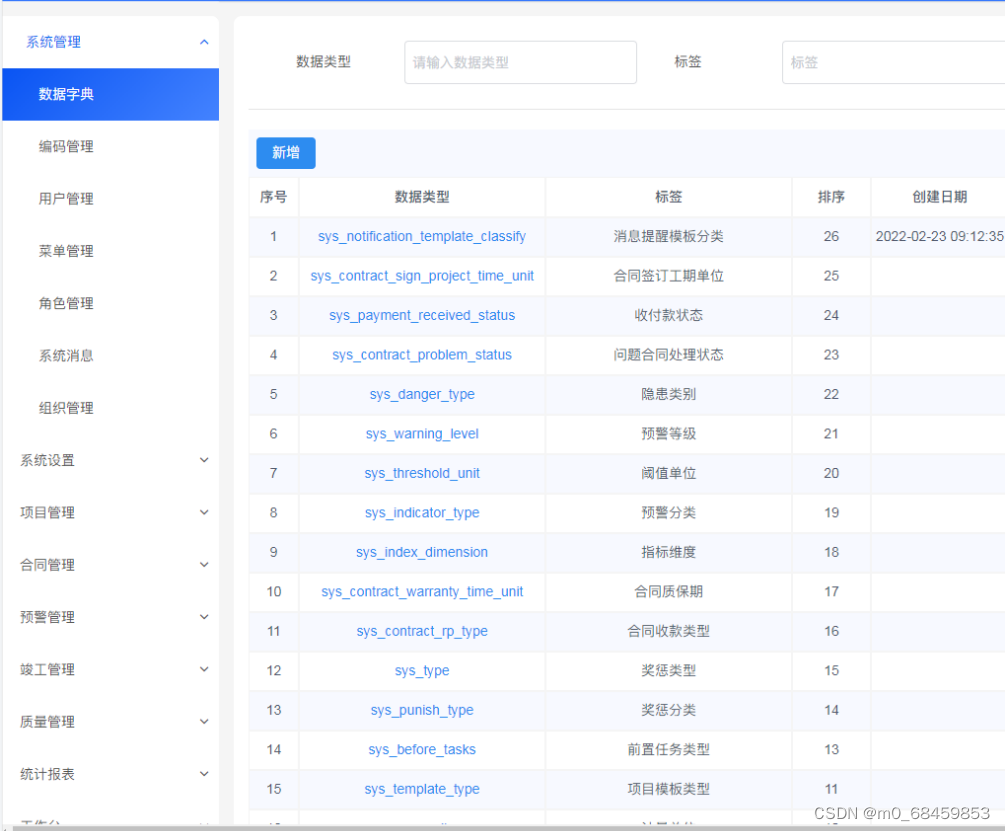
Java 版 spring cloud +spring boot 工程系统管理 工程项目管理系统源码 工程项目各模块及其功能点清单
工程项目各模块及其功能点清单 一、系统管理 1、数据字典：实现对数据字典标签的增删改查操作 2、编码管理：实现对系统编码的增删改查操作 3、用户管理：管理和查看用户角色 4、菜单管理：实现对系统菜单的增删改查操…...
即时通信的方法和webSocket的具体使用
前言 之前遇到过需要即时通讯的场景，刚开始使用的是通过轮询的方式，定时器3秒向服务器请求一次数据，后面发现如果在手机端长时间打开使用此功能的页面，可能会发生手机发热，甚至卡顿的现象。最后改用webSocket…...
HTML 速查列表
HTML 速查列表 HTML 速查列表. 你可以打印它，以备日常使用。 HTML 基本文档 <!DOCTYPE html> <html> <head> <title>文档标题</title> </head> <body> 可见文本... </body> </html> 基本标签（Ba…...
Hadoop集成Hive
一、环境与软件准备 说明：服务器已用主机名代替，可根据自己的需求，改为IP地址 环境 服务器组件masterNameNode、DataNode、Nodemanager、ResourceManager、Hive、Hive的metastore、Hive的hiveserver2、mysqlSecondarySecondaryNameNode、D…...
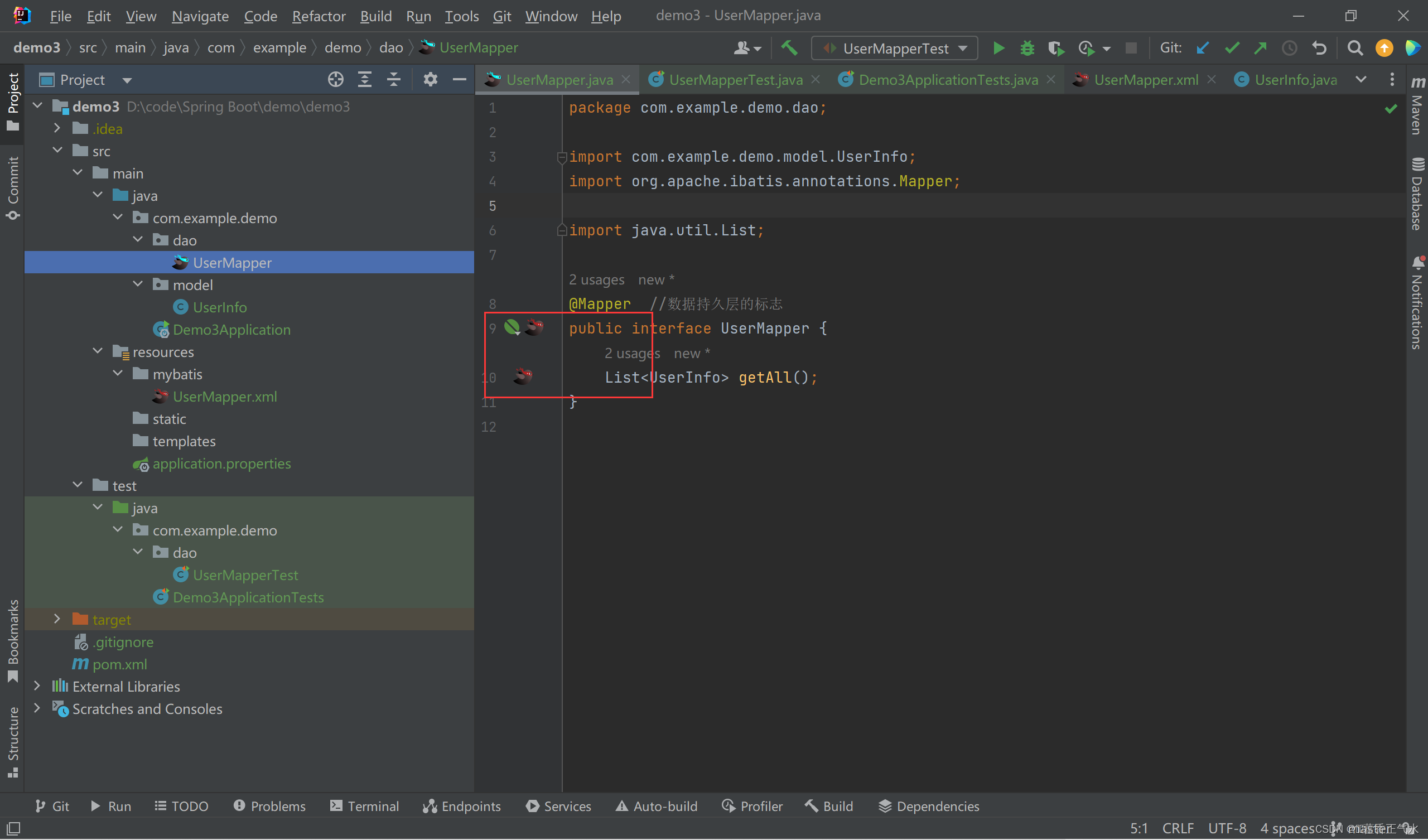
MyBatis查询数据库
目录 一、什么是MyBatis 二、搭建MyBatis开发环境 🍅添加MyBatis依赖 🍅在数据库添加数据 🍅设置MyBatis配置 🎈数据库的相关连接信息🎈xml的保存和设置路径 三、使用MyBatis模式和语法操作数据库 ἴ…...
RVM问题记录 - Error running ‘__rvm_make -j10‘
文章目录 前言开发环境问题描述问题分析解决方案最后 前言 公司新到一台电脑需要配置开发环境，在用RVM安装Ruby时遇到了一个奇怪的问题。 开发环境 RVM: 1.29.12OpenSSL: 3.1.1 问题描述 执行命令安装Ruby 3.0版本： rvm install ruby-3.0.0在编译阶…...
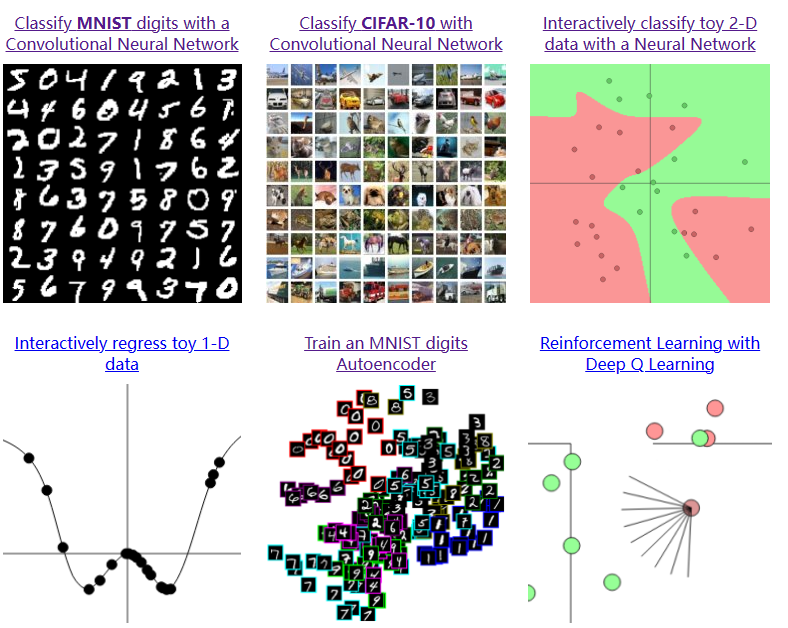
VIS for AI ：ConvNetJS
1.简单介绍： ConvNetJS是由斯坦福大学计算机科学系的Andrej Karpathy开发的一个深度学习框架，用于在浏览器中运行卷积神经网络（ConvNet）。ConvNetJS可以帮助开发人员在客户端（浏览器）上进行深度学习任务&a…...
【Python入门系列】第二十篇：Python区块链和加密货币
文章目录 前言一、区块链基础知识1.1 什么是区块链1.2 区块链的工作原理 1.3 区块链的优势和应用场景二、Python实现区块链2.1 创建区块类2.2 创建区块链类2.3 添加区块和验证区块链 三、加密货币基础知识3.1 什么是加密货币3.2 加密货币的工作原理3.3 加密货币的挖矿和交易 四…...
MySQL 服务器的调优策略
点击上方↑“追梦 Java”关注，一起追梦！ 在工作中，我们发现慢查询一般有2个途径，一个是被动的，一个是主动的。被动的是当业务人员反馈某个查询界面响应的时间特别长，你才去处理。主动的是通过通过分析慢查询…...
)
Educational Codeforces Round 152 (Rated for Div. 2)
B这个题目在20分钟的时候发现了取模的规律，但是在写法上我竟然犹豫了，这影响了我后面题目的心态 过于可惜了 但是没关系，现在不会，之后就会写了 这里强调一下，sort不会改变原先的顺序，就是说如果两个相等的…...
CSPM难度大吗？对比pmp怎么样？
CSPM证书是刚出来的，难度不会很大，大家都知道 PMP 证书是从国外引进的，近几年很热门，持证人数已经高达 90 余万了，但是目前我们和老美关系大家有目共睹，一直推国际标准和美国标准感觉有点奇怪。 现在新出台…...
DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增：通道注意力模块（SE模块） class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...
渗透实战PortSwigger靶场-XSS Lab 14：大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet： https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...
oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异，它们的数据同步要求既要保持数据的准确性和一致性，又要处理好性能问题。以下是一些主要的技术要点： 数据结构差异 数据类型差异ÿ…...
鱼香ros docker配置镜像报错：https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题：docker pull 失败 网络不同，需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...
NLP学习路线图（二十三）：长短期记忆网络（LSTM）
在自然语言处理（NLP）领域，我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感，还是实现语言的翻译，都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心，而循环神经网络（RNN） 曾被视为…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战：借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中，性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期，开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发，但背后往往隐藏着系统资源调度不当…...
Go 并发编程基础：通道（Channel）的使用
在 Go 中，Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式，用于在多个 Goroutine 之间传递数据，从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...
MFC 抛体运动模拟：常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时，我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点，详细解析原因并提供解决方案，同时兼顾界面美化，让模拟效果更专业、更高效。 问题一：历史轨迹与小球残影残留 现象 小球运动后，历史位置的 “残影”…...
【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下，限制某个 IP 的访问频率是非常重要的，可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案，使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值，最大值左侧的数值严格单调递增，最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值，最小值左侧的数值严格单调递减，最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...