Codeforces Round 888 (Div. 3)(A-F)
文章目录
- A
- B
- C
- D
- E
- F
A
题意:
就是有一个m步的楼梯。每一层都有k厘米高,现在A的身高是H,给了你n个人的身高问有多少个人与A站在不同层的楼梯高度相同。
思路:
我们只需要去枚举对于A来说每一层和他一样高(人的身高和楼梯高度)的人数即可。
代码:
#include<bits/stdc++.h>#define IOS ios::sync_with_stdio(false);cin.tie(nullptr)
#define int long long
#define endl "\n"
#define xx first
#define yy secondusing namespace std;const int N = 2e5 + 10, mod = 1e9 + 7;int n, m, k, _, h;
int arr[N];void solve()
{cin >> n >> m >> k >> h;map<int, int> mp;for(int i = 1; i <= n; i ++) {cin >> arr[i];mp[arr[i]]++;}int ans = 0;for(int i = 1; i < m; i ++){ans += mp[i*k+h];ans += mp[-i*k+h];}cout << ans << endl;
}signed main()
{IOS;cin >> _;while(_--) solve(); return 0;
}
B
题意:
就是给你n个数,你需要把这n个数变成非降序即可,但是只能奇数和奇数之间进行位置交换,偶数和偶数之间进行位置交换。
思路:
我们对于每一个奇数和偶数记录下他们的大小和位置,对于奇数和偶数让他们各自内部排序。然后回到他们各自内部排序的位置。
比如:
num: 7 10 1 3 2
ip : 1 2 3 4 5
然后我们让奇数和偶数各自内部排序:
奇数:
num:1 3 7
ip : 1 3 4
偶数:
num:2 10
ip :5 2
结果:
1 2 3 7 10
然后按照各自排序的ip重新拼在一起看是否是一个非降序数列就行。
代码:
#include<bits/stdc++.h>#define IOS ios::sync_with_stdio(false);cin.tie(nullptr)
#define int long long
#define endl "\n"
#define xx first
#define yy secondusing namespace std;const int N = 1e6 + 10, mod = 1e9 + 7;int n, m, k, _, h;
int arr[N];void solve()
{cin >> n;for(int i = 1; i <= n; i ++) cin >> arr[i];vector<int> odd, even, ipodd, ipeven;for(int i = 1; i <= n; i ++){if(arr[i] & 1){odd.push_back(arr[i]);ipodd.push_back(i);}else{even.push_back(arr[i]);ipeven.push_back(i);}}sort(odd.begin(), odd.end());sort(even.begin(), even.end());sort(ipodd.begin(), ipodd.end());sort(ipeven.begin(), ipeven.end());vector<int> ans(n+1);for(int i = 0; i < odd.size(); i ++){ans[ipodd[i]] = odd[i];}for(int i = 0; i < even.size(); i ++){ans[ipeven[i]] = even[i];}bool f = 0;for(int i = 2; i <= n; i ++){if(ans[i] < ans[i-1]){f= 1;break;`在这里插入代码片`}}if(f) cout << "NO" << endl;else cout << "YES" << endl;
}signed main()
{IOS;cin >> _;while(_--) solve(); return 0;
}
C
这道题纯纯阅读理解,就直接说思路了。
思路:
就是你要找k个第一个数(用a来表示,从前往后找)然后对于最后一个a的位置我们用l来表示,然后你要找到k个最后一个数(用b来表示,从后往前找)对于从后往前的最后一个b的位置我们用r来表示。如果l > r无解,如果对于a,b只要一个没有找到k个无解。否则就输出YES就行。如果第一个数和第二个数相等只需要找出k个就行
代码:
#include<bits/stdc++.h>#define IOS ios::sync_with_stdio(false);cin.tie(nullptr)
#define int long long
#define endl "\n"
#define xx first
#define yy secondusing namespace std;const int N = 1e6 + 10, mod = 1e9 + 7;int n, m, k, _, h;
int arr[N];void solve()
{cin >> n >> k;int l = 0, cnt = 0;bool fl = 0, fr = 0;for(int i = 1; i <= n; i ++) cin >> arr[i];for(int i = 1; i <= n; i ++){if(arr[i] == arr[1] && cnt < k) cnt++;if(cnt == k){fl = 1;l = i;break;}}int r = n;cnt = 0;for(int i = n; i >= 1; i --){if(arr[i] == arr[n] && cnt < k){cnt++;}if(cnt == k){fr = 1;r = i;break;}}if(arr[1] == arr[n]){if(fl || fr){cout << "YES" << endl;return;}}if(!fl || !fr){cout << "NO" << endl;return;}if(l > r){cout << "NO" << endl;return;}cout << "YES" << endl;
}signed main()
{IOS;cin >> _;while(_--) solve(); return 0;
}
D
这个题当时脑壳瓦特了,直接特判了如果差分数组出现了两个及以上就无解。
题意:
就是现在给你n-1个数这几个数是n个数的前缀和数组,其中少了一个。问你是否存在n个数的前缀和数组满足这n-1个数。这n个数是1~n的。
思路:
其实我们只用看这n-1个数的差分数组,然后我们就可以去还原数组了。那么我们再去判断差分数组中出现1~n的个数。如果差了一个,那么一定有解。如果差了两个我们就去看一下这两个数之和,是不等于大于n的那个数(差分数组里的数),或者是出现了两次的数字之和(差分数组里的数出现了两次)。如果不等于也是无解。如果等于那就是有解。如果差了两个以上那么一定是无解的。
代码:
#include<bits/stdc++.h>#define IOS ios::sync_with_stdio(false);cin.tie(nullptr)
#define int long long
#define endl "\n"
#define xx first
#define yy secondusing namespace std;const int N = 1e6 + 10, mod = 1e9 + 7;int n, m, k, _, h;void solve()
{cin >> n;vector<int> arr(n+1);int ma = 0, mi = 1e18;map<int, int> cnt;for(int i = 1; i < n; i ++) {cin >> arr[i];ma = max(arr[i], ma);mi = min(arr[i], mi);} vector<int> g(n+1);map<int, int> fg;for(int i = 1; i < n; i ++){g[i] = arr[i]-arr[i-1];fg[g[i]]++;}int sum = 0;int ct = 0;for(int i = 1; i <= n; i ++){if(!fg[i]) {sum += i;ct++;}}if(ct == 1){cout << "YES" << endl;return;}if(ct > 2){cout << "NO" << endl;return;}int tp = 0;for(int i = 1; i < n; i ++){if(fg[g[i]] >= 2) tp = g[i];else if(g[i] > n) tp = g[i];}if(sum == tp){cout << "YES" << endl;}else cout << "NO" << endl;
}signed main()
{IOS;cin >> _;while(_--) solve(); return 0;
}
E
题意:
就是你需要配制出n种药水,然后给你n种药水直接购买的花费价值。对于一些药水会提供无数种对于这一类药水的花费价值是0,那么没有提供无限次数的药水需要自己去通过配方配置或者直接购买。保证不会出现环,就是a只能配置b,b只能配置a。问你配置出所有药水的最小价值。
思路:
记忆化搜索,对于每种可以配置的药水我们给他进行建图单向图,因为保证不会出现环的,那么我们最后去遍历那些没有别确定价值的药水,然后去记忆化搜索下去就行。
队友写的是BFS,他这种写法就是能够处理环的。
代码:
#include<bits/stdc++.h>#define IOS ios::sync_with_stdio(false);cin.tie(nullptr)
#define int long long
#define endl "\n"using namespace std;const int N = 2e5 + 10;int n, m, k, _;
int c[N], p[N];
vector<int> e[N];
map<int, bool> f;
void dfs(int x)
{int res = 0;if(e[x].size() == 0){f[x] = 1;return;}for(int i = 0; i < e[x].size(); i ++){int g = e[x][i];if(!f[g]){dfs(g);res += c[g];}else res += c[g];}f[x] = 1;c[x] = min(c[x], res);
}void solve()
{f.clear();cin >> n>> k;for(int i = 1; i <= n; i ++){cin >> c[i];e[i].clear();}for(int i = 1; i <= k; i ++){int x;cin >> x;f[x] = 1;c[x] = 0;}for(int i = 1; i <= n; i ++){int x;cin >> x;while(x--){int g;cin >> g;e[i].push_back(g);}}for(int i = 1; i <= n; i ++){if(!f[i]) dfs(i);cout << c[i] << " ";}cout << endl;
}signed main()
{IOS;cin >> _;while(_--) solve();return 0;
}
F
#include <bits/stdc++.h>
//#define int long long
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define endl '\n'
#define lb(x) ((x) & (-x))
using namespace std;
typedef unsigned long long ull;
const int maxn = 2e5+10;
const int mod = 2e9+7;
const ull P = 13331;
int _,n,m,k;
int tr[maxn * 32][2],idx;
void add(int x)
{int p = 0;for(int i = k-1; i >= 0; --i){int z = (x >> i) & 1;if(!tr[p][z]) tr[p][z] = ++idx;p = tr[p][z];}
}
int get(int x)
{int p = 0,ans = 0;for(int i = k-1; i >= 0; --i){int z = (x >> i) & 1;if(tr[p][z]) p = tr[p][z];else p = tr[p][1-z],ans += (1LL << i);}return ans;
}
void clear()
{for(int i = 0; i <= idx; ++i){for(int j = 0; j <= 1; ++j) tr[i][j] = 0;}idx = 0;
}
signed main()
{IOS;cin >> _;while(_--){clear();cin >> n >> k;vector<int> a(n+1);map<int,vector<int> > mp;int mx = mod;for(int i = 1; i <= n; ++i){cin >> a[i];mp[a[i]].push_back(i);if(i > 1) mx = min(mx,get(a[i]));add(a[i]);}int x = 0,y = 0;for(int i = 1; i <= n; ++i){int g = (mx^a[i]);if(g != a[i] && mp[g].size() > 0) x = i,y = mp[g][0];else if(g == a[i] && mp[g].size() > 1){x = i;if(mp[g][0] != i) y = mp[g][0];else y = mp[g][1];}}int z = 0;for(int i = k-1; i >= 0; --i){if(((a[x] >> i) & 1) == 0) z += (1LL << i);}cout << x << ' ' << y << ' ' << z << endl;}return 0;
}
相关文章:
(A-F))
Codeforces Round 888 (Div. 3)(A-F)
文章目录 ABCDEF A 题意: 就是有一个m步的楼梯。每一层都有k厘米高,现在A的身高是H,给了你n个人的身高问有多少个人与A站在不同层的楼梯高度相同。 思路: 我们只需要去枚举对于A来说每一层和他一样高(人的身高和楼…...
、多卷积核、全连接、池化)
【人工智能】深度神经网络、卷积神经网络(CNN)、多卷积核、全连接、池化
深度神经网络、卷积神经网络(CNN)、多卷积核、全连接、池化) 文章目录 深度神经网络、卷积神经网络(CNN)、多卷积核、全连接、池化)深度神经网络训练训练深度神经网络参数共享卷积神经网络(CNN)卷积多卷积核卷积全连接最大池化卷积+池化拉平向量激活函数优化小结深度神经…...

失去SSL证书,会对网站安全造成什么影响?
作为网络世界中的“身份证”,SSL证书可以在网络世界中证明你是一个真实可信的企业或个人网站,而不是一个钓鱼网站。且在网站的服务器上部署SSL证书后,可以使网站与访问者之间通过SSL协议建立安全的加密连接,确保在Web服务器和浏览…...

gitee中fork了其他仓库,如何在本地进行同步
GitHub 操作:同步 Fork 来的仓库(上游仓库)_sigmarising的博客-CSDN博客 1. 设置upstream 2. git pull --rebase 3. 然后再执行pull、push操作...
java项目之社区生活超市管理系统(ssm+mysql+jsp)
风定落花生,歌声逐流水,大家好我是风歌,混迹在java圈的辛苦码农。今天要和大家聊的是一款基于ssm的社区生活超市管理系统。技术交流和部署相关看文章末尾! 开发环境: 后端: 开发语言:Java 框…...
:C++头部封装)
WebGPU(七):C++头部封装
WebGPU(七):C头部封装 在前面的学习中,我们使用的都是原生态的WebGPU API,那是基于C语言的API,但是为了更高效的开发,我们可以使用一个基于C的库。 根据参考的教程,这个github库提供更加纤细的描述。它提…...

Linux 网络通信epoll详解( 10 ) -【Linux通信架构系列 】
系列文章目录 C技能系列 Linux通信架构系列 C高性能优化编程系列 深入理解软件架构设计系列 高级C并发线程编程 期待你的关注哦!!! 现在的一切都是为将来的梦想编织翅膀,让梦想在现实中展翅高飞。 Now everything is for the…...

java源码-List源码解析
Java中的List是一个接口,它定义了一组操作列表的方法。List接口的常见子类包括ArrayList、LinkedList和Vector等。 以下是Java中List接口及其常见方法的源码解析: 1. List接口定义 public interface List<E> extends Collection<E> { …...

Mybatis的动态SQL
动态 sql 是Mybatis的强⼤特性之⼀,能够完成动态的 sql 语句拼接。 动态 SQL 大大减少了编写代码的工作量,更体现了 MyBatis 的灵活性、高度可配置性和可维护性。 Mybatis里的动态标签主要有: <if><trim><where><set><forea…...
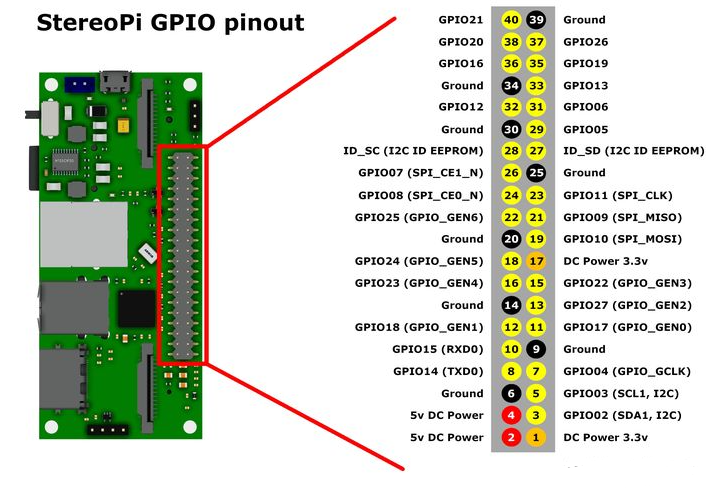
嵌入式系统中的GPIO控制:从理论到实践与高级应用
本文将探讨嵌入式系统中的GPIO(通用输入输出)控制,着重介绍GPIO的原理和基本用法。我们将使用一个实际的示例项目来演示如何通过编程配置和控制GPIO引脚。将基于ARM Cortex-M微控制器,并使用C语言进行编写。 GPIO是嵌入式系统中最常见且功能最强大的接口之一。它允许硬件工…...

7D透明屏的市场应用广泛,在智能家居中有哪些应用表现?
7D透明屏是一种新型的显示技术,它能够实现透明度高达70%以上的显示效果。这种屏幕可以应用于各种领域,如商业广告、展览展示、智能家居等,具有广阔的市场前景。 7D透明屏的工作原理是利用光学投影技术,将图像通过透明屏幕投射出来…...

[游戏开发][Unity] 打包Xcode工程模拟器+真机调试
苹果开发者账号 账号分三类,个人,公司,企业,价格99/99/299美金 新注册账号的基本设置按网上的教程来就行 我们公司是企业账号,我的苹果开发者账号是公司一个User 下面讲述一下一个全新的打包机处理流程 首先是要把…...

python 添加环境变量
1 查看是否设置环境变量 和 使用的python在哪里安装 import sys import os# 获取Python的安装目录 import os import syspython_path sys.executable # 这个是python.exe的路径python_path os.path.dirname(python_path) print("Python安装路径:", python_path)# …...
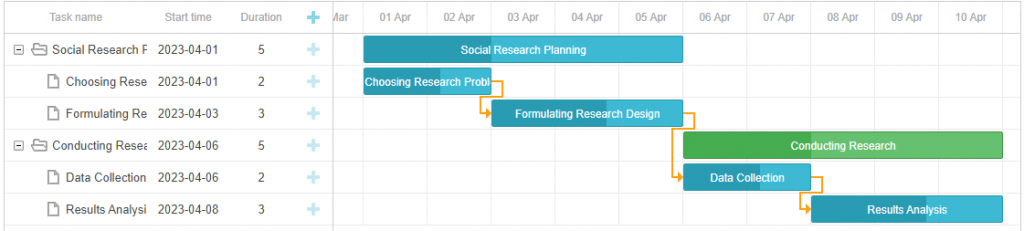
如何用DHTMLX组件为Web应用创建甘特图?(一)
dhtmlxGantt是用于跨浏览器和跨平台应用程序的功能齐全的Gantt图表。可满足项目管理应用程序的所有需求,是最完善的甘特图图表库。甘特图仍然是项目管理应用程序中最需要的工具之一,DHTMLX Gantt组件提供了能提升研发甘特图功能所需的重要工具。 在这篇…...

网站SEO优化:提升搜索排名与流量引爆
导言: 在互联网时代,网站SEO(搜索引擎优化)是提高网站搜索排名、吸引流量、增加曝光的重要策略。通过优化网站结构、内容和链接等方面,让搜索引擎更好地理解和收录网站内容,从而为网站带来更多有价值的有机…...

Java lamda对List<JSONObject>里多个动态属性字段进行动态的降序或者升序
最近做到一个需求,需要把业务侧返回的数据(格式为List<JSONObject>),然后根据前端传来的排序字段、以及升降序属性来排序并返回给前端。要对List<JSONObject>中的多个属性字段进行动态的升序或降序排序,我们可以根据需…...

Lua脚本解决多条命令原子性问题
Redis是一个流行的键值存储数据库,它提供了丰富的功能和命令。在Redis中,我们可以使用Lua脚本来编写多条命令,以确保这些命令的原子性执行。Lua是一种简单易学的编程语言,下面将介绍如何使用Redis提供的调用函数来操作Redis并保证…...
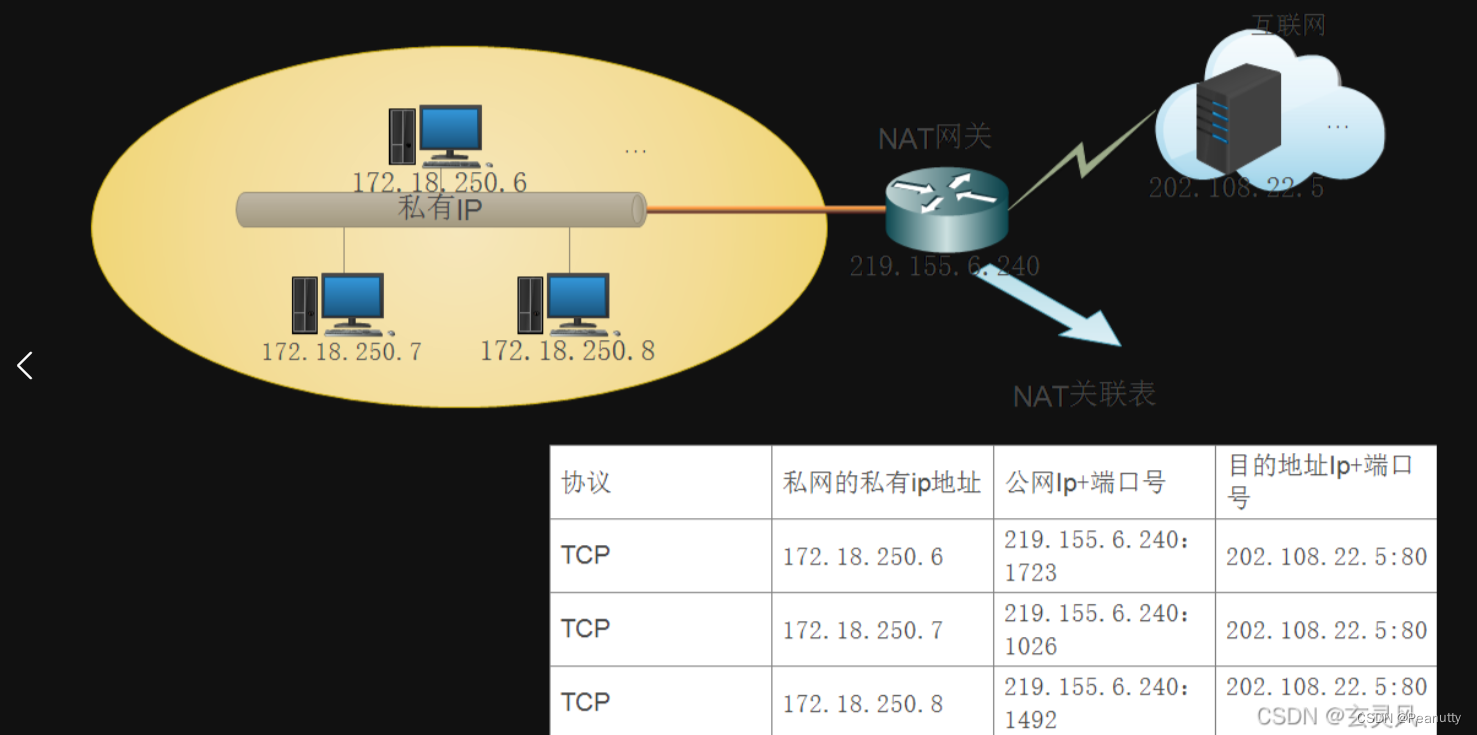
NAT详解(网络地址转换)
一句话说清楚它是干什么的: 网络地址转换:是指通过专用网络地址转换为公用地址,从而对外隐藏内部管理的IP地址,它使得整个专用网只需要一个全球IP就可以访问互联网,由于专用网IP地址是可以重用的,所以NAT大…...

【第一阶段】ktolin的函数
在Java中我们称之为方法,方法必须写在类里面,依赖于类。 在kotlin中函数写在类里面和外面都是可以的。称之为函数 class test{fun view(){} }fun main() {println("Hello, world!!!") }执行结果 Hello, world!!!main函数的返回值类型为Unit等…...

pytorch模型的保存与加载
1 pytorch保存和加载模型的三种方法 PyTorch提供了三种种方式来保存和加载模型,在这三种方式中,加载模型的代码和保存模型的代码必须相匹配,才能保证模型的加载成功。通常情况下,使用第一种方式(保存和加载模型状态字…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
