【算法基础:搜索与图论】3.5 求最小生成树算法(PrimKruskal)
文章目录
- 最小生成树介绍
- 朴素Prim算法
- 算法思路⭐
- 例题:858. Prim算法求最小生成树
- Kruskal算法
- 算法思路⭐
- 例题:859. Kruskal算法求最小生成树
最小生成树介绍
最小生成树
有关树的定义
生成子图:生成子图是从原图中选取部分节点以及这些节点之间的边所组成的图。生成子图中的所有节点和边都必须在原图中存在。
生成树:一个连通无向图的生成子图,同时要求是树。也即在图的边集中选择 n - 1 条,将所有顶点连通。
我们定义无向连通图的 最小生成树(Minimum Spanning Tree,MST)为边权和最小的生成树。
注意:只有连通图才有生成树,而对于非连通图,只存在生成森林。
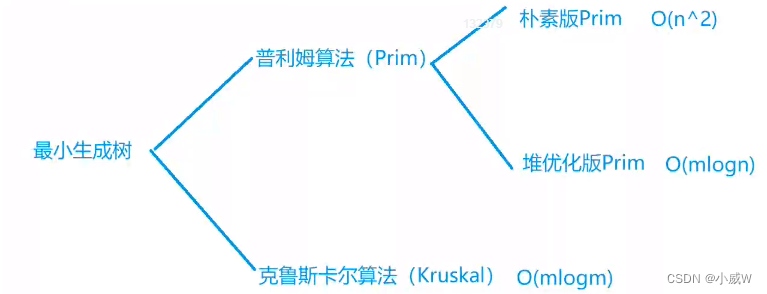
朴素Prim算法
算法思路⭐
算法流程和 Dijkstra 算法非常相似。
Dijkstra 算法是用 t 更新其它点到起点的距离,而 Prim 用 t 更新其它点到 集合 的距离。

初始时各个点到集合的距离设置为 INF
循环 n 次,每次循环找到当前没在集合(集合就是最小生成树中节点的集合)且距离集合最近的节点。
将当前最近的节点 t 加入最小生成树中,然后使用 t 更新其它所有点(1~n)到集合之间的距离。
时间复杂度是: O ( n 2 + m ) O(n^2 + m) O(n2+m)
例题:858. Prim算法求最小生成树
https://www.acwing.com/problem/content/description/860/

注意:图中可能存在重边和自环。
重边是指连接同一对顶点的多条边。在处理重边的时候,我们应当只保留权重最小的那条边,其他的边应当被忽略。
自环是指从一个顶点指向自身的边。在最小生成树中,自环是没有意义的,因为我们可以直接忽略这样的边。实际上,对于 Prim 算法,我们应当在初始化阶段,忽略这些自环,即将其赋予无穷大的权重。
另外注意图是无向图,因此在建图时应当同时更新 g [ u ] [ v ] = g [ v ] [ u ] = M a t h . m i n ( g [ u ] [ v ] , w ) ; g[u][v] = g[v][u] = Math.min(g[u][v], w); g[u][v]=g[v][u]=Math.min(g[u][v],w);
import java.util.*;public class Main {static final int INF = 0x3f3f3f3f;public static void main(String[] args){Scanner scanner = new Scanner(System.in);int n = scanner.nextInt(), m = scanner.nextInt();// 边数很多,所以使用邻接矩阵来存储int[][] g = new int[n + 1][n + 1];for (int i = 1; i <= n; ++i) {Arrays.fill(g[i], INF); // 对于自环也应该把距离设置成INF}for (int i = 0; i < m; ++i) {int u = scanner.nextInt(), v = scanner.nextInt(), w = scanner.nextInt();g[u][v] = g[v][u] = Math.min(g[u][v], w); // 是无向图,所以g[u][v] = g[v][u]都要更新}// 求最小生成树的树边权重之和int sum = prim(g);System.out.println(sum > INF / 2? "impossible": sum);}static int prim(int[][] g) {int n = g.length - 1, res = 0;boolean[] st = new boolean[n + 1]; // 存储每个点是否已经在生成树中了int[] dis = new int[n + 1]; // 存储其它点到当前最小生成树的距离Arrays.fill(dis, 0x3f3f3f3f); // 初始时距离都是 INFfor (int i = 0; i < n; ++i) {// 找到当前和集合最近且不在集合中的节点tint t = -1;for (int j = 1; j <= n; ++j) {if (!st[j] && (t == -1 || dis[t] > dis[j])) t = j;}if (i != 0 && dis[t] == INF) return INF; // 如果第一个节点没有把任何节点到最小生成树的距离变小// 将 t 加入最小生成树中去if (i != 0) res += dis[t]; // 注意判断树中的第一个节点是不会贡献边权和的st[t] = true;// 使用 t 到各个节点的距离 更新 各个节点到当前最小生成树的距离for (int j = 1; j <= n; ++j) {dis[j] = Math.min(dis[j], g[t][j]);}}return res;}
}Kruskal算法
算法思路⭐
- 先将所有边按权重从小到大排序
- 枚举每条边 a ,b , w。如果 a, b 不连通就把这条边加入集合,即加入最小生成树。

如果使用 O ( m log m ) O(m\log m) O(mlogm) 的排序算法,并且使用 O ( m α ( m , n ) ) O(m\alpha(m, n)) O(mα(m,n)) 或 O ( m log n ) O(m\log n) O(mlogn) 的并查集,就可以得到时间复杂度为 O ( m log m ) O(m\log m) O(mlogm) 的 Kruskal 算法。
例题:859. Kruskal算法求最小生成树
https://www.acwing.com/activity/content/problem/content/925/

import java.util.*;public class Main {static final int INF = 0x3f3f3f3f, N = 100005;static int[] p = new int[N];static int n;public static void main(String[] args){Scanner scanner = new Scanner(System.in);n = scanner.nextInt();int m = scanner.nextInt();// 记录所有的 m 个边int[][] edges = new int[m][3];for (int i = 0; i < m; ++i) {edges[i][0] = scanner.nextInt();edges[i][1] = scanner.nextInt();edges[i][2] = scanner.nextInt();}int res = kruskal(edges);System.out.println(res == INF? "impossible": res);}static int find(int x) {if (x != p[x]) p[x] = find(p[x]);return p[x];}static int kruskal(int[][] edges) {// 按照权重升序排序Arrays.sort(edges, (a, b) -> a[2] - b[2]);Arrays.setAll(p, e -> e); // 初始化并查集int res = 0, cnt = 0;for (int[] edge: edges) {int x = edge[0], y = edge[1];if (find(x) != find(y)) {p[find(x)] = find(y);res += edge[2];cnt++;}}if (cnt < n - 1) return INF;return res;}
}
相关文章:

【算法基础:搜索与图论】3.5 求最小生成树算法(PrimKruskal)
文章目录 最小生成树介绍朴素Prim算法算法思路⭐例题:858. Prim算法求最小生成树 Kruskal算法算法思路⭐例题:859. Kruskal算法求最小生成树 最小生成树介绍 最小生成树 有关树的定义 生成子图:生成子图是从原图中选取部分节点以及这些节点…...
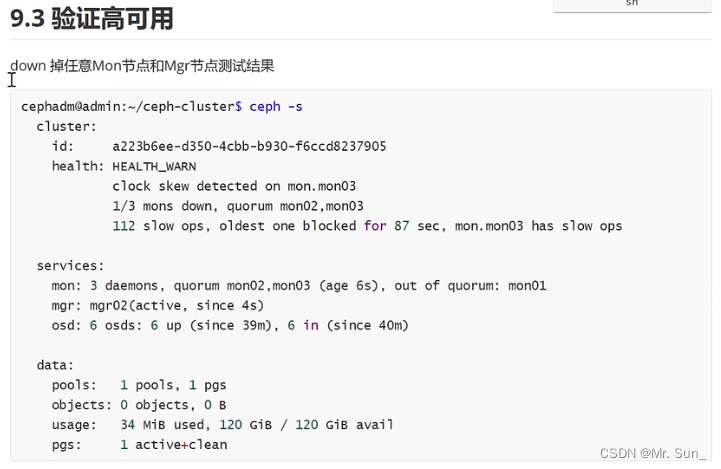
扩展Ceph集群实现高可用
...

代码随想录 DAY45
class Solution { public: int climbStairs(int n) { vector<int>dp(n1,0); dp[0]1; for(int j0;j<n;j){ for(int i1;i<2;i){ if(j>i) dp[j]dp[j-i]; } } return dp[n]; } }; 这个题还是说想清楚 这个因为有1和2 阶的情况 所以i就是从1开始遍历 然后小于等于…...
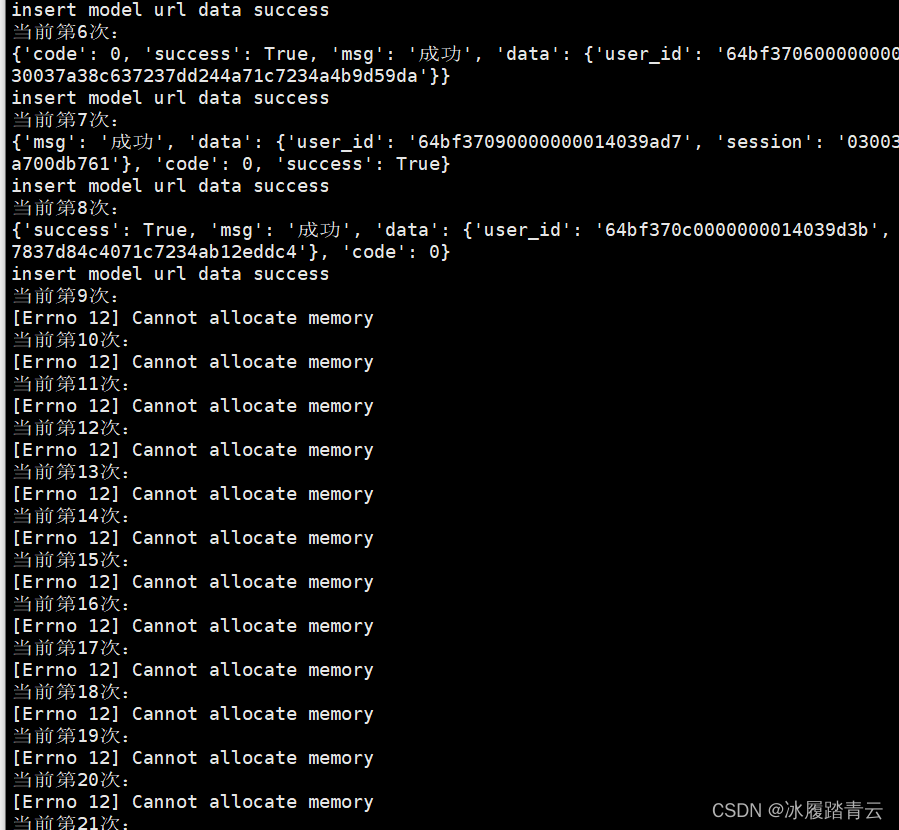
Centos报错:[Errno 12] Cannot allocate memory
执行一个脚本刚开始正常,后面就报[Errno 12] Cannot allocate memory 如果内存不足,可能需要增加交换内存。或者可能根本没有启用交换。可以通过以下方式检查您的交换: sudo swapon -s如果它为空,则表示您没有启用任何交换。添加 1GB 交换…...

手把手教你怎么写顺序表
目录 一、顺序表有什么功能? 二、实现顺序表的各个功能 1.前置准备 2.初始化顺序表 3.顺序表扩容 4.打印顺序表 5.增加顺序表成员 5.1尾增 5.2头增 6.删除顺序表中成员的内容 6.1尾删 6.2头删 7.查找成员 8.修改(替换) 9.插入(在目标位置插入成员) 10.定…...
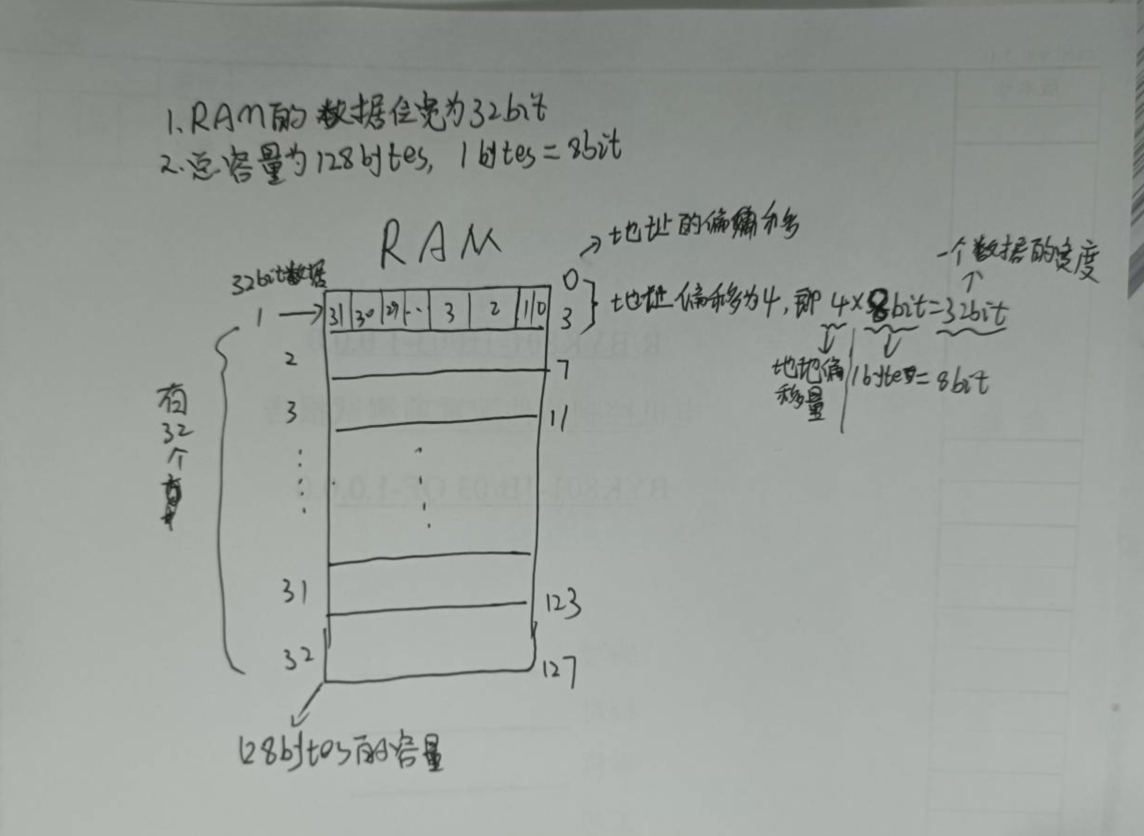
FPGA中RAM的结构理解
FPGA中RAM的结构理解 看代码的过程中对RAM的结构不是很理解,搞脑子一片浆糊,反复推算,好不容易理清了思路,记录下来,防止忘记。开辟的RAM总容量为128bytes,数据的位宽为32位(即一个单元有32bit…...

家庭用的无线洗地机到底好不好用?2023洗地机品牌排行榜前十名
无线洗地机在清洁使用的时候非常便捷,多功能于一体能够轻轻松松就拖扫完全家,不需要多余的先扫再拖,浪费时间还非常的劳累。那么有什么靠谱并且质量也有保障的无线洗地机推荐吗?为了给想要选购洗地机的小伙伴提供一些参考…...

[React]常见Hook实现之useUpdateEffect
useUpdateEffect是一个自定义的React Hook,用于在组件更新时执行副作用。它的实现原理如下: useEffect和useLayoutEffect:useUpdateEffect内部使用useEffect或useLayoutEffect来注册副作用函数。这两个Hook函数都接受一个回调函数和依赖项数…...

为什么视频画质会变差,如何提升视频画质清晰度。
在数字时代,视频已经成为我们生活中不可或缺的一部分。然而,随着视频的传输和处理过程中的多次压缩,画质损失逐渐凸显,影响了我们对影像的真实感受。为了让视频画质更加清晰、逼真,我们需要采取一些措施来保护和修复视…...

【uni-app2.0】实现登录页记住密码功能
使用uni-app的uni.setStorageSync()和uni.getStorageSync()方法来存储和读取密码 在登录页中添加一个记住密码的u-checkbox选项,并在data里面添加一个rememberPwd的布尔值,在每次点击记住密码change的时候来记录用户的选择 <u-checkbox-group place…...
IDEA live templates
surround 在SQL的xml里 可以修改变量 官方文档 CDATA not null <if test"$SELECTION$ ! null and $SELECTION$ ! "> and $VAR1$ #{$SELECTION$} </if>not null like mysql <if test"$SELECTION$ ! null and $SELECTION$ ! "> and…...

电子鼻毕业论文
面向压埋探测的人体代谢气体识别方法的研究与应用 实现对非目标气体的检测 数据预处理 (1a)标准化 将采集到的数据先进行变换,统一数量级。其中,xij为第j个传感器的第i个采样值;xj为第 j 个气体传感器的所有采样值&…...

8 | 爬虫解析利器 PyQuery 的使用
文章目录 爬虫解析利器 PyQuery 的使用简介安装基本用法初始化查找元素遍历元素修改元素练习题练习题 1练习题 2答案练习题 1练习题 2总结爬虫解析利器 PyQuery 的使用 简介 PyQuery 是一个 Python 的库,它是 jQuery 的 Python 实现。PyQuery 可以让开发者使用类似于 jQuery…...

2023年 React 最佳学习路线
CSS CSS JavaScript JavaScript TypeScript 目前没有找到比其他文档好很多的文档地址 可以先看官网 React 新版 React 官方文档无敌 React React-router-dom V5 V6 Webpack webpack Antd antd...

使用 ChatGPT 进行研究的先进技术
在这篇文章中,您将探索改进您研究的先进技术。尤其, 分析和解释研究数据进行文献综述并找出研究差距废话不多说直接开始吧!!! 分析和解释研究数据 一家小企业主希望分析客户满意度数据以改善客户服务。他们使用包含 10…...

Java-API简析_java.net.Proxy类(基于 Latest JDK)(浅析源码)
【版权声明】未经博主同意,谢绝转载!(请尊重原创,博主保留追究权) https://blog.csdn.net/m0_69908381/article/details/131881661 出自【进步*于辰的博客】 因为我发现目前,我对Java-API的学习意识比较薄弱…...

磁盘问题和解决: fsck,gdisk,fdisk等
错误: Resize inode not valid 对于gpt分区的硬盘一般fsck只能检查分区, 不能用于检查整个硬盘, 但是如果对硬盘设备运行时遇到这样的错误 $ sudo fsck -n /dev/sdc fsck from util-linux 2.37.2 e2fsck 1.46.5 (30-Dec-2021) GW1.5T was not cleanly unmounted, check force…...

基于深度学习的高精度六类海船检测识别系统(PyTorch+Pyside6+YOLOv5模型)
摘要:基于深度学习的高精度六类海船检测识别系统可用于日常生活中检测与定位海船目标(散装货船(bulk cargo carrier)、集装箱船(container ship)、渔船(fishing boat)、普通货船&…...
【React Native】学习记录(一)——环境搭建
Expo是一套工具,库和服务,可让您通过编写JavaScript来构建原生iOS和Android应用程序。 一开始学习的时候直接使用的是expo。 npx create-expo-app my-appcd my-appnpm run start接下来需要搭建安卓和IOS端(为此特意换成了苹果电脑)…...
Java 设计模式 - 简单工厂模式 - 创建对象的简便之道
简单工厂模式是一种创建型设计模式,它提供了一种简单的方式来创建对象,而无需暴露对象创建的逻辑。在本篇博客中,我们将深入了解简单工厂模式的概念、实现方式以及如何在Java中使用它来创建对象。 为什么使用简单工厂模式? 在软…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...
