7.25训练总结
考场错误:
A题其实并不简单,但是先想了一个方法后,就交了,wa了后一直卡住,策略不当,到最后后期写C的时候也犯了一些低级的错误,这点需要注意。
之后顺利的把BCDHI写完后,又完成了A的改正补充,最后又把G完成了,最终做出了7个题,但罚时最多,应该注意正确率
Gym - 100738E
启发式合并的模板题,其实看到25次的限制,就应该想到应该和log有关,结合最小生成树的Kruskal的算法,把边权排序一个一个做合并就可以了,注意每次选择sz小的往sz大的上面合并就好了
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=2e5+5;
int n,m;
struct edge
{int x,y,z;
}e[maxn<<1];
int fa[maxn],bus[maxn];
vector <int> driver[maxn];
bool cmp(edge x,edge y)
{return x.z<y.z;
}
int find(int x)
{if(x==fa[x]) return x;return fa[x]=find(fa[x]);
}
vector <int> G[maxn];
int gs;
ll res;
void print(int u,int ff)
{for(int to:G[u]){if(to==ff) continue;print(to,u);if(driver[bus[to]].size()>driver[bus[u]].size())swap(bus[u],bus[to]);for(int v:driver[bus[to]]){driver[bus[u]].push_back(v);printf("Move %d %d %d\n",v,bus[to],bus[u]);}}if(ff) printf("Drive %d %d %d\n",bus[u],u,ff);
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=m;i++) scanf("%d%d%d",&e[i].x,&e[i].y,&e[i].z);for(int i=1;i<=n;i++) fa[i]=i,bus[i]=i,driver[i].push_back(i);sort(e+1,e+m+1,cmp);for(int i=1;i<=m;i++){int fx=find(e[i].x),fy=find(e[i].y);if(fx==fy) continue;fa[fx]=fy;res+=e[i].z;G[e[i].x].push_back(e[i].y);G[e[i].y].push_back(e[i].x);gs++; if(gs==n-1) break;}printf("%lld\n",res);for(int i=1;i<=n;i++) fa[i]=i;print(1,0);printf("Done\n");return 0;
}
Gym - 100738F
后缀数组的裸题,可以使用后缀数组后
然后把询问离线,按照长度依次处理,对于同一个长度,二分配合树状数组计算即可
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
int n;
char s[maxn];
int sa[maxn],rk[maxn],cnt[maxn],fz[maxn];
int oldrk[maxn],id[maxn];
bool cmp(int x,int y,int w)
{return oldrk[x]==oldrk[y] && oldrk[x+w]==oldrk[y+w];
}
void SA()
{int m=233;for(int i=0;i<=m;i++) cnt[i]=0;for(int i=1;i<=n;i++) cnt[rk[i]=s[i]]++;for(int i=1;i<=m;i++) cnt[i]+=cnt[i-1];for(int i=n;i>=1;i--) sa[cnt[rk[i]]--]=i;int i,p;for(int w=1;;w<<=1,m=p){for(p=0,i=n;i>n-w;i--) id[++p]=i;for(i=1;i<=n;i++) if(sa[i]>w) id[++p]=sa[i]-w;for(i=0;i<=m;i++) cnt[i]=0;for(i=1;i<=n;i++) cnt[fz[i]=rk[id[i]]]++;for(i=1;i<=m;i++) cnt[i]+=cnt[i-1];for(i=n;i>=1;i--) sa[cnt[fz[i]]--]=id[i];for(i=1;i<=n;i++) oldrk[i]=rk[i];for(p=0,i=1;i<=n;i++) rk[sa[i]]=cmp(sa[i],sa[i-1],w)?p:++p;if(p==n){for(i=1;i<=n;i++) sa[rk[i]]=i;break;}}
}
struct Query
{int id,l,k;
}q[maxn];
int Q;
bool ccmp(Query x,Query y)
{return x.l<y.l;
}
int c[maxn];
int lowbit(int x)
{return x&-x;
}
void add(int pos,int x)
{while(pos<=n){c[pos]+=x;pos+=lowbit(pos);}
}
int ask(int pos)
{int res=0;while(pos){res+=c[pos];pos-=lowbit(pos);}return res;
}
int res[maxn];
int main()
{scanf("%s",s+1);n=strlen(s+1);SA();scanf("%d",&Q);for(int i=1;i<=Q;i++){scanf("%d%d",&q[i].l,&q[i].k);q[i].id=i;} sort(q+1,q+Q+1,ccmp);int now=1;for(int i=1;i<=Q;i++){while(now<q[i].l){add(rk[n-now+1],1);now++;}int l=1,r=n,ans=0;while(l<=r){int mid=l+r>>1;if(mid-ask(mid)>=q[i].k) ans=mid,r=mid-1;else l=mid+1;}res[q[i].id]=sa[ans];}for(int i=1;i<=Q;i++) printf("%d\n",res[i]);return 0;
}
相关文章:

7.25训练总结
考场错误: A题其实并不简单,但是先想了一个方法后,就交了,wa了后一直卡住,策略不当,到最后后期写C的时候也犯了一些低级的错误,这点需要注意。 之后顺利的把BCDHI写完后,又完成了A的…...
java注解@FeignClient修饰的类路径不在spring boot入口类所在的包下,有哪几种处理方式?
一、注解EnableFeignClients 修饰在spring boot入口类,使得openfeign的FeignClient注解生效。 我们进一步看看注解EnableFeignClients的使用方式。 String[] basePackages() default {};Class<?>[] basePackageClasses() default {};Class<?>[] clie…...

神经网络随记-参数矩阵、剪枝、模型压缩、大小匹配、、
神经网络的参数矩阵 在神经网络中,参数矩阵是模型学习的关键部分,它包含了神经网络的权重和偏置项。下面是神经网络中常见的参数矩阵: 权重矩阵(Weight Matrix):权重矩阵用于线性变换操作,将输…...

4、Kubernetes 集群 YAML 文件详解
目录 一、YAML 概述 二、YAML 基本语法 三、YAML 数据结构 四、k8s资源清单描述方法 五、YAML 快速编写 1、使用 kubectl create 命令 2、使用 kubectl get 命令导出 yaml 文件 一、YAML 概述 k8s 集群中对资源管理和资源对象编排部署都可以通过声明YAML文件来解决&…...
)
leetcode93. 复原 IP 地址(java)
复原 IP 地址 leetcode93. 复原 IP 地址回溯算法代码演示 回溯算法 leetcode93. 复原 IP 地址 有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 ‘.’ 分隔。 例如:“0.1.2…...

极光Java 版本服务器端实现别名消息推送
文章目录 引言I 概述1.1 依赖包1.2 极光证书环境参数1.3 构建推送对象II 推送内容2.1 配置推送内容2.2 获取通知消息内容2.3 配置IOS通知内容2.4 配置Android通知内容2.5 发起推送2.6 分批推送2.7 初始化密钥2.8 配置密钥引言 REST API 文档:https://docs.jiguang.cn/jpush/se…...

【Lua学习笔记】Lua进阶——Table(4)继承,封装,多态
文章目录 封装继承多态 封装 // 定义基类 Object {}//由于表的特性,该句就相当于定义基类变量 Object.id 1//该句相当于定义方法,Object可以视为定义的对象,Test可以视为方法名 //我们知道Object是一个表,但是抽象地看ÿ…...
Linux中常用的指令
ls ls [选项] [目录或文件] 功能:对于目录,列出该目录下所有的子目录和文件;对于文件,列出该文件的文件名和其他属性 常用选项: -a:列出目录下的所有文件,包括以.开头的隐藏文件 -l:列出文件的详细信息。…...
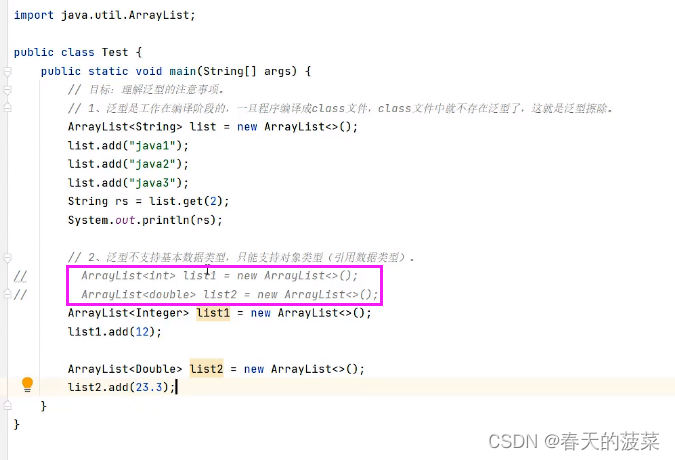
【java】【面对对象高级4】内部类、枚举、泛型
目录 1、内部类 1.1 成员内部类【了解】 1.1.1 定义 1.1.2 扩展变量 1.2 静态内部类【了解】 1.2.1 定义 1.2.2 扩展变量 1.3 局部内部类【了解】 1.4 匿名内部类【重点】 1.4.1 定义 1.4.1.1 常规写法 1.4.1.2 匿名内部类改造 1.4.2 匿名内部类的常见使用场景 1.4.2…...
)
Python的用处到底是什么?(三)
11. 数据库操作:Python的库,如sqlite3和SQLAlchemy,可以连接和操作各种类型的数据库。 Python提供了一些库和工具,如sqlite3和SQLAlchemy,用于连接和操作各种类型的数据库。以下是关于这两个库的详细解释:…...
【Nodejs】Express基本使用
Express 中文网 基于 Node.js 平台,快速、开放、极简的 web 开发框架。 1.Express的安装方式 Express的安装可直接使用npm包管理器上的项目,在安装npm之前可先安装淘宝镜像: npm install -g cnpm --registryhttps://registry.npmmirror.com/…...

k8s集群安装v1.20.9
参考网上资料并将异常问题解决,经测试可正常安装集群。 1.我的环境准备 本人使用vmware pro 17新建三个centos7虚拟机,每个2cpu,20GB磁盘存储,内存2GB,其中主节点的内存3GB,可使用外网. 2.所有节点安装D…...

Staples Drop Ship EDI 需求分析
Staples 是一家美国零售公司,总部位于马萨诸塞州弗拉明汉,主要提供支持工作和学习的产品和服务。该公司于 1986 年在马萨诸塞州布莱顿开设了第一家门店。到 1996 年,该公司已跻身《财富》世界 500 强,后来又收购了办公用品公司 Qu…...

模型调参及优化
调参 调权重参数,偏置参数 训练数据集用来训练参数w,b 调超参数 验证数据集用来选择超参数学习率lr,隐藏层大小等 如何调参 当泛化误差和训练误差都没有降下去说明欠拟合;当训练误差降下去,但泛化误差出现上升形式&…...

多数据源数据转换和同步的ETL工具推荐
有许多支持多数据源数据转换和同步的ETL工具可供选择。以下是一些常见的ETL工具和它们支持多数据源数据转换和同步的特点: Apache NiFi:Apache NiFi是一个开源的ETL工具,支持多种数据源的连接,包括文件系统、数据库、消息队列、网…...

配置 gitlab https 访问
文章目录 1. 备份2. 生成SSL证书3. 配置文件4. 重启5. 访问 1. 备份 docker exec -ti gitlab-ce gitlab-rake gitlab:backup:create2. 生成SSL证书 yum install openssl openssl-devel -y mkdir /data/gitlab/config/ssl ; cd /data/gitlab/config/ssl### 生成证书 openssl…...
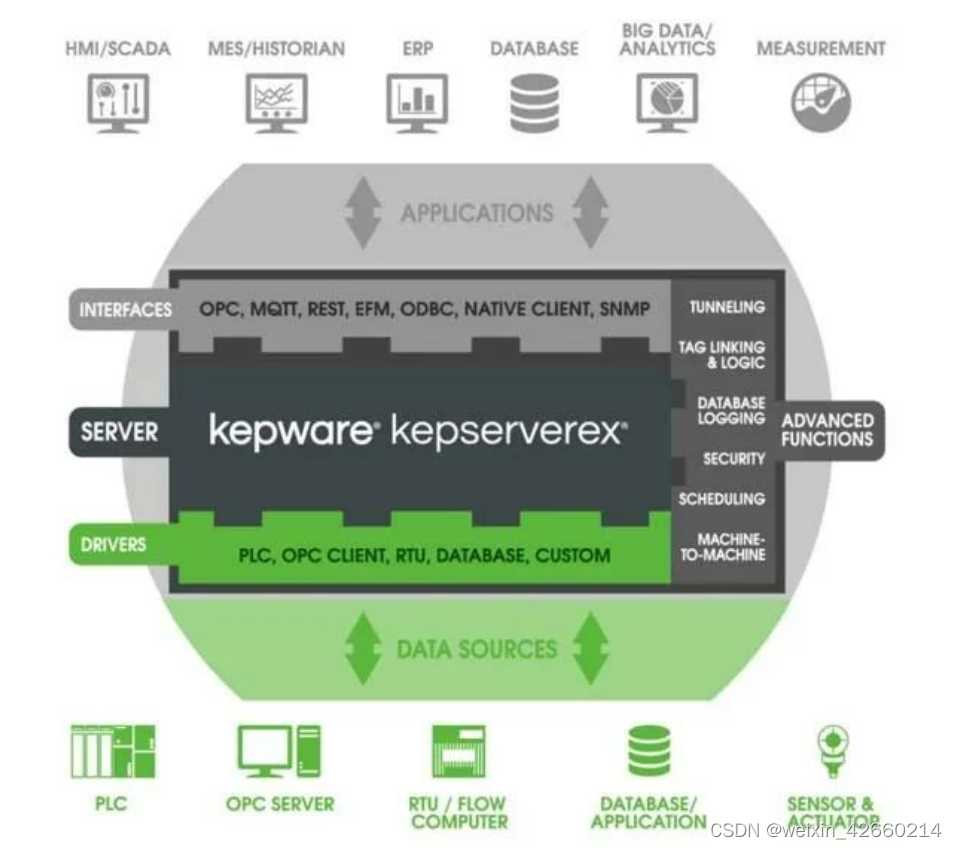
Kepware Modbus驱动简介
1. Modbus驱动能够解决什么问题? 它是Modbus设备驱动的集合,为用户提供一种方便快捷的Modbus设备数采解决方案。 只需要通过简单的配置就可以将常见的例如Modbus TCP/IP Ethernet、RTU Serial 和 ASCII Serial等协议设备无缝连接到 HMI/SCADA、MES/His…...
从零开始学习CTF——CTF是什么
引言: 从2019年10月开始接触CTF,学习了sql注入、文件包含等web知识点,但都是只知道知识点却实用不上,后来在刷CTF题才发现知识点的使用方法,知道在哪里使用,哪里容易出漏洞,可是在挖src漏洞中还…...

为Android构建现代应用——主体结构
创建Screents和ViewModels 在前面的章节中,我们已经分析了OrderNow项目的理论概念和我们将赋予的组织。 在本章中,我们将开始实现初始结构和模板,这将联接每一个应用程序的部分。 首先将添加以下带有各自视图模型的主屏幕: •…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

