【数据挖掘】PCA/LDA/ICA:A成分分析算法比较
一、说明
如果您想了解更多关于PCA和ZCA之间的区别,请查看我之前基于numpy的帖子:
PCA 美白与 ZCA 美白:2D 视觉效果
白化数据的过程包括转换,使得转换后的数据具有单位矩阵作为...
towardsdatascience.com
二、各类降维模型概念
2.1 PCA : 主成分分析
- PCA是一种无监督线性降维技术,旨在找到一组新的正交变量,以捕获数据中最重要的可变性来源。
- 它广泛用于特征提取和数据压缩,可用于探索性数据分析或作为机器学习算法的预处理步骤。
- 生成的分量按其解释的方差量进行排名,可用于可视化和解释数据,以及用于聚类或分类任务。
2.2 LDA : 线性判别分析
- LDA 是一种受监督的线性降维技术,旨在找到一组新的变量,以最大化类之间的分离,同时最小化每个类内的变化。
- 它广泛用于特征提取和分类,可用于降低数据的维数,同时保留类之间的判别信息。
- 生成的组件按其判别能力进行排名,可用于可视化和解释数据,以及用于分类或回归任务。
2.3 ICA : 独立成分分析
- ICA是一种无监督线性降维技术,旨在找到一组统计上独立且非高斯的新变量。
- 它广泛用于信号处理和源分离,并可用于提取数据中无法通过其他技术访问的潜在可变性源。
- 生成的组件按其独立性进行排名,可用于可视化和解释数据,以及用于聚类或分类任务。
三、鸢尾花数据集上的结果
让我们使用 sklearn 比较他们在著名的鸢尾花数据集上的结果。首先,让我们在 4 个数值特征中的每一个上使用配对图绘制鸢尾花数据集,并将颜色作为分类特征:
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris# Load the iris dataset
iris = load_iris()
data = iris.data
target = iris.target
target_names = iris.target_names# Convert the iris dataset into a pandas DataFrame
iris_df = sns.load_dataset('iris')
iris_df['target'] = target# Generate the pairplot∑
sns.pairplot(data=iris_df, hue='target', palette=['navy', 'turquoise', 'darkorange'], markers=['o', 's', 'D'],plot_kws=dict(s=25, alpha=0.8, edgecolor='none'), diag_kws=dict(alpha=0.8, edgecolor='none'))# Set the title and adjust plot spacing
plt.suptitle('Iris Pairplot')
plt.subplots_adjust(top=0.92)plt.show()
图片来源:虹膜数据集对图
现在,我们可以计算每个变换并绘制结果。请注意,我们只使用 2 个组件,因为 LDA 最多需要 (N-1) 个组件,其中 N 是类别的数量(这里等于 3,因为有 3 种类型的鸢尾花)。
from sklearn.datasets import load_iris
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA, FastICA
import matplotlib.pyplot as plt# Load the Iris dataset
iris = load_iris()
X = iris.data
y = iris.target
target_names = iris.target_names# Standardize the data
scaler = StandardScaler()
X_std = scaler.fit_transform(X)# Apply LDA with 2 components
lda = LinearDiscriminantAnalysis(n_components=2)
X_lda = lda.fit_transform(X_std, y)# Apply PCA with 2 components
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_std)# Apply ICA with 2 components
ica = FastICA(n_components=2)
X_ica = ica.fit_transform(X_std)# Plot the results
plt.figure(figsize=(15, 5))plt.subplot(1, 3, 1)
for target, color in zip(range(len(target_names)), ['navy', 'turquoise', 'darkorange']):plt.scatter(X_lda[y == target, 0], X_lda[y == target, 1], color=color, alpha=.8, lw=2,label=target_names[target])
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('LDA')
plt.xlabel('LD1')
plt.ylabel('LD2')plt.subplot(1, 3, 2)
for target, color in zip(range(len(target_names)), ['navy', 'turquoise', 'darkorange']):plt.scatter(X_pca[y == target, 0], X_pca[y == target, 1], color=color, alpha=.8, lw=2,label=target_names[target])
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('PCA')
plt.xlabel('PC1')
plt.ylabel('PC2')plt.subplot(1, 3, 3)
for target, color in zip(range(len(target_names)), ['navy', 'turquoise', 'darkorange']):plt.scatter(X_ica[y == target, 0], X_ica[y == target, 1], color=color, alpha=.8, lw=2,label=target_names[target])
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('ICA')
plt.xlabel('IC1')
plt.ylabel('IC2')plt.show()This code loads the Iris dataset, applies LDA, PCA, and ICA with 2 components each, and then plots the results using different colors for each class.
请注意,在应用 PCA、ICA 或 LDA 之前标准化数据通常是一种很好的做法。标准化很重要,因为这些技术对输入要素的比例很敏感。标准化数据可确保每个要素的均值为 0,标准差为 1,这会将所有要素置于同一尺度上,并避免一个要素凌驾于其他要素之上。
由于LDA是一种监督降维技术,因此它将类标签作为输入。相比之下,PCA和ICA是无监督技术,这意味着它们只使用输入数据,而不考虑类标签。
LDA 的结果可以解释为将数据投影到最大化类分离的空间上,而 PCA 和 ICA 的结果可以解释为将数据投影到空间上,该空间分别捕获最重要的可变性或独立性来源。

图片来源:虹膜数据集上LDA,PCA和ICA的比较
请注意,ICA仍然显示类别之间的分离,尽管不是其目的:这是因为类别已经在输入数据集中进行了相当排序。
让我们把LDA放在一边,专注于PCA和ICA之间的差异 - 因为LDA是一种监督技术,专注于分离类别并强制实施最大的组件,而PCA和ICA专注于创建一个与输入矩阵形状相同的新矩阵。
让我们看看 PCA 和 ICA 的 4 个组件的输出:


左:PCA的对图/右:ICA的对图(图片由作者提供)
让我们也比较每个转换数据的相关矩阵:请注意,这两种方法都会导致不相关的向量(换句话说,转换后的数据特征是正交的)。这是因为它是PCA算法中的一个约束 - 每个新向量必须与以前的向量正交 - 并且是ICA算法的结果 - 这意味着原始数据集是已经混合在一起的独立信号,必须重建。


左:ICA的相关热图/右:PCA的相关热图(图片由作者提供)
所以PCA和ICA似乎给出了具有相似性质的结果:这是因为以下2个原因:
- 独立性在两种算法中都“编码”
- 鸢尾花数据集表现出分离良好的类
这就是为什么我们需要另一个更适合ICA的例子。
四、另一个例子:
让我们看另一个例子:我们首先生成一个合成数据集,其中包含两个独立的源,一个正弦波和一个方波,它们作为线性组合混合在一起以创建混合信号。
实际的、真实的、独立的信号如下:

它们混合在一起,作为 2 个线性组合:

让我们看看PCA和ICA在这个新数据集上的表现:
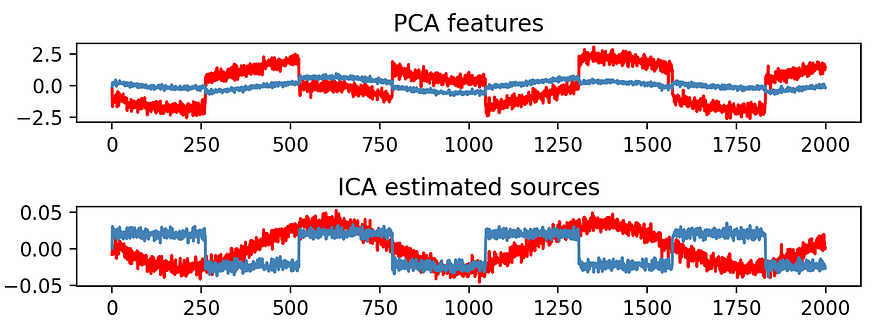
注意PCA如何创建一个新组件,该组件表现出很大的方差,作为输入的线性组合,但这绝对与原始数据不匹配:这确实不是PCA的目的。
相反,ICA在恢复原始数据集方面表现非常好,与方差组成无关。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import FastICA# Generate a synthetic dataset with two independent sources
np.random.seed(0)
n_samples = 2000
time = np.linspace(0, 8, n_samples)s1 = np.sin(2 * time) # Source 1: sine wave
s2 = np.sign(np.sin(3 * time)) # Source 2: square waveS = np.c_[s1, s2]
S += 0.2 * np.random.normal(size=S.shape) # Add noise to the sources
S /= S.std(axis=0) # Standardize the sources# Mix the sources together to create a mixed signal
A = np.array([[0.5, 0.5], [0.2, 0.8]]) # Mixing matrix
X = np.dot(S, A.T) # Mixed signal# Standardize the data
X = (X - np.mean(X, axis=0)) / np.std(X, axis=0)# Use PCA to reduce the dimensionality of the data
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)# Use ICA to separate the sources from the mixed signal
ica = FastICA(n_components=2)
X_ica = ica.fit_transform(X) # Estimated sources# Plot the results
plt.figure()models = [X, S, X_pca, X_ica]
names = ['Observations (mixed signal)','True Sources','PCA features', 'ICA estimated sources']
colors = ['red', 'steelblue']for ii, (model, name) in enumerate(zip(models, names), 1):plt.subplot(4, 1, ii)plt.title(name)for sig, color in zip(model.T, colors):plt.plot(sig, color=color)plt.tight_layout()
plt.show()五、结论
PCA、LDA 和 ICA 算法可能看起来像是彼此的自定义版本,但它们实际上没有相同的目的。总结一下:
- PCA旨在创建保持输入最大方差的新组件
- LDA 旨在创建基于分类特征分隔集群的新组件
- ICA 旨在检索在输入数据集中以线性组合混合在一起的原始要素
希望您更好地了解这些算法之间的差异,并能够在将来快速识别您需要的算法。
相关文章:

【数据挖掘】PCA/LDA/ICA:A成分分析算法比较
一、说明 在深入研究和比较算法之前,让我们独立回顾一下它们。请注意,本文的目的不是深入解释每种算法,而是比较它们的目标和结果。 如果您想了解更多关于PCA和ZCA之间的区别,请查看我之前基于numpy的帖子: PCA 美白与…...

微服务模式:业务服务模式
无论是单体应用还是微服务,构建企业应用的业务逻辑/服务在更多方面上都有相似之处而不是差异。在两种方法中,都包含服务、实体、仓库等类。然而,也会发现一些明显的区别。在本文中,我将试图以概念性的方式强调这些区别,…...

idea中创建请求基本操作
文章目录 说明效果创建GET请求没有参数带有参数带有环境变量带有动态参数 说明 首先通过###三个井号键来分开每个请求体,然后请求url和header参数是紧紧挨着的,请求参数不管是POST的body传参还是GET的parameter传参,都是要换行的,…...

springboot整合log4j2
1.排除springboot本身日志 2.添加log4j2 maven没有父项目 就必须指定version!! 3.配置application.yml文件 打印sql级别为debug 4.配置log4j2.xmllogging.configclasspath:log4j2.xml logging.level.com.zhkj.shoppingdebug #mybatis-plus.mapper-locations classpath*:/mapp…...
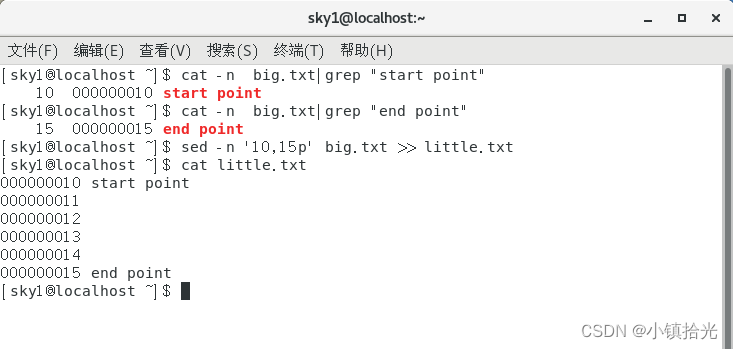
Linux输出内容到指定文件
1. 记录终端输出至文本文件 1.1 解决方案1:利用>和>>命令 区别: > 是把输出转向到指定的文件。注意:如文件已存在的话会重新写入,文件原内容不会保留。 >> 是把输出附加到文件的后面,文件原内容会…...

mysql主从同步怎么跳过错误
今天介绍两种mysql主从同步跳过错误的方法: 一、两种方法介绍 1、跳过指定数量的事务: mysql>slave stop; mysql>SET GLOBAL SQL_SLAVE_SKIP_COUNTER 1 #跳过一个事务 mysql>slave start2、修改mysql的配置文件,通过slav…...

【论文阅读】DEPIMPACT:反向传播系统依赖对攻击调查的影响(USENIX-2022)
Fang P, Gao P, Liu C, et al. Back-Propagating System Dependency Impact for Attack Investigation[C]//31st USENIX Security Symposium (USENIX Security 22). 2022: 2461-2478. 攻击调查、关键边、入口点 开源:GitHub - usenixsub/DepImpact 目录 1. 摘要2. 引…...

Nginx 功能及配置详解
一、Nginx概述 Nginx是一款高性能的HTTP和反向代理服务器,也是一款IMAP/POP3/SMTP代理服务器。Nginx被广泛应用于服务端的Web开发,主要用于提供高效、稳定的网页访问服务。Nginx的主要特点包括:高并发连接处理能力、稳定性高、配置灵活和功能…...

CSS 瀑布流效果效果
示例 <!DOCTYPE html> <html lang="cn"><head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-scale=1.0"><title>瀑布流效果</title><style>…...
Python 进阶(一):PyCharm 下载、安装和使用
❤️ 博客主页:水滴技术 🌸 订阅专栏:Python 入门核心技术 🚀 支持水滴:点赞👍 收藏⭐ 留言💬 文章目录 一、下载 PyCharm二、安装 PyCharm三、创建项目四、界面汉化五、实用技巧5.1、使用快捷…...

微信小程序使用ECharts的示例详解
目录 安装 ECharts 组件使用 ECharts 组件图表延迟加载 echarts-for-weixin 是 ECharts 官方维护的一个开源项目,提供了一个微信小程序组件(Component),我们可以通过这个组件在微信小程序中使用 ECharts 绘制图表。 echarts-fo…...
可添加logo)
微信小程序生成二维码(weapp-qrcode)可添加logo
插件 npm 地址:https://www.npmjs.com/package/weapp-qrcode 插件 GitHub 地址:https://github.com/yingye/weapp-qrcode/tree/master 一、引入 1、根据 GitHub 指引将 weapp-qrcode 放到本地 uitl 文件夹下; 2、创建 canvas <canvas c…...

【云原生】Docker容器资源限制(CPU/内存/磁盘)
目录 编辑 1.限制容器对内存的使用 2.限制容器对CPU的使用 3.block IO权重 4.实现容器的底层技术 1.cgroup 1.查看容器的ID 2.在文件中查找 2.namespace 1.Mount 2.UTS 3.IPC 4.PID 5.Network 6.User 1.限制容器对内存的使用 ⼀个 docker host 上会运⾏若⼲容…...
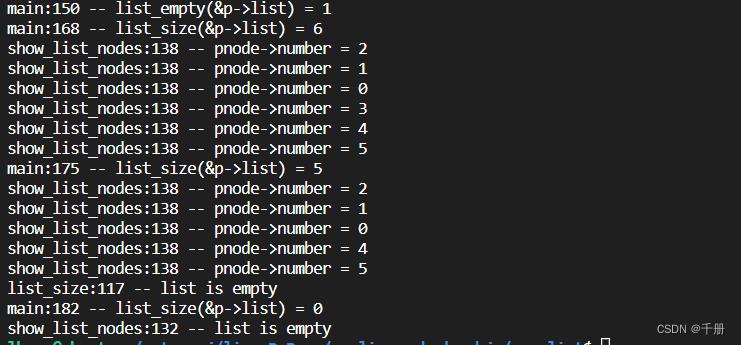
内核链表在用户程序中的移植和使用
基础知识 struct list_head {struct list_head *next, *prev; }; 初始化: #define LIST_HEAD_INIT(name) { (name)->next (name); (name)->prev (name);} 相比于下面这样初始化,前面初始化的好处是,处理链表的时候,不…...

使用C#基于ComPDFKit SDK快速构建PDF阅读器
在当今世界,Windows 应用程序对我们的工作至关重要。随着处理 PDF 文档的需求不断增加,将 ComPDFKit PDF 查看和编辑功能集成到您的 Windows 应用程序或系统中,可以极大地为您的用户带来美妙的体验。 在本博客中,我们将首先探索集…...

el-tabel导出excel表格
1、安装插件 npm install file-saver --save npm install xlsx --save 2、引入插件 import FileSaver from "file-saver"; import * as XLSX from xlsx; 3、在tabel中添加ref属性和导出方法 4、添加方法 exportExcel (excelName) {try {const $e this.$refs[repo…...
双击start.bat文件闪退,运行报错“unable to access jarfile”
问题:电脑运行“start.bat”文件,无反应,闪退,管理员身份运行报错“unable to access jarfile” 解决思路: 1、由于该项目运行需要jdk环境,检查jdk版本需要是1.8.0_251版本 通过在 cmd 命令行输入java -v…...

大数据Flink(五十一):Flink的引入和Flink的简介
文章目录 Flink的引入和Flink的简介 一、Flink的引入 1、第1代——Hadoop MapReduce...

c语言的数据类型 -- 与GPT对话
1 c语言的数据类型 在C语言中,数据类型用于定义变量的类型和存储数据的方式。C语言支持多种数据类型,包括基本数据类型和派生数据类型。以下是C语言中常见的数据类型: 基本数据类型(Primary Data Types): int: 整数类型,通常表示带符号的整数。char: 字符类型,用于存储…...
Truffle 进行智能合约测试
其他依赖 node.js、 由于是利用npm进行,所以先设置国内镜像源。去网上搜 1.安装truffle npm install truffle -gtruffle --version 安装完其他项目依赖,能够产生一下效果 2.项目创建 创建test文件夹 mkdir test进入test cd test初始化项目 truffle …...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...
