simulink与遗传算法结合求解TSP问题
前言:刚开始入门学习simulink,了解了基本的模块功能后想尝试从自己熟悉的领域入手,自己出题使用simulink搭建模型。选择的是TSP问题的遗传算法,考虑如何用simulink建模思想来实现一个简单TSP问题的遗传算法。
TSP问题描述
一个配送中心,8个需求点,各个需求点间的距离以及需求点离配送中心的距离已知,车辆从配送中心出发遍历每个需求点有且仅有一次,最后又回到配送中心,求最短的配送路线。

处理输入数据
万事开头难,从输入参数的配置开始吧。
主要是处理各个节点(配送中心+需求点)间的距离矩阵。
第一种方案:直接在查表模块中填写数据


第二种方案:也可以将excel表格中记录距离矩阵的数据导入.m文件,最后生成可以供查表模块使用的.mat文件数据
参考文章:Simulink仿真中将工作空间中的数据变量保存成.mat文件
https://blog.csdn.net/jk_101/article/details/120019475

本人采用的是第二种方案实现输入距离矩阵的处理。
用.m文件存储数据
clc;
clear;%% 处理各节点间的路线距离输入数据
%读取excel中,第一个sheet,B2-J10之间的内容
distance_data_file = 'distance_data.xlsx';
curr_path = matlab.desktop.editor.getActiveFilename; % 获取当前.m脚本的工作路径
[pathstr, name, suffix] = fileparts(curr_path); % 获取文件的上层父节点路径、文件名称、文件后缀
full_distance_path = fullfile(pathstr, distance_data_file); % 拼接文件路径
distance_cube = xlsread(full_distance_path, 1, 'B2:J10');
save('distance_cube.mat', 'distance_cube');
9个节点(包括配送中心节点0)的距离数据存储在一个9*9的矩阵中,命名为distance_cube,使用save(‘distance_cube.mat’, ‘distance_cube’); 这条语句将从excel读取的距离矩阵存入distance_cube.mat供Simulink模型使用。
生成单条染色体
染色体编码方式采用整数编码方式,每一条染色体代表一种可行解,染色体中的每个基因位数字代表一个节点。
首先思考一条染色体在simulink中应该怎么表示?
假设:染色体A:0 1 2 3 4 5 6 7 8 0,可以直接使用constant模块表示

也可以使用Constant模块随机产生1-8的一维数组。
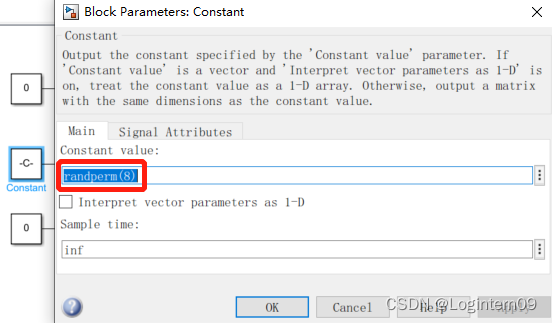
再使用Mux模块合并输入数据,得到一个以配送中心编号0开头和结尾的序列,这个序列就表示问题的一个可行解。

计算可行解的适应度函数
假设可行解为[0,1,2,3,4,5,6,7,8,0]
从基本单元“基因”开始处理

按照上面两个基因(节点)查表确认距离的思想,将基因使用Constant模块重组为一条染色体,计算单条染色体的适应度函数(总配送路线长度),备注:本博客提到的适应度函数不是真正意义上遗传算法要求的总运输距离的倒数,Simulink建模计算的染色体的适应度就是指代的总运输距离(车辆从配送中心出发依次经过8个需求点再返回配送中心的总路线长度)。


确定种群结构
假设染色体种群规模为10,采用Constant产生1-8个需求节点的随机序列,使用自定义的模块封装车辆从配送中心出发依次经过8个需求节点最后返回配送中心的过程。
自定义封装好的模块如下:
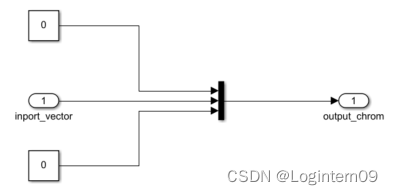
使用Mux模块合并输入数据(即10条染色体)组成形式上的种群,将输出结果采用To File模块存入initpopout.mat。
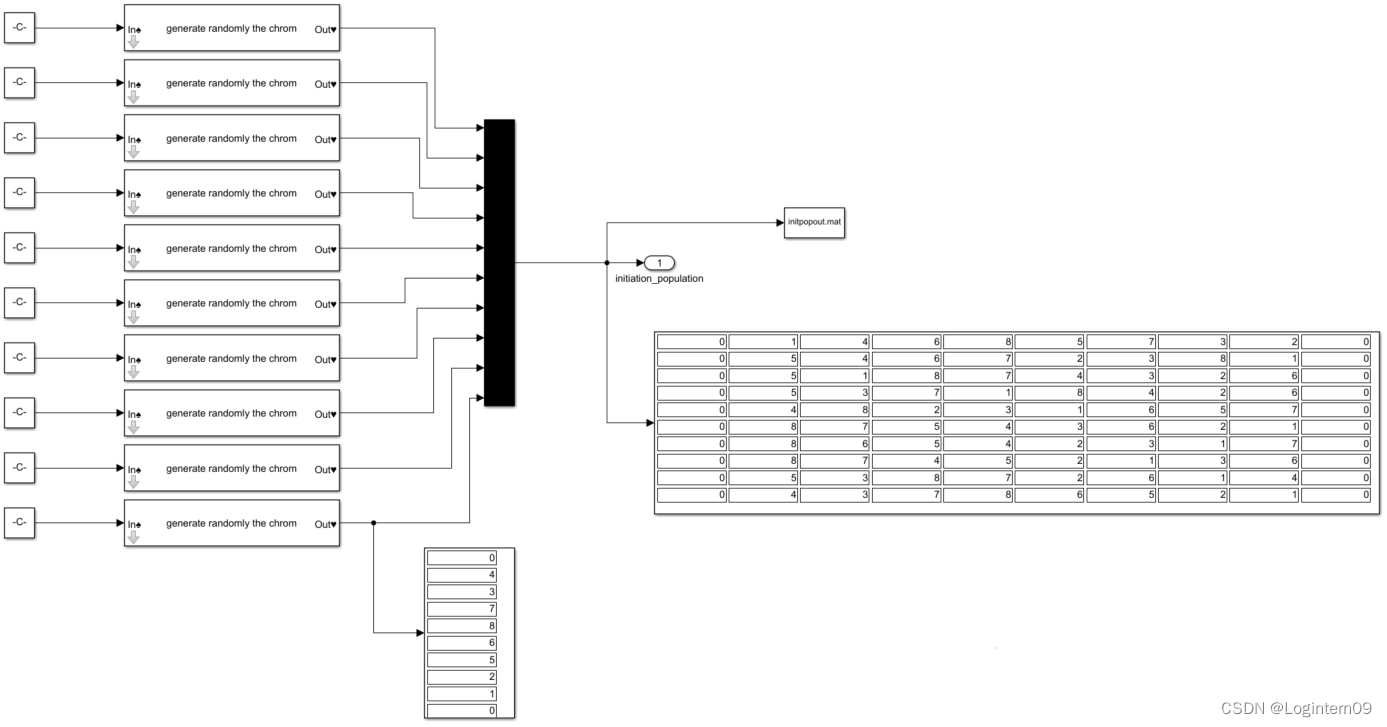
计算种群的适应度函数
将上一章节“确定种群结构”得到的输出序列存入Simulink的.mat文件,使用From File模块从initpopout.mat提取生成的种群结构作为输入,计算种群适应度函数的基本思想:使用Demux模块将1010的矩阵拆解成一维的110的列表,使用已经封装好的计算单条染色体的功能模块计算这个一维的1*10的列表,得到所有10条染色体的适应度函数(总运输距离的倒数)之后,再使用Mux模块合并列表作为一个输出信号,并且使用Min模块计算此时种群的最小运输距离。
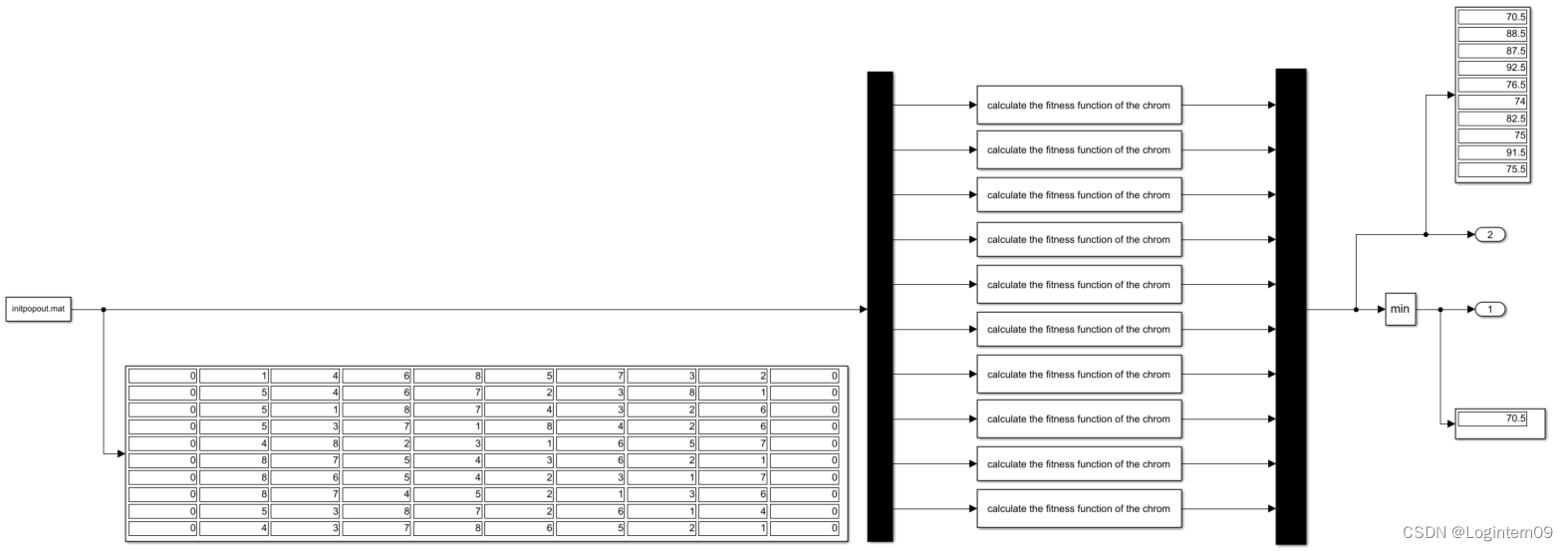
主函数
本博客针对TSP问题只进行到种群生成及种群染色体的适应度函数计算,不涉及遗传算法进化迭代的选择、交叉及变异算子。
总结以上求解TSP问题的分解步骤,可以得到下图所示的总的模型:
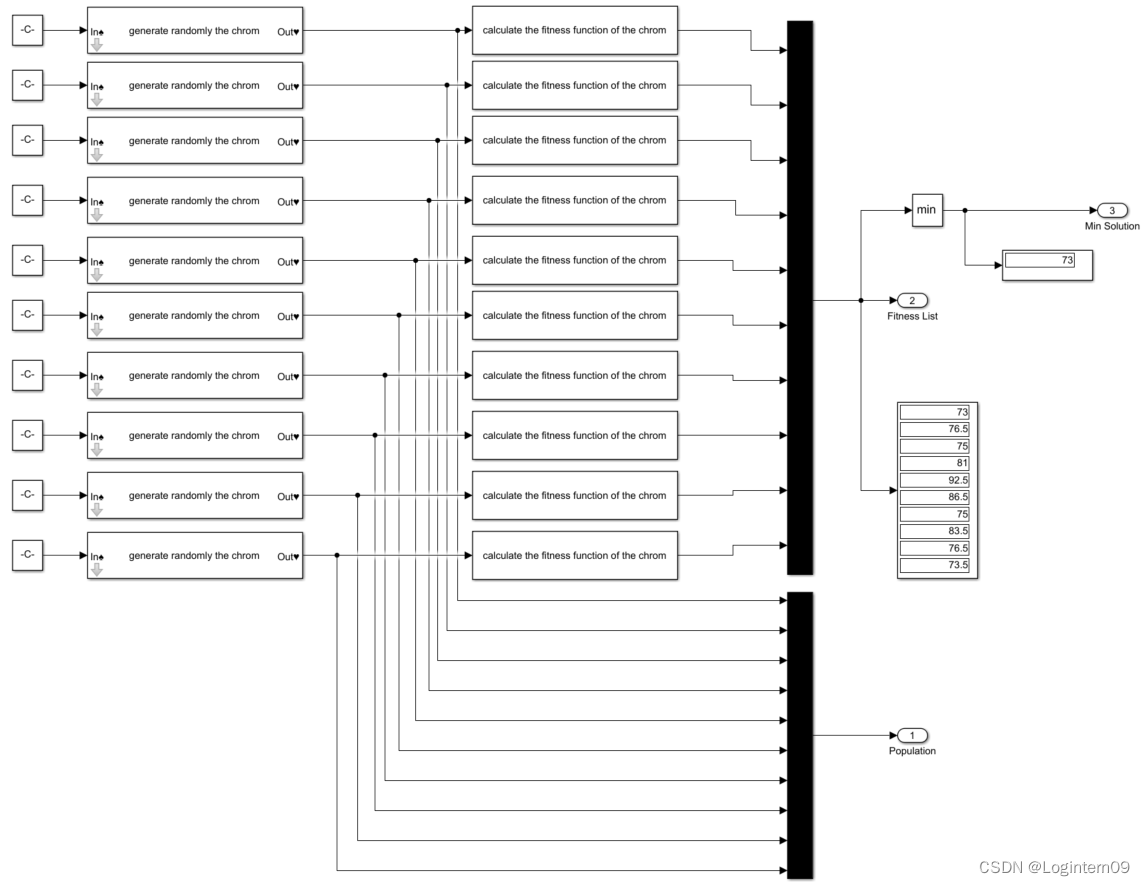
参考文献:
1.Matlab读取excel文件中的数据
https://blog.csdn.net/qq_38826019/article/details/81184811
2.MATLAB-获取正在执行的m文件路径的方法
https://blog.csdn.net/qq_43278043/article/details/115922597
3.matlab函数-fullfile-将字符合并成路径
https://blog.csdn.net/weixin_37724055/article/details/109952562
4.matlab的输出(命令窗口、fprint函数、disp函数)
https://blog.csdn.net/caomin1hao/article/details/83996365
5.matlab 分割字符串、提取文件路径及文件名
https://blog.csdn.net/u012189747/article/details/86504693
相关文章:

simulink与遗传算法结合求解TSP问题
前言:刚开始入门学习simulink,了解了基本的模块功能后想尝试从自己熟悉的领域入手,自己出题使用simulink搭建模型。选择的是TSP问题的遗传算法,考虑如何用simulink建模思想来实现一个简单TSP问题的遗传算法。 TSP问题描述 一个配…...

环境搭建-Ubuntu18.04.6系统TensorFlow BenchMark的GPU测试
1. 下载Ubuntu18.04.6镜像 登录阿里云官方镜像站:阿里巴巴开源镜像站-OPSX镜像站-阿里云开发者社区 2. 测试环境 Server OS:Ubuntu 20.04.6 LTS Kernel: Linux 5.4.0-155-generic x86-64 Docker Version:24.0.5, build ced0996 docker-com…...

C# 汇总区间
228 汇总区间 给定一个 无重复元素 的 有序 整数数组 nums 。 返回 恰好覆盖数组中所有数字 的 最小有序 区间范围列表 。也就是说,nums 的每个元素都恰好被某个区间范围所覆盖,并且不存在属于某个范围但不属于 nums 的数字 x 。 列表中的每个区间范围…...
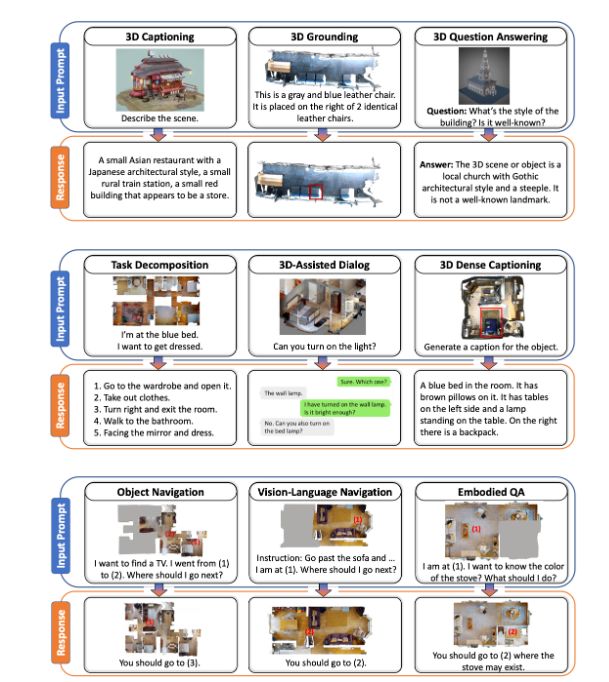
加利福尼亚大学|3D-LLM:将3D世界于大规模语言模型结合
来自加利福尼亚大学的3D-LLM项目团队提到:大型语言模型 (LLM) 和视觉语言模型 (VLM) 已被证明在多项任务上表现出色,例如常识推理。尽管这些模型非常强大,但它们并不以 3D 物理世界为基础,而 3D 物理世界涉及更丰富的概念…...
HCIA实验四
一.实验要求: 1、R4为ISP,其上只能配置IP地址;R4与其他所有直连设备间均使用共有IP; 2、R3 - R5/6/7为MGRE环境,R3为中心站点; 3、整个网络配置OSPF环境,IP基于172.16.0.0/16网段划分&#x…...

常见的算法
查找算法 基本查找 Demo1 public static boolean basicSearch(int index,int[] arr){for (int i 0; i < arr.length; i) {if (indexarr[i]){return true;}}return false; } Demo2 //顺序查找,考虑重复,返回查找内容的索引 public static ArrayLis…...
Jetbrains 2023.2教程
IDEA 2023.2 激活演示 Pycharm 2023.2 激活演示 WebStorm 2023.2 激活演示 Clion 2023.2 激活演示 DataGrip 2023.2 PhpStorm 2023.1.4 激活演示(2023.2尚未发布) RubyMine 2023.2 激活演示 获取方式 仔细看每一个工具演示的图片 本文由 mdnice …...

OpenLayers入门,OpenLayers地图初始化时如何设置默认缩放级别、设置默认地图中心点、最大缩放级别和最小缩放级别以及默认坐标系
专栏目录: OpenLayers入门教程汇总目录 前言 OpenLayers地图初始化时如何设置默认缩放级别、初始化时设置默认地图中心点、设置最大缩放级别和最小缩放级别,超过缩放级别用户无法再放大和缩小,和设置默认坐标系。 二、依赖和使用 "ol": "^6.15.1"使用…...

css实现步骤条中的横线
实现步骤中的横线,我们使用css中的after选择器,content写空,然后给这个范围设定一个绝对定位,相当于和它设置伪类选择的元素的位置,直接看代码: const commonStyle useMemo(() > ({fontSize: 30px}),[]…...
【业务功能篇57】Springboot + Spring Security 权限管理 【上篇】
4.权限管理模块开发 4.1 权限管理概述 4.1.1 权限管理的意义 后台管理系统中,通常需要控制不同的登录用户可以操作的内容。权限管理用于管理系统资源,分配用户菜单、资源权限,以及验证用户是否有访问资源权限。 4.1.2 RBAC权限设计模型 …...

云计算需求激增带来的基础设施挑战及解决方案
云计算的指数级增长迅速改变了我们消费和存储数字信息的方式。随着企业和个人越来越依赖基于云的服务和数据存储,对支持这些服务的强大且可扩展的基础设施的需求已达到前所未有的水平。 云计算需求的快速增长 我们的日常生活越来越多地被新技术所渗透。流媒体服务、…...

R语言中的函数23:zoo::rollmean, rollmax, rollmedian, rollsum等等
文章目录 函数介绍rollmean()rollmax()rollmedianrollsum 函数介绍 rollmean(x, k, fill if (na.pad) NA, na.pad FALSE, align c("center", "left", "right"), ...)rollmax(x, k, fill if (na.pad) NA, na.pad FALSE, align c("cen…...
数据结构—数组和广义表
4.2数组 数组:按一定格式排列起来的,具有相同类型的数据元素的集合。 **一维数组:**若线性表中的数据元素为非结果的简单元素,则称为一维数组。 **一维数组的逻辑结构:**线性结构,定长的线性表。 **声明…...

服务器负载均衡算法有哪些
算法举例 服务器负载均衡算法是用于分配网络流量到多个服务器的策略,以实现负载均衡和提高系统性能。以下是一些常见的服务器负载均衡算法的详细说明: 轮询(Round Robin)算法: 轮询算法是最简单且常见的负载均衡算法之…...

2023年深圳杯数学建模B题电子资源版权保护问题
2023年深圳杯数学建模 B题 电子资源版权保护问题 原题再现: 版权又称著作权,包括发表权、署名权、修改权、保护作品完整权、复制权、发行权、出租权、展览权、表演权、放映权、广播权、信息网络传播权、摄制权、改编权、翻译权、汇编权及应当由著作权人…...

Easyui中datagrid切换页码后,再次根据其他条件查询,重置为第一页,序号从1开始显示
Easyui中datagrid切换页码后,再次根据其他条件查询,无法将序号重置为1开始显示 1、查询按钮2、datagrid的查询方法3、datagrid点击分页4、重置方法 1、查询按钮 <a href"javascript:Query(1,true)" id"btnQuery" class"eas…...

随笔03 考研笔记整理
图源:文心一言 上半年的博文整理,下半年依然会更新考研类的文章,有需要的小伙伴看向这里~~🧩🧩 另外,这篇文章可能是我上半年的努力成果之一,因此仅关注博主的小伙伴能够查看它~~ᾞ…...
一次线上OOM问题的个人复盘
我们一个java服务上线后,偶尔会发生内存OOM(Out Of Memory)问题,但由于OOM导致服务不响应请求,健康检查多次不通过,最后部署平台kill了java进程,这导致定位这次OOM问题也变得困难起来。 最终,在多次review代…...

【机器学习】基础知识点的汇总与总结!更新中
文章目录 一、监督学习1.1、单模型1.1.1、线性回归1.1.2、逻辑回归(Logistic Regression)1.1.3、K近邻算法(KNN)1.1.4、决策树1.1.5、支持向量机(SVM)1.1.6、朴素贝叶斯 1.2、集成学习1.2.1、Boosting1&…...

NLP杂记
来京一周余,初病将愈,终跑通llama及ViT,记于此—— 之前都是做的图像,大模型迁移基本上都是NLP相关的知识,很多东西和CV差距还是有点,再加上大模型对算力要求较高,基于云的操作对我一个习惯在本…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...
