数据结构—数组和广义表
4.2数组
数组:按一定格式排列起来的,具有相同类型的数据元素的集合。
**一维数组:**若线性表中的数据元素为非结果的简单元素,则称为一维数组。
**一维数组的逻辑结构:**线性结构,定长的线性表。
**声明格式:**数据类型 变量名称 [长度] ;
例如:int num[5] = {0,1,2,3,4};
**二维数组:**若一维数组中的数据元素又是一维数组结构,则称为二维数组。
二维数组的逻辑结构:
- 非线性结构:每一个数据元素既在一个行表中,又在一个列表中。
- 线性结构定长的线性表:该线性表的每个数据元素也是一个定长的线性表。
**声明格式:**数据类型 变量名称 [行数] [列数];
例如:int num [5] [8];
在C语言中,一个二维数组类型也可以定义为一维数组类型(其分量类型为一维数组类型),即:
typedef int array2[m][n];
等价于:typedef int array1[n];typedef array1 array2[m];
**三维数组:**若二维数组中的元素又是一个一维数组,则称作三维数组。
**n维数组:**若 n - 1 维数组中的元素又是一个一维数组结构,则称作 n 维数组。
**结论:**线性表结构是数组结构的一个特例,而数组结构又是线性表结构的扩展。
**数组特点:**结构固定——定义后,维数和维界不再改变。
**数组基本操作:**除了结构的初始化和销毁之外,只有取元素和修改元素值的操作。
4.2.1数组的顺序存储结构
数组特点:结构固定——维数和维界不变。
一般都是采用顺序存储结构来表示数组。
**注意:**数组可以是多维的,但存储数据元素的内存单元地址是一维的,因此,在存储数组结构之前,需要解决将多维关系映射到一维关系的问题。
一维数组:
例:有数组定义:int a[5]
每个元素占用4字节,假设a[0]存储在2000单元,a[3]地址是多少?
LOC(0) = a = 2000 L=4
LOC(3) = 3*4+2000
LOC(i) = i*L + 首地址
存储单元是一维结构,而数组是个多维结构,则用一组连续存储单元存放数组的数据元素就有个次序约定问题。
二维数组可有两种存储方式:
-
以行序为主序;
设数组开始存储位置LOC(0,0),存储每个元素需要L个存储单元
数组元素a[i] [j]的存储位置是:LOC(i,j)=LOC(0,0) + (n * i + j) * L
-
以列序为主序。
**三维数组:**按页/行/列存放,页优先的顺序存储。
4.2.2特殊矩阵的压缩存储
**矩阵:**一个由 m*n 个元素排成的 m 行 n 列的表。
**矩阵的常规存储:**将矩阵描述为一个二维数组。
矩阵的常规存储的特点:
- 可以对其元素进行随机存取。
- 矩阵运算非常简单;存储的密度为1.
**不适宜常规存储的矩阵:**值相同的元素很多且呈某种规律分布;零元素多。
**矩阵的压缩存储:**为多个相同的非零元素只分配一个存储空间;对零元素不分配空间。
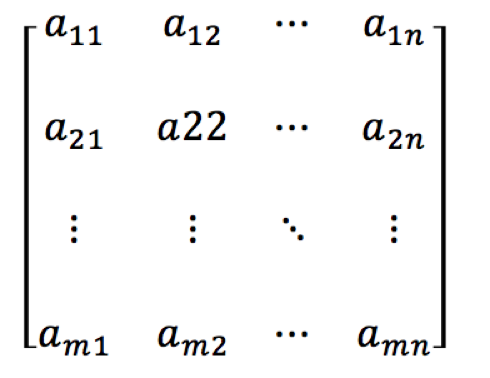
1、什么是压缩存储
若多个数据元素的值都相同,则只分配一个元素值的存储空间,且零元素不占存储空间。
2、什么样的矩阵能够压缩?
一些特殊矩阵,如:对称矩阵,对角矩阵,三角矩阵,稀疏矩阵等。
3、什么叫稀疏矩阵?
矩阵中非零元素的个数较少(一般小于5%)
1.对称矩阵
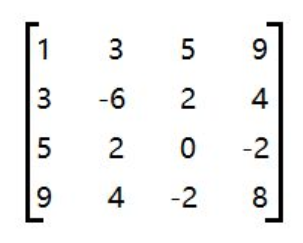
**【特点】:**在 n*n 的矩阵 a 中,满足如下性质:aij=aji(1≤i , j≤n)
**【存储方法】:**只存储下(或者上)三角(包括主对角线)的数据元素。共占用 n(n+1)/2个元素空间。
**【存储结构】:**对称矩阵上下三角中的元素数均为:n(n+1)/2
可以以行序为主序将元素存放在一个一维数组 sa[ n(n+1)/2 ]中。
2.三角矩阵
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6FofxLkg-1690537372616)(https://tse1-mm.cn.bing.net/th?id=OIF-C.uHr%2bn0jNJ2j8NRD2iircPA&pid=ImgDet&rs=1)]
**【特点】:**对角线以下(或者以上)的数据元素(不包括对角线)全部为常数c。
**【存储方法】:**重复元素c共享一个元素存储空间,共占用n(n+1)/2+1个元素空间:[1…n(n+1)/2+1]
上三角矩阵:

下三角矩阵:
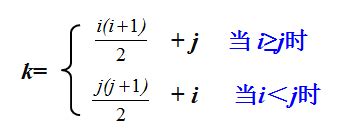
3.对角矩阵(带状矩阵)

**【特点】:**在n*n的方阵中,所有非零元素都集中在以主对角线为中心的带状区域中,区域外的值全为0,则称为对角矩阵。常见的有三对角矩阵、五对角矩阵、七对角矩阵等。

4.稀疏矩阵
**稀疏矩阵:**设在 m*n 的矩阵中有 t 个非零元素。
令 δ = t / (m*n)
当 δ ≤ 0.05 时称为稀疏矩阵。
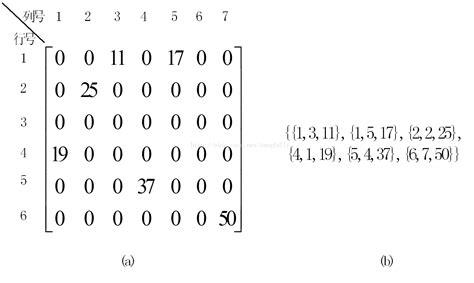
**压缩存储原则:**存各非零元素的值,行列位置和矩阵的行列数。
4.1三元组顺序表

注意:为更可靠描述,通常再加一个“总体”信息:即总行数、总列数、非零元素总个数。
三元组顺序表又称有序的双下标法。
三元组顺序表的优点:非零元素在表中按行序有序存储,因此便于进行依行顺序处理的矩阵运算。
三元组顺序表的缺点:不能随机存取。若按行号存取某一行中的非零元素,则需从头开始进行查找。
4.2十字链表
-
**优点:**它能够灵活地插入因运算而产生的新的非零元素,删除因运算而产生的新的零元素,实现矩阵的各种运算。
-
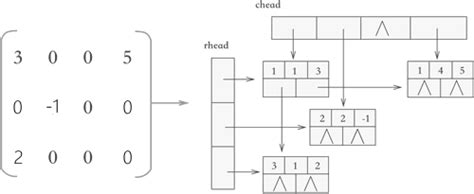
在十字链表中,矩阵的每一个非零元素用一个结点表示,该结点除了(row,col,value)以外,还要有两个域:
- right:用于链接同一行中的下一个非零元素。
- down:用以链接同一列中的下一个非零元素。
-
十字链表中结点的结构示意图:

4.3广义表
4.3.1广义表定义
广义表(又称列表Lists)是n≥0个元素 a0,a1,…,an-1的有限序列,其中每一个ai或者是原子,或者是一个广义表。
例如:中国举办的国际足球邀请赛,参赛队伍名单可表示如下:
(阿根廷,巴西,德国,法国,(),西班牙,意大利,英国,(国家队,山东鲁能,广州恒大))
在这个表中,叙利亚队应排在法国队的后面,但未能参加,成为空表。国家队,山东鲁队,广州恒大均作为东道主的参赛队参加,构成一个小的线性表,成为原线性表的一个数据元素。这种拓宽了的线性表就是广义表。
-
广义表通常记作:LS=( a1,a2,…,an
-
习惯上,一般用大写字母表示广义表,小写字母表示原子。
-
**表头:**若LS非空(n≥1),则其第一个元素a1就是表头。记作head(LS)=a1.
注意:表头可以是原子,也可以是子表。
-
表尾:除表头之外的其他元素组成的表。记作tail(LS)=(a2,…,an)
注意:表尾不是最后一个元素,而是一个子表。
例如:(1) A=() 空表,长度为0
(2)B=(( )) 长度为1,表头、表尾均为()。
(3)C=(a,(b,c)) 长度为2,由原子a和子表(b,c)构成。表头为a,表尾为((b,c))
(4)D=(x,y,z) 长度为3,每一项都是原子。表头为x,表尾为(y,z)
(5)E=(C,D) 长度为2,每一项都是子表。表头为C,表尾为(D)
(6)F=(a,F) 长度为2,第一项为原子,第二项为它本身。表头为a,表尾为(F)。F=(a,(a,(a,…)))
4.3.2广义表的性质
-
广义表的数据元素有相对应次序;一个直接前驱和一个直接后继。
-
广义表的长度定义为最外层所包括元素的个数,如C=(a,(b,c))是长度为2的广义表。
-
广义表的深度定义为该广义表展开后所含括号的重数。
注意:“原子”的深度为0;“空表”的深度为1。
-
广义表可以为其他广义表共享:如:广义表B就共享表A。在B中不必列出A的值,而是通过名称来引用。B=(A)
-
广义表可以是一个递归的表。
注意:递归表的深度是无穷值,长度是有限值。
-
广义表是一个多层次结构,广义表的元素可以是单元数,也可以是子表,而子表的元素还可以是子表。
4.3.3广义表和线性表的区别
广义表可以看成是线性表的推广,线性表是广义表的特例。
广义表的结构相当灵活,在某种前提下,它可以兼容线性表、数组、数和有向图等各种常见的数据结构。
当二维数组的每行(或每列)作为子表处理时,二维数组即为一个广义表。
另外,数和有向图也可以用广义表来表示。
由于广义表不仅集中了线性表,数组,数和有向图等常见数据结构的特点,而且可有效地利用存储空间,因此在计算机的许多应用领域都有成功使用广义表的实例。
4.3.4广义表的基本运算
- 求表头GetHead(L):非空广义表的第一个元素,可以是一个单一元素,也可以是一个子表。
- 求表尾GetTail(L):非空广义表除去表头元素以外其他元素所构成的表,表尾一定是一个表。
相关文章:
数据结构—数组和广义表
4.2数组 数组:按一定格式排列起来的,具有相同类型的数据元素的集合。 **一维数组:**若线性表中的数据元素为非结果的简单元素,则称为一维数组。 **一维数组的逻辑结构:**线性结构,定长的线性表。 **声明…...

服务器负载均衡算法有哪些
算法举例 服务器负载均衡算法是用于分配网络流量到多个服务器的策略,以实现负载均衡和提高系统性能。以下是一些常见的服务器负载均衡算法的详细说明: 轮询(Round Robin)算法: 轮询算法是最简单且常见的负载均衡算法之…...

2023年深圳杯数学建模B题电子资源版权保护问题
2023年深圳杯数学建模 B题 电子资源版权保护问题 原题再现: 版权又称著作权,包括发表权、署名权、修改权、保护作品完整权、复制权、发行权、出租权、展览权、表演权、放映权、广播权、信息网络传播权、摄制权、改编权、翻译权、汇编权及应当由著作权人…...

Easyui中datagrid切换页码后,再次根据其他条件查询,重置为第一页,序号从1开始显示
Easyui中datagrid切换页码后,再次根据其他条件查询,无法将序号重置为1开始显示 1、查询按钮2、datagrid的查询方法3、datagrid点击分页4、重置方法 1、查询按钮 <a href"javascript:Query(1,true)" id"btnQuery" class"eas…...

随笔03 考研笔记整理
图源:文心一言 上半年的博文整理,下半年依然会更新考研类的文章,有需要的小伙伴看向这里~~🧩🧩 另外,这篇文章可能是我上半年的努力成果之一,因此仅关注博主的小伙伴能够查看它~~ᾞ…...
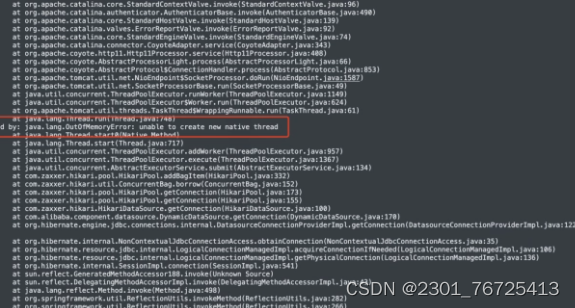
一次线上OOM问题的个人复盘
我们一个java服务上线后,偶尔会发生内存OOM(Out Of Memory)问题,但由于OOM导致服务不响应请求,健康检查多次不通过,最后部署平台kill了java进程,这导致定位这次OOM问题也变得困难起来。 最终,在多次review代…...

【机器学习】基础知识点的汇总与总结!更新中
文章目录 一、监督学习1.1、单模型1.1.1、线性回归1.1.2、逻辑回归(Logistic Regression)1.1.3、K近邻算法(KNN)1.1.4、决策树1.1.5、支持向量机(SVM)1.1.6、朴素贝叶斯 1.2、集成学习1.2.1、Boosting1&…...

NLP杂记
来京一周余,初病将愈,终跑通llama及ViT,记于此—— 之前都是做的图像,大模型迁移基本上都是NLP相关的知识,很多东西和CV差距还是有点,再加上大模型对算力要求较高,基于云的操作对我一个习惯在本…...
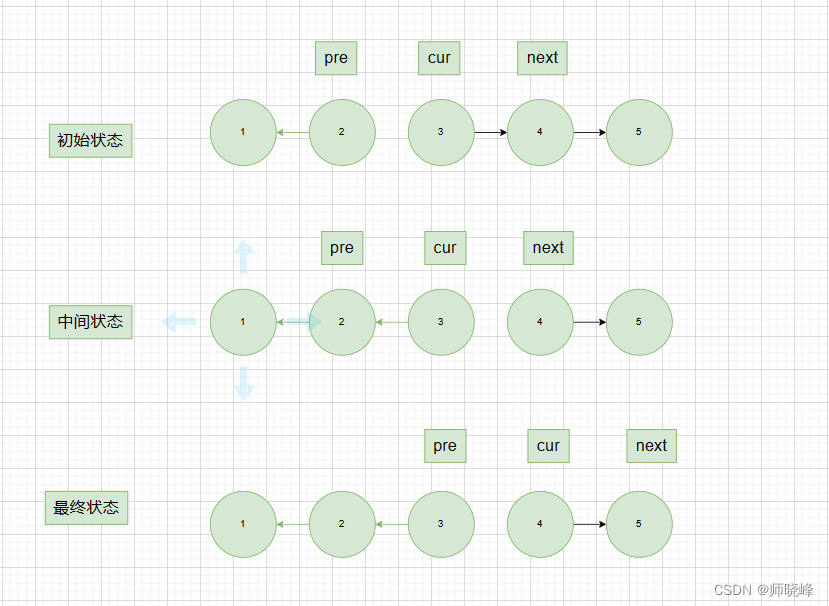
算法通过村第二关-链表白银笔记
文章目录 再战链表|反转链表剑指 Offer II 024. 反转链表熟练掌握这两种解法建立头节点的解决思路不采用建立头节点的方法采用循环/递归的方式解决 总结 再战链表|反转链表 提示:多拿些酒来,因为生命只有乌有。 剑指 Offer II 024. 反转链表 如果不使用…...
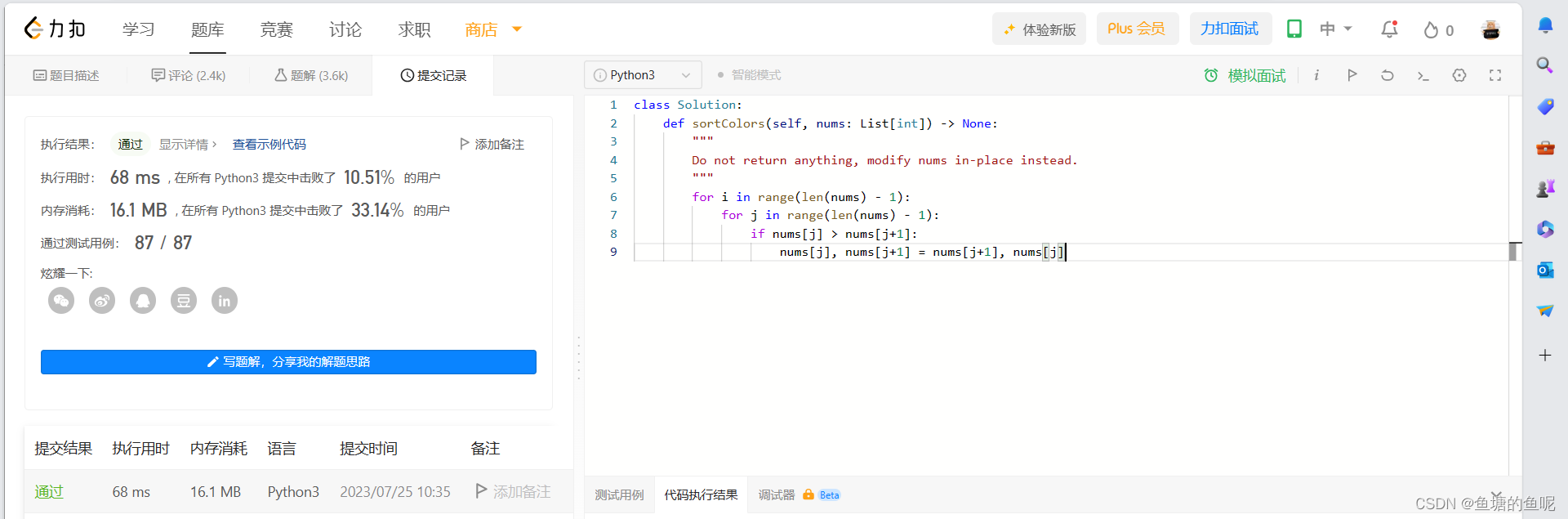
力扣题库刷题笔记75--颜色分类
1、题目如下: 2、个人Pyhon代码实现如下: 第一种思路是取巧,通过计数0、1、2的个数,去替换nums 备注第10行代码在本地可以跑过,但是力扣跑不过,所以就用了第10-16行代码进行替换 第二种思路是通过冒泡排序去…...

《面试1v1》如何提高远程用户的吞吐量
🍅 作者简介:王哥,CSDN2022博客总榜Top100🏆、博客专家💪 🍅 技术交流:定期更新Java硬核干货,不定期送书活动 🍅 王哥多年工作总结:Java学习路线总结…...
论文笔记--Distilling the Knowledge in a Neural Network
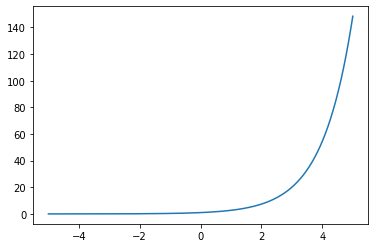
论文笔记--Distilling the Knowledge in a Neural Network 1. 文章简介2. 文章概括3 文章重点技术3.1 Soft Target3.2 蒸馏Distillation 4. 文章亮点5. 原文传送门 1. 文章简介 标题:Distilling the Knowledge in a Neural Network作者:Hinton, Geoffre…...
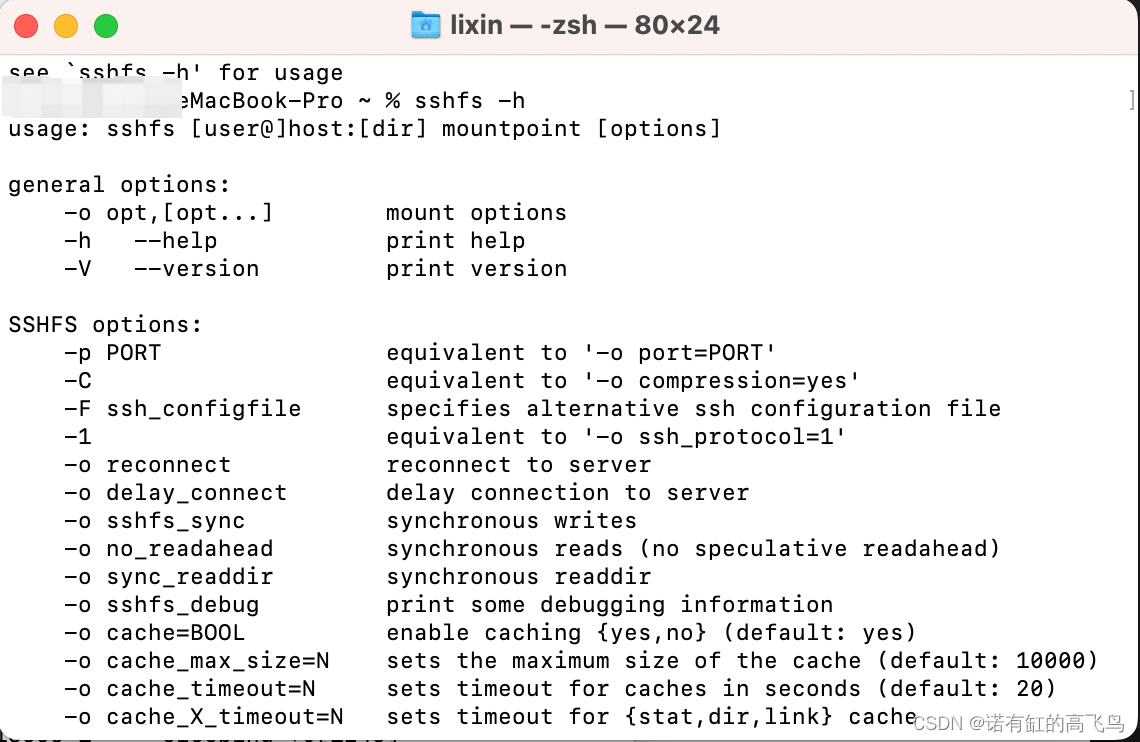
Mac上安装sshfs
目录 写在前面安装使用参考完 写在前面 1、本文内容 Mac上安装sshfs 2、平台 mac 3、转载请注明出处: https://blog.csdn.net/qq_41102371/article/details/130156287 安装 参考:https://ports.macports.org/port/sshfs/ 通过port安装 点击啊insta…...
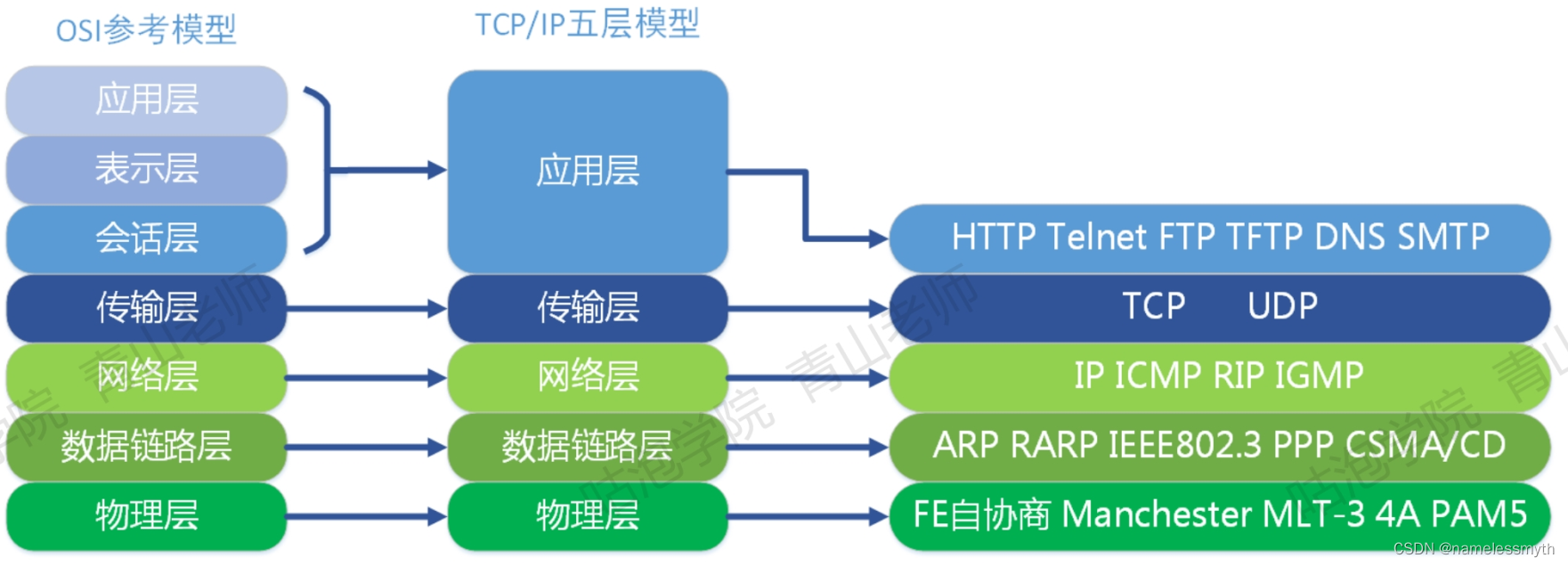
MQ公共特性介绍 (ActiveMQ, RabbitMQ, RocketMQ, Kafka对比)
本章介绍 本文主要介绍所有MQ框架都具备的公共特点,同时对比了一些目前比较主流MQ框架的优缺点,给大家做技术选型作参考。 文章目录 本章介绍MQ介绍适用场景异步通信案例一案例二 系统解耦削峰填谷广播通信总结 缺点MQ对比APQP历史AMQP是什么 MQ介绍 M…...
灵雀云Alauda MLOps 现已支持 Meta LLaMA 2 全系列模型
在人工智能和机器学习领域,语言模型的发展一直是企业关注的焦点。然而,由于硬件成本和资源需求的挑战,许多企业在应用大模型时仍然面临着一定的困难。为了帮助企业更好地应对上述挑战,灵雀云于近日宣布,企业可通过Alau…...

技术方案模版
技术方案模板 概述 1.1 术语 名称 说明 1.2 需求背景 来自产品的需求可以引用PRD和设计稿 技术类的改造需要写明背景业务用例分析 从需求中抽象出的核心用例详细设计 3.1 应用架构 3.2 模型设计 领域模型的关系,可以用UML 类图来实现 3.3. 详细实现 可以通过时序图…...

【Linux命令200例】cut强大的文本处理工具
🏆作者简介,黑夜开发者,全栈领域新星创作者✌,2023年6月csdn上海赛道top4。 🏆本文已收录于专栏:Linux命令大全。 🏆本专栏我们会通过具体的系统的命令讲解加上鲜活的实操案例对各个命令进行深入…...

《论文阅读》具有特殊Token和轮级注意力的层级对话理解 ICLR 2023
《论文阅读》具有特殊Token和轮级注意力的层级对话理解 前言简介问题定义模型构建知识点Intra-turn ModelingInter-turn Modeling分类前言 你是否也对于理解论文存在困惑? 你是否也像我之前搜索论文解读,得到只是中文翻译的解读后感到失望? 小白如何从零读懂论文?和我一…...

C# 定时器封装版
一、概述 在 Winform 等平台开发中,经常会用到定时器的功能,但项目定时器一旦写多了,容易使软件变卡,而且运行时间长了会造成软件的闪退,这个可能是内存溢出造成的,具体原因我也没去深究,另一个…...

前端学习——Vue (Day4)
组件的三大组成部分 组件的样式冲突 scoped <template><div class"base-one">BaseOne</div> </template><script> export default {} </script><style scoped> /* 1.style中的样式 默认是作用到全局的2.加上scoped可以让样…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...
