论文笔记--Distilling the Knowledge in a Neural Network
论文笔记--Distilling the Knowledge in a Neural Network
- 1. 文章简介
- 2. 文章概括
- 3 文章重点技术
- 3.1 Soft Target
- 3.2 蒸馏Distillation
- 4. 文章亮点
- 5. 原文传送门
1. 文章简介
- 标题:Distilling the Knowledge in a Neural Network
- 作者:Hinton, Geoffrey, Oriol Vinyals, Jeff Dean
- 日期:2015
- 期刊:arxiv
2. 文章概括
文章提出了一种将大模型压缩的新的思路:蒸馏distillation。通过蒸馏,可以将很大的模型压缩为轻量级的模型,从而提升推理阶段的速率。
3 文章重点技术
3.1 Soft Target
随着模型的参数量越来越大,如何从训练好的大模型(教师模型)学习一个轻量级的小模型(学生模型)是一个重要课题。传统的hard-target训练直接学习大模型的预测结果,无法学习到不正确的类别之间的相对关系。比如给定一张宝马的照片,假设教师模型给出的预测结果为宝马,学生模型只从教师模型中学习到“宝马”这一个标签信息。事实上,教师模型还会给出其它类别的信息,比如将宝马预测为垃圾车为0.02,将宝马预测为胡萝卜的概率仅为0.0001,但学生模型没有学习到垃圾车和胡萝卜之间的区别。
我们需要一种方法来使得学生学习到正确的标签,以及错误标签的相对关系。文章提出“soft-target",即通过学习教师模型的预测概率分布来训练小模型。
3.2 蒸馏Distillation
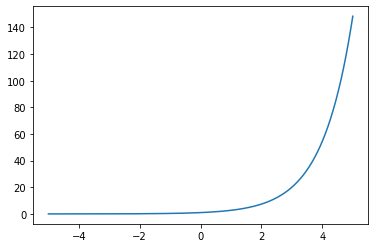
对一个分类模型,假设教师模型的输出层给出的logits为 z i z_i zi,然后通过计算Softmax得到预测概率: q i = exp ( z i / T ) ∑ j exp ( z j / T ) q_i = \frac {\exp (z_i/T)}{\sum_j \exp (z_j/T)} qi=∑jexp(zj/T)exp(zi/T),其中相比于传统的SoftMax增加了 T T T表示温度,用于控制输出概率分布的平滑度。 T T T越大,不同类别之间的差异越不明显,即分布越平滑。可以参考 e x p exp exp的函数曲线来理解:给定 x 1 , x 2 x_1, x_2 x1,x2,由当 T T T越大时, x 1 / T , x 2 / T x_1/T, x_2/T x1/T,x2/T对应的导数越小(导数即为 exp ( x ) \exp(x) exp(x),也可参考下图),从而差距越小,分布越平滑。当 T = 1 T=1 T=1时,即传统的Softmax。
我们希望学生模型满足:1) 模型可以学习到教师模型的预测概率,即soft targets; 2)学生模型可以预测真实的标签。从而我们可以考虑2个目标函数: L hard \mathcal{L}_{\text{hard}} Lhard和 L soft \mathcal{L}_{\text{soft}} Lsoft。首先我们记学生模型和教师模型的logits分别为 z i , v i z_i, v_i zi,vi,预测概率分别为 q i , p i q_i, p_i qi,pi,真实标签为labels,则
- L hard = Cross Entropy ( labels , arg max i ( exp ( z i / T ) ∑ j exp ( z j / T ) ) ) \mathcal{L}_{\text{hard}}=\text{Cross Entropy}\left(\text{labels}, \argmax_i \left(\frac {\exp (z_i/T)}{\sum_j \exp (z_j/T)}\right)\right) Lhard=Cross Entropy(labels,argmaxi(∑jexp(zj/T)exp(zi/T)))
- L soft = Cross Entropy ( p , q ) = Cross Entropy ( ( exp ( v i / T ) ∑ j exp ( v j / T ) ) , ( exp ( z i / T ) ∑ j exp ( z j / T ) ) ) \mathcal{L}_{\text{soft}}=\text{Cross Entropy}\left(p, q \right) =\text{Cross Entropy}\left((\frac {\exp (v_i/T)}{\sum_j \exp (v_j/T)}), (\frac {\exp (z_i/T)}{\sum_j \exp (z_j/T)})\right) Lsoft=Cross Entropy(p,q)=Cross Entropy((∑jexp(vj/T)exp(vi/T)),(∑jexp(zj/T)exp(zi/T)))
考虑 L soft \mathcal{L}_{\text{soft}} Lsoft的梯度 ∂ L soft ∂ z k = ∂ ( − ∑ i p i log q i ) ∂ z k = − ∑ i p i q i ∂ q i ∂ z k = − p k q k ∂ q k ∂ z k − ∑ i ≠ k p i q i ∂ q i ∂ z k = − 1 T p k q k q k ( 1 − q k ) + ∑ i ≠ k p i q i exp ( z i / T ) ( ∑ j exp ( z j / T ) ) 2 1 T exp ( z k / T ) = 1 T ( − p k ( 1 − q k ) + ∑ i ≠ k p i q i q i q k ) = 1 T ( − p k + ∑ i p i q k ) = 1 T ( q k − p k ) = 1 T ( exp ( z k / T ) ∑ j exp ( z j / T ) − exp ( v k / T ) ∑ j exp ( v j / T ) ) \frac {\partial \mathcal{L}_{\text{soft}}}{\partial z_k} = \frac {\partial (-\sum_i p_i \log q_i)}{\partial z_k} = -\sum_i \frac {p_i}{q_i} \frac{\partial q_i}{\partial z_k} = -\frac {p_k}{q_k} \frac{\partial q_k}{\partial z_k}-\sum_{i\neq k} \frac {p_i}{q_i} \frac{\partial q_i}{\partial z_k} \\=-\frac 1T \frac {p_k}{q_k} q_k (1-q_k) +\sum_{i\neq k} \frac {p_i}{q_i} \frac {\exp (z_i/T)}{(\sum_j \exp (z_j/T))^2} \frac 1T \exp (z_k/T) \\= \frac 1T (-p_k (1-q_k) + \sum_{i\neq k} \frac {p_i}{q_i} q_i q_k )= \frac 1T (-p_k + \sum_i p_i q_k ) \\= \frac 1T (q_k - p_k) = \frac 1T \left(\frac {\exp (z_k/T)}{\sum_j \exp (z_j/T)} - \frac {\exp (v_k/T)}{\sum_j \exp (v_j/T)}\right) ∂zk∂Lsoft=∂zk∂(−∑ipilogqi)=−i∑qipi∂zk∂qi=−qkpk∂zk∂qk−i=k∑qipi∂zk∂qi=−T1qkpkqk(1−qk)+i=k∑qipi(∑jexp(zj/T))2exp(zi/T)T1exp(zk/T)=T1(−pk(1−qk)+i=k∑qipiqiqk)=T1(−pk+i∑piqk)=T1(qk−pk)=T1(∑jexp(zj/T)exp(zk/T)−∑jexp(vj/T)exp(vk/T)),当 T T T相比于 z i , v i z_i, v_i zi,vi等logits量级比较高时,有 z i / T → 0 , v i / T → 0 z_i/T\to 0, v_i/T \to 0 zi/T→0,vi/T→0,从而由泰勒公式上式近似为 ∂ L soft ∂ z k ≈ 1 T ( 1 + z k / T N + ∑ j z j / T − 1 + v k / T N + ∑ j v j / T ) \frac {\partial \mathcal{L}_{\text{soft}}}{\partial z_k} \approx \frac 1T \left(\frac {1+z_k/T}{N + \sum_j z_j/T} - \frac {1+v_k/T}{N + \sum_j v_j/T}\right) ∂zk∂Lsoft≈T1(N+∑jzj/T1+zk/T−N+∑jvj/T1+vk/T),假设logits都是零均值的,则有 ∂ L soft ∂ z k ≈ 1 N T 2 ( z k − v k ) \frac {\partial \mathcal{L}_{\text{soft}}}{\partial z_k} \approx \frac 1{NT^2} (z_k - v_k) ∂zk∂Lsoft≈NT21(zk−vk)。从而当温度比较高时,我们的目标近似为最小化 1 2 ( z k − v k ) 2 \frac 12 (z_k - v_k)^2 21(zk−vk)2(上式的原函数,不考虑常数项),即最小化logits的MSE函数。温度越低,我们越关注小于均值的logits。
最终的损失函数为上述hard和soft损失的加权求和。
4. 文章亮点
文章提出了基于soft-target的蒸馏方法,可以让学生模型学习到教师模型的预测概率分布,从而增强学生模型的泛化能力。实验表明,在MNIST和speech recognition数据上,基于soft target的学生模型可以提取到更多有用的信息,且可以有效防止过拟合的发生。
5. 原文传送门
Distilling the Knowledge in a Neural Network
相关文章:

论文笔记--Distilling the Knowledge in a Neural Network
论文笔记--Distilling the Knowledge in a Neural Network 1. 文章简介2. 文章概括3 文章重点技术3.1 Soft Target3.2 蒸馏Distillation 4. 文章亮点5. 原文传送门 1. 文章简介 标题:Distilling the Knowledge in a Neural Network作者:Hinton, Geoffre…...
Mac上安装sshfs
目录 写在前面安装使用参考完 写在前面 1、本文内容 Mac上安装sshfs 2、平台 mac 3、转载请注明出处: https://blog.csdn.net/qq_41102371/article/details/130156287 安装 参考:https://ports.macports.org/port/sshfs/ 通过port安装 点击啊insta…...
MQ公共特性介绍 (ActiveMQ, RabbitMQ, RocketMQ, Kafka对比)
本章介绍 本文主要介绍所有MQ框架都具备的公共特点,同时对比了一些目前比较主流MQ框架的优缺点,给大家做技术选型作参考。 文章目录 本章介绍MQ介绍适用场景异步通信案例一案例二 系统解耦削峰填谷广播通信总结 缺点MQ对比APQP历史AMQP是什么 MQ介绍 M…...
灵雀云Alauda MLOps 现已支持 Meta LLaMA 2 全系列模型
在人工智能和机器学习领域,语言模型的发展一直是企业关注的焦点。然而,由于硬件成本和资源需求的挑战,许多企业在应用大模型时仍然面临着一定的困难。为了帮助企业更好地应对上述挑战,灵雀云于近日宣布,企业可通过Alau…...

技术方案模版
技术方案模板 概述 1.1 术语 名称 说明 1.2 需求背景 来自产品的需求可以引用PRD和设计稿 技术类的改造需要写明背景业务用例分析 从需求中抽象出的核心用例详细设计 3.1 应用架构 3.2 模型设计 领域模型的关系,可以用UML 类图来实现 3.3. 详细实现 可以通过时序图…...

【Linux命令200例】cut强大的文本处理工具
🏆作者简介,黑夜开发者,全栈领域新星创作者✌,2023年6月csdn上海赛道top4。 🏆本文已收录于专栏:Linux命令大全。 🏆本专栏我们会通过具体的系统的命令讲解加上鲜活的实操案例对各个命令进行深入…...

《论文阅读》具有特殊Token和轮级注意力的层级对话理解 ICLR 2023
《论文阅读》具有特殊Token和轮级注意力的层级对话理解 前言简介问题定义模型构建知识点Intra-turn ModelingInter-turn Modeling分类前言 你是否也对于理解论文存在困惑? 你是否也像我之前搜索论文解读,得到只是中文翻译的解读后感到失望? 小白如何从零读懂论文?和我一…...

C# 定时器封装版
一、概述 在 Winform 等平台开发中,经常会用到定时器的功能,但项目定时器一旦写多了,容易使软件变卡,而且运行时间长了会造成软件的闪退,这个可能是内存溢出造成的,具体原因我也没去深究,另一个…...

前端学习——Vue (Day4)
组件的三大组成部分 组件的样式冲突 scoped <template><div class"base-one">BaseOne</div> </template><script> export default {} </script><style scoped> /* 1.style中的样式 默认是作用到全局的2.加上scoped可以让样…...
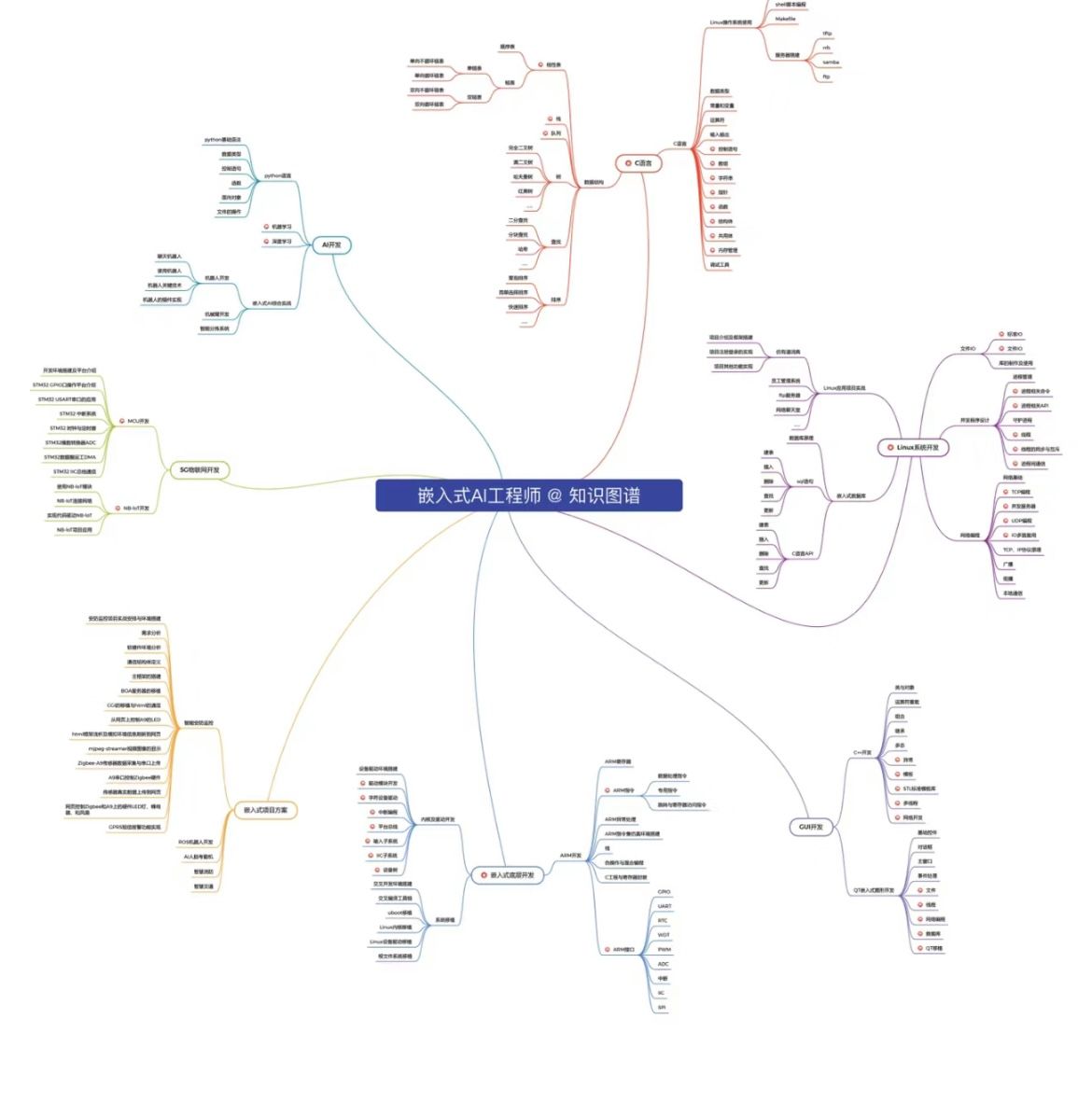
如果你是一个嵌入式面试官,你会问哪些问题?
以下是一些嵌入式面试中可能会问到的问题: 1.你对嵌入式系统有什么理解?它们与桌面或服务器系统有什么不同? 2.你用过哪些单片机和微处理器?对其中哪一款最熟悉? 3.你用什么编程语言编写嵌入式软件?你觉…...
学习笔记十三:云服务器通过Kubeadm安装k8s1.25,供后续试验用
Kubeadm安装k8s1.25 k8s环境规划:初始化安装k8s集群的实验环境先建生产环境服务器,后面可以通过生成镜像克隆node环境修改主机名配置yum源关闭防火墙关闭selinux配置时间同步配置主机 hosts 文件,相互之间通过主机名互相访问 **192.168.40.18…...
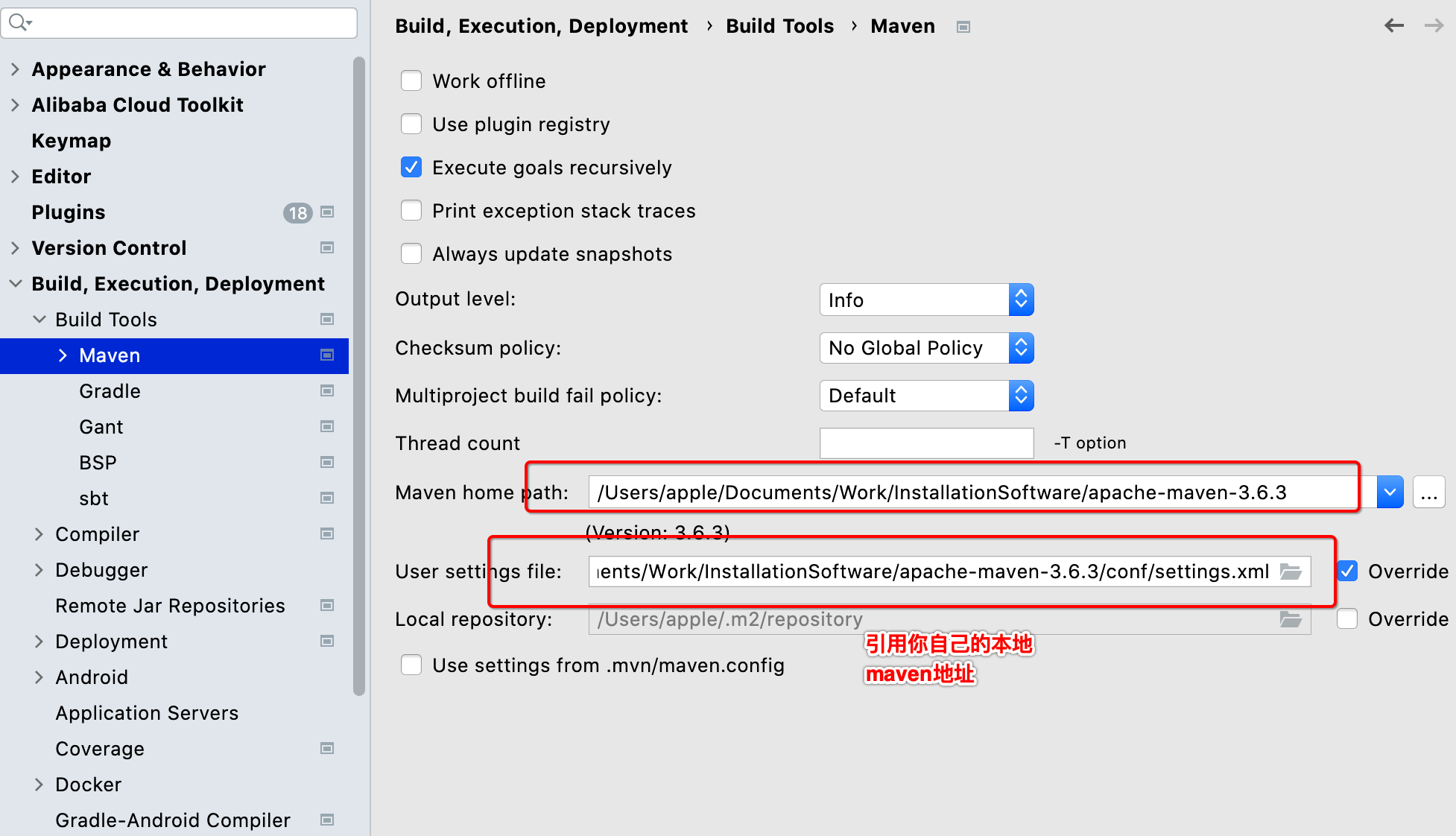
【Maven】Maven配置国内镜像
文章目录 1. 配置maven的settings.xml文件1.1. 先把镜像mirror配置好1.2. 再把仓库配置好 2. 在idea中引用3. 参考资料 网上配置maven国内镜像的文章很多,为什么选择我,原因是:一次配置得永生、仓库覆盖广、仓库覆盖全面、作者自用的配置。 1…...

ChatGPT有几个版本,哪个版本最强,如何选择适合自己的?
ChatGPT就像内容生产界的瑞士军刀。它可以是数学导师、治疗师、职业顾问、编程助手,甚至是旅行指南。只要你知道如何让它做你想做的事,ChatGPT几乎可以提供你要的任何东西。 但重要的是,你知道哪个版本的ChatGPT最能满足你的需求吗&#x…...

pg_standby备库搭建
1.主库 1.1主库参数文件修改 -- 该路径也需要在从库创建 mkdir -p /postgresql/archive chown -R postgres.postgres /postgresql/archive-- 主库配置归档 wal_levelreplica archive_modeon archive_commandcp %p /postgresql/archive/%f restore_commandcp /postgresql/arch…...
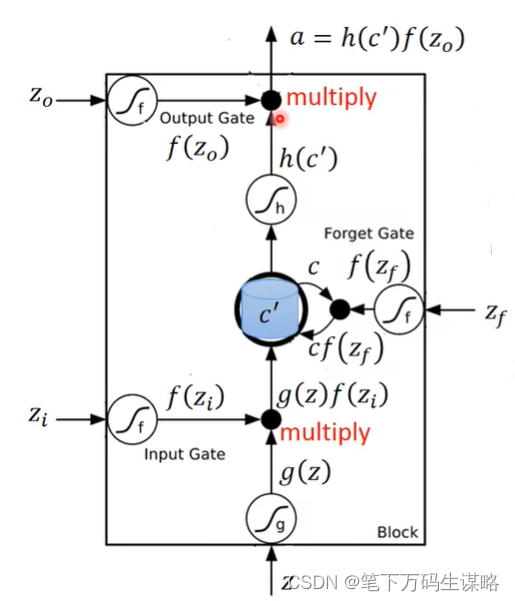
RNNLSTM
文章目录 前言引言应用示例-槽填充(slot filling)-订票系统二、循环神经网络(RNN)三、Long Short-term Memory (LSTM)LSTM原理[总结](https://zhuanlan.zhihu.com/p/42717426)LSTM例子lstm的训练RNN不但可以N2NMany2One(输入是一个矢量序列,但输出只有一个矢量)Many2Ma…...

到底什么是前后端分离
目录 Web 应用的开发主要有两种模式: 前后端不分离 前后端分离 总结 Web 应用的开发主要有两种模式: 前后端不分离 前后端分离 理解它们的区别有助于我们进行对应产品的测试工作。 前后端不分离 在早期,Web 应用开发主要采用前后端不…...
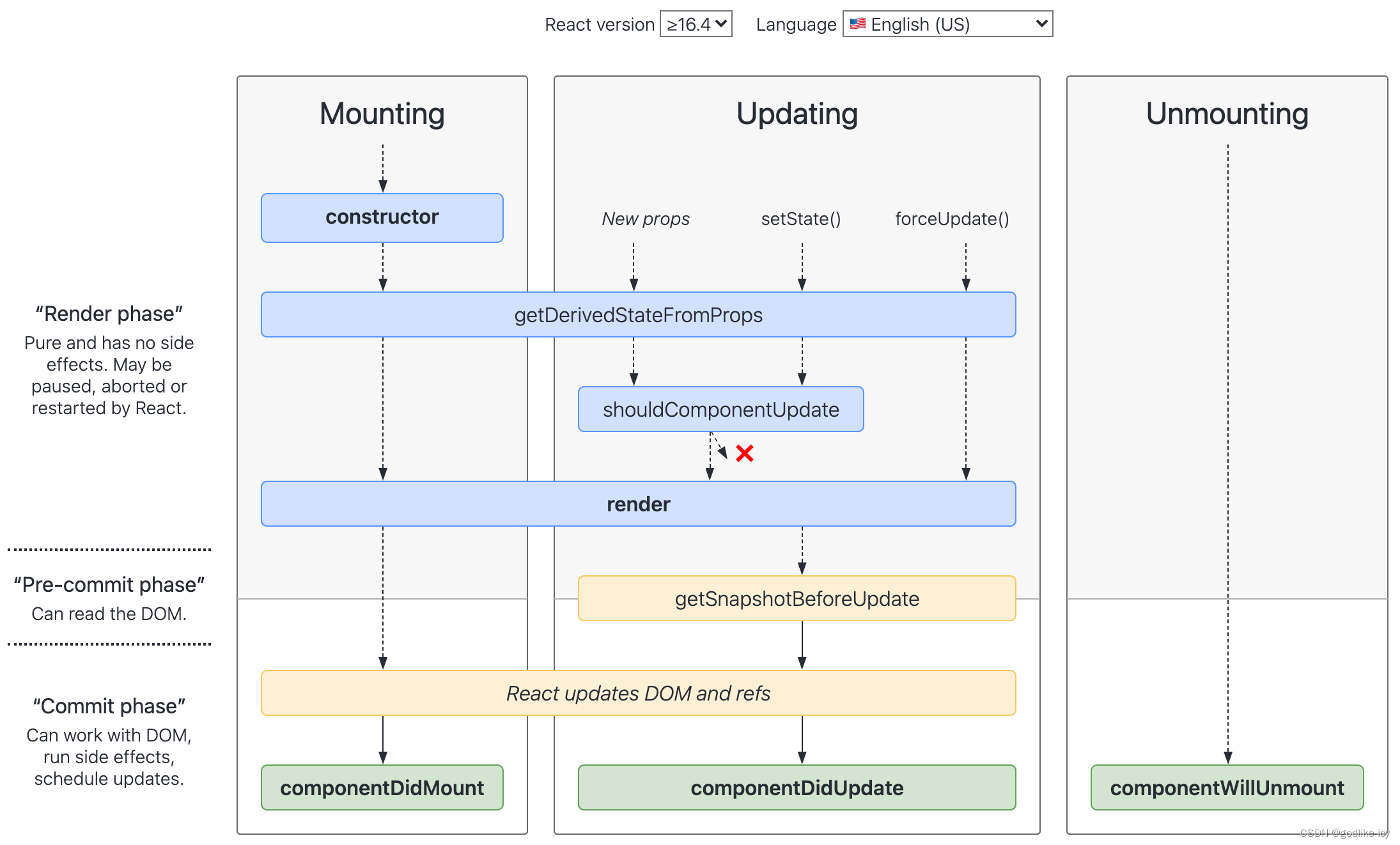
【React】精选5题
第1题:简述下 React 的生命周期?每个生命周期都做了什么? React 组件的生命周期可以分为三个阶段:挂载阶段、更新阶段和卸载阶段。每个生命周期方法都有特定的目的和功能。 挂载阶段: constructor:组件的构…...

MUR2080CT- ASEMI二极管的特性和应用
编辑-Z 本文将详细介绍MUR2080CT二极管的特性和应用。首先,将介绍MUR2080CT二极管的基本结构和工作原理。然后,将探讨MUR2080CT二极管的特性,包括正向电压降、反向漏电流和反向恢复时间等。接下来,将介绍MUR2080CT二极管在电源、…...

安全测试国家标准解读——资源管理和内存管理
下面的系列文章主要围绕《GB/T 38674—2020 信息安全技术 应用软件安全编程指南》进行讲解,该标准是2020年4月28日,由国家市场监督管理总局、国家标准化管理委员会发布,2020年11月01日开始实施。我们对该标准中一些常见的漏洞进行了梳理&…...

3D元宇宙游戏,或许能引爆新的文娱消费增长点
从去年开始,在互联网上,一个名为【神念无界-源起山海】的元宇宙游戏项目火了。除了可以在游戏内体验独战、团队式作战等3D古风经典游戏场景和玩法,还有钓鱼增加能量、情侣姻缘一线牵,结婚等多元化逼真效果与玩法,这令很…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...
