C++ | 红黑树以及map与set的封装
目录
前言
一、红黑树
1、红黑树的基本概念
2、红黑树相关特性
3、红黑树结点的定义
4、红黑树的查找
5、红黑树的插入
6、二叉树的拷贝构造与析构
7、红黑树的检测
8、红黑树总结
二、map与set的封装
1、红黑树的结点
2、红黑树迭代器
3、set的封装
4、map的封装
三、源码仓库
前言
前面我们讲过普通的二叉搜索树以及特殊的二叉搜索树 --- AVL树,今天,我们也要实现一种特殊的二叉搜索树,该树被广泛使用在STL库中的map与set的封装,这就是我们的 红黑树 ,怎么样,听名字就知道很霸气吧;本文就带着大家实现一个简单版本的红黑树以及用这个版本的红黑树对map与set进行封装;
一、红黑树
1、红黑树的基本概念
红黑树是二叉搜索树的一种,它与普通二叉搜索树不同之处是它有一些规则对其进行了限制,使其最长路径结点个数不会超出最短路径结点个数的两倍,下面我们就来看看红黑树相关特性;
2、红黑树相关特性
1、每个结点不是红色就是黑色
2、根节点是黑色的
3、如果一个节点是红色的,则它的两个孩子结点是黑色的(不会有连续的红色结点)
4、对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 、包含相同数目的黑色结点(每条路径上的黑色结点数量相同)
5、每个叶子结点都是黑色的(此处的叶子结点指的是空结点
思考:为什么满足以上特性,最长路径的结点个数不会超出最短路径节点个数的两倍呢?
根据上述5个条件,假设每条路径的黑色结点个数为3,那么最短路径应就是全是黑色结点,最长是黑红将间的路径结点;
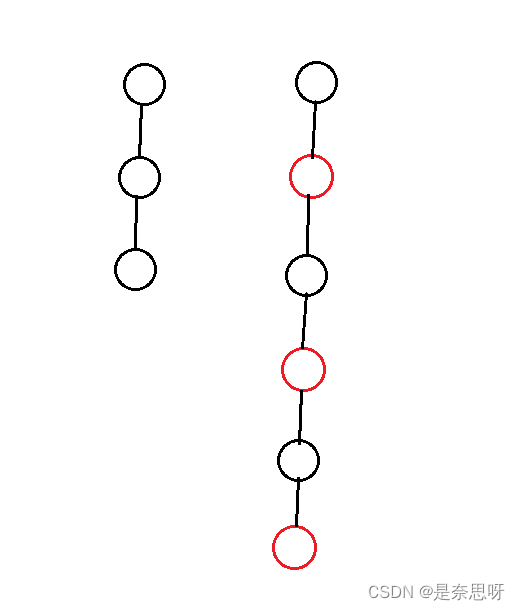
既然最长路径与最短路径我们都可以得到,根据上述,我们不难求证出最长路径的结点个数不会超出最短路径节点个数的两倍;
3、红黑树结点的定义
我们首先枚举出颜色,然后我们的红黑树结点用三叉链的方式进行连接,方便后续旋转调整;这里,其实有一个问题,我们构造的结点默认是红色还是黑色呢?
其实这个问题本质就是,对于新插入的结点,你更愿意违反规则3来进行调整,还是愿意违法规则4来进行后续的调整呢?答案是肯定的,当然愿意违反规则3,如果出现了连续的红色结点,我们可能仅仅只需要调整该红色结点所在子树;而违反规则4,我们需要调整整棵树,因为一颗树的黑色节点增多了,其他该所在路径也会增多,调整更麻烦;因此构造函数我们更愿意默认将结点置为红色;
enum Color{RED,BLACK};template<class K, class V>struct RBTreeNode{RBTreeNode(const std::pair<K, V> kv):_left(nullptr), _right(nullptr), _parent(nullptr), _color(RED), _kv(kv){}RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Color _color;std::pair<K, V> _kv;};4、红黑树的查找
红黑树的查找方式与普通二叉搜索树并无二异,这里就不做过多介绍了;此处顺便将红黑树的框架写出来了;
template<class K, class V>class RBTree{public:typedef RBTreeNode<K, V> Node;// 查找bool find(const K& key){if (_root == nullptr){return false;}Node* cur = _root;while (cur){if (key < cur->_kv.first){cur = cur->_left;}else if (key > cur->_kv.first){cur->_right;}else{// 找到了return true;}}return false;}private:Node* _root = nullptr;};5、红黑树的插入
红黑树的插入操作才是关键,也是本文讲解红黑树的核心;红黑树插入数据与以前的二叉搜索树插入数据的代码相同,主要是后面的调整操作,调整主要分为三种情况,我们先将插入逻辑的框架搭建起来,框架如下所示;
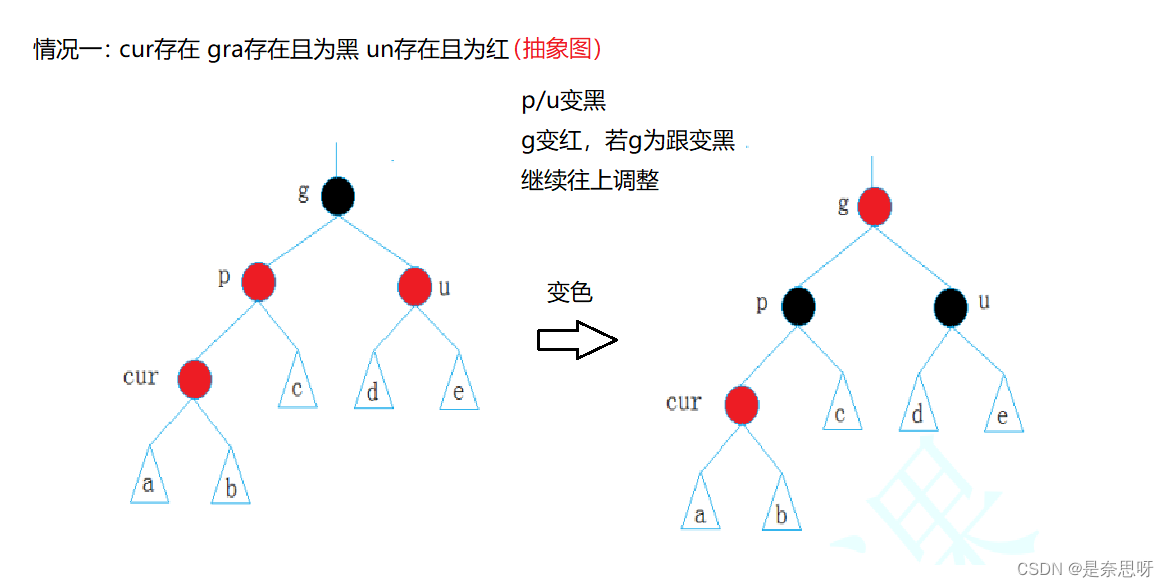
// 插入bool insert(const std::pair<K, V> kv){// 首次插入if (_root == nullptr){_root = new Node(kv);_root->_color = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{//有对应的key,返回falsereturn false;}}// 找到插入位置了,插入数据cur = new Node(kv);if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;// 以下为调整代码......暂未填充// .......return true;}接下来我带着大家逐步分析以下的三种情况;情况一是cur为红,parent为红,grandfather为黑,uncle为红,以下分别简称为c、p、g、u;
注意:我们举例三种情况均为parent为grandfather的左孩子,右孩子的情况与左孩子类似;
以下为具象图,这种情况可以一只沿着祖父往上调整,可能会调整几次,如下就调整了两次;
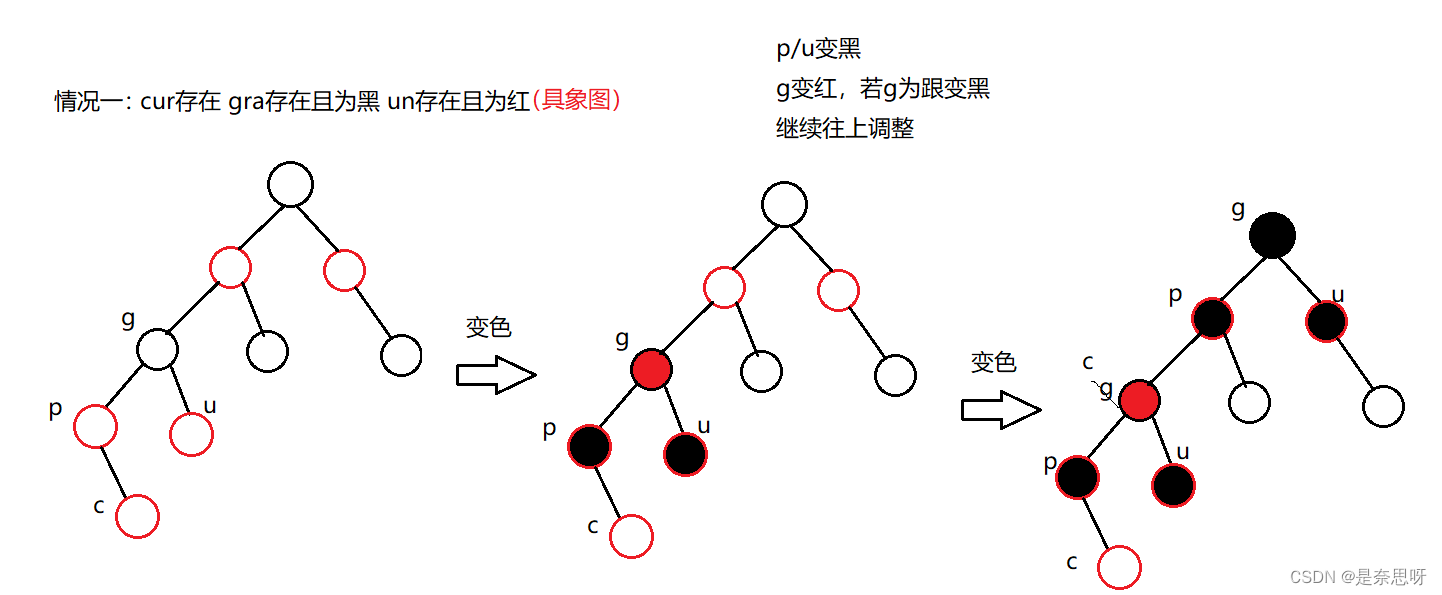
接着就是情况二,情况二看起来分为两种,实际就是一种情况,以下分别情况二的两种具象图;
注意:情况二调整完以后直接退出循环,无需继续往上调整;
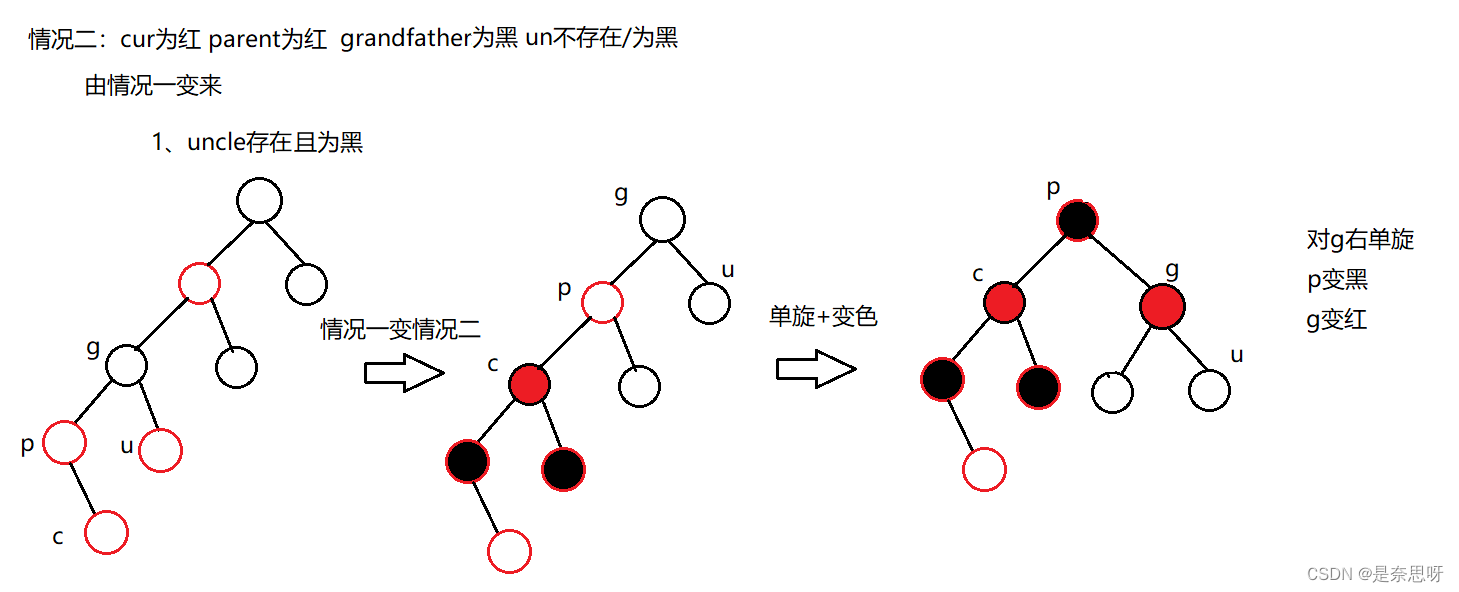
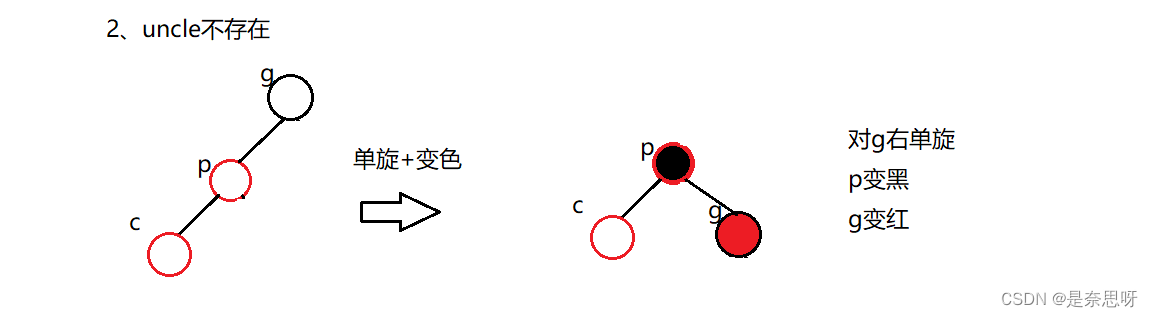
这里的右单旋就是我们前面AVL树的右单旋,代码也一模一样;如果parent是grandfather的左边就是左单旋,所以上面说我们进分析一边即可;
情况三实则是由情况一变成的,我们可以把情况三变成情况二,进行处理,因为cur的位置不同,而必须进行双旋;
注意:情况三调整完以后直接退出循环,无需继续往上调整;
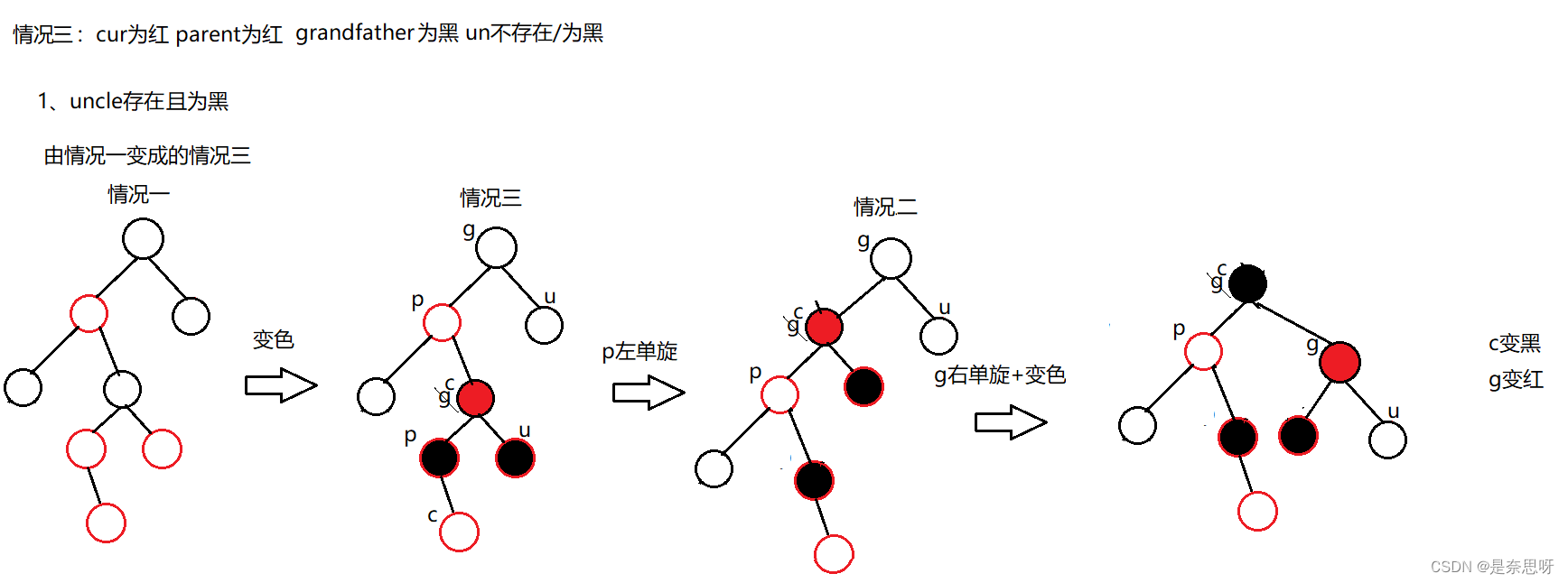
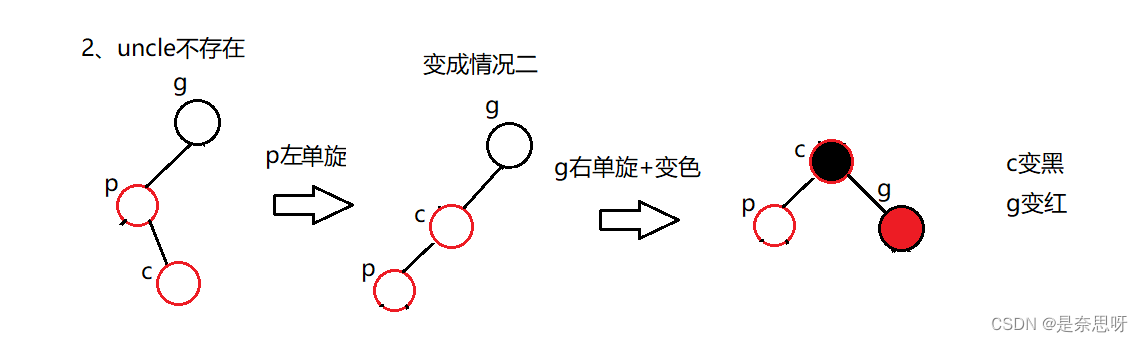
上述就是三种调整方式,我们根据上图可写出如下代码;
// 插入bool insert(const std::pair<K, V> kv){// 首次插入if (_root == nullptr){_root = new Node(kv);_root->_color = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{//有对应的key,返回falsereturn false;}}// 找到插入位置了,插入数据cur = new Node(kv);if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;// 调整while (parent && parent->_color == RED){// grandfather必然存在,不用判空,因为parent为红,不可能为根Node* grandfather = parent->_parent;if (grandfather->_left == parent){// 情况一 uncle 存在且为红Node* uncle = grandfather->_right;if (uncle && uncle->_color == RED){// 直接变色grandfather->_color = RED;parent->_color = BLACK;uncle->_color = BLACK;// 继续向上调整cur = grandfather;parent = cur->_parent;}else // 情况二 + 情况三{// 情况二if (parent->_left == cur){rotateR(grandfather);parent->_color = BLACK;grandfather->_color = RED;}else // 情况三{rotateL(parent);rotateR(grandfather);cur->_color = BLACK;grandfather->_color = RED;}break;}}else // grandfather->right == parent{Node* uncle = grandfather->_left;// 情况一if (uncle && uncle->_color == RED){// 变色parent->_color = BLACK;uncle->_color = BLACK;grandfather->_color = RED;// 继续像上调整cur = grandfather;parent = cur->_parent;}else // 情况二 + 情况三{// 情况二if (parent->_right == cur){rotateL(grandfather);grandfather->_color = RED;parent->_color = BLACK;}else{rotateR(parent);rotateL(grandfather);cur->_color = BLACK;grandfather->_color = RED;}break;}}// 上面可能会将root改为红色_root->_color = BLACK;}return true;}补充一下我们的旋转代码;
void rotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;// subRL挂在parent的右边parent->_right = subRL;if (subRL)subRL->_parent = parent;// 提前保存parent的父亲结点Node* pparent = parent->_parent;// parent挂到subR的左边subR->_left = parent;parent->_parent = subR;// 将subR与上层链接if (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = subR;subR->_parent = pparent;}else{pparent->_right = subR;subR->_parent = pparent;}}}void rotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;// 将subLR挂到parent的左边parent->_left = subLR;if (subLR)subLR->_parent = parent;// 提前保存parent的父亲结点Node* pparent = parent->_parent;// 将parent挂到subL的右边subL->_right = parent;parent->_parent = subL;// 将这颗子树的根结点与上面结点链接if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = subL;subL->_parent = pparent;}else{pparent->_right = subL;subL->_parent = pparent;}}}
6、二叉树的拷贝构造与析构
二叉树的拷贝构造我们通过先序的方式进行拷贝构造;
RBTree(const RBTree& rbt){if (this != &rbt){_root = _construction(rbt._root, nullptr);}}Node* _construction(Node* root, Node* parent){if (root == nullptr)return nullptr;Node* newroot = new Node(root->_val);newroot->_color = root->_color;newroot->_parent = parent;parent = newroot;newroot->_left = _construction(root->_left, parent);newroot->_right = _construction(root->_right, parent);return newroot;}二叉树的析构我们则需用类似后序遍历的方式进行逐个结点析构;
~RBTree(){destruction(_root);}void destruction(Node* root){if (root == nullptr)return;destruction(root->_left);destruction(root->_right);delete root;}7、红黑树的检测
前面代码我们完成了对红黑树的各种操作,现在我们来检测一下我们的红黑树是否为正确的红黑树;具体代码如下;
void inorder(){_inorder(_root);std::cout << std::endl;}bool is_balance(){if (_root->_color == RED)return false;int maxBlackNode = -1;return _is_balance(_root, 0, maxBlackNode);}int height(){return _height(_root);}int _height(Node* root){if (root == nullptr){return 0;}int left_height = _height(root->_left);int right_height = _height(root->_right);return left_height > right_height ? left_height + 1 : right_height + 1;}bool _is_balance(Node* root, int curBlackNode, int& maxBlackNode){if (root == nullptr){// 首次进入更新最大黑节点数量if (maxBlackNode == -1){maxBlackNode = curBlackNode;//cout << "黑色结点个数:" << maxBlackNode << endl;}if (curBlackNode != maxBlackNode){cout << "路径上的黑色结点数量不一致" << endl;return false;}//cout << curBlackNode << endl;return true;}if (root->_color == BLACK){curBlackNode++;}if (root->_color == RED && root->_parent->_color == RED){//cout << root->_parent->_kv.first << "颜色异常" << endl;return false;}return _is_balance(root->_left, curBlackNode, maxBlackNode) && _is_balance(root->_right, curBlackNode, maxBlackNode);}void _inorder(Node* root){if (root == nullptr)return;_inorder(root->_left);cout << KeyOfT()(root->_val) << " ";_inorder(root->_right);}我们可以通过如上的is_balance函数检测红黑树是否有误,如果还不放心我们可以通过如下代码进行测试;同时也对比了与AVL树的差别;
void test_RBTree2()
{srand((unsigned int)time(nullptr));const int N = 1000000;MySpace::RBTree<int, int> rb1;MySpace::AVLTree<int, int> avl1;for (int i = 0; i < N; i++){int num = rand() + i;rb1.insert(make_pair(num, num));avl1.insert(make_pair(num, num));}cout << "RB max height :" << rb1.height() << endl;cout << "RB is balance :" << rb1.is_balance() << endl;cout << "AVL max height :" << avl1.height() << endl;cout << "AVL is balance :" << avl1.is_balance() << endl;
}8、红黑树总结
有人发现我们红黑树并没有AVL树那样完全平衡,那么红黑树的意义是什么呢?实际上,我们的map与set都是使用红黑树来进行封装的,那么有的小伙伴就疑惑了,那么为什么不用AVL树进行封装呢?AVL树不是更加平衡,搜索效率更高么?实际上的确如此,搜索效率,有时候红黑树确实不如AVL树,可是我们不能但从查找来评判一棵树的好坏,我们的红黑树总体效率实际上要比我们的AVL树高的,因为我们的红黑树不是绝对平衡的,因此我们旋转的次数并不会有AVL树那么频繁,总体效率是比AVL树高的;
二、map与set的封装
实际上,我们的map与set仅仅只是套了一层红黑树的外壳接下来,我们稍稍修改上述的红黑树,对map与set完成封装;
1、红黑树的结点
这里的模板参数变成了T,当我们的set来的时候,传入的是Key,当我们的map来的时候传入的是pair<Key, Value>;
template<class T>struct RBTreeNode{RBTreeNode(const T& val):_left(nullptr), _right(nullptr), _parent(nullptr), _color(RED), _val(val){}RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;Color _color;T _val;};2、红黑树迭代器
我们要实现map与set的迭代器,就得先实现红黑树的迭代器;
template<class T, class Ref, class Ptr>struct RBTree_iterator{typedef RBTreeNode<T> Node;typedef RBTree_iterator<T, Ref, Ptr> Self;typedef RBTree_iterator<T, T&, T*> iterator;RBTree_iterator(Node* node):_node(node){}// 1、如果该类是普通迭代器,则作用为拷贝构造// 2、如果该类是const迭代器,则作用为用普通迭代器取构造const迭代器RBTree_iterator(const iterator& it):_node(it._node){}Ref operator*(){return _node->_val;}Ptr operator->(){return &_node->_val;}bool operator!=(const Self& it){return _node != it._node;}Self& operator++(){Node* cur = _node;if(cur){if (cur->_right != nullptr){// 右子树的最左节点cur = cur->_right;while (cur->_left){cur = cur->_left;}_node = cur;}else{// 找当前结点是父亲左结点的父亲Node* parent = cur->_parent;while (parent && parent->_right == cur){cur = parent;parent = parent->_parent;}_node = parent;}}return *this;}Self& operator--(){Node* cur = _node;if (cur){if (cur->_left != nullptr){// 左子树的最右结点Node* subR = cur->_left;while (subR->_right){subR = subR->_right;}_node = subR;}else{// 找当前结点是父亲的右节点的父亲Node* parent = cur->_parent;while (parent && parent->_left){parent = parent->_parent;}_node = parent;}}return *this;}Node* _node;};3、set的封装
接下来我们仅仅只需要将红黑树封装成set即可,直接套一层外壳;
template<class Key, class Value>struct SetKeyOfT{const Key& operator()(const Value& val){return val;}};template<class Key>class set{public:typedef Key key_type;typedef Key value_type;typedef RBTree<key_type, value_type, SetKeyOfT<key_type, value_type>> Tree;typedef typename RBTree<key_type, value_type, SetKeyOfT<key_type, value_type>>::const_iterator iterator;typedef typename RBTree<key_type, value_type, SetKeyOfT<key_type, value_type>>::const_iterator const_iterator;pair<iterator, bool> insert(const value_type& val){return _t.insert(val);}iterator begin(){return _t.begin();}iterator end(){return _t.end();}const_iterator begin() const{return _t.begin();}const_iterator end() const{return _t.end();}private:Tree _t;};解释一下这里的KeyOfT,这里只是一个仿函数,我们仅仅想通过这个取出Key值,因为红黑树的T也不确定是Key还是KeyValue模型;
注意:由于set的结点中的Key在树中不能被修改,因此这里set的普通迭代器和const迭代器都是红黑树的const迭代器;
4、map的封装
map的封装同样如此,我们仅仅只是套了一层红黑树的外壳;
template<class Key, class T>struct MapKeyOfT{const Key& operator()(const T& val){return val.first;}};template<class Key, class Value>class map{public:typedef Key key_type;typedef std::pair<Key, Value> value_type;typedef RBTree<const Key, value_type, MapKeyOfT<key_type, value_type>> Tree;typedef typename RBTree<const key_type, value_type, MapKeyOfT<key_type, value_type>>::iterator iterator;typedef typename RBTree<const key_type, value_type, MapKeyOfT<key_type, value_type>>::const_iterator const_iterator;iterator begin(){return _t.begin();}iterator end(){return _t.end();}const_iterator begin() const{return _t.begin();}const_iterator end() const{return _t.end();}std::pair<iterator, bool> insert(const value_type& val){return _t.insert(val);}private:Tree _t;};三、源码仓库
关于红黑树、map与set的所有源码小编都放进代码仓库中供大家参考;以下为源码仓库;
源码仓库
相关文章:

C++ | 红黑树以及map与set的封装
目录 前言 一、红黑树 1、红黑树的基本概念 2、红黑树相关特性 3、红黑树结点的定义 4、红黑树的查找 5、红黑树的插入 6、二叉树的拷贝构造与析构 7、红黑树的检测 8、红黑树总结 二、map与set的封装 1、红黑树的结点 2、红黑树迭代器 3、set的封装 4、map的封…...

逻辑斯特回归
*分类是离散的,回归是连续的 下载数据集 trainTrue:下载训练集 逻辑斯蒂函数保证输出值在0-1之间 能够把实数值映射到0-1之间 导函数类似正态分布 其他饱和函数sigmoid functions 循环神经网络经常使用tanh函数 与线性回归区别 塞戈马无参数&#x…...

OpenCV 算法解析
opencv大坑之BGR opencv对于读进来的图片的通道排列是BGR,而不是主流的RGB!谨记! #opencv读入的矩阵是BGR,如果想转为RGB,可以这么转 img4 cv2.imread(1.jpg) img4 cv2.cvtColor(img4,cv2.COLOR_BGR2RGB) OpenCV 常见…...

springboot创建并配置环境(一) - 创建环境
文章目录 一、介绍二、启动环境Environment的分析三、进入源码四、创建环境1. 如何确定应用类型2. 测试 一、介绍 在springboot的启动流程中,启动环境Environment是可以说是除了应用上下文ApplicationContext之外最重要的一个组件了,而且启动环境为应用…...

2023JAVA 架构师面试 130 题含答案:JVM+spring+ 分布式 + 并发编程》...
此文包含 Java 面试的各个方面,史上最全,苦心整理最全 Java 面试题目整理包括基JVM算法数据库优化算法数据结构分布式并发编程缓存等,使用层面广,知识量大,涉及你的知识盲点。要想在面试者中出类拔萃就要比人付出更多的…...
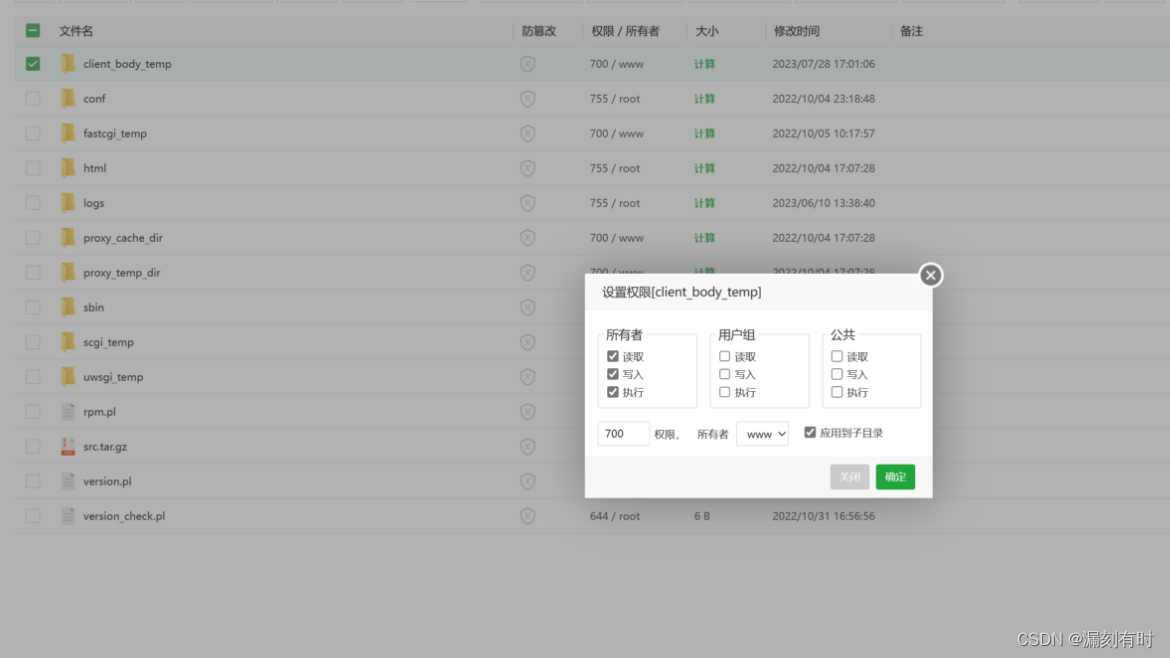
layui手机端上传文件时返回404 Not Found的解决方案(client_body_temp权限设置)
关于 1.client_body_temp的作用 client_body_temp是一个指令指定保存客户端请求体临时文件的目录路径,以及是否进行缓存的配置指令。 在Web服务器中,当客户端向服务器发送请求时,请求体中包含了请求的主体部分,比如表单数据、上…...

网络编程知识
网络编程知识 一.网络七层模型 OSI模型: OSI 模型(Open System Interconnection model)是一个由国际标准化组织􏰁提出的概念模型,试图提供一个使各种不同的计算机和网络在世界范围内实现互联的标准框架。它将计算机网络体系结构划分为七层…...
线性神经网路——线性回归随笔【深度学习】【PyTorch】【d2l】
文章目录 3.1、线性回归3.1.1、PyTorch 从零实现线性回归3.1.2、简单实现线性回归 3.1、线性回归 线性回归是显式解,深度学习中绝大多数遇到的都是隐式解。 3.1.1、PyTorch 从零实现线性回归 %matplotlib inline import random import torch #d2l库中的torch模块&a…...

js实现多种按钮
你可以使用JavaScript来实现多种类型的按钮,以下是几个常见的示例: 普通按钮(Normal Button): <button>Click me</button> 带图标的按钮(Button with Icon): <bu…...
)
getopt函数(未更新完)
2023年7月28日,周五上午 这是我目前碰到过的比较复杂的函数之一, 为了彻底弄懂这个函数,我花了几个小时。 为了更好的说明这个函数,之后我可能会录制讲解视频并上传到B站, 如果我上传到B站,我会在文章添…...
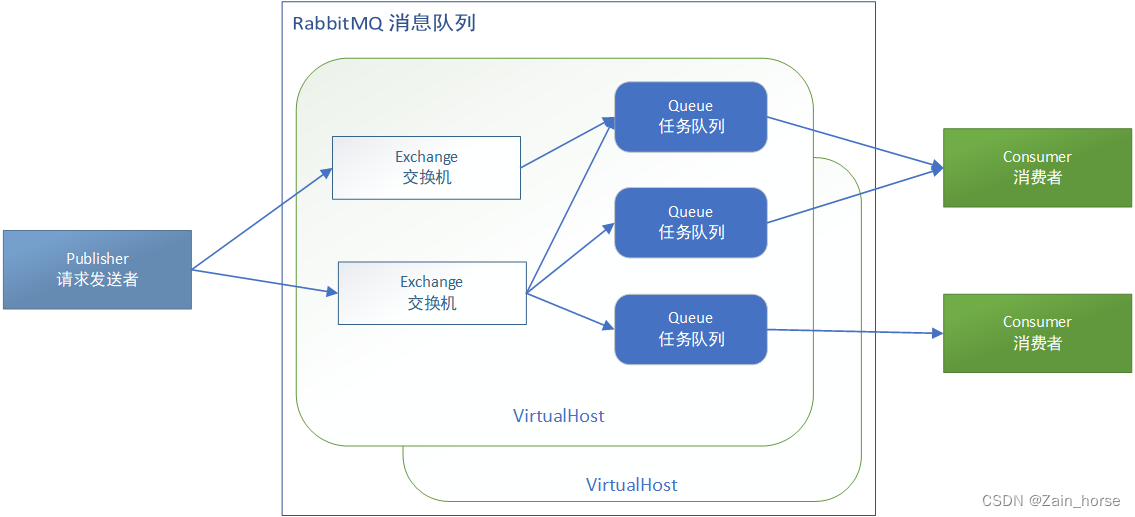
SpringCloud学习路线(9)——服务异步通讯RabbitMQ
一、初见MQ (一)什么是MQ? MQ(MessageQueue),意思是消息队列,也就是事件驱动架构中的Broker。 (二)同步调用 1、概念: 同步调用是指,某一服务…...
postcss-pxtorem适配插件动态配置rootValue(根据文件路径名称,动态改变vue.config里配置的值)
项目背景:一个项目里有两个分辨率的设计稿(1920和2400),不能拆开来打包 参考: 是参考vant插件:移动端Vant组件库rem适配下大小异常的解决方案:https://github.com/youzan/vant/issues/1181 说明: 因为vue.c…...

代码随想录算法训练营第二十三天 | 额外题目系列
额外题目 1365. 有多少小于当前数字的数字借着本题,学习一下各种排序未看解答自己编写的青春版重点代码随想录的代码我的代码(当天晚上理解后自己编写) 941.有效的山脉数组未看解答自己编写的青春版重点代码随想录的代码我的代码(当天晚上理解后自己编写) 1207. 独一…...

UiAutomator
运行Espresso和UI Automator测试时要使用模拟器。国内手机的ROM大多进行过修改,可能加入很多限制,导致测试无法正常运行。 Espresso只支持一个活动内部交互行为的测试。跨越多个活动、多个应用的场景需要使用UI Automator。使用Espresso和UI Automator的…...

stm32标准库开发常用函数的使用和代码说明
文章目录 GPIO(General Purpose Input/Output)NVIC(Nested Vectored Interrupt Controller)DMA(Direct Memory Access)USART(Universal Synchronous/Asynchronous Receiver/Transmitter…...

有关合泰BA45F5260中断的思考
最近看前辈写的代码,发现这样一段代码: #ifdef SUPPORT_RF_NET_FUNCTION if(UART_INT_is_L()) { TmrInsertTimer(eTmrHdlUartRxDelay,TMR_PERIOD(2000),NULL); break; } #endif 其中UART_INT_is_L&am…...

Numpy-算数函数与数学函数
⛳算数函数 如果参与运算的两个对象都是ndarray,并且形状相同,那么会对位彼此之间进 第 30 页 行( - * /)运算。NumPy 算术函数包含简单的加减乘除: add(),subtract(),multiply() 和divide()。 …...

Nginx在springboot中起到的作用
面试时这样回答: 在Spring Boot项目中使用Nginx可以有以下用途: 1. 反向代理:Nginx可以作为反向代理服务器,将外部请求转发到后端的Spring Boot应用,并可以实现负载均衡、高可用、缓存等功能,提高系统的性…...

12.(开发工具篇vscode+git)vscode 不能识别npm命令
1:vscode 不能识别npm命令 问题描述: 解决方式: (1)右击VSCode图标,选择以管理员身份运行; (2)在终端中执行get-ExecutionPolicy,显示Restrictedÿ…...

如何在MacBook上彻底删除mysql
好久以前安装过,但是现在配置mysql一直出错,索性全部删掉重新配置。 一、停止MySQL服务 首先,请确保 MySQL 服务器已经停止运行,以免影响后续的删除操作。 sudo /usr/local/mysql/support-files/mysql.server stop如果你输入之…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...
