vue Can‘t resolve ‘path‘
BREAKING CHANGE: webpack < 5 used to include polyfills for node.js core modules by default.
This is no longer the case. Verify if you need this module and configure a polyfill for it.
这句话的意思是webpack 5之前是自动导入node一些核心模块的垫片,现在不导入了,你自己的导入吧!
第一步:
npm i -D path-browserify
第二步(在route.js):
改成:import path from 'path-browserify'
或者:在vue.config.js里面修改
config.resolve.alias.set('path', require.resolve('path-browserify'))
相关文章:

vue Can‘t resolve ‘path‘
BREAKING CHANGE: webpack < 5 used to include polyfills for node.js core modules by default. This is no longer the case. Verify if you need this module and configure a polyfill for it. 这句话的意思是webpack 5之前是自动导入node一些核心模块的垫片…...

【JavaEE初阶】——第七节.Servlet入门学习笔记
作者简介:大家好,我是未央; 博客首页:未央.303 系列专栏:JavaEE进阶 每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!! 文章目录 前…...
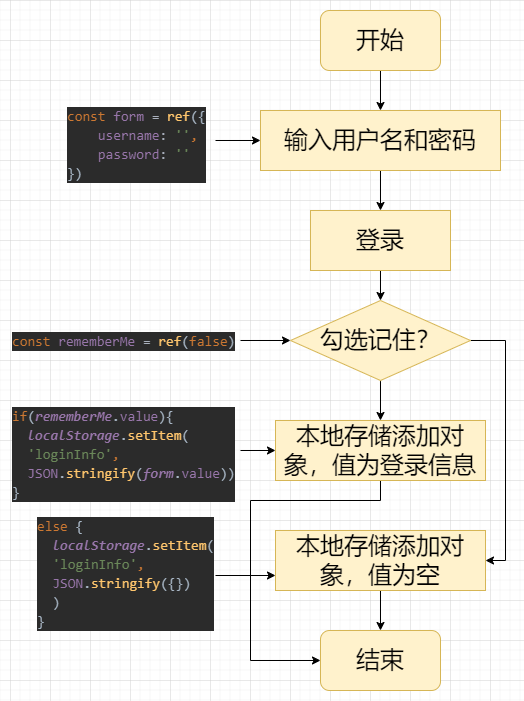
vue项目登录页面实现记住用户名和密码
vue项目登录页面实现记住用户名和密码 记录一下实现的逻辑,应该分两步来理解这个逻辑 首次登录,页面没有用户的登录信息,实现逻辑如下: 用户输入用户名和密码登录,用户信息为名为form的响应式对象,v-model…...
数学建模-MATLAB三维作图
导出图片用无压缩tif会更清晰 帮助文档:doc 函数名 matlab代码导出为PDF 新建实时脚本或右键文件转换为实时脚本实时编辑器-全部运行-内嵌显示保存为PDF...

pytorch工具——使用pytorch构建一个神经网络
目录 构建模型模型中的可训练参数假设输入尺寸为32*32损失函数反向传播更新网络参数 构建模型 import torch import torch.nn as nn import torch.nn.functional as Fclass Net(nn.Module):def __init__(self):super(Net,self).__init__()#定义第一层卷积层,输入维…...
)
在CSDN学Golang云原生(Kubernetes Pod)
一,pod的定义与基本用法 在 Kubernetes 中,Pod 是最小的可部署单元,它包含一个或多个容器。使用 Golang 来定义和操作 Pod 时,需要使用 kubernetes/client-go 包提供的 API。 以下是 Golang 定义和基本用法 Pod 的示例ÿ…...

我开源了团队内部基于SpringBoot Web快速开发的API脚手架v1.7.0更新
什么是 rest-api-spring-boot-starter rest-api-spring-boot-starter 适用于SpringBoot Web API 快速构建让开发人员快速构建统一规范的业务RestFull API 不在去关心一些繁琐。重复工作,而是把重点聚焦到业务。 动机 每次Web API常用功能都需要重新写一遍。或者复…...
excel要如何自动累加某个单元格上方的所有单元格?
输入公式 SUM(INDIRECT("A1:A"&ROW()-1)) 运行实例如下图 注意图中b4,和b5单元格都输入相同的公式。 此方法可以避免写vba,以前此类问题的解决都是通过vba代码进行处理 对函数进行解析 主要使用了 INDIRECT() 2、公式说明:…...

广州道可维斯受邀参加首届金蝶暨佛山数字化生态峰会
2023首届金蝶暨佛山数字化生态峰会,于7月28日在佛山隆重举行。此次大会由金蝶软件集团主办,共有超150家软件行业企业莅临参与,共同探讨数字化行业的最新动态和趋势。 活动当日,道可维斯的客户成功中心主任梁健,做了以“企业内容管…...

ubuntu远程控制小车 运行rviz时报错
我买的是wheeltec的小车,测试rgbd相机时想在ubuntu上的rviz中显示小车的姿态和看到的rgb和depth图,但是ubuntu中rostopic list和rviz都找不到小车发布的话题信息,运行rqt_image_view时可以显示图片信息。 最终wheeltec的技术人员lucas帮我找了…...

轻松实现自定义数据脱敏返回
学习目标: 实现简单的数据脱敏功能 例如: 学习自定义数据脱敏 学习内容: 使用到:泛型、反射 /*** * param obj 需要数据脱敏的对象* param par 那些字段需要脱敏* param <T>* return* throws Exception*/public static …...
函数)
pytorch 中_call_impl()函数
记录pytorch 版本中的 nn.Module() 重要函数 1. _call_impl() 1.1 torch1.7.1 版本 def _call_impl(self, *input, **kwargs):for hook in itertools.chain(_global_forward_pre_hooks.values(),self._forward_pre_hooks.values()):result hook(self, input)if result is n…...

openGauss学习笔记-22 openGauss 简单数据管理-HAVING子句
文章目录 openGauss学习笔记-22 openGauss 简单数据管理-HAVING子句22.1 语法格式22.2 参数说明22.3 示例 openGauss学习笔记-22 openGauss 简单数据管理-HAVING子句 HAVING子句可以让我们筛选分组后的各组数据。 WHERE子句在所选列上设置条件,而HAVING子句则在由…...
干货 | 常见电路板GND与外壳GND之间接一个电阻一个电容,为什么?
干货 | 常见电路板GND与外壳GND之间接一个电阻一个电容,为什么? 外壳是金属的,中间是一个螺丝孔,也就是跟大地连接起来了。这里通过一个1M的电阻跟一个0.1uF的电容并联,跟电路板的地连接在一起,这样有什么好…...

网络层协议总览
网络层协议总览 IPARP(地址解析协议)ICMP(网际控制报文协议)路由选择协议NAT(网络地址转换协议) 网络层的主要协议包括IP、ARP、RARP、ICMP、IGMP以及各种路由选择协议等。 IP IP协议是TCP/IP协议簇中的核…...

C++模拟实现list
1.首先要了解到vs底层的list链表是带头双向循环的链表。 所以首先就要看成员变量 那么就说明我们还需要构造一个Node的结构体,(typedef一下就好了,名字不影响) 现在就可以完成间的push_back函数了。 1.list的iterator 我们之前模…...

PostgreSQL PG16 逻辑复制在STANDBY 上工作 (译)
开头还是介绍一下群,如果感兴趣polardb ,mongodb ,mysql ,postgresql ,redis 等有问题,有需求都可以加群群内有各大数据库行业大咖,CTO,可以解决你的问题。加群请联系 liuaustin3 ,在新加的朋友会分到2群(共…...

《零基础入门学习Python》第058讲:论一只爬虫的自我修养6:正则表达式2
上一节课我们通过一个例子(匹配 ip 地址)让大家初步了解到正则表达式的魔力,也让大家充分了解到学习正则表达式是一个相对比较困难的事情。所以这一节课我们将继续学习 正则表达式的语法。 我们依稀还记得在Python中,正则表达式是…...
第一堂棒球课:MLB棒球大联盟的主要战术·棒球1号位
MLB棒球大联盟的主要战术 攻击战术run-and-foul(跑垒战术):以速度为优势,在适当的时机发动进攻,争取在一回合内完成得分。 grounder(阻截战术):队员在垒包之间阻止对手的跑垒和传球。…...

【论文阅读】利用道路目标特征的多期车载激光点云配准
目录 引 言1 道路场景点云特征2 配准方法2.1 配准基元获取2.2 特征点提取2.3 两期道路场景车载点云的配准 2.3.1 基于特征点的4PCS 粗配准 3 实验与分析4 结论5 参考文献 摘 要 针对车载移动测量系统获取的城市道路点云场景巨大、目标复杂多样,多期道路场景重访车载…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
