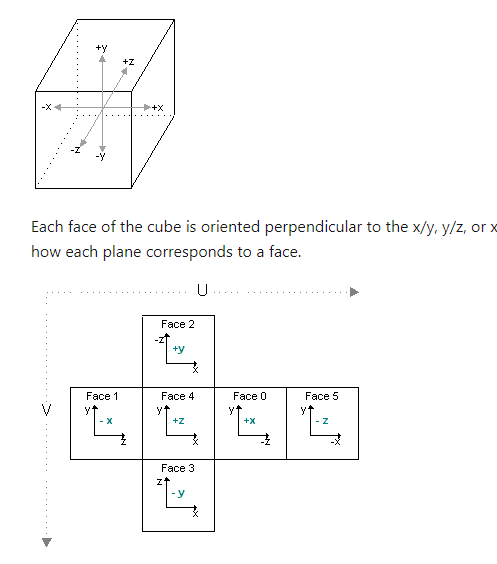
2.3 HLSL常用函数
一、函数介绍
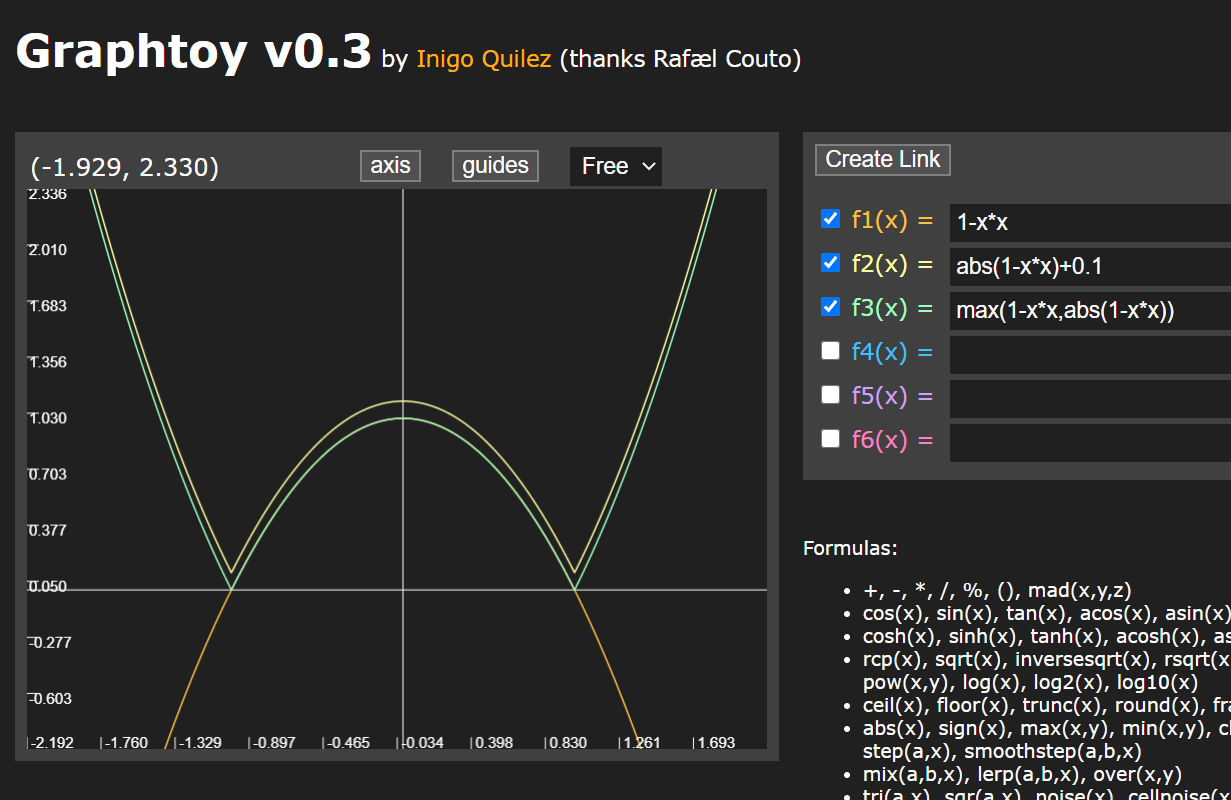
函数图像参考网站:Graphtoy
1.基本数学运算
| 函数 | 含义 | 示例图 |
| min(a,b) | 返回a、b中较小的数值 | |
| mul(a,b) | 两数相乘用于矩阵计算 | |
| max(a,b) | 返回a、b中较大的数值 |
|
| abs(a) | 返回a的绝对值 | |
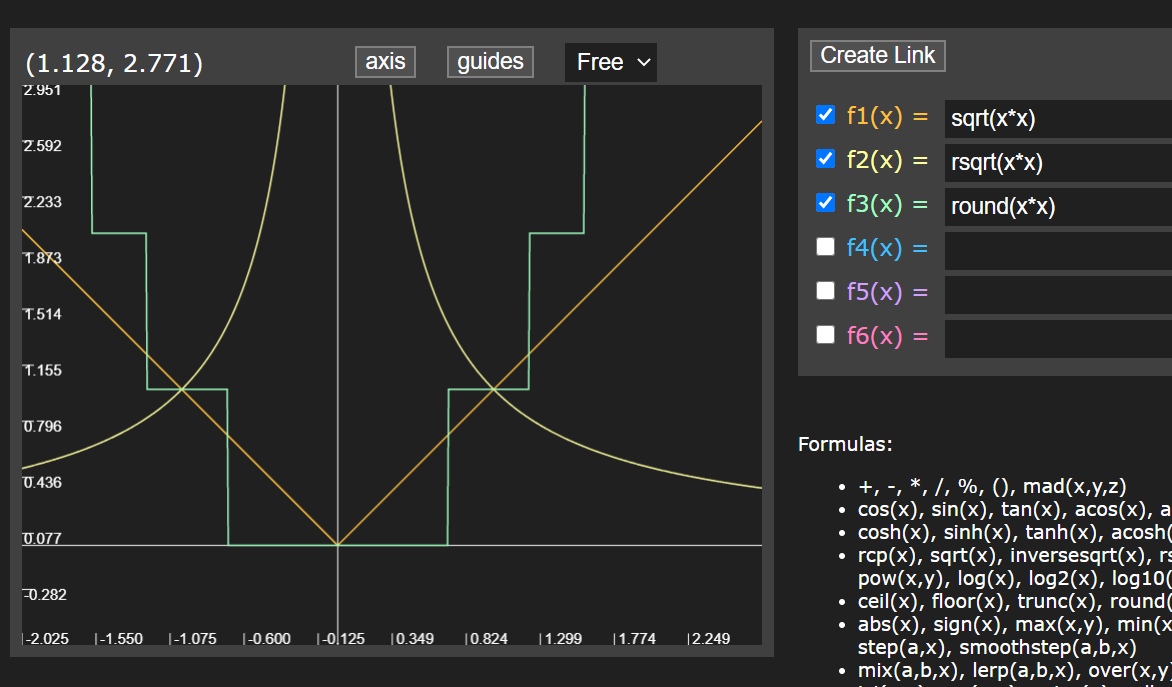
| round(x) | 返回与x最近的整数 |
|
| sqrt(x) | 返回x的平方根 | |
| rsqrt(x) | 返回x平方根的倒数 | |
| degregee(x) | 转换成弧度 | |
| redians(x) | 将角度转为弧度制 | |
| noise(x) | 噪声函数 |
2.幂指对与偏导数
| 函数 | 含义 | 示例图 |
| pow(x,y) | x的y次幂,xy |
|
| ldexp(x,exp) | 返回x与2的exp次方的乘积,x*2exp | |
| exp(x) | 返回以e为底的指数函数,ex | |
| exp2(x) | 返回以2为底的指数函数,2x | |
| log(x) | 返回x以e为底的对数,lnx | |
| log10(x) | 求以10为底的对数,log10x | |
| log2(x) | 求以2为底的对数,log2x | |
| frexp(x,out exp) | 把一个浮点数分解为尾数和指数, x : 要分解的浮点数据 返回值: 返回尾数 x = 尾数*2指数 (如果x参数为0,则此函数的尾数和指数均返回0) |
3.三角函数与双曲线函数
| 函数 | 含义 | 示例图 |
| sin(x) | 返回x的正弦值 | |
| cos(x) | 返回x的余弦值 | |
| tan(x) | 返回x的正切值 | |
| tan(y,x) | 返回y/x的正切值 | |
| sincos(x, out s, out c) | 返回x的正弦和余弦值 | |
| asin(x) | 返回x的反正弦值 |
|
| acos(x) | 返回x的反余弦值 | |
| atan(x) | 返回x的反正切值 | |
| atan2(y,x) | 返回y/x的反正切值 | |
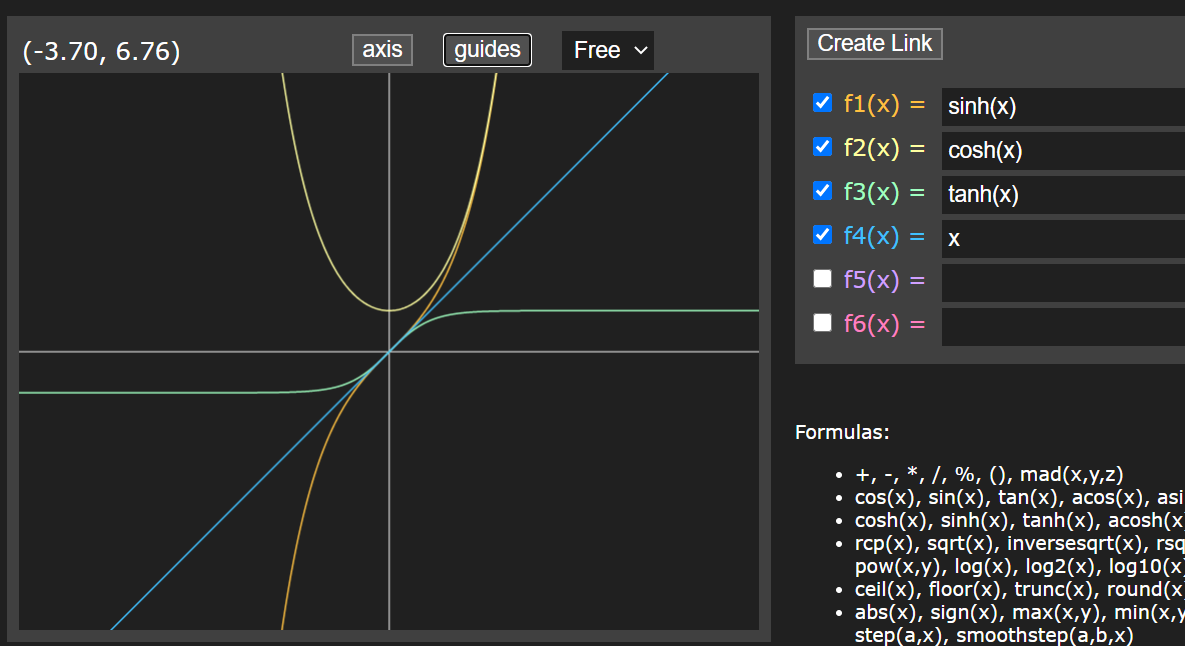
| sinh(x) | 返回x的双曲正弦值,0.5*(ex-e-x) |
|
| cosh(x) | 返回x的双曲余弦值 0.5*(ex-e-x) | |
| tanh(x) | 返回x的双曲正切值 |
4.数据范围
| 函数 | 含义 | 示例图 |
| ceil(x) | 返回>=x的最小整数 |
|
| step(x,y) | x<=y为1,否则为0 | |
| floor(x) | 返回小于或等于x的最大整数 | |
| saturate(x) | 返回将x限制在0和1之间的值 | |
| clamp(x,min,max) | 把x限制在[min,max]范围内,小于返回min,大于返回max | |
| frac(x) | 返回x的小数部分 | |
| fmord(a,b) | 返回a/b的浮点部分 | |
| modf(x,out ip) | 将值x分为小数和整数部分(各部分符号与x相同),ip返回整数部分,整体返回小数部分 | |
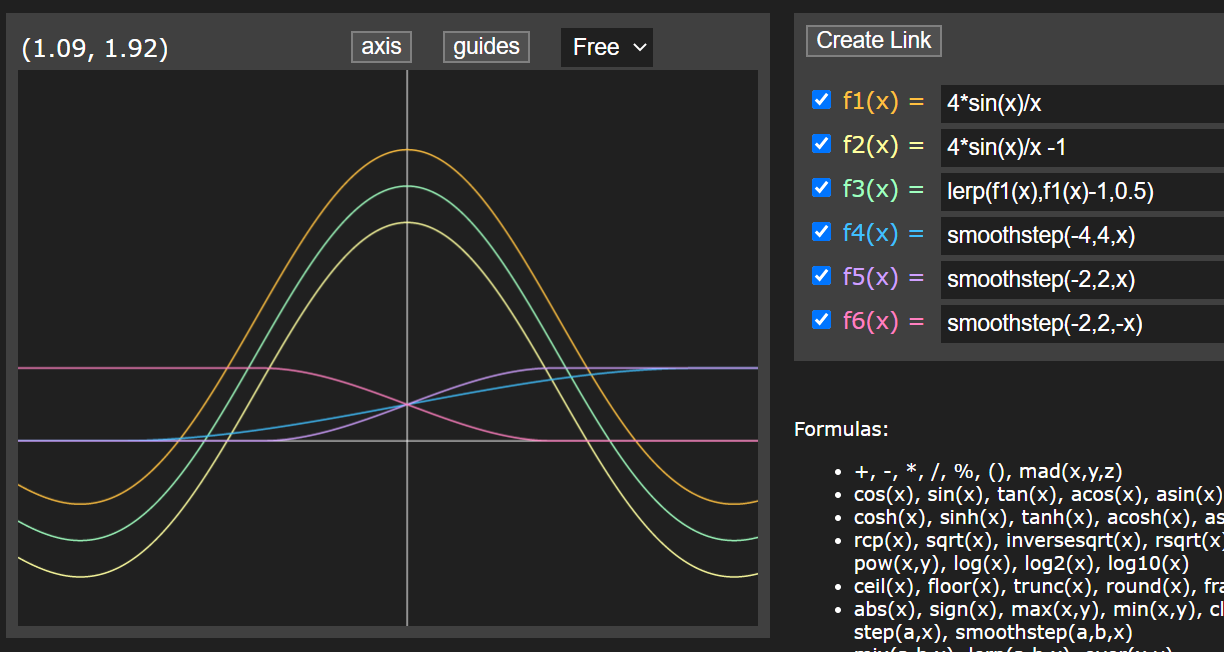
| lerp(a,b,s) | 按照s在a到b之间差值 |
|
| smoothstep(min,max,x) | 如果x在[min,max]范围内,则返回介于0~1之间的平滑Hermite差值;使用smoothstep HLSL内在函数在两个值之间创建平滑过渡。例如,使用此功能平滑的混合两种颜色 |
5.类型判断类
| 函数 | 含义 |
| all(x) | 确定指定量的所有分量是否均为非零,均非零则返回true,否则返回false(处理由浮点、整形、布尔型数据定义的标量,向量或者矩阵) |
| clip(x) | 如果输入值小于0,则丢弃当前像素,常用语判定范围(不仅仅针对0,返回值为void),常用于测试alpha,如果每个分量代表到平面的距离,还可以用来模拟剪切平面 |
| sign(x) | 返回x的正负性,如果x小于0返回-1,如果x等于0返回0,如果x大于0返回1 |
| isinf(x) | 如果x参数为+INF或者-INF(无穷+无穷仍无穷,0x3f3f3f3f),返回true,否则返回false |
| isfinite(x) | 判断x参数是有有界,有限的,与isinf(x)相反 |
| isnan(x) | 如果x参数为NAN(非数字),返回true,否则返回false |
6.向量与矩阵类
| 函数 | 含义 |
| length(v) | 返回向量的长度 |
| normalize(v) | 向量归一化,x/length(x) 方向向量归一化 |
| distance(a,b) | 返回两个向量之间的距离,按理说应该为0,此处表示为根号下各分量之差的平方和 |
| dot(a,b) | 返回a和b这两个向量的标积/内积/数量积/点积(a在b上的投影长,a·b=|a||b|·cosθ) |
| cross(a,b) | 返回a和b这两个向量的矢积/外积/向量积/叉积(返回值是个向量,而且与a、b都垂直,大小上|a×b| = |a| * |b| * sinθ) |
| determinant(m) | 返回指定浮点矩阵的按行列方式计算的值 |
| transpose(m) | 返回矩阵m的转置矩阵 |
7.光线运算类
| 函数 | 含义 | 示例图 |
| reflect(i, n) | 返回以i为入射向量n为法线方向的反射光 |
|
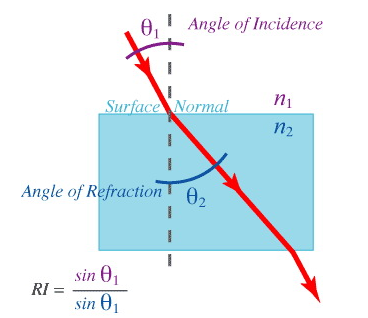
| refract(i, n, ri) | 返回以i为入射向量n为返现方向,ri为折射率的折射光 | |
| lit(n_dot_l, n_dot_h, m) | 输入标量(normal,light,半角向量h,镜面反射系数m),返回光照向量(环境光,漫反射光,镜面高光反射,1) | |
| faceforward(n, i, ng) | 得到面向视图方向的曲面法向量,输入输出为同源向量,返回 -n*sign(dot(i,ng))(normal,light,normal) |
8.1D纹理查找(几乎不会使用)
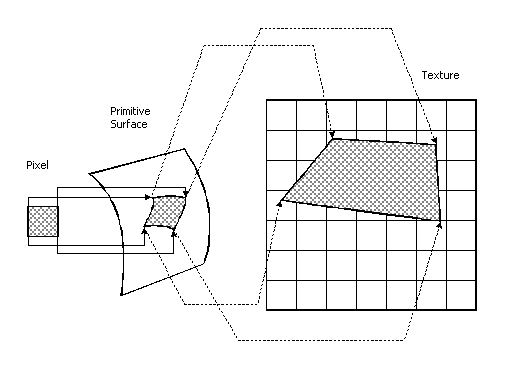
GPU在PS阶段是在屏幕空间XY坐标系中对每一个像素去对应的文立中查找对应的纹素确定像素的颜色。
《GPU 编程与CG语言之阳春白雪下里巴人》
| 函数 | 含义 | |
| tex1D(s,t) | 普通一维纹理查找,返回纹理采样器s在标量t位置的color4 | |
| tex1D(s,t,ddx,ddy) | 使用微分查询一维纹理t和ddxy均为vector | |
| tex1Dlod(s,t) | 使用LOD查找纹理s在t.w位置的color4 | |
| tex1Dbias(s,t) | 将t.w决定的某个MIP层偏置后的一维纹理查找 | |
| tex1Dgrad(s,t,ddx,ddy) | 使用微分并制定MIP层的一维纹理查找 | |
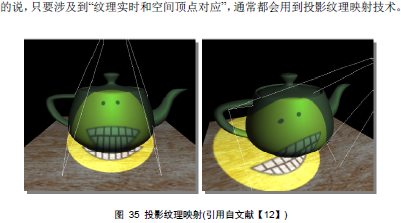
| tex1Dproj(s,t) | 把纹理当做一张幻灯片投影到场景中,先试用投影纹理技术需要计算出投影纹理坐标t(坐标t.w除以透视值),然后使用投影纹理坐标进行查询 |
|


9.2D纹理查找
| 函数 | 含义 | 示例图 |
| tex2D(s,t) | 普通二维纹理查找,返回纹理采样器s在vector t位置的颜色 | |
| tex2D(s,t,ddx,ddy) | 使用微分查询二维纹理 t和ddxy均为vector | |
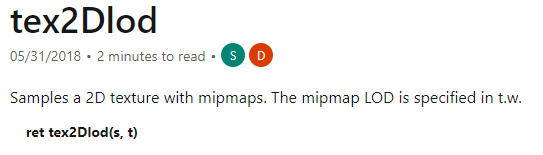
| tex2Dlod(s,t) | 使用LOD查找纹理s在t.w位置的color4 |
|
| tex2Dbias(s,t) | 将t.w决定的某个MIP层偏置后的二维纹理查找 |
|
| tex2Dgrad(s,t,ddx,ddy) | 使用微分并指定MIP层的二维纹理查找 |
|
| tex2Dproj(s,t) | 把纹理当做一张幻灯片投影到场景中,先使用投影纹理技术需要计算出投影纹理坐标t(坐标t.w除以透视值),然后使用投影纹理坐标进行查询 |
10.3D纹理查找
| 函数 | 含义 | 示例图 |
| tex3D(s,t) | 普通三维纹理查找,返回纹理采样器s在vector t位置的颜色 |
|
| tex3D(s,t,ddx,ddy) | 使用微分查询三维纹理 t和ddxy均为vector | |
| tex3Dlod(s,t) | 使用LOD查找纹理s在t.w位置的color4 | |
| tex3Dbias(s,t) | 将t.w决定的某个MIP层偏置后的三维纹理查找 | |
| tex3Dgrad(s,t,ddx,ddy) | 使用微分并指定MIP层的三维纹理查找 | |
| tex3Dproj(s,t) | 把纹理当做一张幻灯片投影到场景中,先使用投影纹理技术需要计算出投影纹理坐标t(坐标t.w除以透视值),然后使用投影纹理坐标进行查询 |
11.立体纹理查找
| 函数 | 含义 | 示例图 |
| texCUBE(s,t) | 返回纹理采样器s在vector t位置的颜色 |
|
| texCUBE(s,t,ddx,ddy) | 使用微分查询一维纹理t和ddxy均为vector | |
| texCUBElod(s,t) | 使用LOD查找纹理s在t.w位置的color4 | |
| texCUBEbias(s,t) | 将t.w决定的某个MIP层偏置后的一维纹理查找 | |
| texCUBEgrad(s,t,ddx,ddy) | 使用微分并制定MIP层的一维纹理查找 | |
| texCUBEproj(s,t) | 把纹理当做一张幻灯片投影到场景中,先试用投影纹理技术需要计算出投影纹理坐标t(坐标t.w除以透视值),然后使用投影纹理坐标进行查询 |
参考链接:
Cg(C for Graphic)语言标准函数库之纹理映射函数,偏导函数,与调试函数_liu_lin_xm的博客-CSDN博客
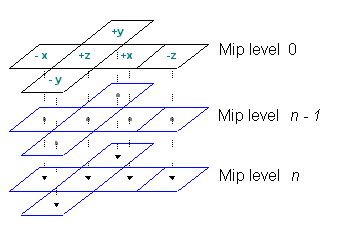
Mipmap:
MipMap的LOD实现原理_tex2dgrad_jieniyimiao的博客-CSDN博客
Unity中关于 Mipmap_mipmaps_u010019717的博客-CSDN博客
2D:
tex2Dbias
3D:
Introduction To Textures in Direct3D 11 - Win32 apps | Microsoft Learn
Texture Coordinates (Direct3D 9) - Win32 apps | Microsoft Learn
3D Textures
立体纹理查找:
Cubic Environment Mapping (Direct3D 9) - Win32 apps | Microsoft Learn
作业:
写出你觉得最常用的5个函数
- tex2D(s,t)
- normalize(x)
- saturate(x)
- dot(x,y)
- lerp(x,y,t)
ddx、ddy的实际使用测试
1.锐化图像
fixed4 frag (v2f i) : SV_Target{fixed4 col = tex2D(_MainTex, i.uv);col += ddx(col * _DDXIntensity)+ ddy(col * _DDYIntensity);return fixed4(col.rgb,1.0);}右图为锐化intensity=1时

最后输出ddx(col * _DDXIntensity)+ ddy(col * _DDYIntensity)则可以看到锐化范围。

2.求面法线
struct appdata
{float4 vertex : POSITION;float2 uv : TEXCOORD0;float3 normal : TEXCOORD3;
};struct v2f
{float2 uv : TEXCOORD0;UNITY_FOG_COORDS(1)float4 vertex : SV_POSITION;float3 pos : TEXCOORD1;float3 worldPos : TEXCOORD2;float3 worldNormal : TEXCOORD3;
};sampler2D _MainTex;
float4 _MainTex_ST;
float _Intensity;
float _DDXIntensity;
float _DDYIntensity;v2f vert (appdata v)
{v2f o;o.uv = TRANSFORM_TEX(v.uv, _MainTex);o.vertex = UnityObjectToClipPos(v.vertex);o.worldPos = mul(unity_ObjectToWorld,v.vertex).xyz;o.worldNormal = mul(v.vertex,(float3x3)unity_WorldToObject).xyz;return o;
}fixed4 frag (v2f i) : SV_Target
{fixed3 col = tex2D(_MainTex, i.uv);//锐化//col += ddx(col * _DDXIntensity)+ ddy(col * _DDYIntensity);//求面法线col = normalize(cross(ddy(i.worldPos),ddx(i.worldPos))); return fixed4(col,1.0);
}
相关文章:

2.3 HLSL常用函数
一、函数介绍 函数图像参考网站:Graphtoy 1.基本数学运算 函数 含义 示例图 min(a,b) 返回a、b中较小的数值 mul(a,b) 两数相乘用于矩阵计算 max(a,b) 返回a、b中较大的数值 abs(a) 返回a的绝对值 round(x) 返回与x最近的整数 sqrt(x) 返回x的…...

互联网的发展
概述 互联网是现代社会中举足轻重的一个领域,它的发展对于人类的生活和工作方式产生了深远的影响。互联网的发展经历了几个阶段,从初创阶段到如今的高度普及和深入应用,本文将详细介绍互联网的发展状况。 第一阶段:互联网的起源…...
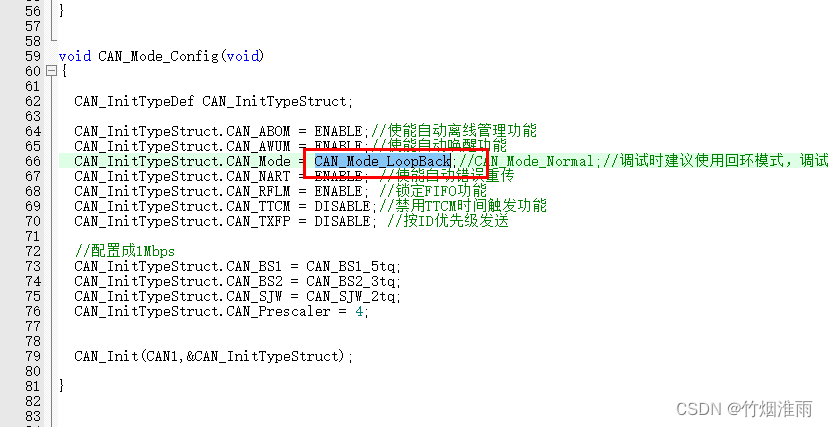
STM32 CAN通讯实验程序
目录 STM32 CAN通讯实验 CAN硬件原理图 CAN外设原理图 TJA1050T硬件描述 实验线路图 回环实验 CAN头文件配置 CAN_GPIO_Config初始化 CAN初始化结构体 CAN筛选器结构体 接收中断优先级配置 接收中断函数 main文件 实验现象 补充 STM32 CAN通讯实验 CAN硬件原理图…...

Python代码片段之Django静态文件URL的配置
首先要说明这段python代码并不完整,而且我也没有做过测试,只是我在工作时参考了其中的一些个方法。这是我在找python相关源码资料里看到的一段代码,是Django静态文件URL配置代码片段2,代码中有些方法还是挺技巧的,做其…...

基于飞桨paddle的极简方案构建手写数字识别模型测试代码
基于飞桨paddle的极简方案构建手写数字识别模型测试代码 原始测试图片为255X252的图片 因为是极简方案采用的是线性回归模型,所以预测结果数字不一致 本次预测的数字是 [[3]] 测试结果: PS E:\project\python> & D:/Python39/python.exe e:/pro…...

soft ip与hard ip
ip分soft和hard两种,soft就是纯代码,买过来要自己综合自己pr。hard ip如mem和analog与工艺有关。 mem的lib和lef是memory compiler产生的,基于bitcell,是foundry给的。 我正在「拾陆楼」和朋友们讨论有趣的话题,你⼀起…...
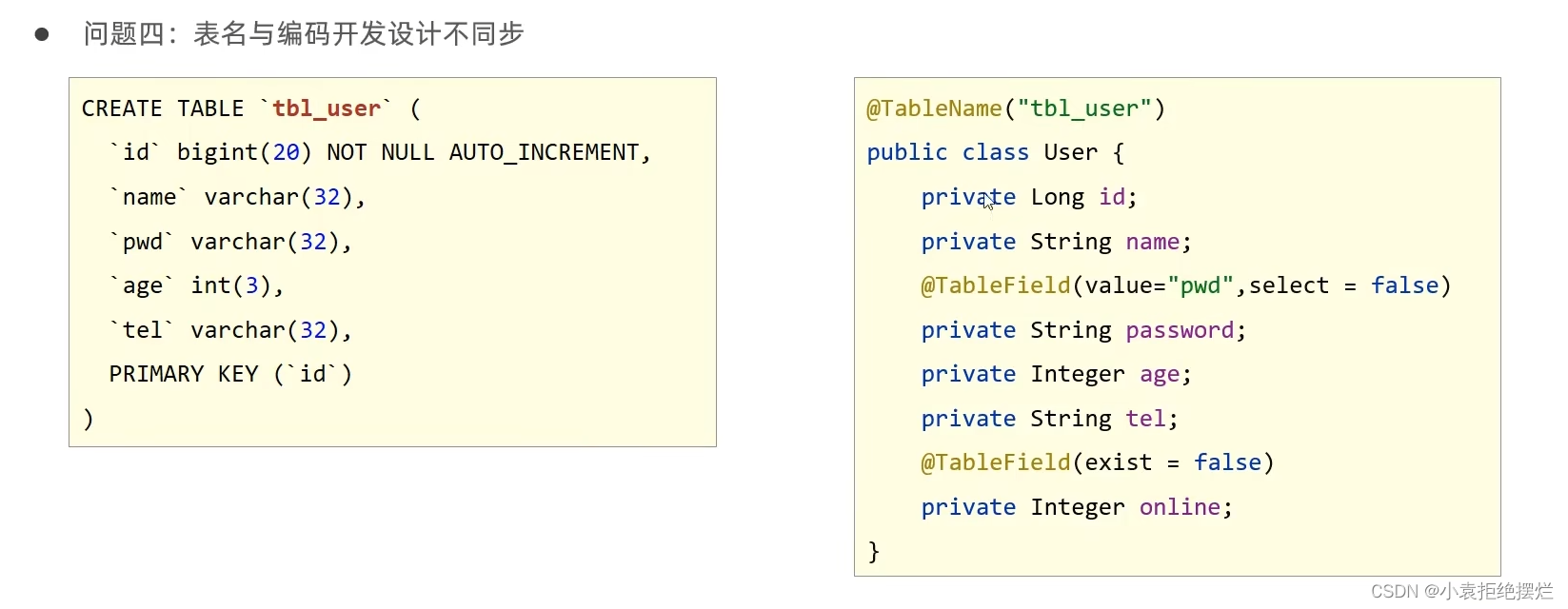
MyBatisPlus从入门到精通-2
接着上一讲的Mp的分页功能 下面我们讲解条件查询功能和其他功能 解决一下日志输出和banner问题 每次卞就会输出这些日志 很不美观,现在我们关闭一下 这样建个xml,文件名为logback.xml 文件内容改成这样 配置了logback但是里面什么都没写就不会说有日…...
)
AI面试官:Asp.Net 中使用Log4Net (一)
AI面试官:Asp.Net 中使用Log4Net (一) 当面试涉及到使用log4net日志记录框架的相关问题时,通常会聚焦在如何在.NET或.NET Core应用程序中集成和使用log4net。以下是一些关于log4net的面试题目,以及相应的解答、案例和代码: 文章目…...

Selenium自动化元素定位方式与浏览器测试脚本
Selenium八大元素定位方法 Selenium可以驱动浏览器完成各种操作,比如模拟点击等。要想操作一个元素,首先应该识别这个元素。人有各种的特征(属性),我们可以通过其特征找到人,如通过身份证号、姓名、家庭住…...

人机交互与人机混合智能的区别
人机交互和人机融合智能是两个相关但不完全相同的概念: 人机交互是指人与计算机之间的信息交流和互动过程。它关注的是如何设计和实现用户友好的界面,以便人们能够方便、高效地与计算机进行沟通和操作。人机交互通常强调用户体验和界面设计,旨…...

【项目】轻量级HTTP服务器
文章目录 一、项目介绍二、前置知识2.1 URI、URL、URN2.2 CGI2.2.1 CGI的概念2.2.2 CGI模式的实现2.2.3 CGI的意义 三、项目设计3.1 日志的编写3.2 套接字编写3.3 HTTP服务器实现3.4 HTTP请求与响应结构3.5 EndPoint类的实现3.5.1 EndPoint的基本逻辑3.5.2 读取请求3.5.3 构建响…...

sketch如何在线打开?有没有什么软件可以辅助
Sketch 在线打开的方法有哪些?这个问题和我之前回答过的「Sketch 可以在线编辑吗?」是一样的答案,没有。很遗憾,Sketch 没有在线打开的方法,Sketch 也做不到可以在线编辑。那么,那些广告里出现的设计软件工…...

CSS Flex 笔记
1. Flexbox 术语 Flex 容器可以是<div> 等,对其设置属性:display: flex, justify-content 是沿主轴方向调整元素,align-items 是沿交叉轴对齐元素。 2. Cheatsheet 2.1 设置 Flex 容器,加粗的属性为默认值 2.1.1 align-it…...

Markdown常用标签及其用途-有示例
Markdown常用标签及其用途 Markdown是一种轻量级标记语言,具有简洁易读的特点。下面是一些常用的Markdown标签以及它们的用途,并附带一些示例: 标题 用于创建不同级别的标题,可通过添加一到六个#符号来表示不同级别的标题。 #…...
25.1 Knife4j-Swagger的增强插件
1.Knife4j概述 Knife4j是一款基于Swagger UI的增强插件,它可以为Spring Boot项目生成美观且易于使用的API文档界面。它是Swagger UI的增强版,提供了更多的功能和定制选项,使API文档更加易读和易于理解。 2.Knife4j使用 Knife4j 集Swagger2…...

用flask run代替flask run --debug
安装python-dotenv依赖。 在项目根目录下新建.flaskenv文件,并作如下配置: FLASK_ENVdevelopment FLASK_DEBUG1...
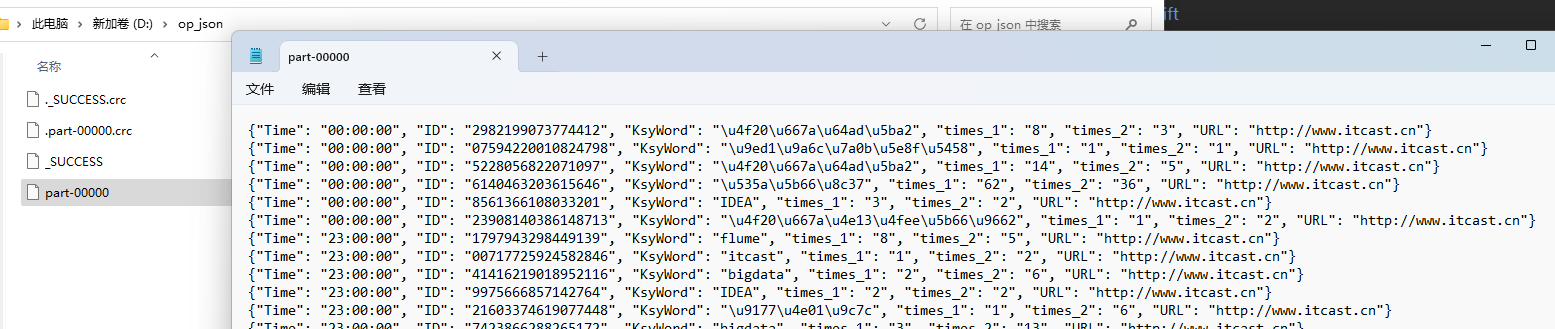
python_day14_综合案例
文件内容 导包配置 import jsonfrom pyspark import SparkContext, SparkConf import osos.environ["PYSPARK_PYTHON"] "D:/dev/python/python3.10.4/python.exe" os.environ["HADOOP_HOME"] "D:/dev/hadoop-3.0.0" conf SparkC…...

【算法题】2779. 数组的最大美丽值
题目: 给你一个下标从 0 开始的整数数组 nums 和一个 非负 整数 k 。 在一步操作中,你可以执行下述指令: 在范围 [0, nums.length - 1] 中选择一个 此前没有选过 的下标 i 。 将 nums[i] 替换为范围 [nums[i] - k, nums[i] k] 内的任一整…...

文件上传之PHP
别怕,我会一直陪着你 一.知识二.实例1.phtml, <?简单过滤2.前端验证, phtml3 \.htaccess 一.知识 绕过后缀的有文件格式有php,php3,php4,php5,phtml.pht 二.实例 1.phtml, <?简单过滤 (1)一句话木马 故意使用了post和get用来迷惑人 https://127.0.0.1/shy.php?POS…...

人脸检测实战-insightface
目录 简介 一、InsightFace介绍 二、安装 三、快速体验 四、代码实战 1、人脸检测 2、人脸识别 五、代码及示例图片链接 简介 目前github有非常多的人脸识别开源项目,下面列出几个常用的开源项目: 1、deepface 2、CompreFace 3、face_recogn…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...