数据结构<堆>
🎇🎇🎇作者:
@小鱼不会骑车
🎆🎆🎆专栏:
《数据结构》
🎓🎓🎓个人简介:
一名专科大一在读的小比特,努力学习编程是我唯一的出路😎😎😎
优先级队列(堆)
- 1. 优先级队列
- 1.1 概念
- 2. 优先级队列的模拟实现
- 2.1 堆的概念
- 2.2 堆的存储方式
- 2.3 堆的创建
- 2.3.1 堆向下调整
- 2.3.2 建堆的时间复杂度
- 2.3.3 堆的向上调整
- 插入举例:
- 建堆举例:
- 2.3.4 堆的删除
1. 优先级队列
1.1 概念
小鱼在之前的一篇博客中详细的介绍过队列,队列是一种先进先出(FIFO)的数据结构,但是有些情况下,操作的数据可能带有优先级,一般出队列时,可能需要优先级高的元素先出队列,例如我们在追剧时,如果是电池没电了,手机会优先提醒我们该充电了,而不是在等到你退出追剧的时候才弹出来,这时候就体现了优先级的重要性,包括打游戏时突然来电话,万一是很重要的电话,没有第一时间接到,是不是就可能产生很严重的后果!
在这种情况下,数据结构应该提高两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象.这种数据结构就是优先级队列(Priority Queue).
2. 优先级队列的模拟实现
JDK1.8中的PriorityQueue底层使用了堆这种数据结构,而堆实际就是在完全二叉树的基础上进行了一些调整.
2.1 堆的概念
如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中,并满足:Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0,1,2…,则称为 小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
堆的性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值;
- 堆总是一棵完全二叉树。
如下图:
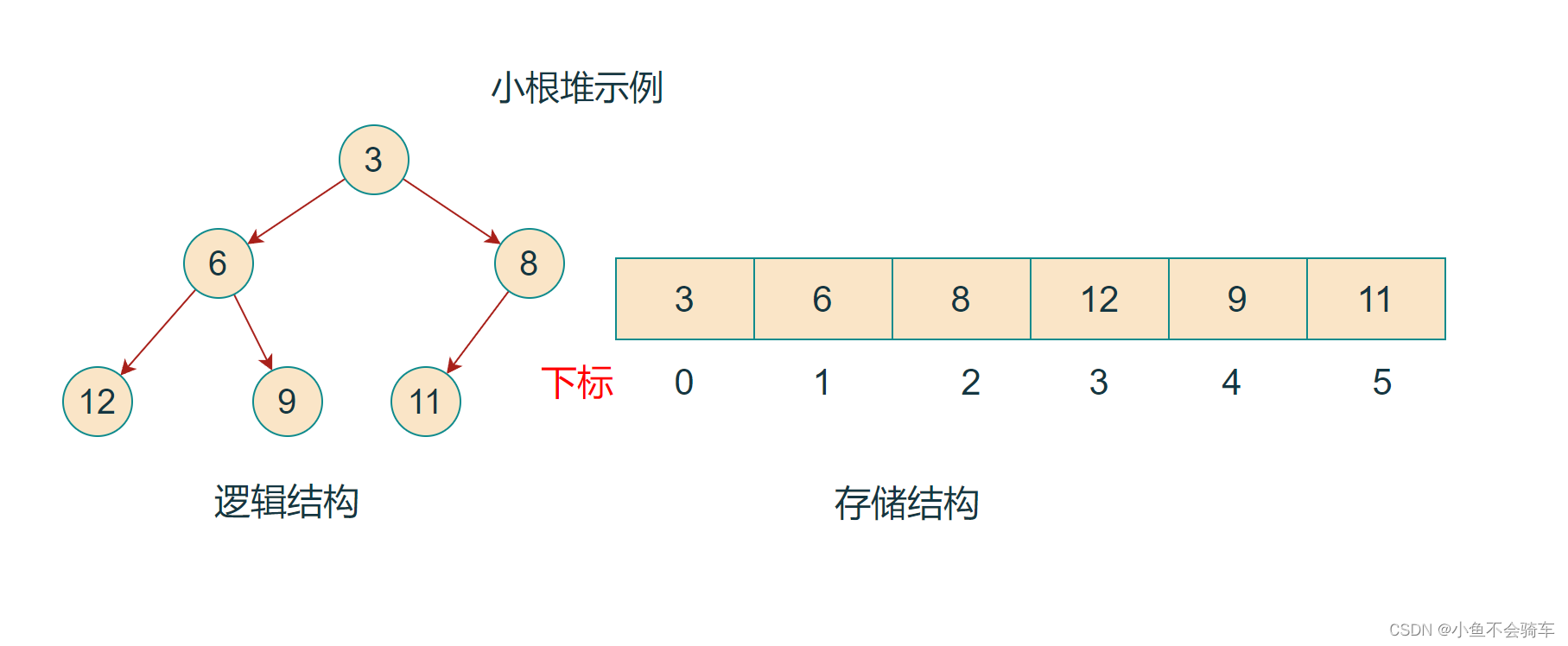
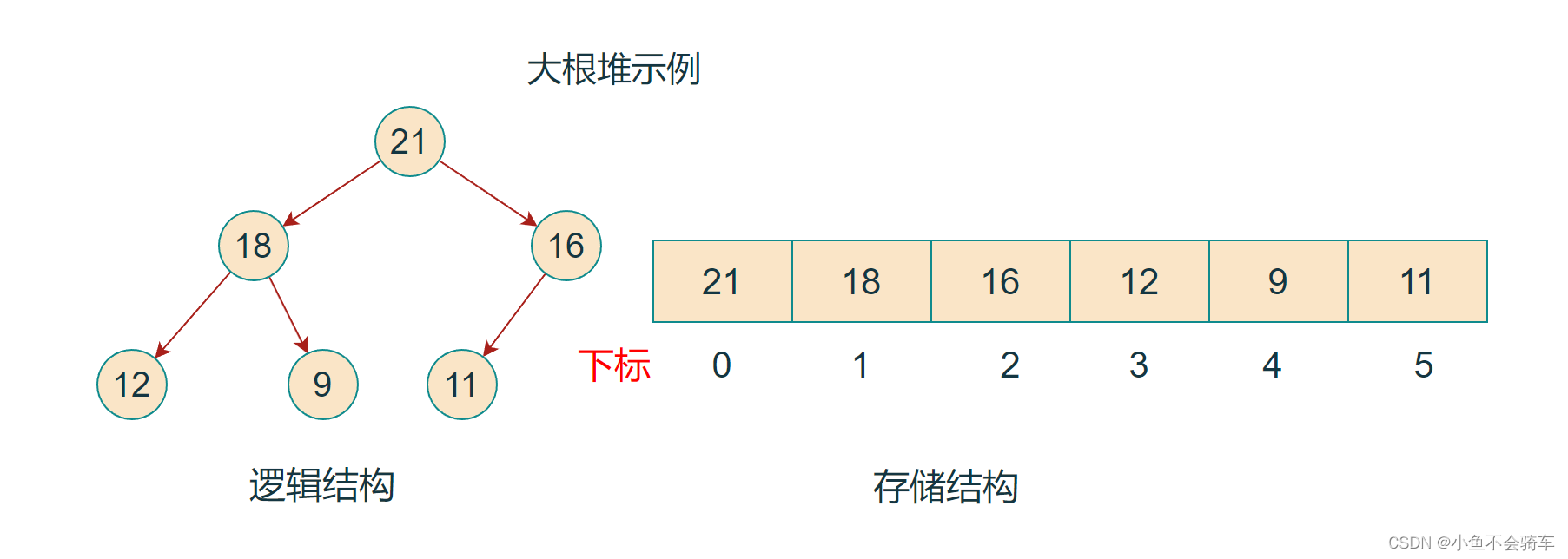
2.2 堆的存储方式
从堆的概念可知,堆是一颗完全二叉树,因此可以按照层序遍历的规则采用顺序的方式来高效存储.
对于非完全二叉树实现的堆,如下图,该二叉树会造成空间上的浪费.

因此:对于非完全二叉树,则不适合使用顺序方式进行存储,因为为了能够还原二叉树,空间中必须要存储空节点,就会导致空间利用率比较低。
完全二叉树实现的堆如下图:

2.3 堆的创建
2.3.1 堆向下调整
对于集合{ 23,25,64,35,18,29,33,14,16,27 }中的数据,如果将其创建成堆呢?
我们先把它的逻辑结构画出来!
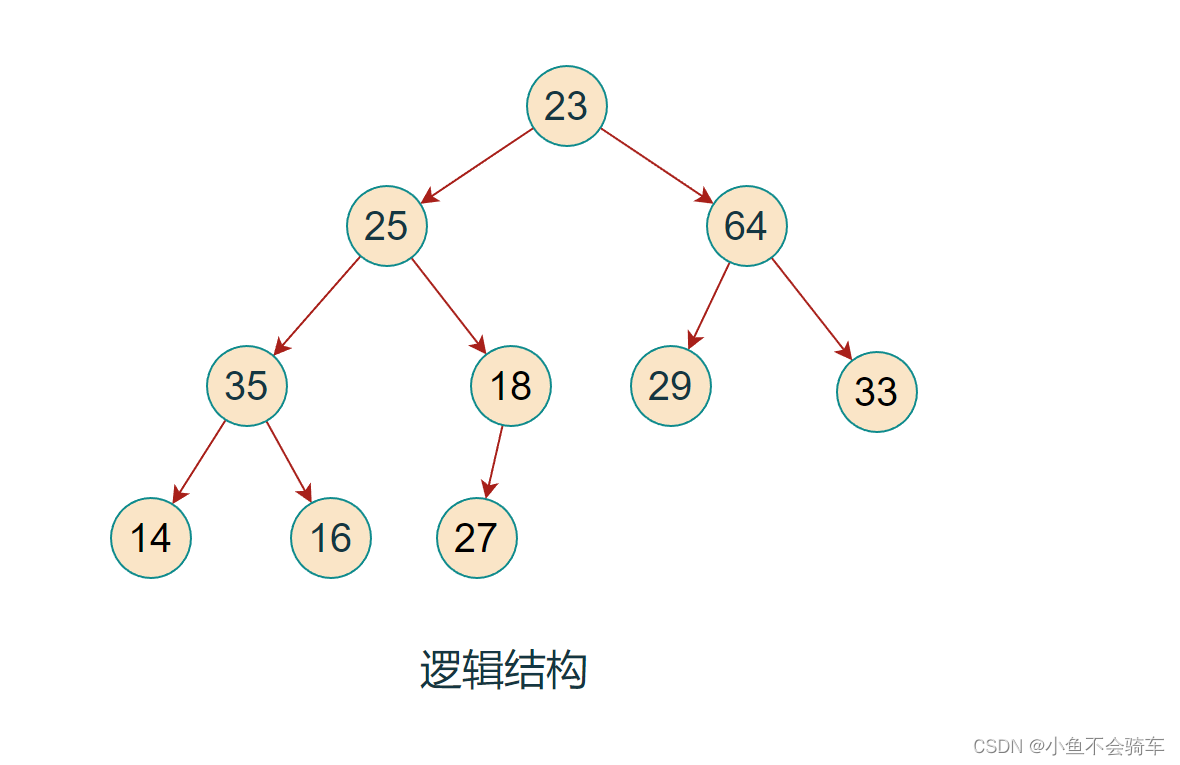
我们需要将该结构调整为大根堆.
大家先看过程,一边观看过程,一边理解思路.
步骤一: 找到最后一颗含有孩子节点的树
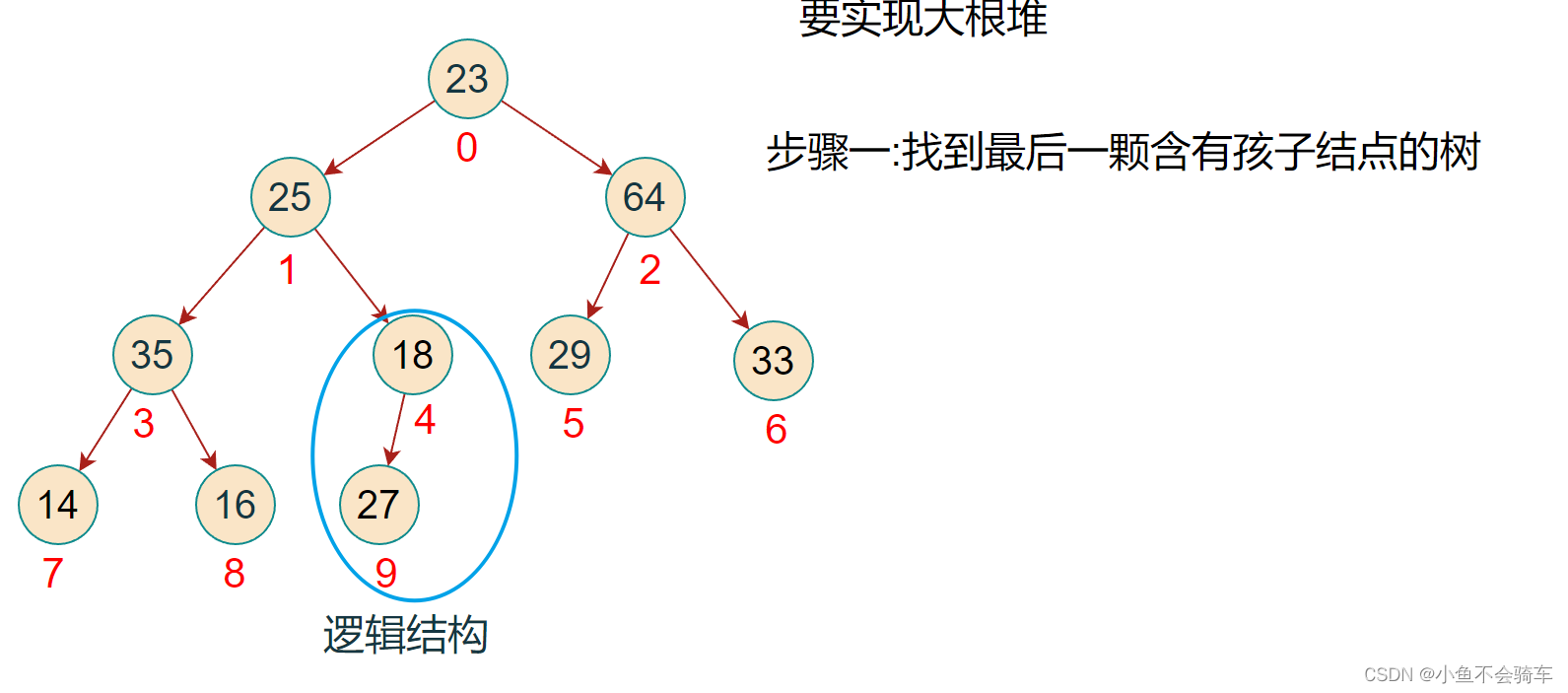
步骤二:
- 判断左右孩子结点是否存在
- 找出左右孩子节点的最大值(大根堆)
- 比较该子树的根节点也就是下标4对应的结点,判断下标为九的结点是否大于根节点
- 如果大于根节点,那就交换,如果小于则不进行交换
步骤三:由于大于子树的根节点,那么进行交换
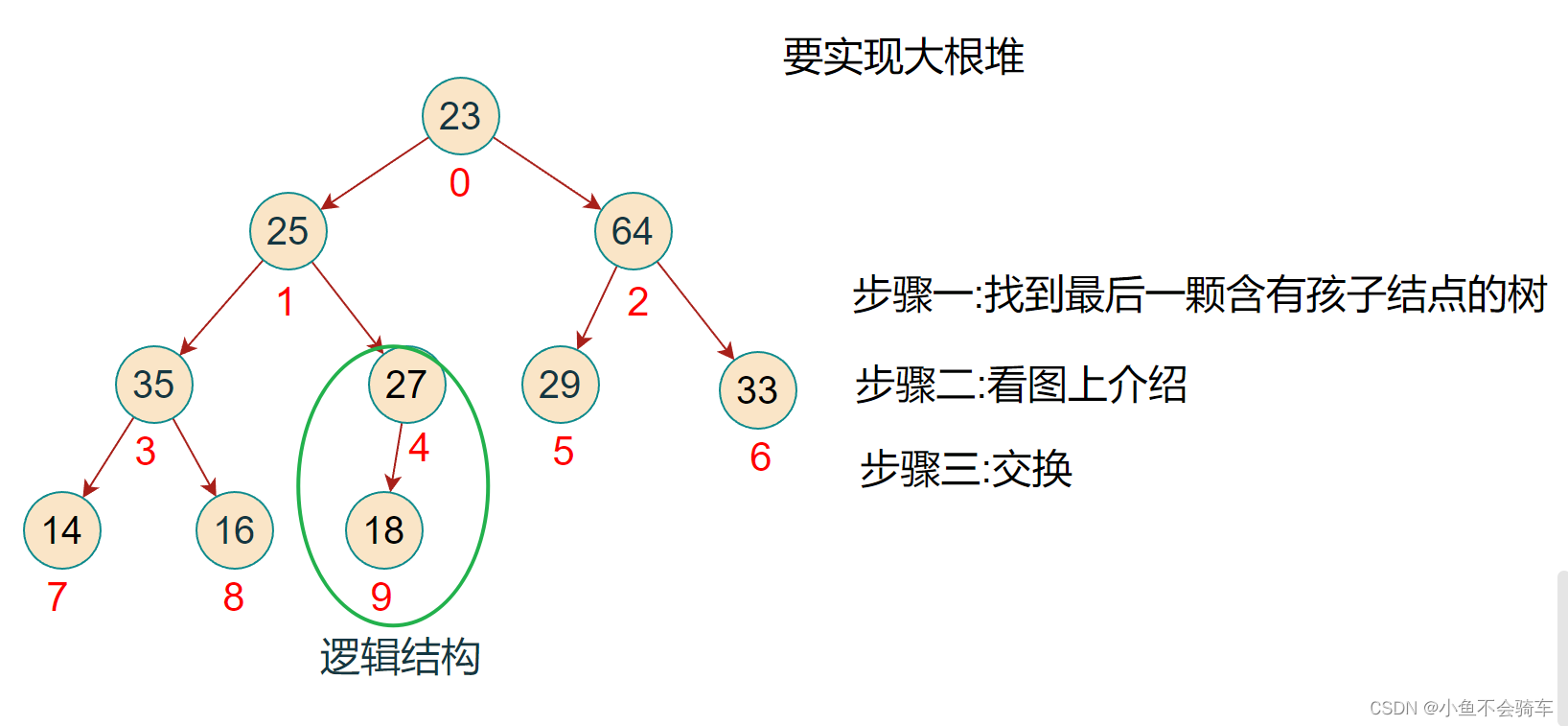
步骤四:下标为4的这个结点对应的子树已经是大根堆了,下一步对下标为3的这个结点,将该树改为大根堆
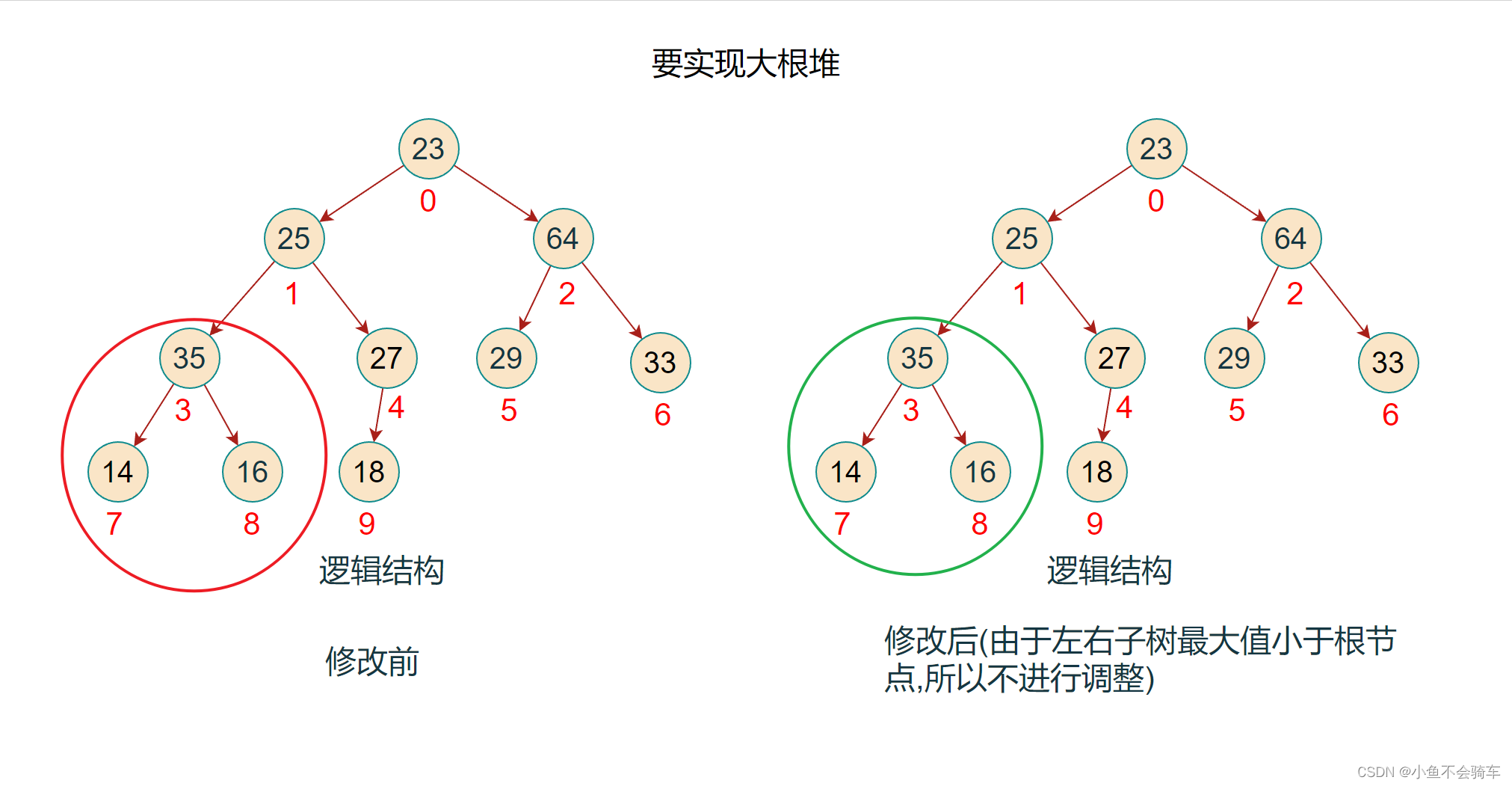
步骤五:重复步骤二,将下标为2的结点对应的子树调整为大根堆
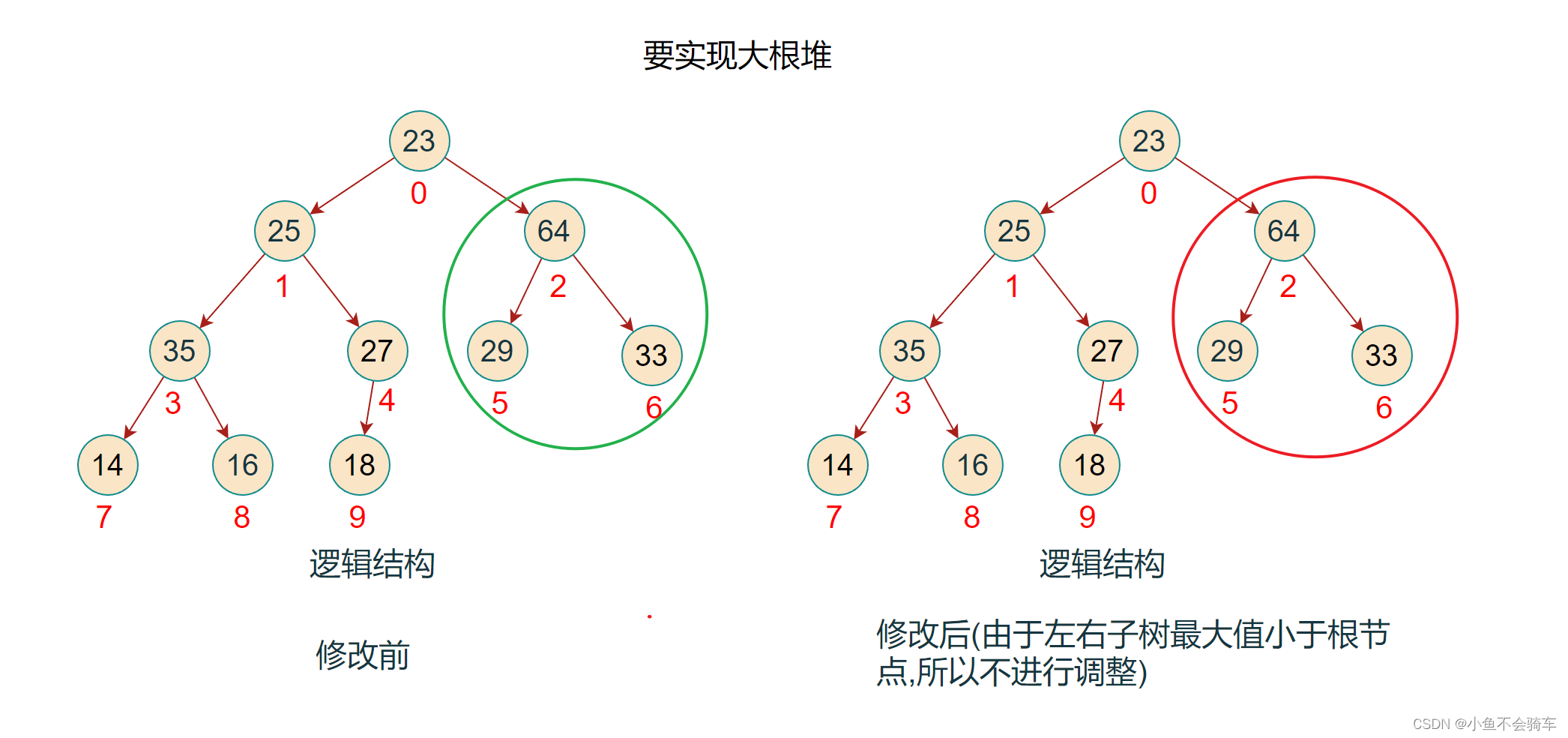
步骤六:对下标为1的结点所对应的树进行调整,依旧是重复上述操作
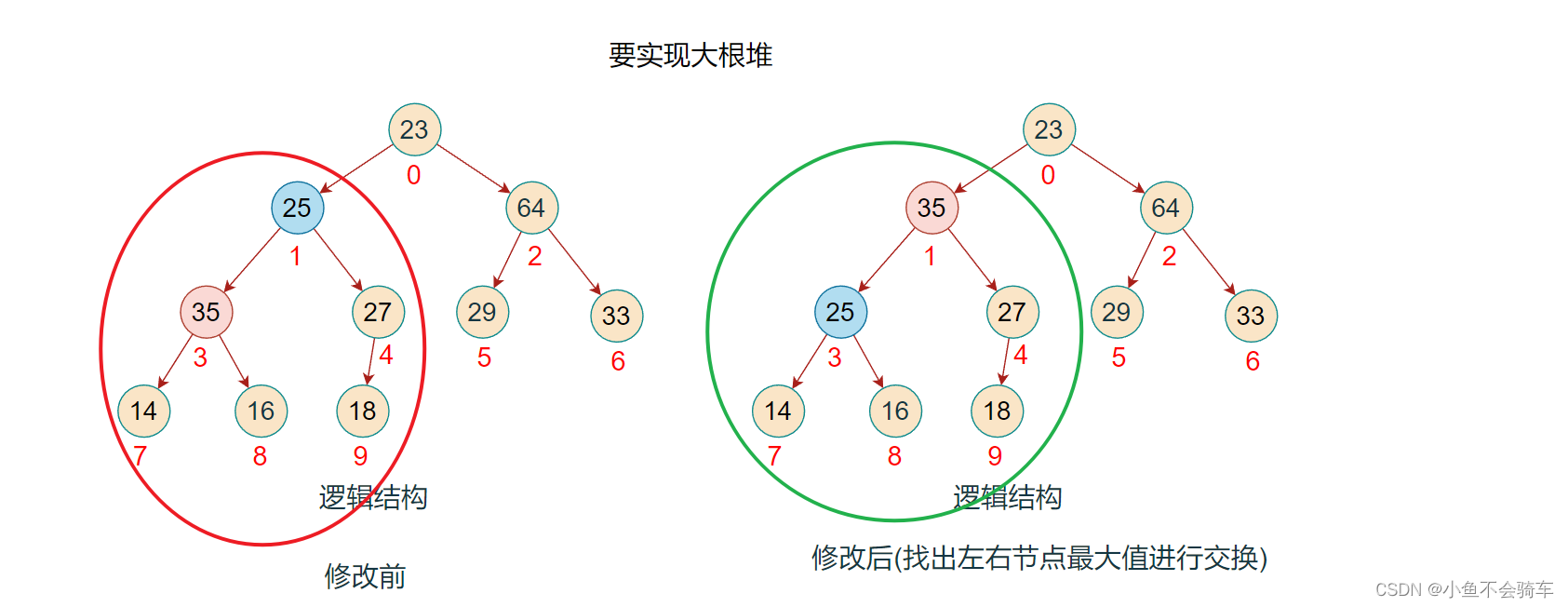
步骤七:此时该子树并没有调整完,需要注意!!!由于下标为1的结点和下标为3的结点进行了交换,那么还需要进行一步操作就是判断,被交换值的下标为3的结点是否是下标为3的节点所对应的这颗树中的最大值!
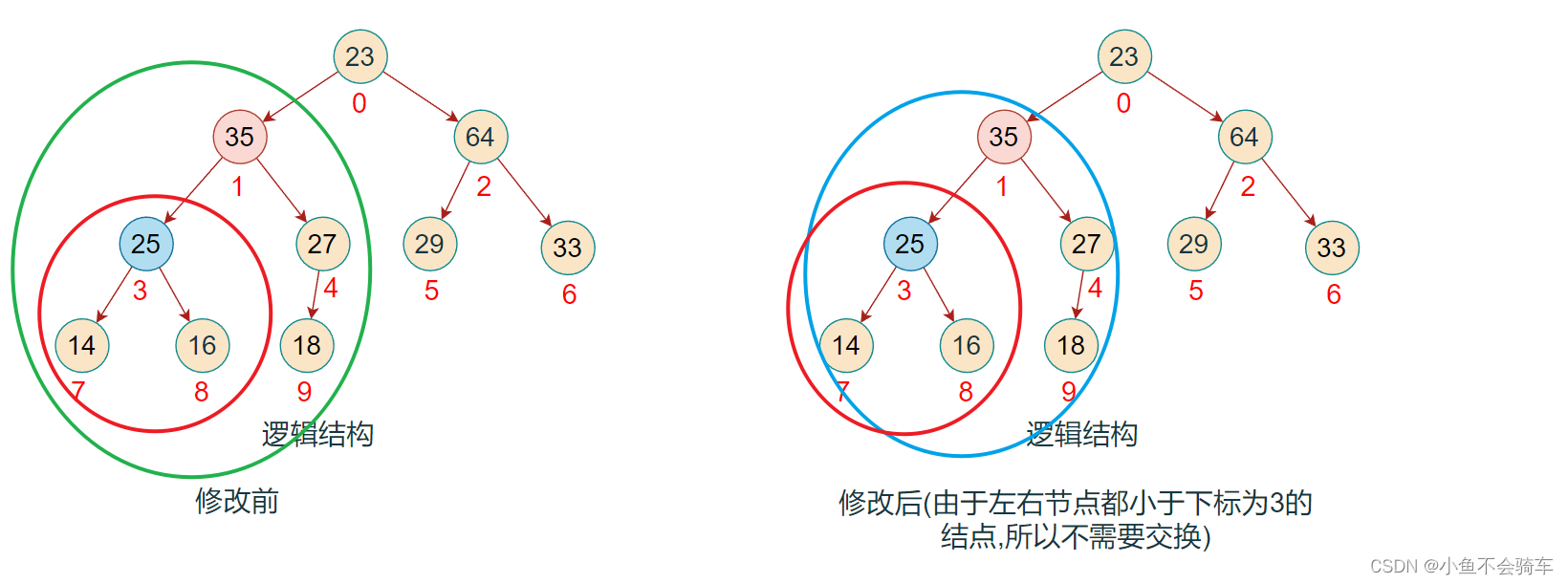
步骤八:现在对下标为0的结点进行调整(下标为2和下标为0的结点进行了交换),红色框对应的是该结点所对应的树,绿色的框是正在进行比较的树
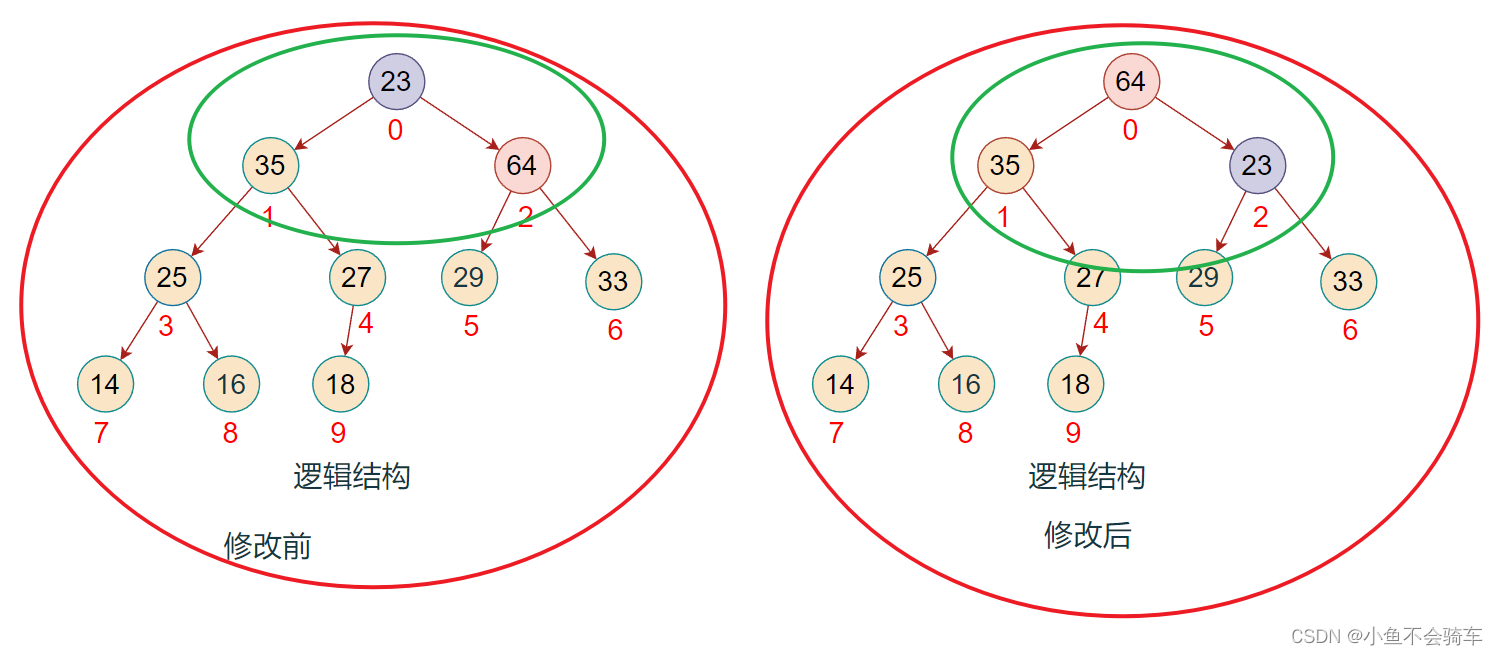
步骤九:由于前面进行了交换,将下标为2的值进行了修改,此时并不能确认下标为2所对应的树是否还是大根堆,所以需要重复步骤二的操作,也就是找出左右孩子结点的最大值进行比较.
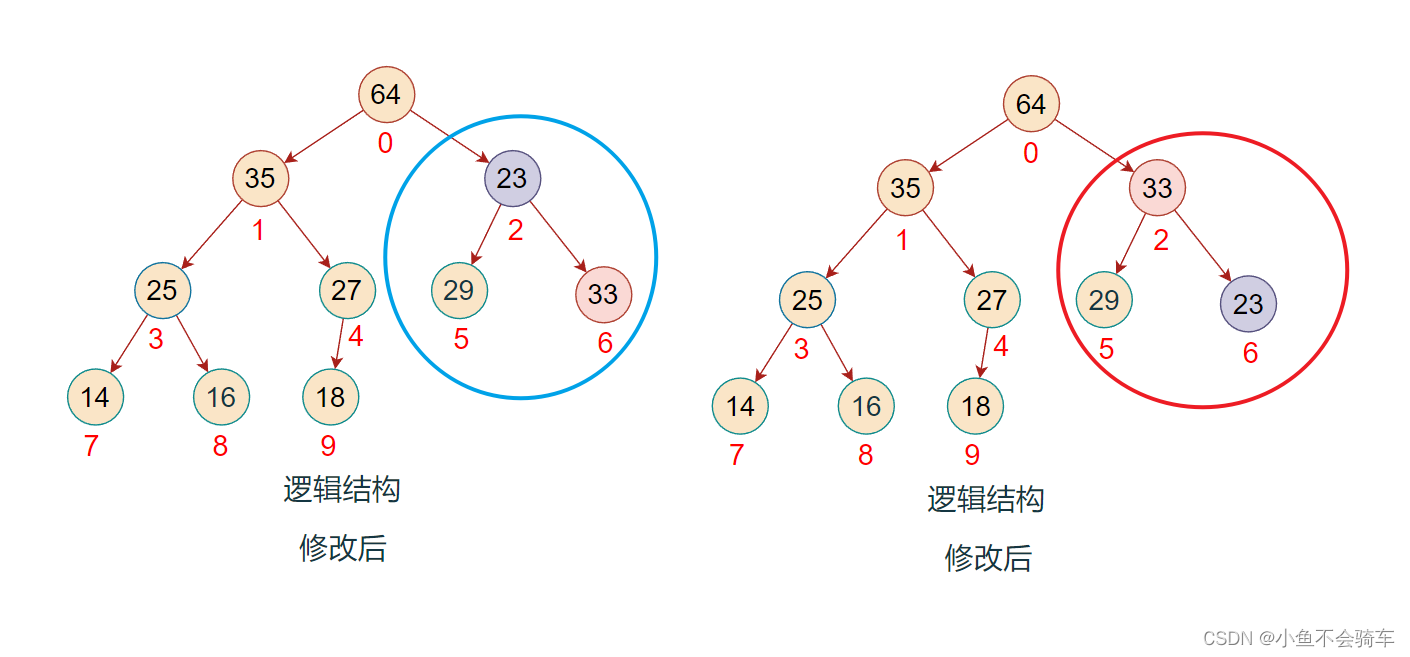
此时,该完全二叉树也就变成了一个大根堆,任何一颗子树的根节点都大于它的任何一个孩子节点.
如下图(每一个框框所对应的树的根节点都大于它的孩子结点):
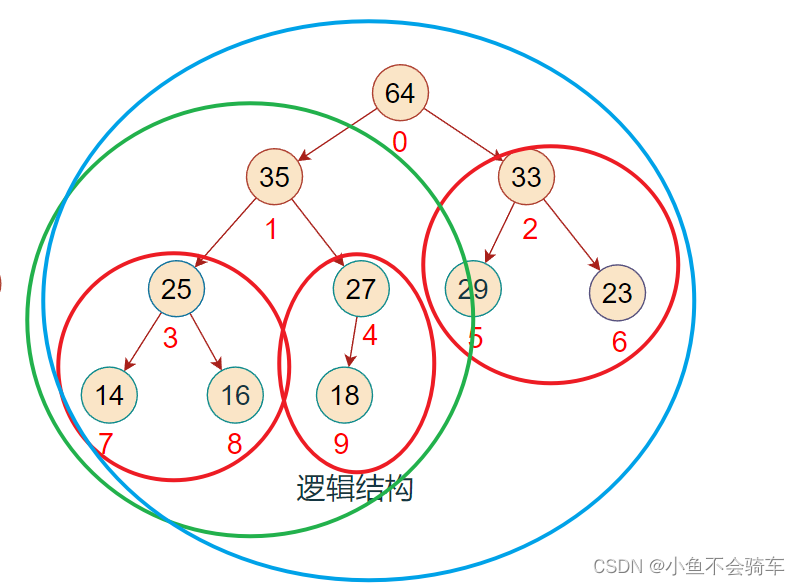
上述的操作我们称之为向下调整.
此时我们再去观看下面的过程是不是更容易理解.
向下过程(以大堆为例):
- 让parent标记需要调整的节点,child标记parent的左孩子(注意:parent如果有孩子一定先是有左孩子)
- 如果parent的左孩子存在,即:child < size, 进行以下操作,直到parent的左孩子不存在:
- parent右孩子是否存在,存在找到左右孩子中最大的孩子,让child指向左右孩子最大值所对应的下标.
- 将parent与较大的孩子child比较,如果:
- parent大于较小的孩子child,调整结束
- 否则:交换parent与较大的孩子child,交换完成之后,parent中小的元素向下移动,可能导致子树不满足对的性质,因此需要继续向下调整,即parent = child;child=parent*2+1; 然后继续2的操作。
难点1:其实对于这道题的难点,就是找向下调整的边界,什么时候停止调整呢?
难点2:为什么要从最后一颗含有子节点的树开始向下调整.
讲解难点一:首先我们要知道,如果想要进行向下调整那么需要最基本的条件就是它有孩子结点,也就是至少存在左孩子,如果左孩子都不存在,那么该节点就不需要进行调整,此时问题就变成了,如何判断左孩子是否存在!
我们看下图:

下标为4的结点是有孩子结点的,孩子结点的下标是9,在二叉树中我们学过,给父亲节点下标,求左右孩子结点的下标,根据公式(求左孩子下标)child = parent * 2 +1.那么它是否有右孩子结点呢?我们看图片可以很清楚的看到他是没有右孩子结点的,我们假设它有右孩子结点,我们求出右孩子结点的下标:4*2+2 = 10,此时右孩子结点的下标为10,但是我们回归该图,该图只有十个结点,又因为下标是从0开始的,那么下标值最高为9,此时右孩子下标是10,说明以及越界了,并不包含右孩子,此时我们就可以找到这个边界,也就是child < 二叉树结点的个数,为了证明该判断的合理性我们试求下标5的孩子节点是否存在,答案是不存在( 5 * 2 + 1 = 11 11 > 二叉树结点的个数,不符合条件),下标6也如此,都是不存在孩子结点的.
讲解难点2:为什么要从最后一个含有子节点的树进行向下调整?
我们先举个反例:
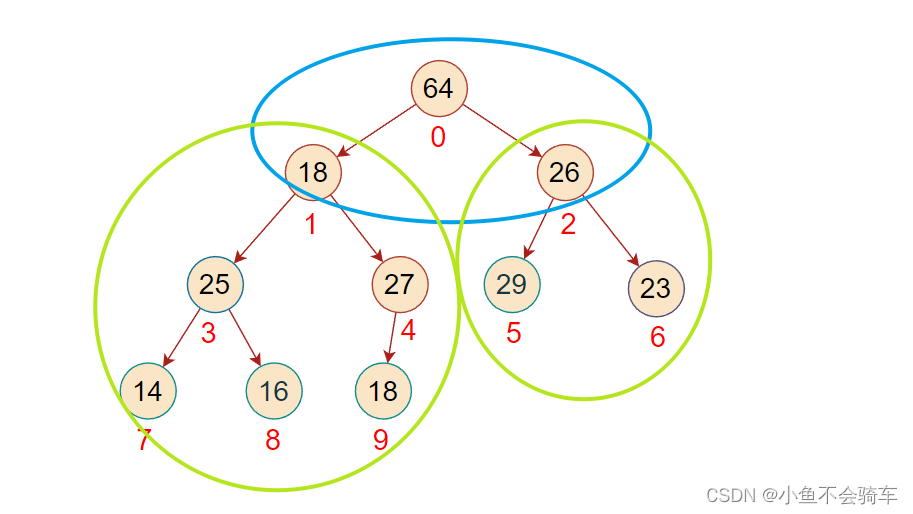
若我们只对0下标对应的结点进行向下调整,大家看上图,此时左右子树都小于根节点,所以不再进行向下调整,但是可以看到,绿色框框里面的树还并不是大根堆,所以从0开始调整是有可能会出错的!
由于我们是从最后一颗子树进行调整的,那么假如我们调整到了下标为1的结点所对应的子树,我们可以保证,比下标1大的下标(例如2,3,4…)所对应的结点的子树一定是大根堆, 而且我们还可以得到一个信息就是:
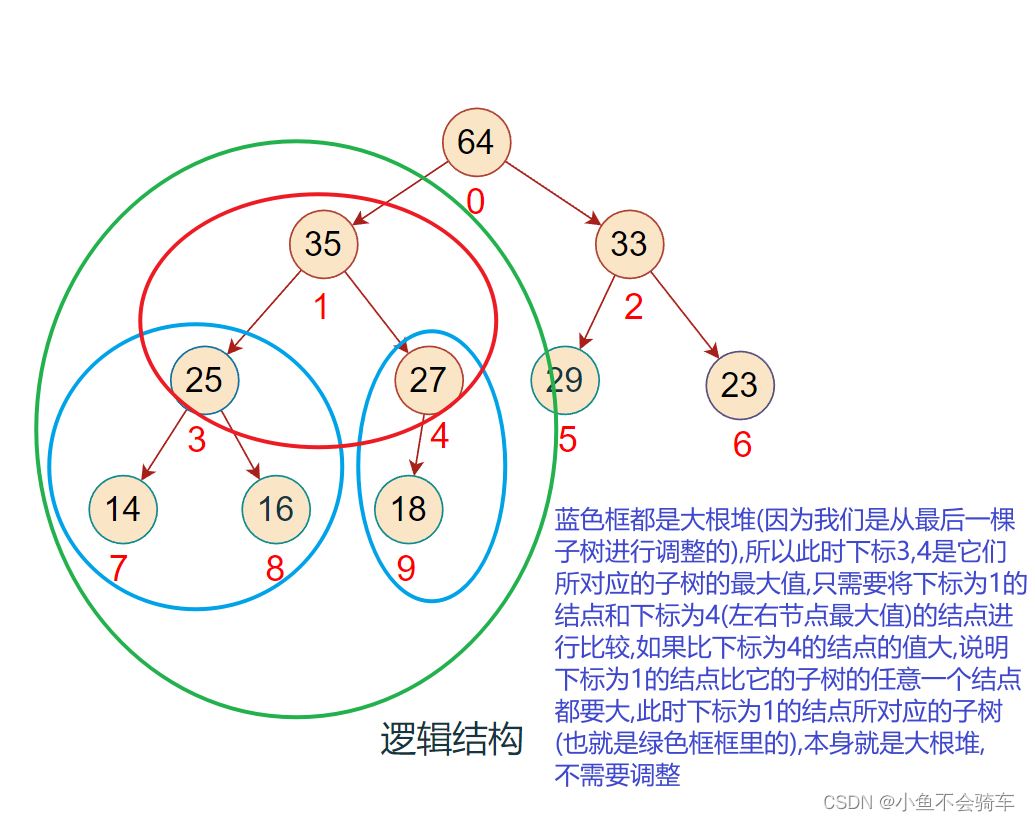
代码如下:
public void createHeap(){//从最后一个结点的父亲结点开始向下调整for (int parent = (UsedSize-1-1)/2; parent >=0 ; parent--) {//UsedSize就是结束条件,也就是节点个数shiftDown(parent,UsedSize);}}/*** 父亲下标和每棵树的结束下标* @param parent*///大根堆private void shiftDown(int parent,int len) {//接受了父亲节点//求出子节点下标int child=2*parent+1;//判断孩子节点下标是否越界while (child<len) {//判断右节点是否存在,如果存在找出左右节点最大值(顺序不能颠倒)if(child+1<len && elem[child]<elem[child+1]) {child++;}//子节点大于父亲节点就交换if(elem[child]>elem[parent]) {swap(elem,parent,child);//此时的父亲节点指向被修改后的子节点parent=child;//子节点依旧是该父亲结点所对应的左孩子结点child=2*parent+1;}else {//如果没有交换就直接退出break;}}}private void swap(int[]array,int left,int right) {int tmp=array[left];array[left]=array[right];array[right]=tmp;}
我们来算一下向下调整的时间复杂度,大家看下图:
时间复杂度分析:
最坏的情况即图示的情况,从根一路比较到叶子,比较的次数为完全二叉树的高度,即时间复杂度为O(logN)
2.3.2 建堆的时间复杂度
我们按照最坏情况考虑,也就是每个结点都需要进行调整,并且每个结点调整的高度都是它所在层数到叶子层数的距离.

则需要移动总的步数为:
T(n) = 2 ^ 0 * ( h - 1 ) + 2 ^ 1*(h - 2) + 2 ^ 2 * ( h - 3) + 2 ^ 3 ( h - 4 ) +…+ 2 ^ ( h - 3 ) * 2 + 2 ^ ( h - 2 ) * 1 ①
2 * T(n) = 2 ^ 1 * ( h - 1 ) + 2 ^ 2(h - 2) + 2 ^ 3 * ( h - 3) + 2 ^ 4 ( h - 4 ) *+…+ 2 ^ ( h - 2 ) * 2 + 2 ^ ( h - 1 ) * 1 ②
② - ① 错位相减:
T(n) = 1 - h + 2 ^ 1 + 2 ^ 2 + 2 ^ 3 + 2 ^ 4 +…+2(h-2)+2^(h-1)
T(n) = 2 ^ 0 + 2 ^ 1 + 2 ^ 2 + 2 ^ 3 + 2 ^ 4 +…+2(h-2)+2^(h-1) - h
T(n) = 2 ^ h - 1 - h
n = 2 ^ h -1
h = log(n+1)
T(n) = n - log(n+1) ≈ n
因此:建堆的时间复杂度为O(N)
2.3.3 堆的向上调整
刚才讲完了向下调整,那么这次我们讲解一下什么是向上调整.
向上调整一般使用的范围是在建堆的时候,还有插入结点的时候.
插入举例:
向上调整需要一个前提,就是当前的堆需要是大根堆(小根堆),我们以大根堆举例:
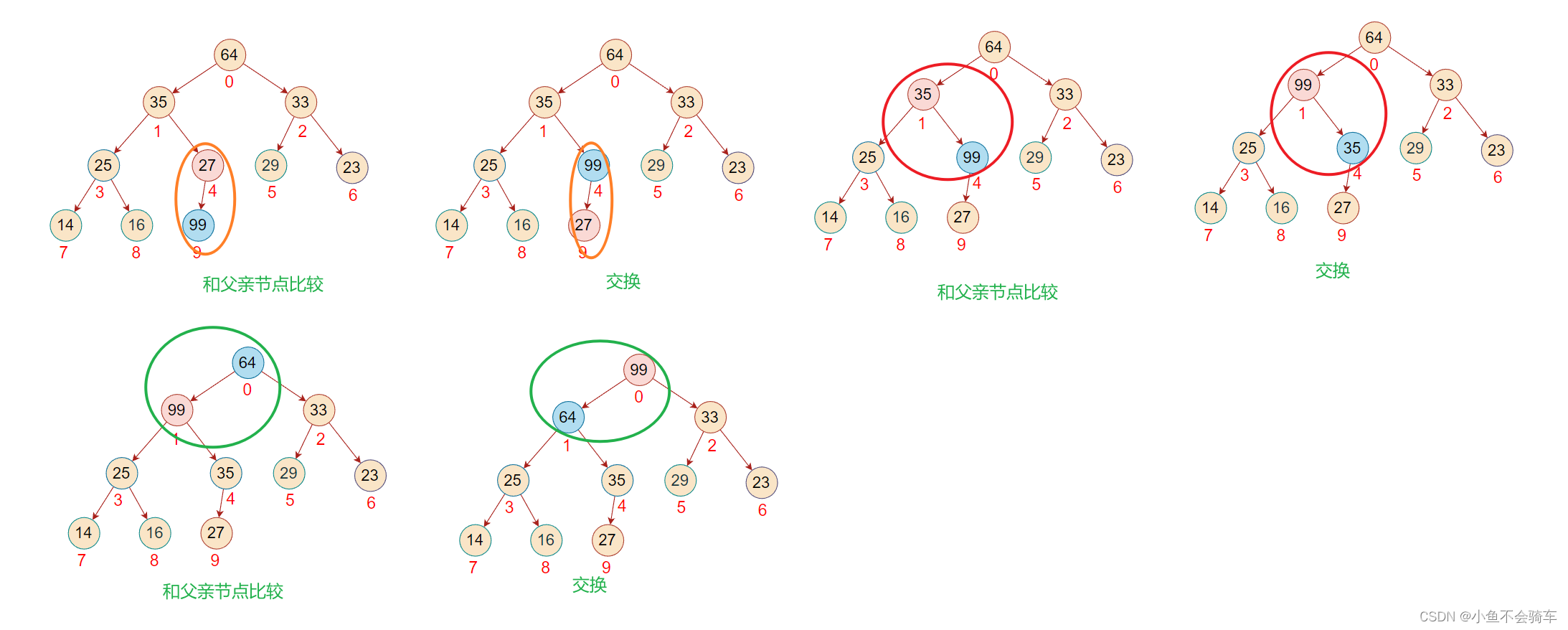
假如99这个结点是新插入的,需要将该树的结构重新改为大根堆,那么需要进行向上调整,具体过程就是:
99和它的父亲节点,也就是下标为4的结点进行比较,如果比父亲节点大,那就交换,此时就跟上述图片的第二步一样,再去用99的结点和它当前的父亲节点进行比较(也就是下标为1的结点),如果比父亲结点大,那就交换,重复上述操作.
问题:不需要左右孩子结点比较吗?
答案:不需要,因为在插入之前,该树就是一个大根堆.
我们用红色框框里面的内容举例:在没有插入99这个结点时,下标为1的结点比下标为3,4结点的值都要大,所以我们可以知道,即使我们的99和下标为4的元素交换,由于下标为3的结点并没有改变,所以我们下标为1的结点还是比下标为3的结点大的,所以就不需要用新的下标为4的结点和下标为3的结点进行比较了.只需要和它的父亲节点进行比较就行.
代码入下:
//插入、public void offer(int val) {//判满if(isFUll()) {elem= Arrays.copyOf(elem,elem.length*2);}//末尾添加新元素然后UsedSize++//UsedSize是记录数组长度的elem[UsedSize++]=val;//进行向上调整,传入最后一个叶子结点shiftUp(UsedSize-1);}//向上调整public void shiftUp(int child) {//找到该结点的父亲结点int parent = (child-1)/2;//边界就是孩子结点不能为0,如果孩子结点为0说明不需要调整了while (child != 0) {//不需要左右孩子结点进行比较,因为该孩子节点的另一个兄弟结点一定小于父亲节点//子节点大于父亲节点就交换if(elem[child] > elem[parent]) {swap(elem,child,parent);}else {//如果不大于那就直接退出break;}//不断地进行向上调整,//可以对照上述画的图片进行理解child = parent;parent = (parent-1)/2;}}
时间复杂度:最坏的情况即图示的情况,从叶子一路比较到根,比较的次数为完全二叉树的高度,即时间复杂度为O(logN)
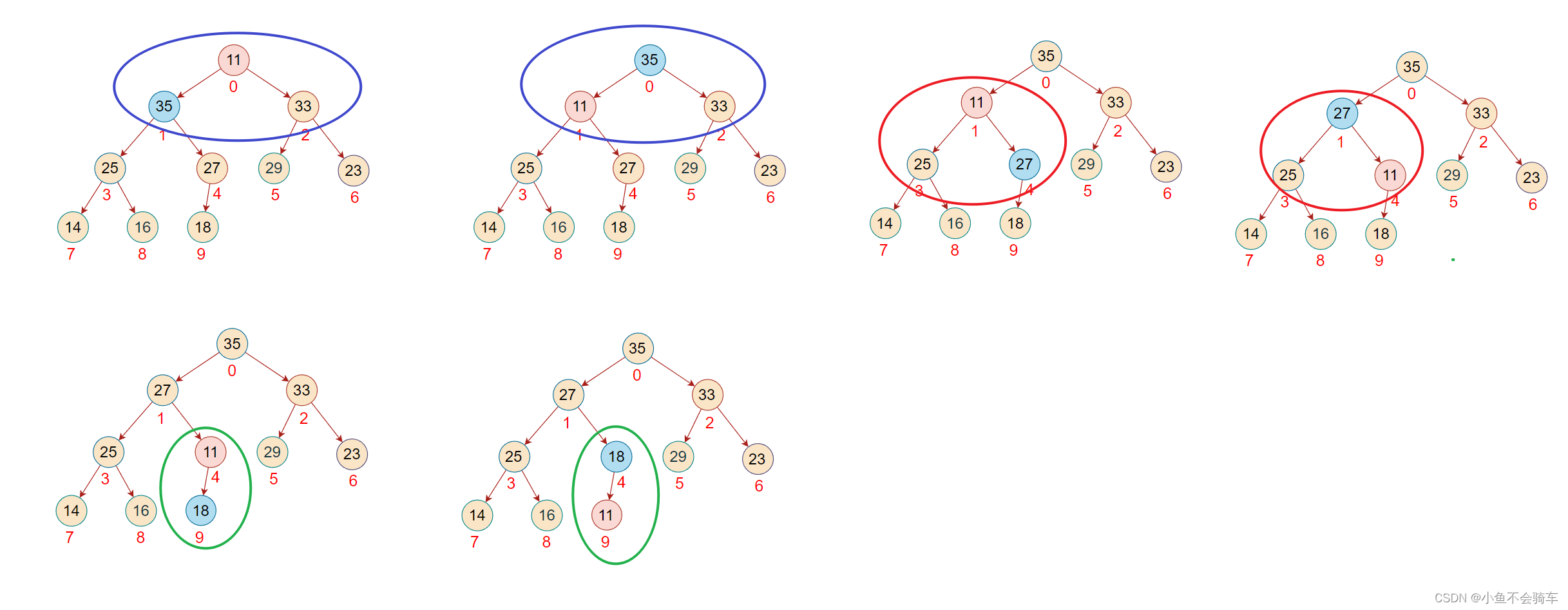
建堆举例:
大家看图:
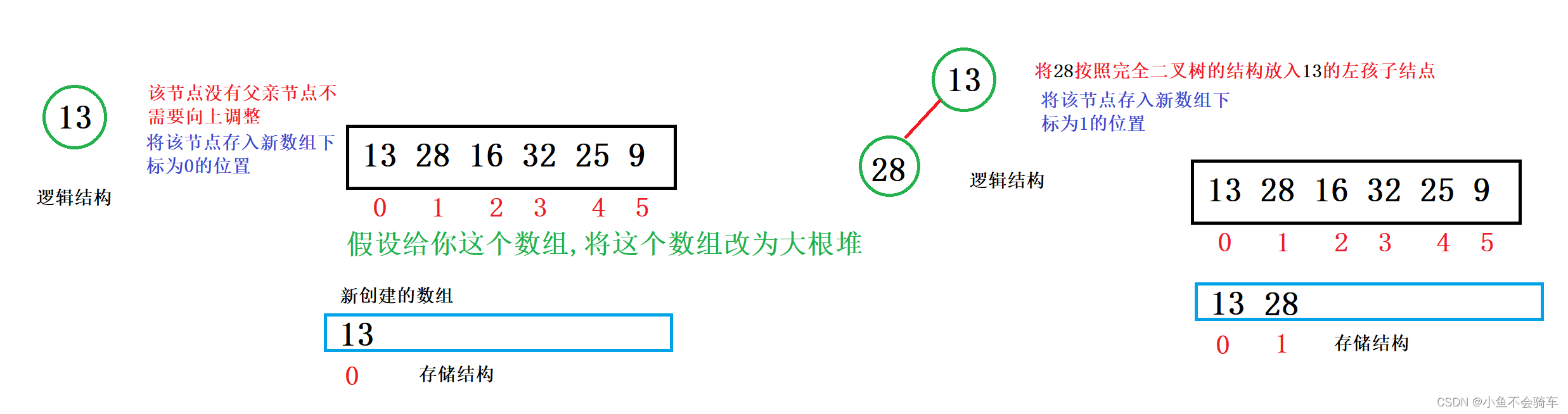
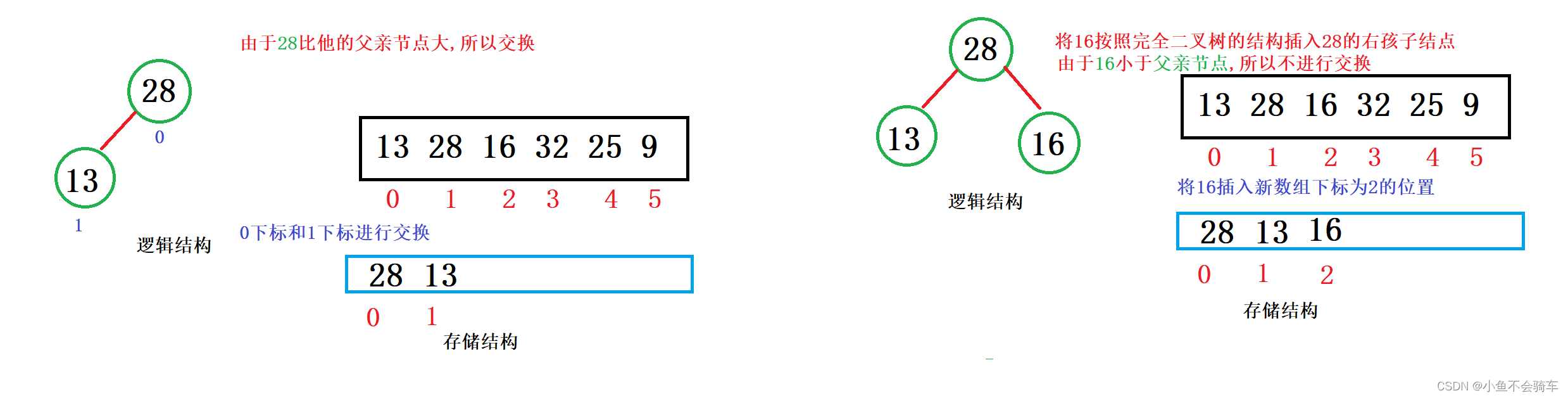
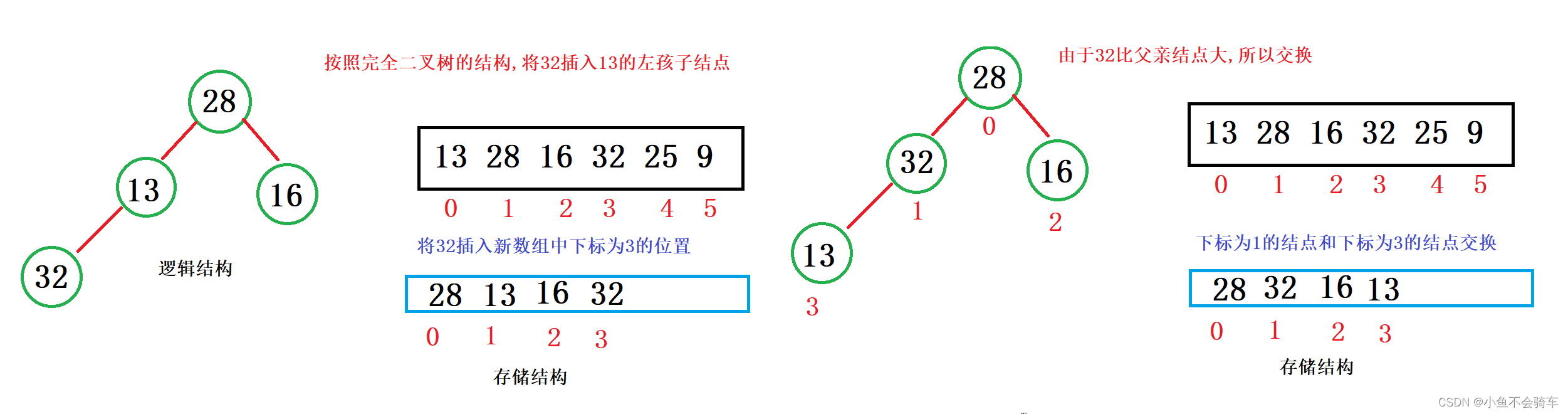
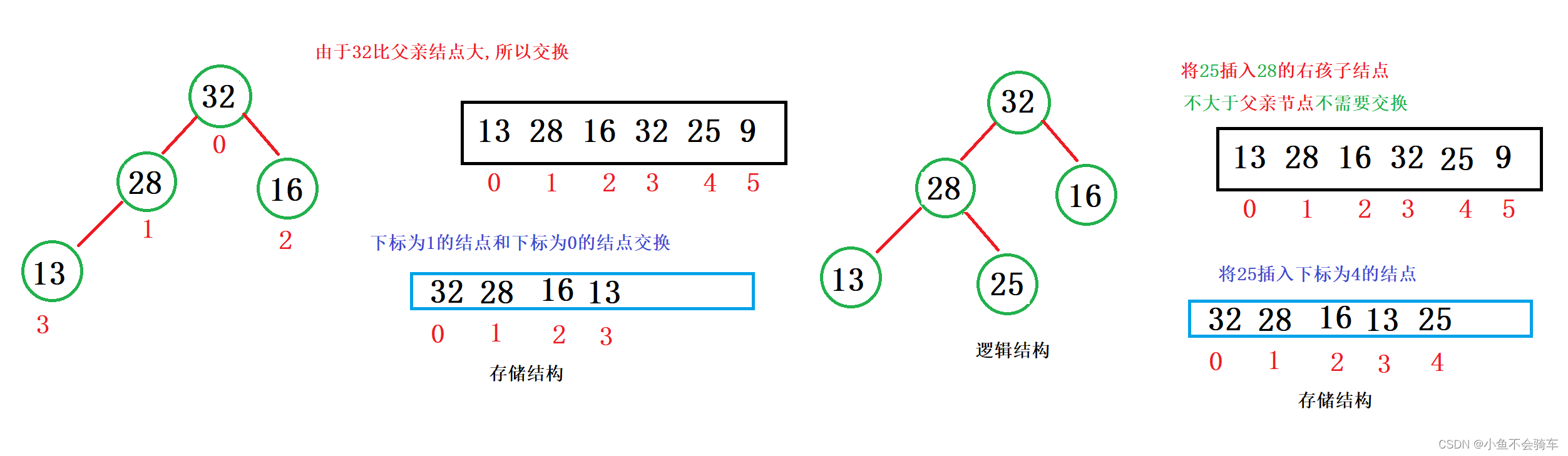

通过上述的过程,我们就通过向上调整建好了一个大根堆.
代码入下:
//建堆public void createHeap(int[] array){for (int i = 0; i < array.length ; i++) {offer(array[i]);}}//插入、public void offer(int val) {//判满if(isFUll()) {elem= Arrays.copyOf(elem,elem.length*2);}//尾插要新增的结点elem[UsedSize++]=val;//将新插入的结点进行向上调整shiftUp(UsedSize-1);}//向上调整public void shiftUp(int child) {int parent = (child-1)/2;while (child != 0) {//子节点大于父亲节点if(elem[child] > elem[parent]) {swap(elem,child,parent);}else {break;}//子节点 = 父节点child = parent;//父节点 = 父节点的父节点parent = (parent-1)/2;}}//交换private void swap(int[]array,int left,int right) {int tmp=array[left];array[left]=array[right];array[right]=tmp;}
2.3.4 堆的删除
由于删除的是堆顶元素,我们思考一下,如何删除?有人会想到:将堆顶元素删除,然后所有元素向前移一位,最后再对每个结点进行向下调整.其实这个方法是行得通的,但却不是一个好的方法,因为所有元素前移一位就会打乱堆本身的顺序,再对堆中的每个元素向下调整,那么时间复杂度最坏可以达到O(N),那有没有什么好一些的方法吗?
答案是:有的.
注意:堆的删除一定删除的是堆顶元素。具体如下:
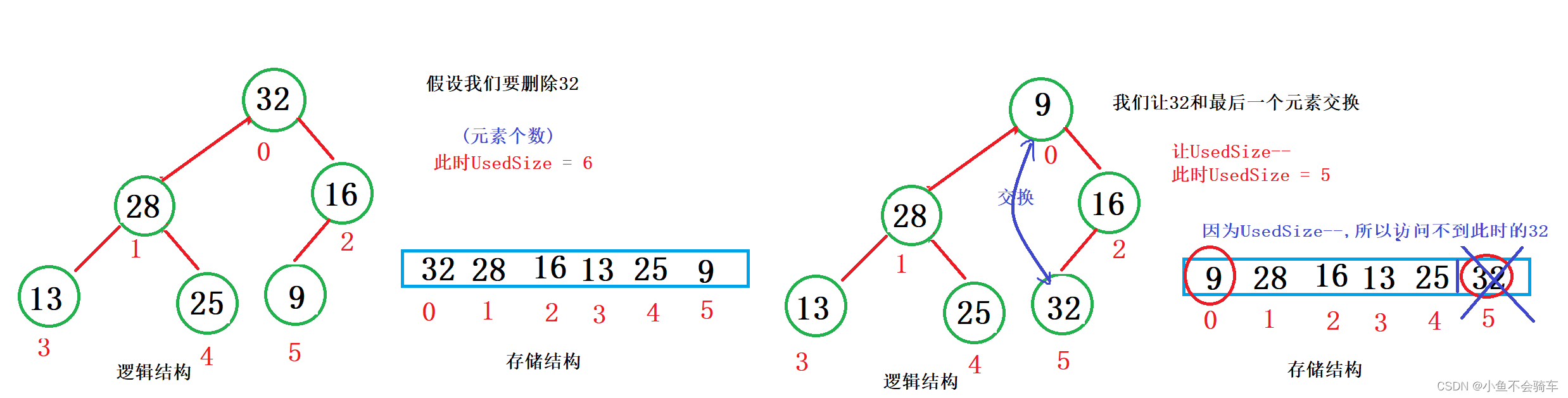
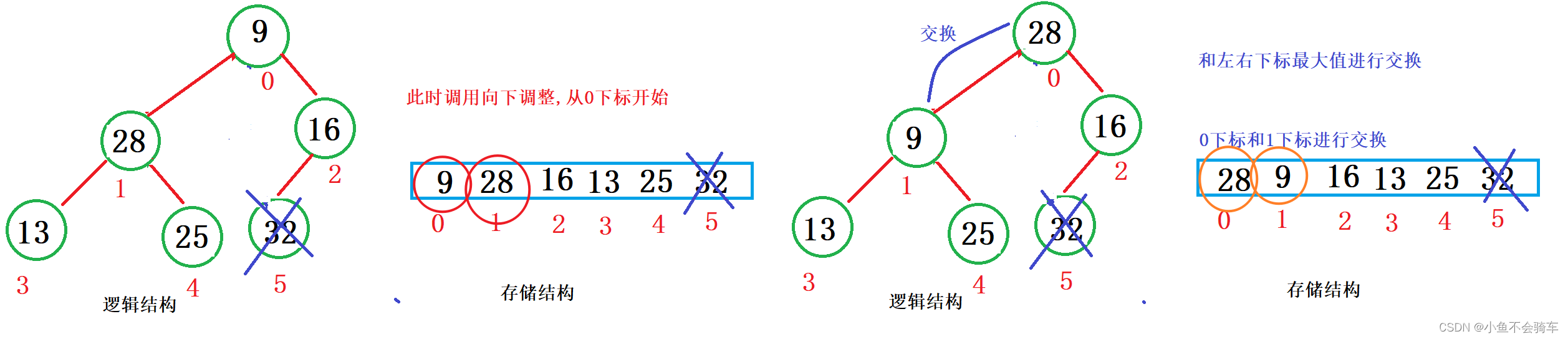
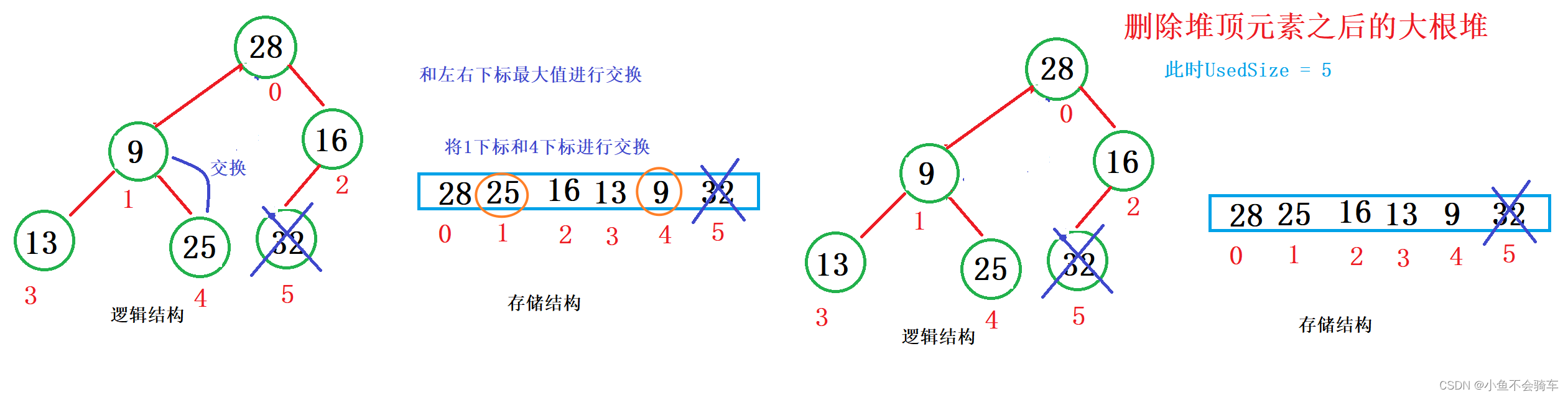
- 将堆顶元素对堆中最后一个元素交换
- 将堆中有效数据个数减少一个
- 对堆顶元素进行向下调整
我们看图:
代码入下:
/*** 删除* @return*/public int pop() {if(isEmpty()) {return -1;}int tmp = elem[0];//交换swap(elem,0,UsedSize-1);//元素个数-1UsedSize--;//调用向下调整,从0开始shiftDown(0,UsedSize);return tmp;}时间复杂度 : O(logN) 即树的高度
相关文章:

数据结构<堆>
🎇🎇🎇作者: 小鱼不会骑车 🎆🎆🎆专栏: 《数据结构》 🎓🎓🎓个人简介: 一名专科大一在读的小比特,努力学习编程是我唯一…...
Linux下Socket编程利用多进程实现一台服务器与多台客户端并发通信
文章目录前言一、服务器 server二、客户端 client三、并发通信演示四、程序源码前言 前些日子同“ Linux应用编程 ”专栏中发布过的TCP及UDP在Linux或Windows下的通信都为单进程下的Socket编程,若还存在一些套接字相关函数模糊不清,读者可移步“Socket编…...

【MySQL】数据库基础
目录 1、什么是数据库 2、 数据库基本操作 2.1 查看当前数据库 2.2 创建一个数据库 2.3 选中数据库 2.4 删除数据库 3、常见的数据类型 3.1 数值类型 3.2 字符串类型 3.3 日期类型 4、表的操作 4.1 创建表 4.2 查看指定数据库下的所有表 4.3 查看表的结构 4.…...

Microsoft Office 2021 / 2019 Direct Download Links
前言 微软Office在很长一段时间内都是最常用和最受欢迎的软件。从小型创业公司到大公司,它的使用比例相当。它可以很容易地从微软的官方网站下载。但是,微软只提供安装程序,而不提供完整的软件供下载。这些安装文件通常比较小。下载并运行后,安装的文件将从后端服务器安装M…...

XX 系统oracle RAC+ADG 数据库高可用容灾演练记录
停止备库监听,避免强制关机时切换到备库 su - grid lsnrctl stop 主库高可用重启测试 /u01/app/19c/grid/bin/crsctl stop crs sync;sync;reboot --/u01/app/19c/grid/bin/crsctl start crs 机器重启后自动起的 /u01/app/19c/grid/bin/crsctl stat res -t 主库容…...
JSP与Servlet
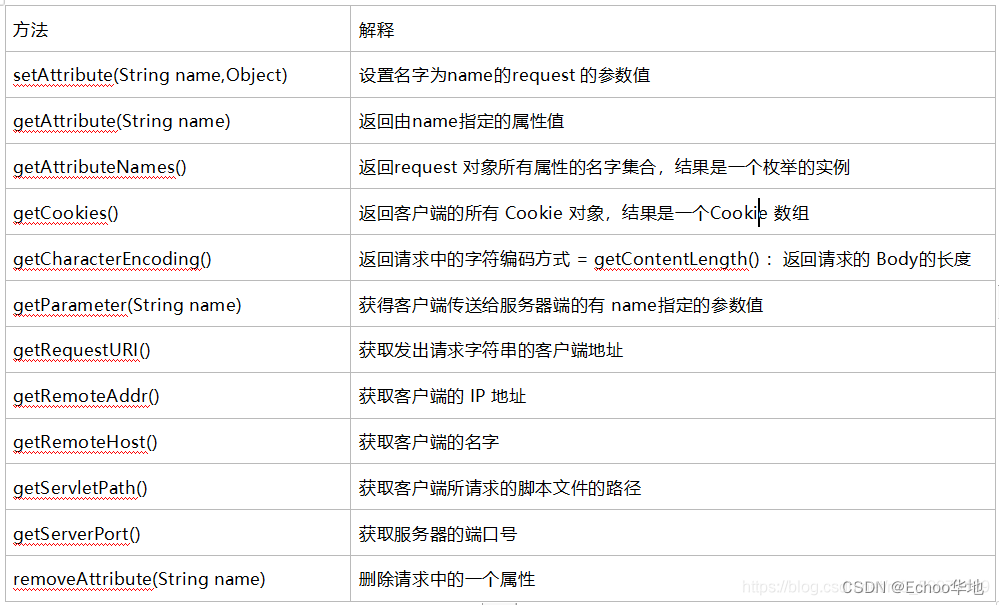
一、什么是JSP? JSP(java Service Pages)是由Sun Microsystems公司倡导、许多公司参与一起建立的动态技术标准。 在传统的HTML文件(*.htm 、 *.html)中加入Java程序片段(Scriptlet)和JSP标签,构成了JSP网页。 1.1 JSP页面的运行原理 客户…...
C++之迭代器
迭代器C中,迭代器就是类似于指针的对象,但比指针的功能更丰富,它提供了对对象的间接访问,每个迭代器对象代表容器中一个确定的地址。举个例子:void test() {vector<int> vv{1,2,3,4,5};for(vector<int>::i…...
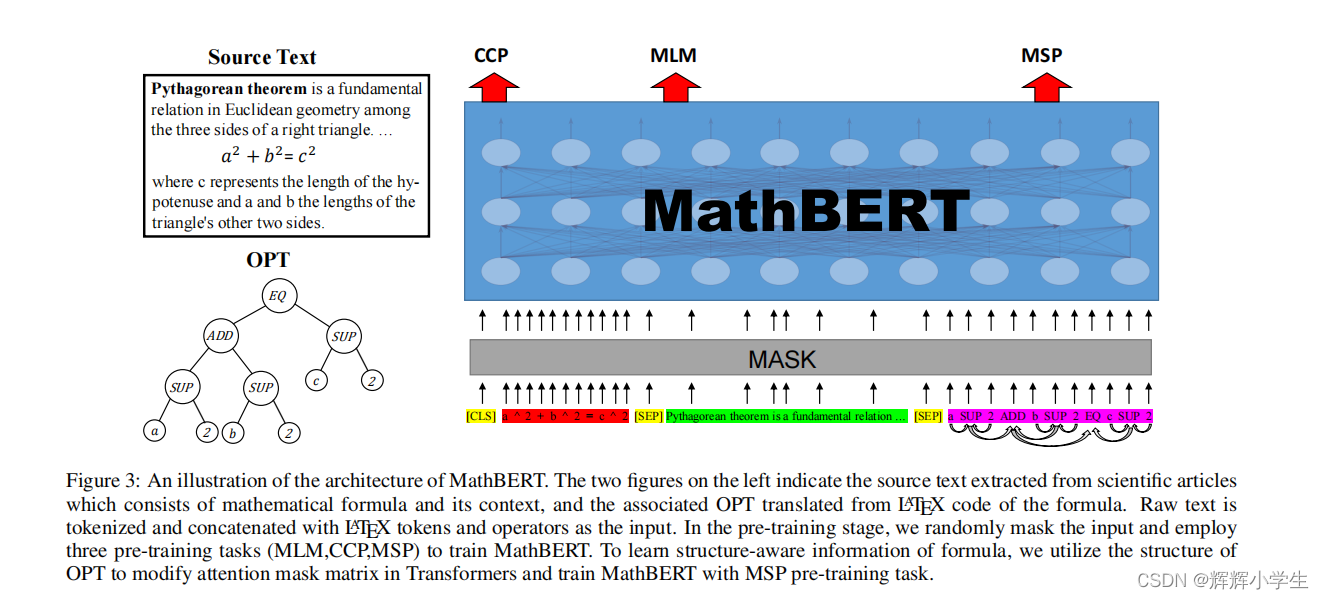
2023-02-16:干活小计
数学公式表示学习: 大约耗时:2 hours 在做了一些工作后重读论文:MathBERT: A Pre-Trained Model for Mathematical Formula Understanding 这是本篇论文最重要的idea:Current pre-trained models neglect the structural featu…...

Linux上安装LaTeX
Linux上安装LaTeX1. 安装1.1 下载安装texlive1.2 配置中文1.3 安装XeLatex1.4 安装编辑器1.5 设置默认支持中文编译1.6 配置环境路径2. latex配置2.1 latex自动安装宏包2.2 latex手动安装宏包2.2.1. 查找包2.2.2. 生成.sty文件2.2.3. 复制到配置文件夹3. 更新包3. 卸载参考链接…...
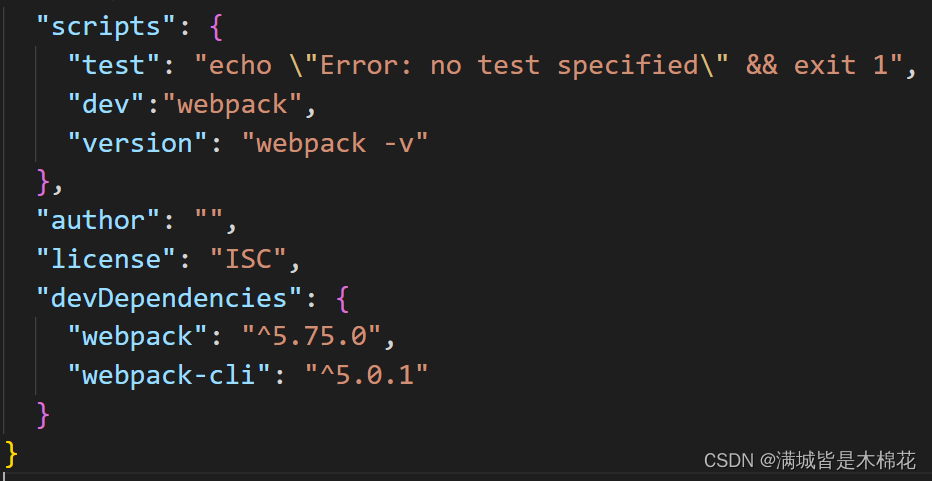
webpack -- 无法将“webpack”项识别为 cmdlet
webpack : 无法将“webpack”项识别为 cmdlet、函数、脚本文件或可运行程序的名称。请检查名称的拼写,如果包括路径,请确保路径正确,然后再试一次。 1.检测是否是版本太高而只能使用脚手架进行打包 webpack4.x的打包已经不能用webpack 文件a …...

对齐与非对齐访问
对齐与非对齐访问 什么是非对齐访问 在机器指令层面,当尝试从不能被 N 整除 (addr % N ! 0) 的起始地址读取 N 字节的数据时即发生了非对齐内存访问。举例而言,从地址 0x10004 读取 4 字节是可以的,然而从地址 0x10005 读取 4 字节数据将会…...
基于感知动作循环的层次推理用于视觉问答
title:Hierarchical Reasoning Based on Perception Action Cycle for Visual Question Answering 基于感知动作循环的层次推理用于视觉问答 文章目录title:[Hierarchical Reasoning Based on Perception Action Cycle for Visual Question Answering](…...

python中的.nc文件处理 | 05 NetCDF数据的进一步分析
NetCDF数据的进一步分析 比较不同数据集、不同季节的气候数据 import os import numpy as np import pandas as pd import matplotlib.pyplot as plt import cartopy.crs as ccrs import cartopy.feature as cfeature import seaborn as sns import geopandas as gpd import…...

GGX发布全新路线图,揭示具备 Layer0 特性且可编程的跨链基建生态
据彭博社报道,具备跨链通信且可编程的 Layer0 基础设施协议 Golden Gate (GGX) 已进行了 两年的线下开发,于近日公开发布了最新的路线图,该路线图不仅显示了该生态在过去两年的发展历程,也披露了 2023 年即将实现的重要里程碑。 G…...

taro+vue3 搭建一套框架,适用于微信小程序和H5
这里写tarovue3 搭建一套框架,适用于微信小程序和H5TaroVue3 搭建适用于微信小程序和 H5 的框架的大致步骤:TaroVue3 搭建适用于微信小程序和 H5 的框架的大致步骤: 安装 Taro。可以在终端输入以下命令进行安装: npm install -g…...

C++:模板初阶(泛型编程、函数模板、类模板)
文章目录1 泛型编程2 函数模板2.1 函数模板概念2.2 函数模板格式2.3 函数模板的原理2.4 函数模板的实例化2.5 模板参数的匹配原则3 类模板3.1 类模板的定义格式3.2 类模板的实例化1 泛型编程 所谓泛型,也就是通用型的意思。 在以往编写代码时,我们常常…...
)
把数组排成最小的数 AcWing(JAVA)
输入一个正整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。 例如输入数组 [3,32,321][3,32,321],则打印出这 33 个数字能排成的最小数字 321323321323。 数据范围 数组长度 [0,500][0,500]。 样例&#x…...
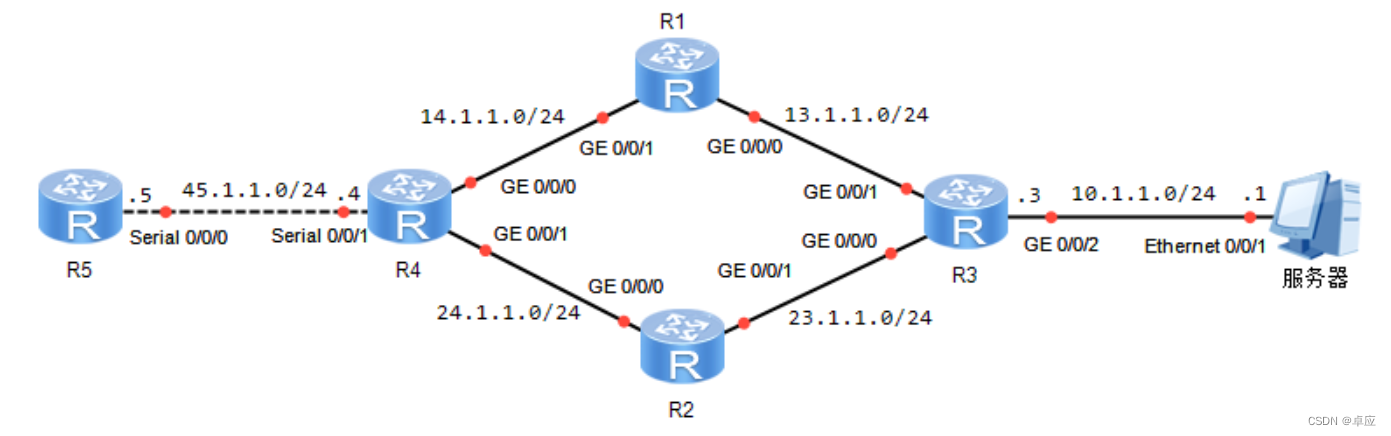
4.3 PBR
1. 实验目的 熟悉PBR的应用场景掌握PBR的配置方法2. 实验拓扑 PBR实验拓扑如图4-8所示: 图4-8:PBR 3. 实验步骤 (1) IP地址的配置 R1的配置 <Huawei>system-view...

hmac — 加密消息签名和验证
hmac — 加密消息签名和验证 1.概述 它的全称叫做Hash-based Message Authentication Code: 哈希消息认证码,从名字中就可以看出来这个hmac基于哈希函数的,并且还得提供一个秘钥key,它的作用就是用来保证消息的完整性,不可篡改。…...
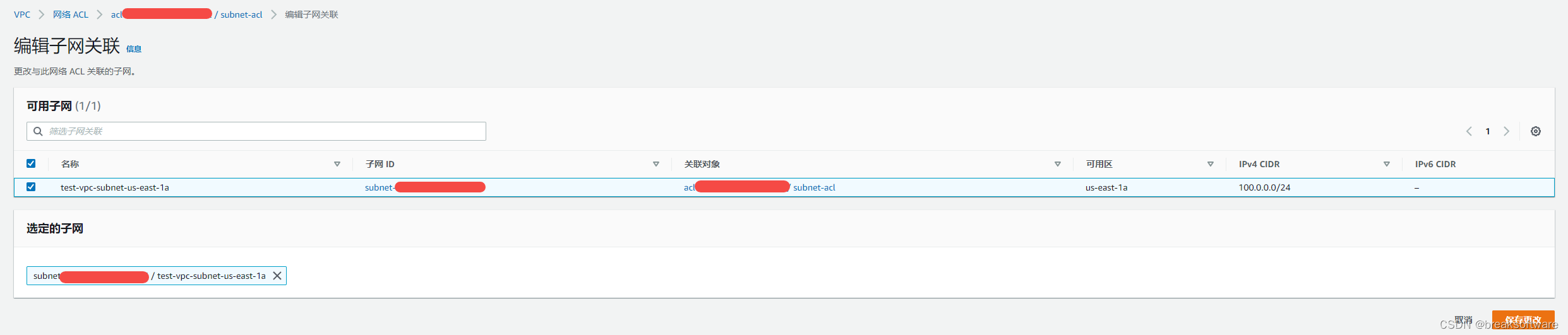
AWS攻略——使用ACL限制访问
文章目录确定出口IP修改ACL修改主网络ACL修改入站规则修改子网ACL创建子网ACL新增入站规则新增出站规则关联子网假如我们希望限制只有公司内部的IP可以SSH登录到EC2,则可以考虑使用ACL来实现。 我们延续使用《AWS攻略——创建VPC》的案例,在它的基础上做…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

