传染病模型
title: 传染病模型
date: 2023-7-24 10:55:00
updated: 2023-7-24 10:55:00
tags:
- 算法
- 数学建模
- 传染病模型
- matlab
categories: 数学建模
传染病模型中的符号表示


SI模型(艾滋传染模型)
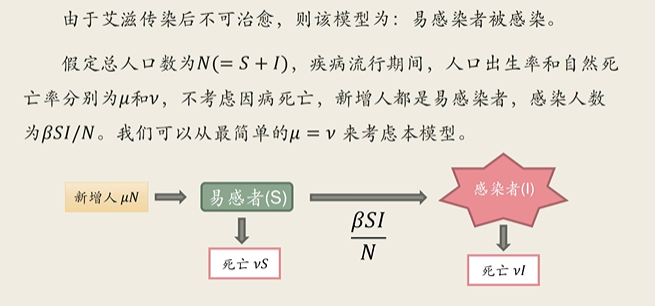
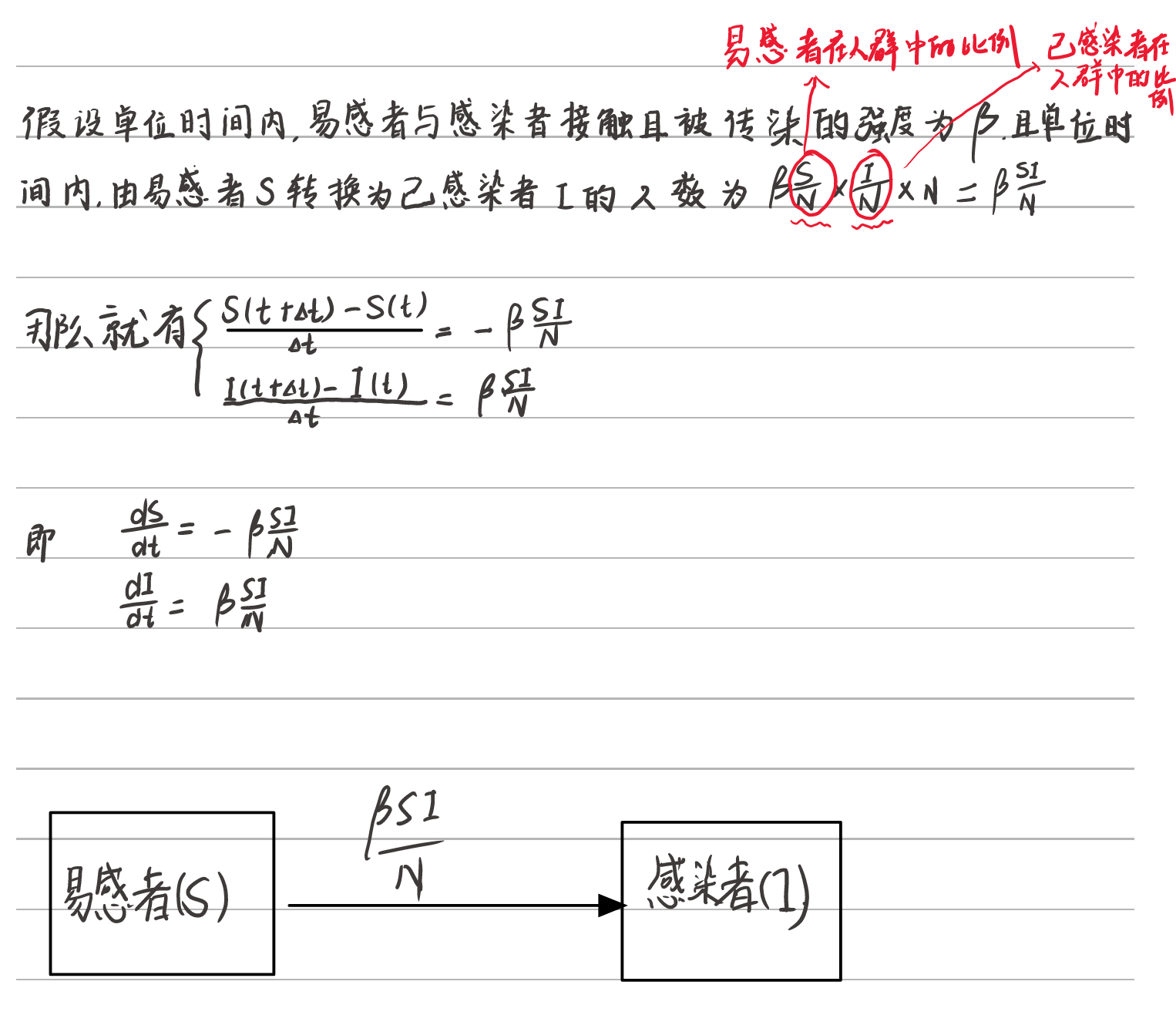
%% 直接求微分方程的解析解
dsolve('Dx1 = -0.1 * x1 * x2 / 1000', 'Dx2 = 0.1 * x1 * x2 / 1000','x1(0) = 999, x2(0) = 1', 't');%% 根据S + I = N做一个化简x1 = dsolve('Dx1 = -0.1 * x1 * (1000 - x1) / 1000', 'x1(0) = 999', 't');
x2 = 1000 - x1;figure(1)
fplot(x1, [0 200], 'b')
hold on
fplot(x2, [0 200], 'r')
legend('易感者', '感染者')%% 这道题目可以求出解析解,但是后面的大部分题目都是求不出解析解这里我们再熟悉一遍数值解的求解过程clc; clear
global TOTAL_N
TOTAL_N = 1000;
i0 = 1;
s0 = 999;
[t, x] = ode45('fun1', [1:200], [s0, i0]);
plot(t, x(:, 1), 'r-*');
hold on
plot(t, x(:, 2), 'b-+')'
legend('易感者', '感染者')
function dx = fun1(t, x)global TOTAL_Nbeta = 0.1;dx = zeros(2, 1);dx(1) = - beta * x(1) * x(2) / TOTAL_N;dx(2) = beta * x(1) * x(2) / TOTAL_N;
end
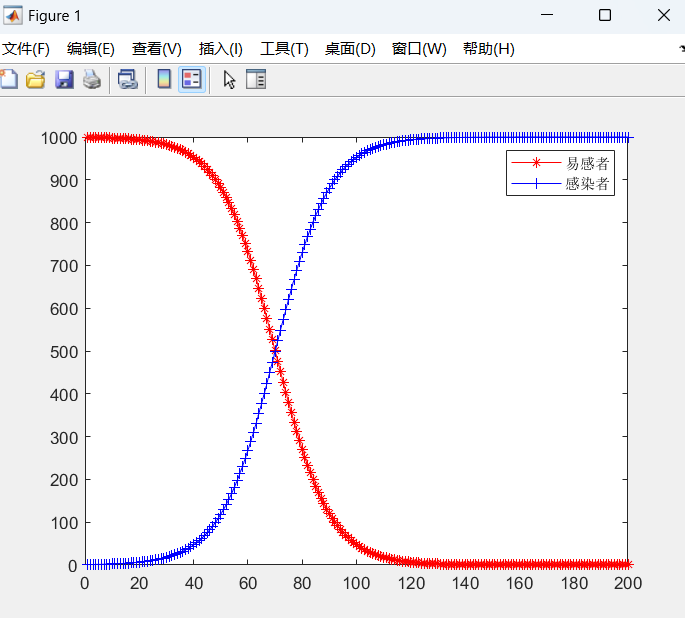
SIS模型(普通传染病模型 )

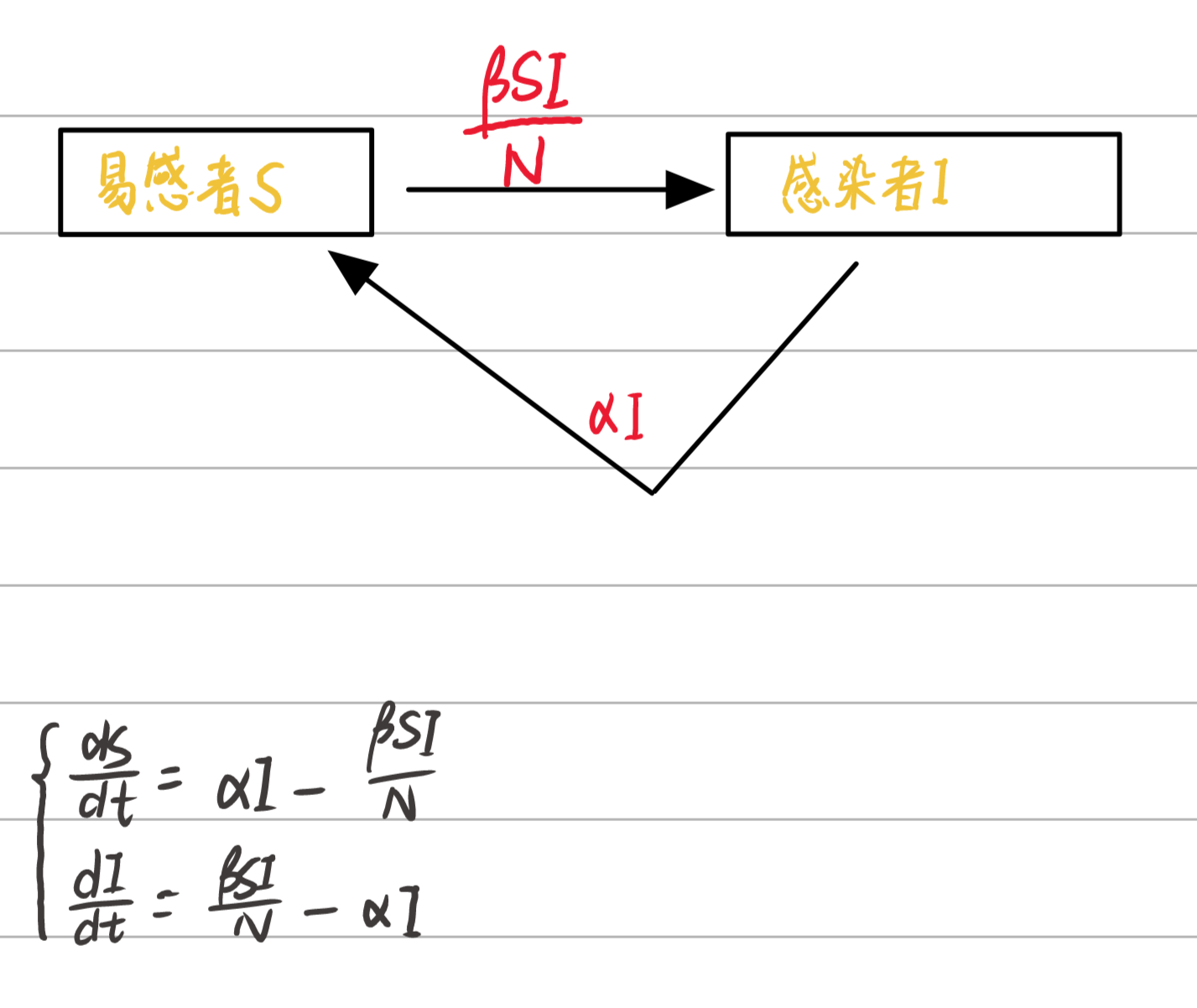
%%
clc;clear
global TOTAL_N
TOTAL_N = 1000;
global alfa;
alfa = 0.06;
global beta
beta = 0.1;
i0 = 1;
s0 = 999;
[t, x] = ode45('fun1', [1:500], [s0, i0]);
plot(t, x(:, 1), 'r-*');
hold on
plot(t, x(:, 2), 'b-+')'
legend('易感者', '感染者')
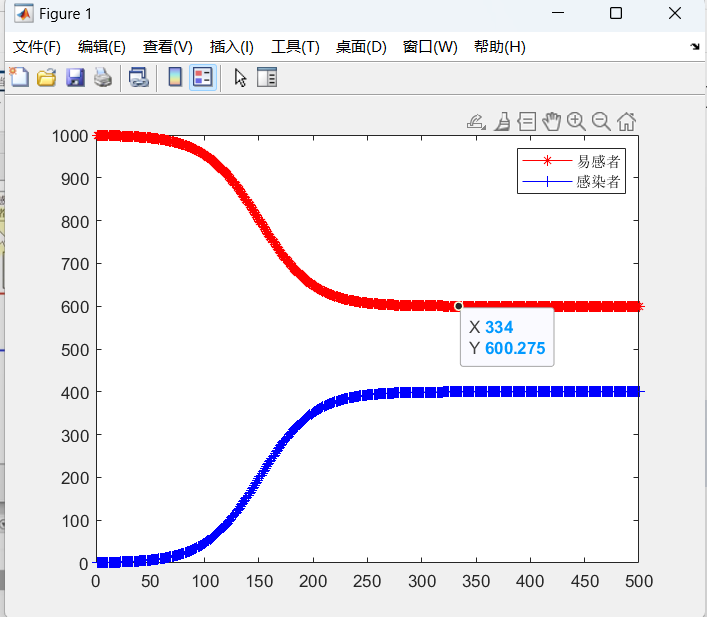
SIR模型

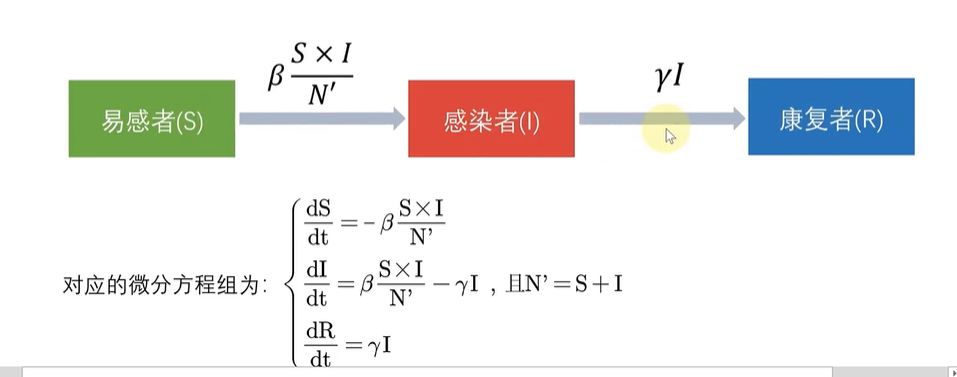
这里关于总人数毫无疑问 N = S + I + R但是在传染过程中,由于康复者已经有抗体且不会再被感染,所以这里有效人群就不能再把R计算在内了,N’ = S + I
%%
clc; clear all;
N = 1000;
i0 = 1;
s0 = 999;
r0 = 0;
[t, x] = ode45('fun1', [1:500], [s0 i0 0]);
x = round(x);
figure(1);
plot(t, x(:, 1), 'r-');
hold on
plot(t, x(:, 2), 'b-');
hold on
plot(t, x(:, 3), 'g-');
hold on
legend('易感者S','感染者I','康复者R')
function dx = fun1(t, x)beta = 0.1;gamma = 0.02;% x(1)表示S,x(2)表示I, x(3)表示Rdx = zeros(3,1);C = x(1) + x(2);dx(1) = - beta * x(1) * x(2) / C;dx(2) = beta * x(1) * x(2) / C - gamma * x(2);dx(3) = gamma * x(2);
end
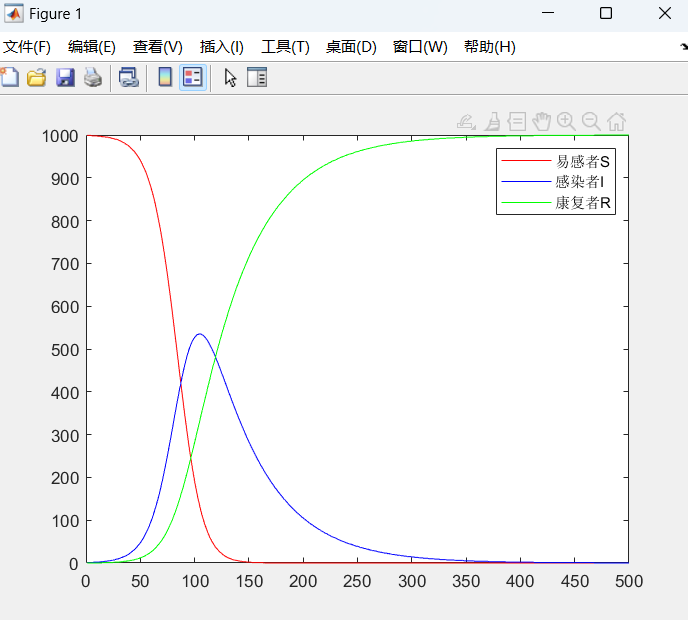
对SIR模型的拓展

function dx = fun1(t, x)beta = 0.1;gamma = 0.02;if t > 100gamma = gamma * 10;end% x(1)表示S,x(2)表示I, x(3)表示Rdx = zeros(3,1);C = x(1) + x(2);dx(1) = - beta * x(1) * x(2) / C;dx(2) = beta * x(1) * x(2) / C - gamma * x(2);dx(3) = gamma * x(2);
end
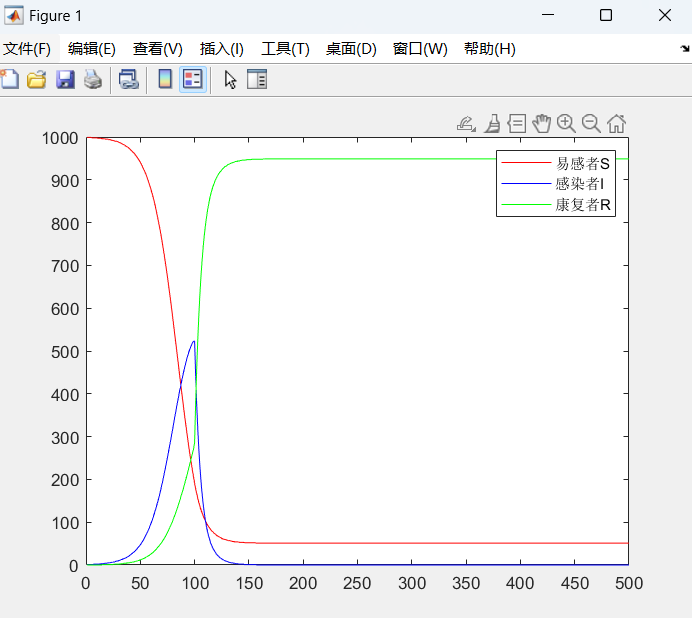
拓展2:考虑死亡率
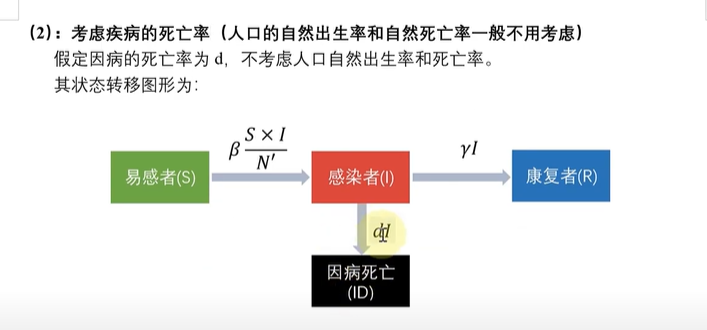
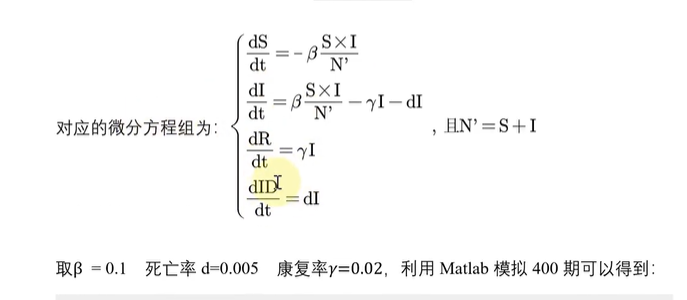
SIRS模型
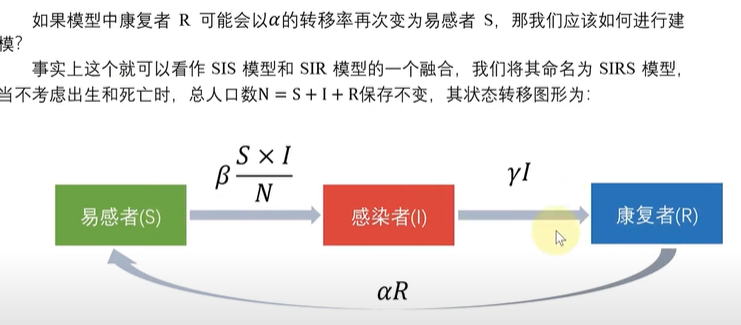

相关文章:

传染病模型
title: 传染病模型 date: 2023-7-24 10:55:00 updated: 2023-7-24 10:55:00 tags: 算法数学建模传染病模型matlab categories: 数学建模 传染病模型中的符号表示 SI模型(艾滋传染模型) %% 直接求微分方程的解析解 dsolve(Dx1 -0.1 * x1 * x2 / 1000, D…...
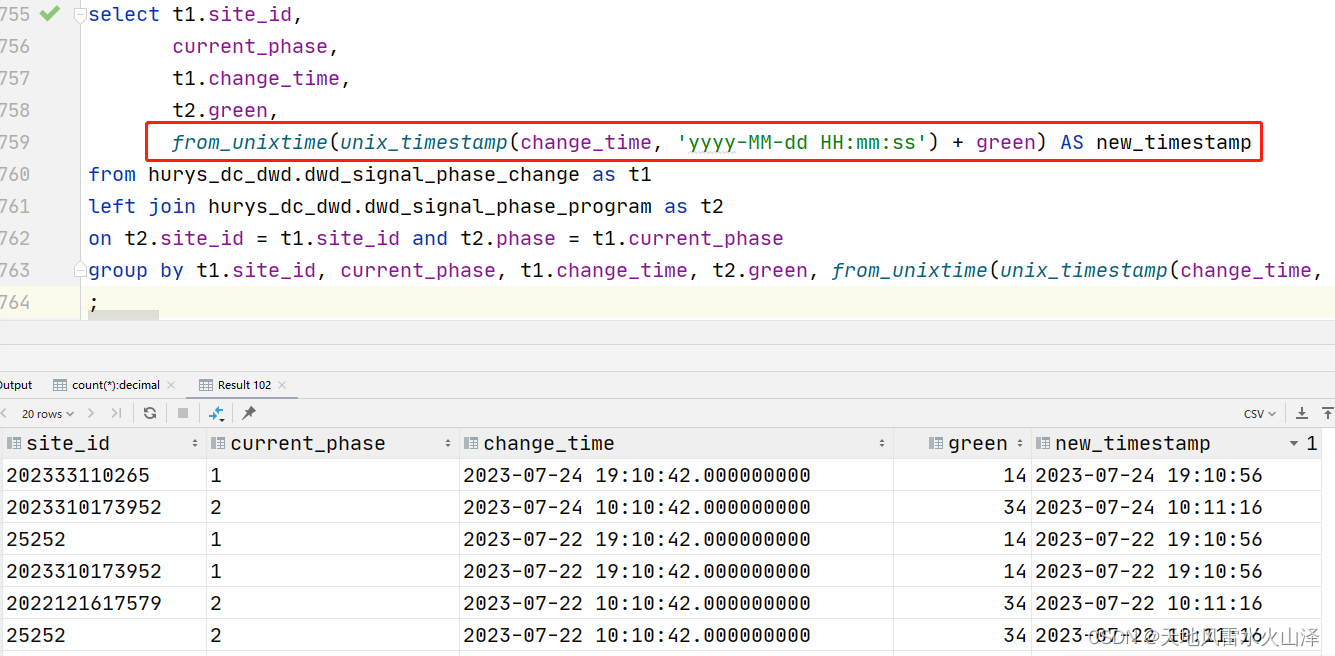
一百三十七、Hive——HQL运行报错(持续更新中)
一、timestamp字段与int字段相加 (一)场景 change_time字段是timestamp字段,代表一个红绿灯周期的开始时间(先是绿灯、再是黄灯、最后红灯),而green是int字段,代表绿灯的秒数,现在…...

Spring Boot配置加密实践
Spring Boot配置加密实践 使用Java技术栈的时候,Spring Boot几乎已经成为了标配。Spring Boot帮助我们简化了各种技术的整合,我们只需要在application.yml配置文件中增加一点点的配置即可。 虽然Spring Boot简化了我们的工作,但是也隐藏了底…...

SwiftUI-基础
应用入口 Main函数与App结构体的绑定,遵循App协议 main struct BaseApp: App {var body: some Scene {WindowGroup {ContentView()}} } 兼容UIApplicationDelegate main struct BasicApp: App {UIApplicationDelegateAdaptor(AppDelegate.self) var appDelegate…...

vue。cli怎么使用自定义组件,会有哪些问题
在Vue CLI中使用自定义组件的步骤如下: 通过仔细检查以上问题并按照正确的步骤使用自定义组件,大多数问题都可以解决。此外,查看开发者工具的控制台输出和Vue警告信息,可以帮助你进一步调试和解决可能出现的问题 创建自定义组件&a…...

linux----vim的使用
vi和vim是Linux下的一个文本编辑工具,最小化安装只有vi vim,需要额外安装,比vi更强大一些 # vim 操作文件,有三种模式:普通模式,编辑模式,命令模式 -vim 文件名刚进来----》普通模式--》只…...

95. Python基础教程:异常处理try...except语句
【目录】 文章目录 1. try...except语法解析2. 程序异常3. except的4种使用方式3.1 单独的except3.2 except 异常名称3.3 except 异常类型 as 别名3.4 except (异常类型1,异常类型2) as 别名 4. 总结 【正文】 1. try…except语法解析 try[traɪ]:尝试。 except[…...

详解rocketMq通信模块升级构想
本文从开发者的角度深入解析了基于netty的通信模块, 并通过简易扩展实现微服务化通信工具雏形, 适合于想要了解netty通信框架的使用案例, 想了解中间件通信模块设计, 以及微服务通信底层架构的同学。希望此文能给大家带来通信模块架构灵感。 概述 网络通信是很常见的需求&#…...

【BOOST程序库】对字符串的处理
基本概念这里不解释了,代码中详细解释了BOOST程序库中对于字符串每一个方法的详细用法: 注意:这里每实践一个方法,都将上面实践过的方法进行了注释,如果全部取消注释,会出现重命名的问题。 #include <…...
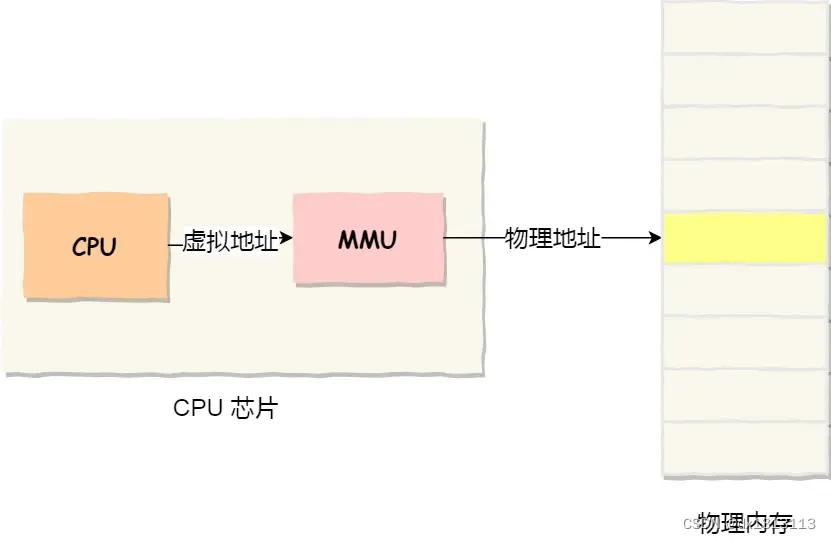
(学习笔记-内存管理)虚拟内存
单片机是没有操作系统的,每次写完代码,都需要借助工具把程序烧录进去,这样程序才能跑起来。另外,单片机的CPU是直接操作内存的[物理地址]。 在这种情况下,要想在内存中同时运行两个程序是不可能的。如果第一个程序在 2…...
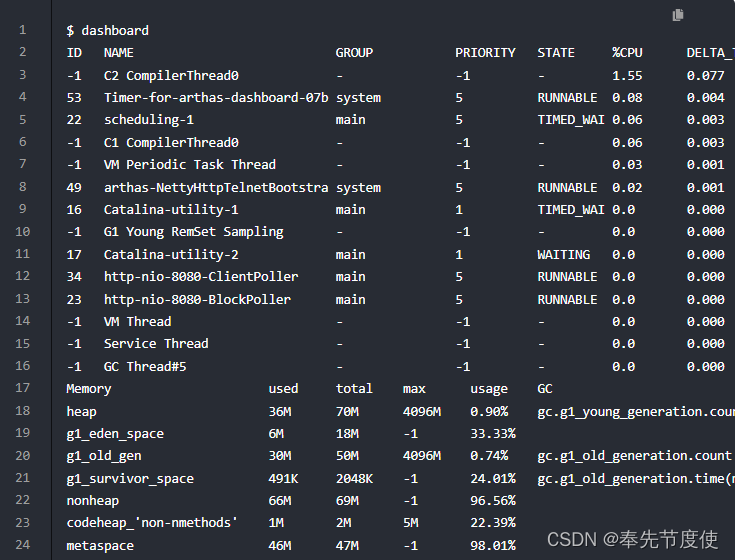
JVM理论(七)性能监控与调优
概述 性能优化的步骤 性能监控:就是通过以非强行或入侵方式收集或查看应用程序运行状态,包括如下问题 GC频繁CPU过载过高OOM内存泄漏死锁程序响应时间较长性能分析:通常在系统测试环境或者开发环境进行分析 通过查看程序日志以及GC日志,或者运用命令行工…...
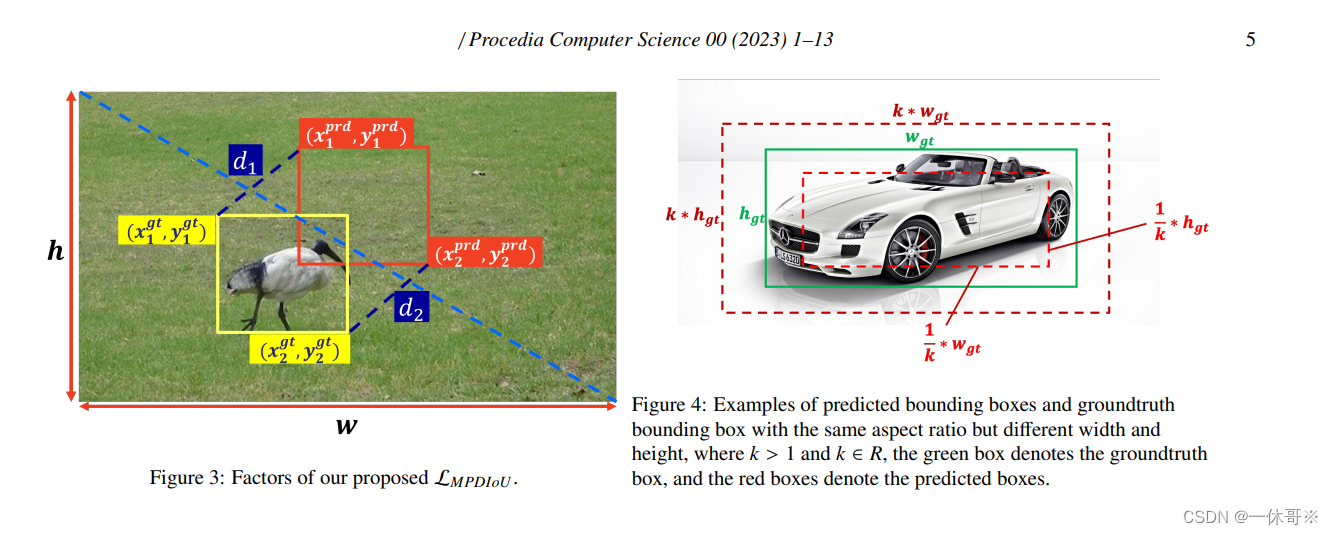
复现YOLOv8改进最新MPDIoU:有效和准确的边界盒回归的损失,打败G/E/CIoU,效果明显!!!
MPDIoU: A Loss for Efficient and Accurate Bounding Box Regression 论文简介MPDIoU核心设计思路论文方法实验部分加入YOLOv5代码论文地址:https://arxiv.org/pdf/2307.07662.pdf 论文简介 边界盒回归(Bounding box regression, BBR)广泛应用于目标检测和实例分割,是目标…...

LT6911C 是一款HDMI 1.4到双端口MIPIDSI/CSI或者LVDS加音频的一款高性能芯片
LT6911C 1.描述: LT6911C是一款高性能的HDMI1.4到MIPIDSI/CSI/LVDS芯片,用于VR/智能手机/显示器应用程序。对于MIPIDSI/CSI输出,LT6911C具有可配置的单端口或双端口MIPIDSI/CSI,具有1个高速时钟通道和1个~4个高速数据通道&#…...
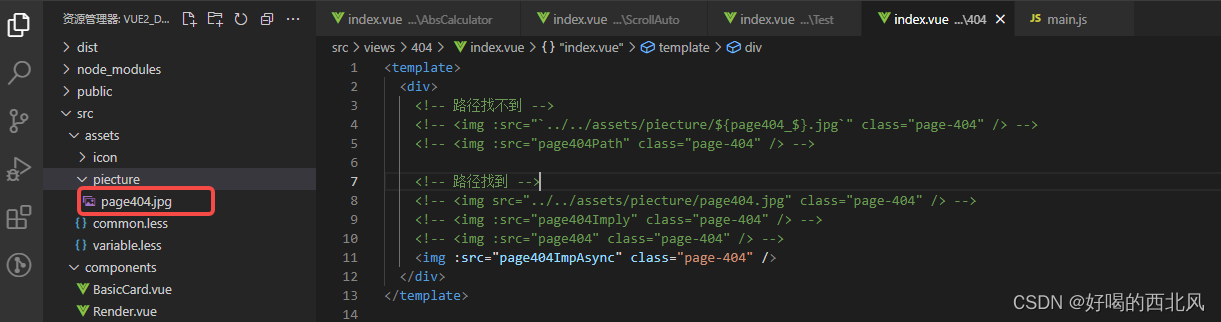
vue动态引入静态资源
vue动态引入静态资源 静态资源位置(../../assets/piecture/page404.jpg)或者(/assets/piecture/page404.jpg) 错误引入方式 错误引入方式(一) <template><div><img :src"../../asset…...

perl 强制覆盖拷贝文件
如果你想在Perl中进行文件拷贝时强制覆盖目标文件(如果目标文件已经存在),你可以使用标准模块File::Copy提供的cp函数,它允许你指定是否覆盖目标文件。 以下是一个示例,展示了如何在Perl中进行强制覆盖拷贝文件&#…...

C语言每日一题之整数求二进制1的个数
今天分享一道题目,用三种方法来求解 二进制1的个数 方法1 我们的十进制除10和取余数就可以得到我们每一位的数字,那我们的二进制也可 以 #include<stdio.h> int num_find_1(unsigned int n) {int count 0;while (n){if (1 n % 2){count;}n / 2…...

AcWing 4443.无限区域
原题链接:AcWing 4443.无限区域 题目来源:夏季每日一题2023 给定一个无限大的二维平面,设点 S 为该平面的中心点。 设经过点 S 的垂直方向的直线为 P,如果直线 P 是一个圆的切线,且切点恰好为点 S,那么&a…...
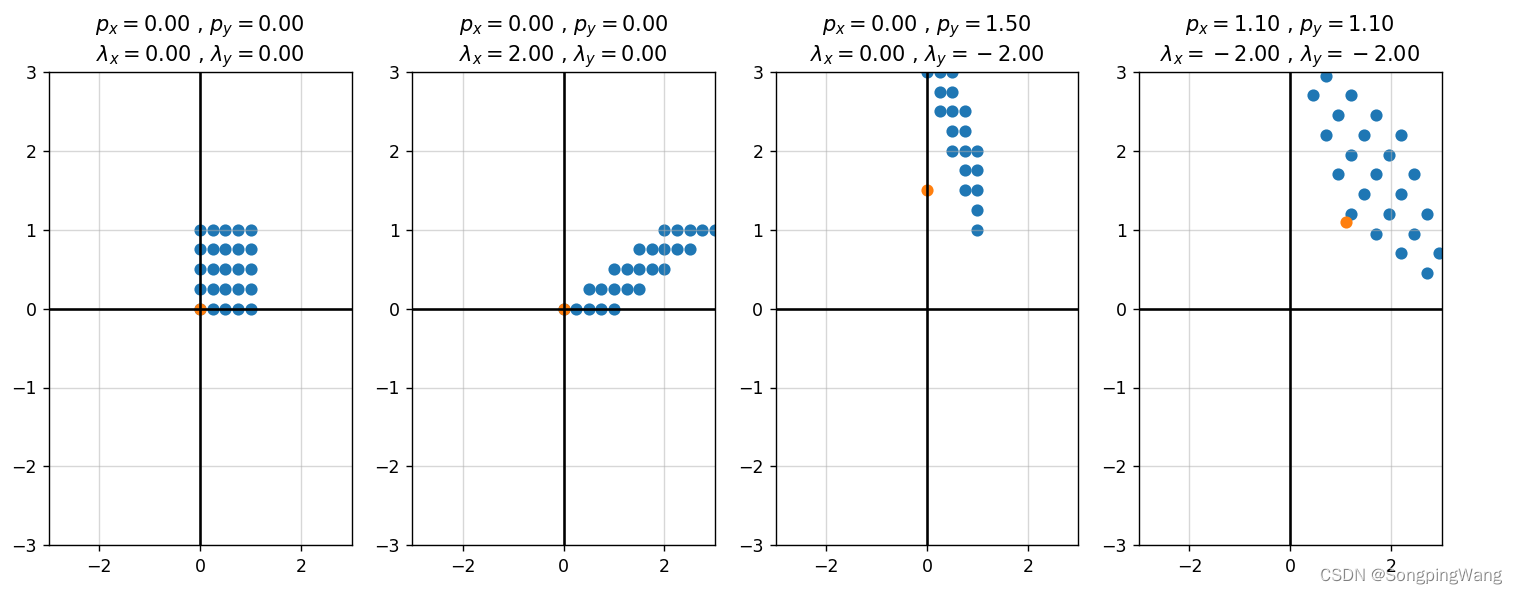
2D坐标系下的点的转换矩阵(平移、缩放、旋转、错切)
文章目录 1. 平移 (Translation)2. 缩放 (Scaling)3. 旋转 (Rotation)4. 错切 (Shearing)5. 镜像 (Reflection) 1. 平移 (Translation)…...

【Rabbitmq】报错:ERROR CachingConnectionFactory Channel shutdown: channel error;
报错内容 ERROR CachingConnectionFactory Channel shutdown: channel error; protocol method: #method<channel.close>(reply-code406, reply-textPRECONDITION_FAILED - unknown delivery tag 1, class-id60, method-id80) 原因 默认是自动ack,然后你代码…...

el-table组件的el-table-column电脑端使用fixed属性固定,移动端不使用固定,怎么实现?
要在电脑端使用 fixed 固定列,而在移动端不使用,可以使用 CSS 媒体查询结合 Vue 的动态绑定来实现。以下是一个示例代码: <template><el-table><el-table-columnprop"name"label"Name":fixed"isDesk…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...
