2D坐标系下的点的转换矩阵(平移、缩放、旋转、错切)
文章目录
- 1. 平移 (Translation)
- 2. 缩放 (Scaling)
- 3. 旋转 (Rotation)
- 4. 错切 (Shearing)
- 5. 镜像 (Reflection)
1. 平移 (Translation)
在2D空间中,我们经常需要将一个点平移到另一个位置。假设空间中的一点 P ( x , y ) P(x,y) P(x,y);将其向 x , y x, y x,y方向分别平移 t x t_x tx, t y t_y ty, 假设平移后点的坐标为 ( x ′ , y ′ ) (x',y') (x′,y′),则上述点的平移操作可以归纳为如下公式:
x ′ = x + t x y ′ = x + t y \begin{alignat}{2} &x'=x + t_x\\ &y'=x + t_y \end{alignat} x′=x+txy′=x+ty
使用齐次矩阵表示如下:
[ x ′ y ′ 1 ] = [ 1 b t x 0 1 t y 0 0 1 ] [ x y 1 ] \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & b & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} x′y′1 = 100b10txty1 xy1
import numpy as npdef translation():"""原始数组a 三个点(1,1) (4,4) (7,7)构建齐次矩阵 P构建变换矩阵 T"""a = np.array([[1, 1],[4, 4],[7, 7]])P = np.array([a[:, 0],a[:, 1],np.ones(len(a))])T = np.array([[1, 0, 2],[0, 1, 2],[0, 0, 1]])return np.dot(T, P)print(translation())"""
[[3. 6. 9.][3. 6. 9.][1. 1. 1.]]
"""
动画效果演示
import matplotlib
import matplotlib.pyplot as plt
import numpy as npX, Y = np.mgrid[0:1:5j, 0:1:5j]
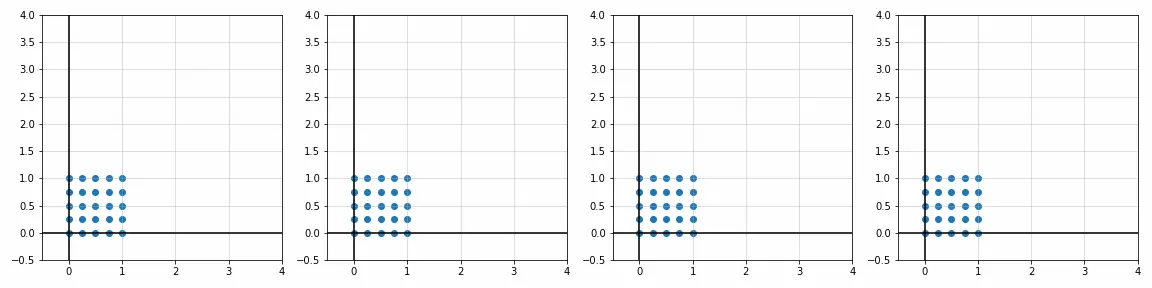
x, y = X.ravel(), Y.ravel()def trans_translate(x, y, tx, ty):T = [[1, 0, tx],[0, 1, ty],[0, 0, 1]]T = np.array(T)P = np.array([x, y, [1] * x.size])return np.dot(T, P)fig, ax = plt.subplots(1, 4)
T_ = [[0, 0], [2.3, 0], [0, 1.7], [2, 2]]
for i in range(4):tx, ty = T_[i]x_, y_, _ = trans_translate(x, y, tx, ty)ax[i].scatter(x_, y_)ax[i].set_title(r'$t_x={0:.2f}$ , $t_y={1:.2f}$'.format(tx, ty))ax[i].set_xlim([-0.5, 4])ax[i].set_ylim([-0.5, 4])ax[i].grid(alpha=0.5)ax[i].axhline(y=0, color='k')ax[i].axvline(x=0, color='k')
plt.show()
2. 缩放 (Scaling)
在2D空间中,点 ( x , y ) (x,y) (x,y)相对于另一点 ( p x , p y ) (p_x,p_y) (px,py)进行缩放操作,我们不妨缩放因子在 x , y x,y x,y方向分别为: s x , s y s_x, s_y sx,sy, 则上述的缩放操作可以归纳为如下公式:
x ′ = s x ( x − p x ) + p x = s x x + p x ( 1 − s x ) y ′ = s y ( y − p y ) + p y = s y y + p y ( 1 − s y ) \begin{alignat}{2} &x'=s_x(x-p_x) + p_x &=s_xx + p_x(1-s_x)\\ &y'=s_y(y-p_y) + p_y &=s_yy + p_y(1-s_y) \end{alignat} x′=sx(x−px)+pxy′=sy(y−py)+py=sxx+px(1−sx)=syy+py(1−sy)
使用齐次矩阵表示如下:
[ x ′ y ′ 1 ] = [ s x 0 p x ( 1 − s x ) 0 s y p y ( 1 − s y ) 0 0 1 ] [ x y 1 ] \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} s_x& 0 & p_x(1-s_x) \\ 0 & s_y& p_y(1-s_y)\\ 0 & 0& 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} x′y′1 = sx000sy0px(1−sx)py(1−sy)1 xy1
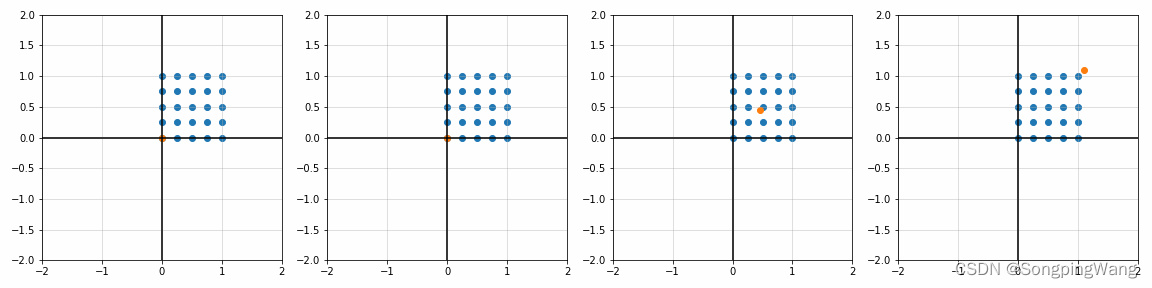
def trans_scale(x, y, px, py, sx, sy):T = [[sx, 0 , px*(1 - sx)],[0 , sy, py*(1 - sy)],[0 , 0 , 1 ]]T = np.array(T)P = np.array([x, y, [1]*x.size])return np.dot(T, P)fig, ax = plt.subplots(1, 4)
S_ = [[1, 1], [1.8, 1], [1, 1.7], [2, 2]]
P_ = [[0, 0], [0, 0], [0.45, 0.45], [1.1, 1.1]]
for i in range(4):sx, sy = S_[i]; px, py = P_[i]x_, y_, _ = trans_scale(x, y, px, py, sx, sy)ax[i].scatter(x_, y_)ax[i].scatter(px, py)ax[i].set_title(r'$p_x={0:.2f}$ , $p_y={1:.2f}$'.format(px, py) + '\n'r'$s_x={0:.2f}$ , $s_y={1:.2f}$'.format(sx, sy))ax[i].set_xlim([-2, 2])ax[i].set_ylim([-2, 2])ax[i].grid(alpha=0.5)ax[i].axhline(y=0, color='k')ax[i].axvline(x=0, color='k')plt.show()
3. 旋转 (Rotation)
在2D空间中,对点 ( x , y ) (x,y) (x,y)相对于另一点 ( p x , p y ) (p_x,p_y) (px,py)进行旋转操作,一般来说逆时针为正,顺时针为负,假设旋转角度为 β \beta β, 则上述点 x , y x,y x,y 相对于点 p x , p y p_x,p_y px,py的旋转角度 β \beta β 的操作使用齐次矩阵表示如下:
[ x ′ y ′ 1 ] = [ cos β − sin β p x ( 1 − cos β ) + p y sin β sin β cos β p y ( 1 − cos β ) + p x sin β 0 0 1 ] [ x y 1 ] \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} \cos \beta& -\sin \beta & p_x(1-\cos \beta) + p_y \sin \beta \\ \sin \beta & \cos \beta& p_y(1-\cos \beta) + p_x \sin \beta \\ 0 & 0& 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} x′y′1 = cosβsinβ0−sinβcosβ0px(1−cosβ)+pysinβpy(1−cosβ)+pxsinβ1 xy1
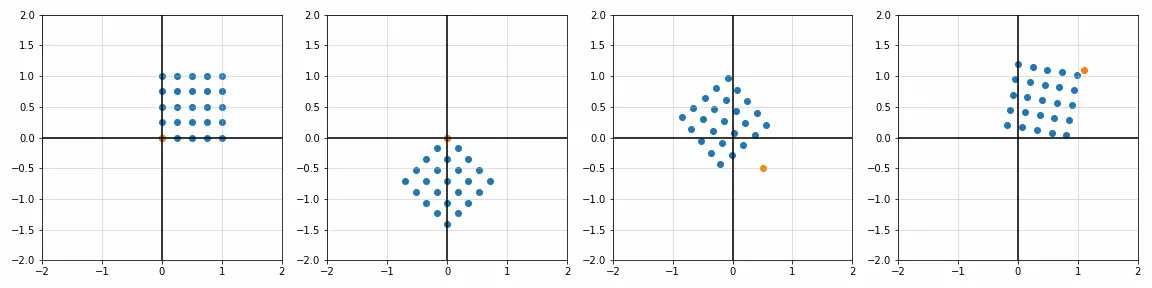
def trans_rotate(x, y, px, py, beta):beta = np.deg2rad(beta)T = [[np.cos(beta), -np.sin(beta), px*(1 - np.cos(beta)) + py*np.sin(beta)],[np.sin(beta), np.cos(beta), py*(1 - np.cos(beta)) - px*np.sin(beta)],[0 , 0 , 1 ]]T = np.array(T)P = np.array([x, y, [1]*x.size])return np.dot(T, P)fig, ax = plt.subplots(1, 4)R_ = [0, 225, 40, -10]
P_ = [[0, 0], [0, 0], [0.5, -0.5], [1.1, 1.1]]for i in range(4):beta = R_[i]; px, py = P_[i]x_, y_, _ = trans_rotate(x, y, px, py, beta)ax[i].scatter(x_, y_)ax[i].scatter(px, py)ax[i].set_title(r'$\beta={0}°$ , $p_x={1:.2f}$ , $p_y={2:.2f}$'.format(beta, px, py))ax[i].set_xlim([-2, 2])ax[i].set_ylim([-2, 2])ax[i].grid(alpha=0.5)ax[i].axhline(y=0, color='k')ax[i].axvline(x=0, color='k')plt.show()
4. 错切 (Shearing)
在2D空间中,对点 ( x , y ) (x,y) (x,y) 相对于另一点 ( p x , p y ) (p_x,p_y) (px,py)进行错切操作,错切一般用于弹性物体的变形处理。 假设沿x 方向与y方向错切参数分别为 λ x , λ y \lambda _x,\lambda _y λx,λy, 则的错切操作可以归纳使用齐次矩阵表示如下:
[ x ′ y ′ 1 ] = [ 1 λ x − λ x p x λ y 1 − λ y p y 0 0 1 ] [ x y 1 ] \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} 1& \lambda _x & -\lambda _x p_x \\ \lambda _y & 1& -\lambda _y p_y \\ 0 & 0& 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} x′y′1 = 1λy0λx10−λxpx−λypy1 xy1
import matplotlib.pyplot as plt
import numpy as npX, Y = np.mgrid[0:1:5j, 0:1:5j]
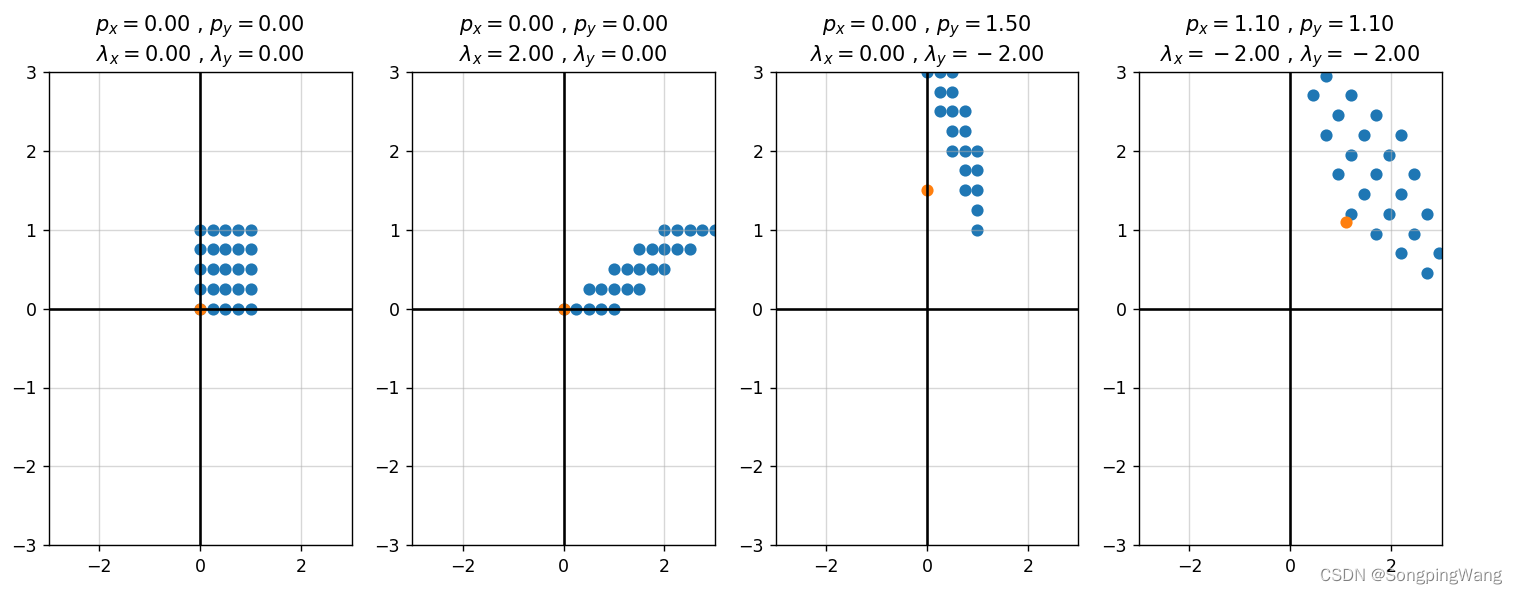
x, y = X.ravel(), Y.ravel()def trans_shear(x, y, px, py, lambdax, lambday):T = [[1 , lambdax, -lambdax*px],[lambday, 1 , -lambday*py],[0 , 0 , 1 ]]T = np.array(T)P = np.array([x, y, [1]*x.size])return np.dot(T, P)fig, ax = plt.subplots(1, 4)L_ = [[0, 0], [2, 0], [0, -2], [-2, -2]]
P_ = [[0, 0], [0, 0], [0, 1.5], [1.1, 1.1]]for i in range(4):lambdax, lambday = L_[i]; px, py = P_[i]x_, y_, _ = trans_shear(x, y, px, py, lambdax, lambday)ax[i].scatter(x_, y_)ax[i].scatter(px, py)ax[i].set_title(r'$p_x={0:.2f}$ , $p_y={1:.2f}$'.format(px, py) + '\n'r'$\lambda_x={0:.2f}$ , $\lambda_y={1:.2f}$'.format(lambdax, lambday))ax[i].set_xlim([-3, 3])ax[i].set_ylim([-3, 3])ax[i].grid(alpha=0.5)ax[i].axhline(y=0, color='k')ax[i].axvline(x=0, color='k')plt.show()
5. 镜像 (Reflection)
对于镜像,对称轴的法向量 v ( v x , v y ) v(v_x,v_y) v(vx,vy), 镜像矩阵 T m T_{m} Tm表示为:
[ 1 − 2 x v 2 − 2 x v y v 0 − 2 x v y v 1 − 2 y v 2 0 0 0 1 ] \left[ \begin{array}{ccc} 1-2 x_{v}{ }^{2} & -2 x_{v} y_{v} & 0 \\ -2 x_{v} y_{v} & 1-2 y_{v}{ }^{2} & 0 \\ 0 & 0 & 1 \end{array} \right] 1−2xv2−2xvyv0−2xvyv1−2yv20001
另外就是需要一个表示对称轴位置的点(对称轴2点中任意一点),表示为 M ( x m , y m ) M\left(x_{\mathrm{m}}, y_{m}\right) M(xm,ym),变换矩阵 H = T t ∗ T m ∗ T t − 1 H = T_{t}*T_{m}*T_{t}^{-1} H=Tt∗Tm∗Tt−1,即:
H = [ 1 0 0 0 1 0 x m y m 1 ] [ 1 − 2 x v 2 − 2 x v y v 0 − 2 x v y v 1 − 2 y v 2 0 0 0 1 ] [ 1 0 0 0 1 0 − x m − y m 1 ] H = \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ x_{\mathrm{m}} & y_{m} & 1 \end{array} \right] \left[ \begin{array}{ccc} 1-2 x_{v}{ }^{2} & -2 x_{v} y_{v} & 0 \\ -2 x_{v} y_{v} & 1-2 y_{v}{ }^{2} & 0 \\ 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -x_{\mathrm{m}} & -y_{m} & 1 \end{array} \right] H= 10xm01ym001 1−2xv2−2xvyv0−2xvyv1−2yv20001 10−xm01−ym001
镜像后的坐标即为 T o ∗ T t ∗ T m ∗ T t − 1 T_{o}*T_{t}*T_{m}*T_{t}^{-1} To∗Tt∗Tm∗Tt−1。
沿 X 轴 镜像的镜像矩阵:
[ 1 0 0 0 − 1 0 1 0 1 ] \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 1 & 0 & 1 \end{array} \right] 1010−10001
沿 Y 轴 镜像的镜像矩阵:
[ − 1 0 0 0 1 0 0 1 1 ] \left[ \begin{array}{ccc} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 1 \end{array} \right] −100011001
import numpy as npa = np.array([[1, 2],[2, 2],[3, 5],[4, 6]])
a = np.array([a[:,0], a[:,1], np.ones(len(a))])
print("\n",a)
print("--------------------------------")T_x = np.array( [[ 1, 0, 0],[ 0, -1, 0],[ 1, 0, 1]])
print("\n",np.dot(T_x, a))
print("=================================")
T_y = np.array( [[-1, 0, 0],[ 0, 1, 0],[ 0, 1, 1]])
print("\n",np.dot(T_y, a))
参考:
https://zhuanlan.zhihu.com/p/387578291
https://zhuanlan.zhihu.com/p/187411029
https://blog.csdn.net/Akiyama_sou/article/details/122144415
相关文章:

2D坐标系下的点的转换矩阵(平移、缩放、旋转、错切)
文章目录 1. 平移 (Translation)2. 缩放 (Scaling)3. 旋转 (Rotation)4. 错切 (Shearing)5. 镜像 (Reflection) 1. 平移 (Translation)…...

【Rabbitmq】报错:ERROR CachingConnectionFactory Channel shutdown: channel error;
报错内容 ERROR CachingConnectionFactory Channel shutdown: channel error; protocol method: #method<channel.close>(reply-code406, reply-textPRECONDITION_FAILED - unknown delivery tag 1, class-id60, method-id80) 原因 默认是自动ack,然后你代码…...

el-table组件的el-table-column电脑端使用fixed属性固定,移动端不使用固定,怎么实现?
要在电脑端使用 fixed 固定列,而在移动端不使用,可以使用 CSS 媒体查询结合 Vue 的动态绑定来实现。以下是一个示例代码: <template><el-table><el-table-columnprop"name"label"Name":fixed"isDesk…...
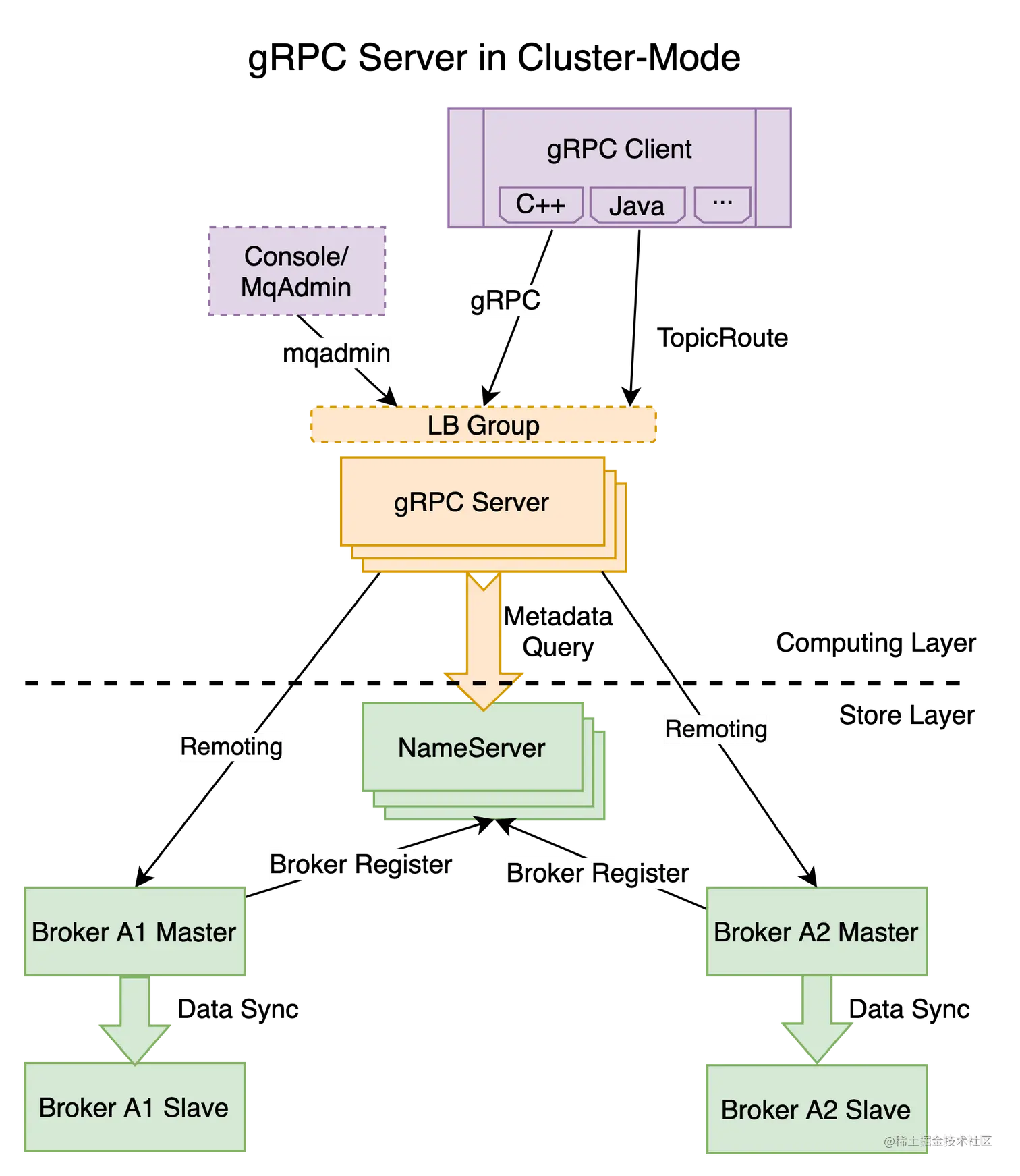
RocketMQ 行业分享
5.0的架构发生了重大调整,添加了一层rocketmq-proxy,可以通过grpc的方式接入。 参考 https://juejin.cn/post/7199413150973984827...

物联网场景中的边缘计算解决方案有哪些?
在物联网场景中,边缘计算是一种重要的解决方案,用于在物联网设备和云端之间进行实时数据处理、分析和决策。HiWoo Box作为工业边缘网关设备,具备边缘计算能力,包括单点公式计算、Python脚本编程以及规则引擎,它为物联网…...
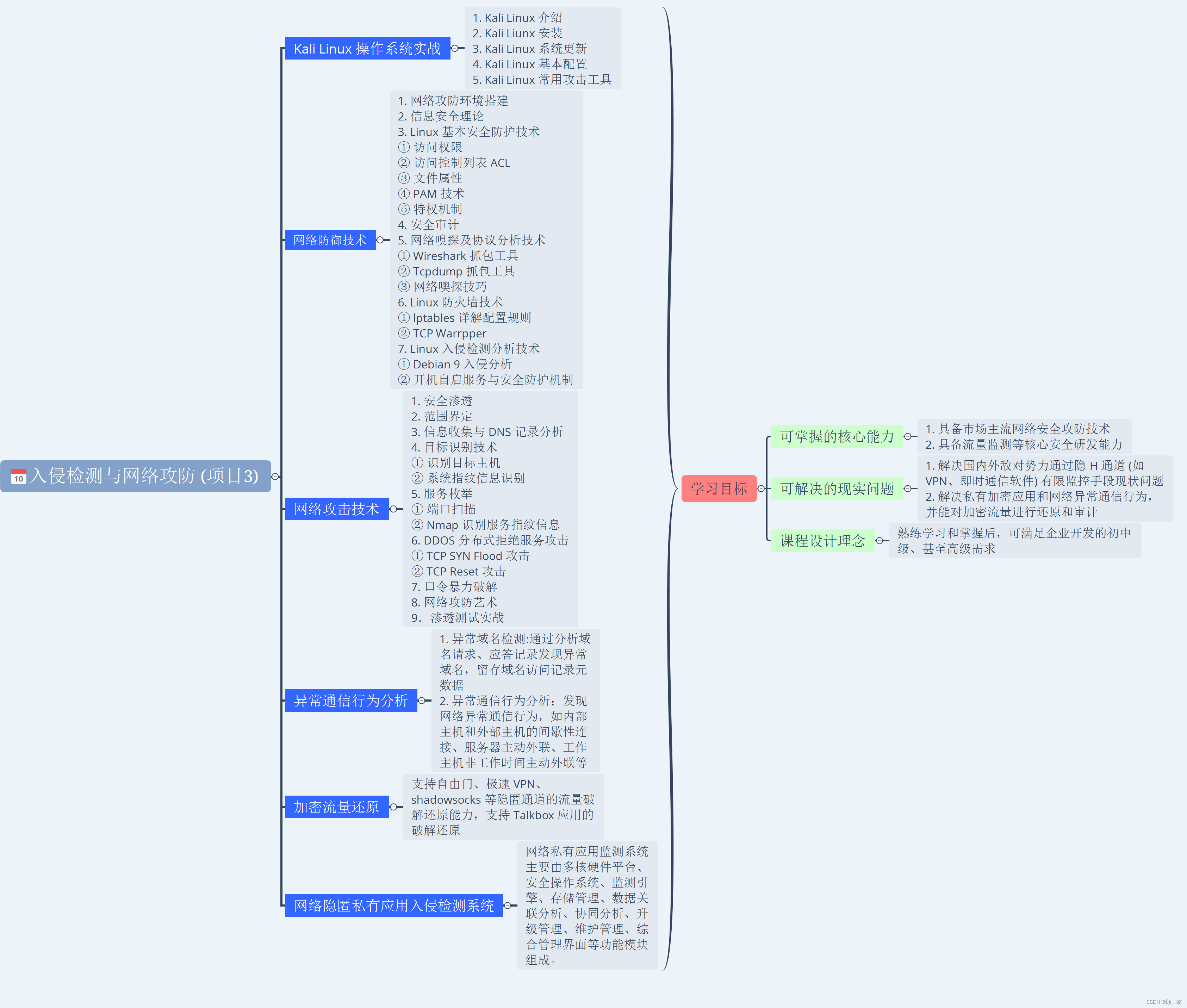
【C++ 进阶】学习导论:C/C++ 进阶学习路线、大纲与目标
目录 一、C 学习路线 二、C 课程大纲与学习目标 (1)第一阶段:C 语言基础 (2)第二阶段:C 高级编程 (3)第三阶段:C 核心编程与桌面应用开发 (4…...
【数据结构】实验七:字符串
实验七 字符串实验报告 一、实验目的与要求 1)巩固对串的理解; 2)掌握串的基本操作实现; 3)掌握 BF 和 KMP 算法思想。 二、实验内容 1. 给定一个字符串ababcabcdabcde和一个子串abcd,查找字串是否在主串中出现。…...

排序算法、
描述 由小到大输出成一行,每个数字后面跟一个空格。 输入 三个整数 输出 输入三个整数,按由小到大的顺序输出。 输入样例 1 2 3 1 输出样例 1 1 2 3 输入样例 2 4 5 2 输出样例 2 2 4 5 代码一(如下)࿱…...

rbd快照管理、rbd快照克隆原理与实现、rbd镜像开机自动挂载、ceph文件系统、对象存储、配置对象存储客户端、访问Dashboard
day04 day04快照快照克隆开机自动挂载ceph文件系统使用MDS对象存储配置服务器端配置客户端访问Dashborad 快照 快照可以保存某一时间点时的状态数据快照是映像在特定时间点的只读逻辑副本希望回到以前的一个状态,可以恢复快照使用镜像、快照综合示例 # 1. 在rbd存…...

vue、vuex、vue-router初学导航配合elementui及vscode快捷键
目录 一、vue资源 1.vue知识库汇总 2.vuejs组件 3.Vue.js 组件编码规范 目标 #目录 #基于模块开发...
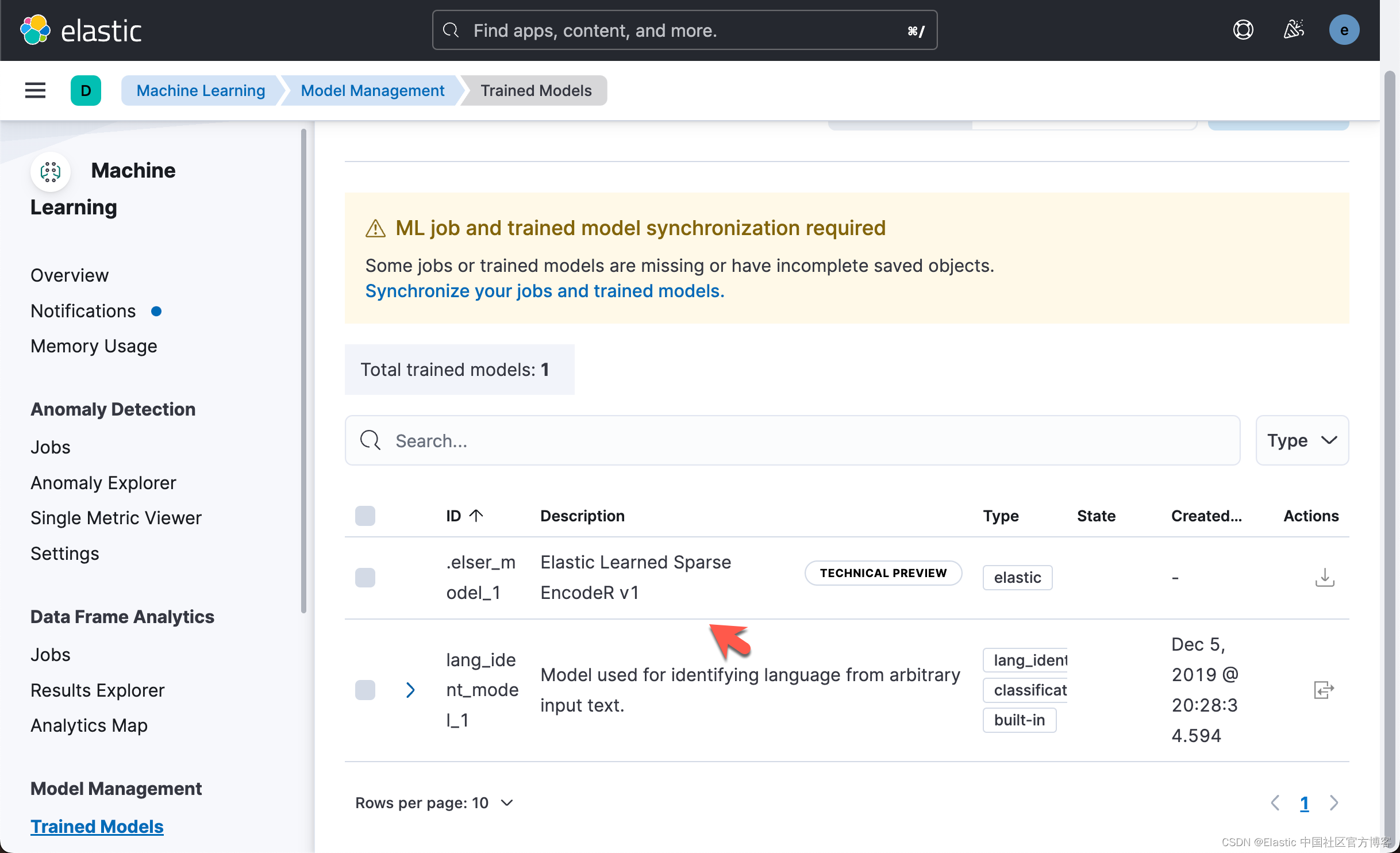
Elasticsearch:使用 ELSER 释放语义搜索的力量:Elastic Learned Sparse EncoderR
问题陈述 在信息过载的时代,根据上下文含义和用户意图而不是精确的关键字匹配来查找相关搜索结果已成为一项重大挑战。 传统的搜索引擎通常无法理解用户查询的语义上下文,从而导致相关性较低的结果。 解决方案:ELSER Elastic 通过其检索模型…...
MySQL数据库分库分表备份(shell脚本)
创建目录 mkdir /server/scripts 一、使用脚本实现分库备份 1、创建脚本并编写 [rootlocalhost scripts]# vim bak_db_v1.sh #!/bin/bash ######################################### # File Name:bak_db_v1.sh # Version: V1.0 # Author:Shen QL # Email:17702390000163.co…...

建造者设计模式go实现尝试
文章目录 前言代码结果总结 前言 本文章尝试使用go实现“建造者”。 代码 package mainimport ("fmt" )// 产品1。可以有不同的毫无相关的产品,这里只举一个 type Product1 struct {parts []string }// 产品1逻辑。打印组成产品的部分 func (p *Product…...

创建交互式用户体验:探索JavaScript中的Prompt功能
使用JavaScript中的Prompt功能:创建交互式用户体验 在前端开发中,JavaScript的prompt()函数是一个强大而有用的工具,它可以创建交互式的用户体验。无论是接收用户输入、进行简单的验证还是实现高级的交互功能,prompt()函数都能胜…...
-[提示模板:基础知识])
自然语言处理从入门到应用——LangChain:提示(Prompts)-[提示模板:基础知识]
分类目录:《自然语言处理从入门到应用》总目录 语言模型以文本作为输入,这段文本通常被称为提示(Prompt)。通常情况下,这不仅仅是一个硬编码的字符串,而是模板、示例和用户输入的组合。LangChain提供了多个…...

OpenPCDet调试出现的问题
Open3d遇到的问题,解决方案 1.ModuleNotFoundError: No module named ‘pcdet’ 原因:没有编译安装pcdet。 解决:进入openpcdet项目根目录,修改setup.py权限,并编译: sudo chmod 777 setup.py python set…...
【业务功能篇58】Springboot + Spring Security 权限管理 【下篇】
4.2.2.3 SpringSecurity工作流程分析 SpringSecurity的原理其实就是一个过滤器链,内部包含了提供各种功能的过滤器。这里我们可以看看入门案例中的过滤器。 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KjoRRost-1690534711077)(http…...

VBA技术资料MF34:检查Excel自动筛选是否打开
【分享成果,随喜正能量】聪明人,抬人不抬杠;傻子,抬杠不抬人。聪明人,把别人抬得很高,别人高兴、舒服了,看你顺眼了,自然就愿意帮你!而傻人呢?不分青红皂白&a…...

spring扩展点
在Spring框架中,有多个扩展点(Extension Point)可用于自定义和扩展应用程序的行为。这些扩展点允许开发人员介入Spring的生命周期和行为,并提供了灵活性和可定制性。以下是一些常见的Spring扩展点: BeanPostProcessor&…...

Skin Shader 使用自动生成的Thickness
Unity2023.2的版本,Thickness 自动化生成,今天测试了一把,确实不错。 1.Render 设置 在Project Settings->Graphics->HDRP Global Settings中 Frame Setting->Rendering->Compute Thickness 打开 2.Layer设置 2.1添加Layer&…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...
