【动态规划刷题 2】使⽤最⼩花费爬楼梯 解码⽅法
使⽤最⼩花费爬楼梯
746 . 使用最小花费爬楼梯
链接: 746 . 使用最小花费爬楼梯
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
示例 1:
输入:cost = [10,15,20]
输出:15
解释:你将从下标为 1 的台阶开始。
- 支付 15 ,向上爬两个台阶,到达楼梯顶部。
总花费为 15 。
示例 2:
输入:cost = [1,100,1,1,1,100,1,1,100,1]
输出:6
解释:你将从下标为 0 的台阶开始。
- 支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。
- 支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。
- 支付 1 ,向上爬一个台阶,到达楼梯顶部。
总花费为 6 。
1.状态表示
dp[i] 表示的是爬到第 i 阶楼梯时的最低花费。
2.状态转移方程
动态规划题,我们需要学会依靠经验和题目解析去猜测他们的状态转移方程。
爬到第i 阶位置,只有两种情况:
- 从 i-1 阶 爬一阶楼梯到 i;
- 从 i-2 阶 爬二阶楼梯到 i;
所以dp[i] 的值只需要 去其中的较小值即可,
dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
3. 初始化
从我们的递推公式可以看出, dp[i] 在 i = 0 以及 i = 1 的时候是没有办法进⾏推导的,因为dp[i-2] 或 dp[i-1] 不是⼀个有效的数据。
因此我们需要在填表之前,将0, 1的值初始化。题⽬中已经告诉我们
dp[0] = dp[1]=0
4. 填表顺序
按照数组下标的顺序,从左往右。
5. 返回值
应该返回 dp[n] 的值。
代码:
int minCostClimbingStairs(vector<int>& cost) {int n=cost.size();vector<int> dp(n+1);dp[0]=dp[1]=0;for(int i=2;i<=n;i++){dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[n];}
解码方法
91 . 解码方法
一条包含字母 A-Z 的消息通过以下映射进行了 编码 :
‘A’ -> “1”
‘B’ -> “2”
…
‘Z’ -> “26”
要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法)。例如,“11106” 可以映射为:
“AAJF” ,将消息分组为 (1 1 10 6)
“KJF” ,将消息分组为 (11 10 6)
注意,消息不能分组为 (1 11 06) ,因为 “06” 不能映射为 “F” ,这是由于 “6” 和 “06” 在映射中并不等价。
给你一个只含数字的 非空 字符串 s ,请计算并返回 解码 方法的 总数 。
题目数据保证答案肯定是一个 32 位 的整数。
示例 1:
输入:s = “12”
输出:2
解释:它可以解码为 “AB”(1 2)或者 “L”(12)。
示例 2:
输入:s = “226”
输出:3
解释:它可以解码为 “BZ” (2 26), “VF” (22 6), 或者 “BBF” (2 2 6) 。
示例 3:
输入:s = “06”
输出:0
解释:“06” 无法映射到 “F” ,因为存在前导零(“6” 和 “06” 并不等价)。
1.状态表示
dp[i] 表示的是以第i位置为结尾时的解码方法数。
2.状态转移方程
动态规划题,我们需要学会依靠经验和题目解析去猜测他们的状态转移方程。
以 i-1 的位置进行分析,有两种情况:
- i位置是的数字在 1~9 之间,能单独表示一个字母
- i和i-1 位置的数字可以组成一个在 10 ~ 26 之间的一个字母
所以
i. 当 s[i] 上的数在 [1, 9] 区间上时: dp[i] += dp[i - 1] ;
ii. 当 s[i - 1] 与 s[i] 上的数结合后,在 [10, 26] 之间的时候: dp[i] +=dp[i - 2] ;
3. 初始化
从我们的递推公式可以看出, dp[i] 在 i = 0 以及 i = 1 的时候是没有办法进⾏推导的,因为dp[i-2] 或 dp[i-1] 不是⼀个有效的数据。
因此我们需要在填表之前,将0, 1的值初始化。
- 当s[0]不为‘0’ 时,dp[0]=1; 否则,dp[0]=0;
- 当s[1]!=‘0’ 时,dp[1]+=1; 当 s[0] 与 s[1] 上的数结合后,在 [10, 26] 之间的时,dp[1]+=1;
4. 填表顺序
按照数组下标的顺序,从左往右。
5. 返回值
应该返回 dp[n-1] 的值。
代码
int numDecodings(string s) {//动态规划//创建dp[]数组//初始化//填表//返回值int n=s.size();vector<int> dp(n);//初始化if(s[0]=='0') return 0;dp[0]=1;if(n==1) return dp[0];if(s[1]!='0') dp[1]+=1;int t= (s[0]-'0')*10+s[1]-'0';if(t>=10&&t<=26){dp[1]+=1;}for(int i=2;i<n;i++){if(s[i]!='0') dp[i]+=dp[i-1];int t= (s[i-1]-'0')*10+s[i]-'0';if(t>=10&&t<=26){dp[i]+=dp[i-2];}}return dp[n-1];
}
相关文章:

【动态规划刷题 2】使⽤最⼩花费爬楼梯 解码⽅法
使⽤最⼩花费爬楼梯 746 . 使用最小花费爬楼梯 链接: 746 . 使用最小花费爬楼梯 给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。 你可以选择从下标为 0 或下标为 …...

Python的基本语法
“有人说,写python就像是坐在一个没有安全带的车上, 我认为这个说法很欠妥当, 应该是一辆没有外壳和座椅, 只有发动机和轮子的车, 并且车上摆满了轮子” python既然是作为一个工具,那么就不需要去深入…...

Kubernetes那点事儿——存储之存储卷
Kubernetes那点事儿——存储之存储卷 前言一、K8s数据卷一、临时存储卷emptyDir二、节点存储卷hostPath三、网络存储NFS 前言 在K8s中用Volume为容器提供了外部的存储能力。 Pod需要设置卷来源(spec.volume)和挂载点(spec.containers.volumeM…...

Go语言中‘String’包中的‘Cut‘函数的实现
Go语言中‘String’包中的’Cut’函数的实现 Cut函数用于在字符串**‘s’中查找子串’sep’,并将字符串’s’在子串 ‘sep’ 第一次出现的位置分割成两部分:before和after** package main import("fmt" "strings" ) func main(…...
【JAVASE】顺序和选择结构
⭐ 作者:小胡_不糊涂 🌱 作者主页:小胡_不糊涂的个人主页 📀 收录专栏:浅谈Java 💖 持续更文,关注博主少走弯路,谢谢大家支持 💖 顺序和选择 1. 顺序结构2. 分支结构2.1 …...

Oracle恢复删除的数据
不下心删除了生产库的数据或者不小心删除了一部分数据,如何恢复找回。 Oracle恢复删除数据的方法 方案一 利用oracle提供的闪回方法进行数据恢复,适用于delete删除方式 首先获取删除数据的时间点: select * from v$sql where sql_text l…...

(无人机方向)ros小白之键盘控制无人机(终端方式)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一:配置pycharm的ros开发环境二:核心代码讲解三 效果演示XTDrone 四 完整代码 前言 ubuntu 18.04 pycharm ros melodic 做一个在终端中…...

【python学习笔记】argparse --- 命令行选项、参数和子命令解析器
argparse 是 Python 的标准库中的一个模块,用于解析命令行参数。它提供了一种简单而灵活的方式来处理命令行输入,并生成易于使用的帮助文档。 使用 argparse 模块可以轻松地定义命令行参数和选项,并自动生成用法帮助和错误消息。示例&#x…...

【Java框架】RPC远程调用
RPC架构 一、RPC概述 RPC(Remote Procedure Call)叫作远程过程调用,它是利用网络从远程计算机上请求服务,可以理解为把程序的一部分放在其他远程计算机上执行。通过网络通信将调用请求发送至远程计算机后,利用远程计…...

云原生全栈体系(一)
云平台核心 第一章 为什么用云平台 环境统一按需付费即开即用稳定性强 一、国内常见云平台 阿里云、百度云、腾讯云、华为云、青云… 二、国外常见云平台 亚马逊 AWS、微软 Azure … 三、公有云 购买云服务商提供的公共服务器 公有云是最常见的云计算部署类型。公有云资…...
【【51单片机直流电机调速】】
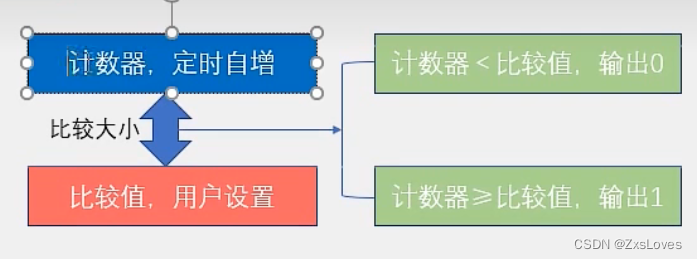
学会电机调速,掌握中国速度 PWM的生成方法 先用户设定一个比较值,然后计数器定时自增。 当计数器<比较值,输出0 当计数器>比较值,输出1 main.c #include <REGX52.H> #include"delay.h" #include"…...

【Spring Boot】
目录 🍪1 Spring Boot 的创建 🎂2 简单 Spring Boot 程序 🍰3 Spring Boot 配置文件 🍮3.1 properties 基本语法 🫖3.2 yml 配置文件说明 🍭3.2.1 yml 基本语法 🍩3.3 配置文件里的配置类…...
使用docker 部署自己的chatgpt
直接docker部署 docker run --name chatgpt-web -d -p 3002:3002 --env OPENAI_API_KEYyour_api_key chenzhaoyu94/chatgpt-web:latestDocker compose部署 version: 3services:app:image: chenzhaoyu94/chatgpt-web # 总是使用 latest ,更新时重新 pull 该 tag 镜像即可ports…...

Python适配器模式介绍、使用方法
一、Python适配器模式介绍 适配器模式(Adapter Pattern) 是一种结构型设计模式,用于将不兼容的接口转换为另一种接口,以便系统间的协同工作。 功能: 适配器模式主要功能是将一个类的接口转换成客户端所期望的另一种接口,以满足…...
【数据结构】复杂度
🔥博客主页:小王又困了 📚系列专栏:数据结构 🌟人之为学,不日近则日退 ❤️感谢大家点赞👍收藏⭐评论✍️ 目录 一、什么是数据结构 二、什么是算法 三、算法的效率 四、时间复杂度 4.…...

【读点论文】PP-YOLOE: An evolved version of YOLO,面向友好部署的模型设计,为项目后续产业落地提供了更加有效的参考
PP-YOLOE: An evolved version of YOLO Abstract 在本报告中,我们介绍了PP-YOLOE,一种具有高性能和友好部署的工业最先进的目标探测器。我们在之前的PP-YOLOv2的基础上进行优化,采用无锚模式,更强大的骨干和颈部配备CSPRepResSt…...

微服务入门---SpringCloud(二)
微服务入门---SpringCloud(二) 1.Nacos配置管理1.1.统一配置管理1.1.1.在nacos中添加配置文件1.1.2.从微服务拉取配置 1.2.配置热更新1.2.1.方式一1.2.2.方式二 1.3.配置共享1)添加一个环境共享配置2)在user-service中读取共享配置…...

51单片机IO口控制
51单片机IO口控制 1.点亮LED灯 原理:根据电路图,指向IO口的引脚;拉低电平,灯亮、 如图: [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Zfco4IjK-1690308697530)(C:/Users/xie19/Pictur…...
ERROR 1064 - You have an error in your SQL syntax;
ERROR 1064 - You have an error in your SQL syntax; check the manual that corresponds to your MySQL server version for the right syntax to use near (/, 少个逗号吧,以前开始写SQL,特别是修改SQL的时候容易出现这样错误。 而且自己也知道在附近…...

leetcode做题笔记46
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 思路一:回溯 void swap(int *nums,int index1,int index2) {int temp nums[index1];nums[index1] nums[index2];nums[index2] temp; }void prem(int* nu…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...
