leetcode做题笔记46
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
思路一:回溯
void swap(int *nums,int index1,int index2)
{int temp = nums[index1];nums[index1] = nums[index2];nums[index2] = temp;
}void prem(int* nums, int numsSize, int* returnSize, int** returnColumnSizes,int** returnNums,int offset)
{if(offset == numsSize){returnNums[*returnSize] = (int *)malloc(sizeof(int ) * numsSize);memcpy(returnNums[*returnSize],nums,sizeof(int) * numsSize );(*returnColumnSizes)[*returnSize] = numsSize;*returnSize = *returnSize + 1;}else{int i;for(i = offset; i < numsSize; i++){swap(nums,i,offset);prem(nums,numsSize,returnSize,returnColumnSizes,returnNums,offset+1);swap(nums,i,offset);}}
}int** permute(int* nums, int numsSize, int* returnSize, int** returnColumnSizes)
{int **returnNums = (int **)malloc(sizeof(int *) * 721);*returnColumnSizes= (int *)malloc(sizeof(int ) * 721);*returnSize = 0;prem(nums,numsSize,returnSize,returnColumnSizes,returnNums,0);return returnNums;}分析:
本题考虑到要列举所有可能的情况,故考虑使用回溯算法。编写prem函数来进行回溯,当遍历到末尾时申请一个新的空间来存放新的情况,否则就将i和offset交换。不断将新的情况的值赋给新的数组。最后输出数组。
总结:
本题考察了回溯算法的应用,要将回溯的各种情况考虑清楚后方能解决。
相关文章:

leetcode做题笔记46
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 思路一:回溯 void swap(int *nums,int index1,int index2) {int temp nums[index1];nums[index1] nums[index2];nums[index2] temp; }void prem(int* nu…...

快问快答JS面向对象面试题
1、说说你对闭包的理解 使用闭包主要是为了设计私有的方法和变量。闭包的优点是可以避免全局变量的污染,缺点是闭包会常驻内存,会增大内存使用量,使用不当很容易造成内存泄露。在js中,函数即闭包,只有函数才会产生作用…...

googlenet论文理解
参考文章:https://www.cnblogs.com/czy4869/p/8977788.html 以及下面这篇的前几行让我弄懂了论文里说的稀疏性和计算性能兼顾:参考文章:https://blog.csdn.net/weixin_52121118/article/details/119740279...
OnnxRuntime TensorRT OpenCV::DNN性能对比(YoloV8)实测
1. 前言 之前把ORT的一套推理环境框架搭好了,在项目中也运行得非常愉快,实现了cpu/gpu,fp32/fp16的推理运算,同onnx通用模型在不同推理框架下的性能差异对比贴一下,记录一下自己对各种推理框架的学习状况 YoloV8模型大小 模型名称参数量NANO3.2M...... 2. CPU篇 CPU推理框架性…...

【QT 网络云盘客户端】——获取用户文件列表信息
目录 1.获取用户文件列表信息分析 2.设置图标属性 3.向服务器获取文件的数量 4.向服务器获取文件信息列表 4.显示图标 1.获取用户文件列表信息分析 1.将QListWidget设置为图标模式 2. 当我们点击"按下载量升序","按下载量降序",“更新” 菜单选项 都会…...

从0到1,无代码开发如何简化产品创新流程
在当今竞争激烈的市场环境中,产品创新已经成为企业成功的关键因素之一。为了在市场上保持竞争力,企业需要不断地推出新产品或改进现有产品。然而,传统的开发流程往往耗时费力,且成本高昂。因此,简化产品创新流程成为了…...
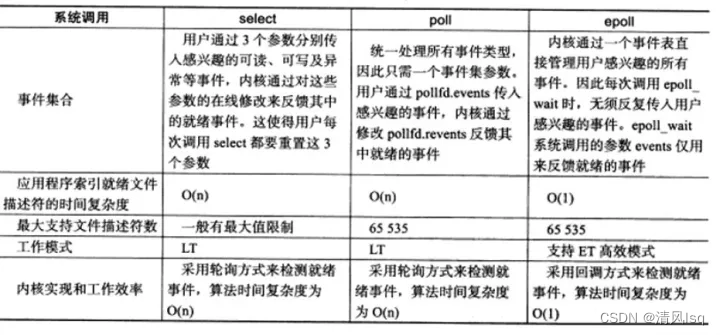
select、epoll 的快速核心理解
一、 select 最low的就是在用户代码中自旋实现所有阻塞socket的监听。但是每次判断socket是否产生数据,都涉及到用户态到内核态的切换。 于是select改进:将fd_set传入内核态,由内核判断是否有数据返回; 然后最low的只能使用自旋…...

HTTP和HTTPS的区别
一、两者概念 1.1 HTTP概念 HTTP 的全称是超文本传输协议(HyperText Transfer Protocol) 是一种用于分布式、协作式和超媒体信息系统的应用协议,简单来说就是一种分布和接收HTML页面的方法,被用于在Web浏览器和网站服务器之间传递…...
)
分布式异步任务处理组件(二)
一些关键点的设计脑暴记录----very important!!! 首先,任务存储交给kafka,由节点负责写入kafka,acks1;失败重试;透传kafka的提交可靠性,保证任务提交成功;后…...
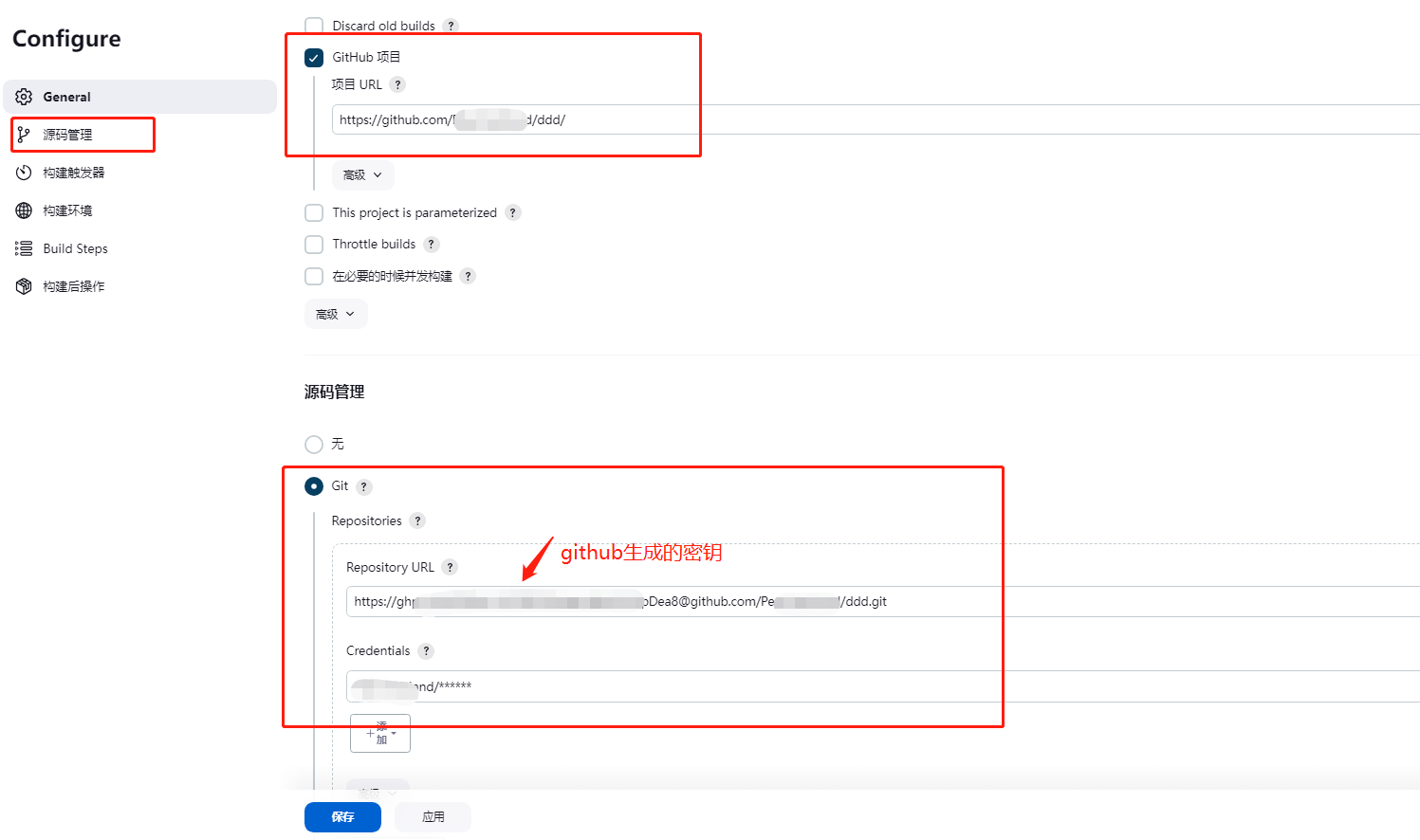
Jenkins 拉取 GitHub 私有仓库失败问题
添加仓库的时候提示 stderr: fatal: Cannot prompt because user interactivity has been disabled. 把在 GitHub账户设置中生成的个人访问令牌填到地址里...

小程序 多层次对象数组的赋值、动态赋值
1、给对象赋值 data: {form: {Name: ,IDCard: ,Sex: ,}},对单个属性赋值 this.setData({form.Name:章三,[form.Sex]:女,}) 动态赋值 onChangeDate(e) {let field e.currentTarget.dataset.field;this.setData({[form.${field}]: e.detail.data})}, field 是wxml上通过dat…...

angular踩坑
1 新版路由守卫由于canActivate已被废弃,采用函数函数,但其参数中无法像类一样进行路由对象注入,如何实现路由首位中的页面跳转? import { CanActivateFn,Router,ActivatedRouteSnapshot, RouterStateSnapshot,} from angular/ro…...
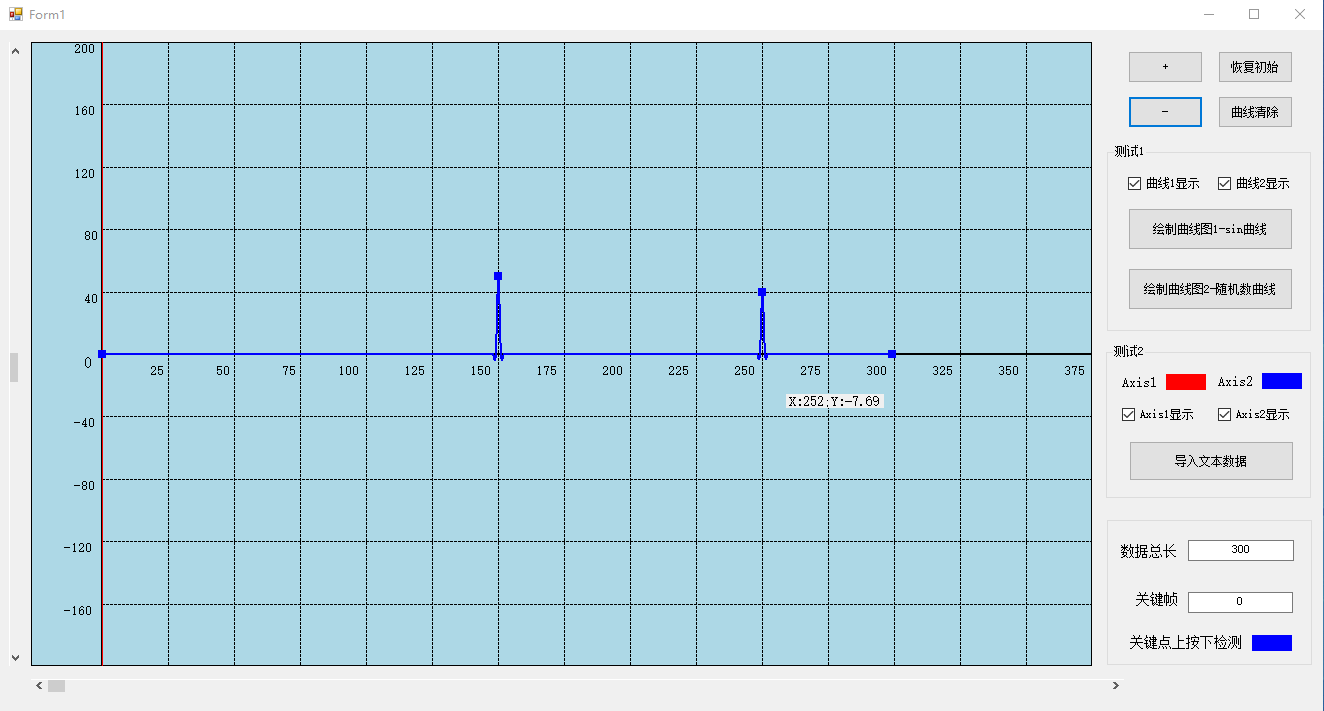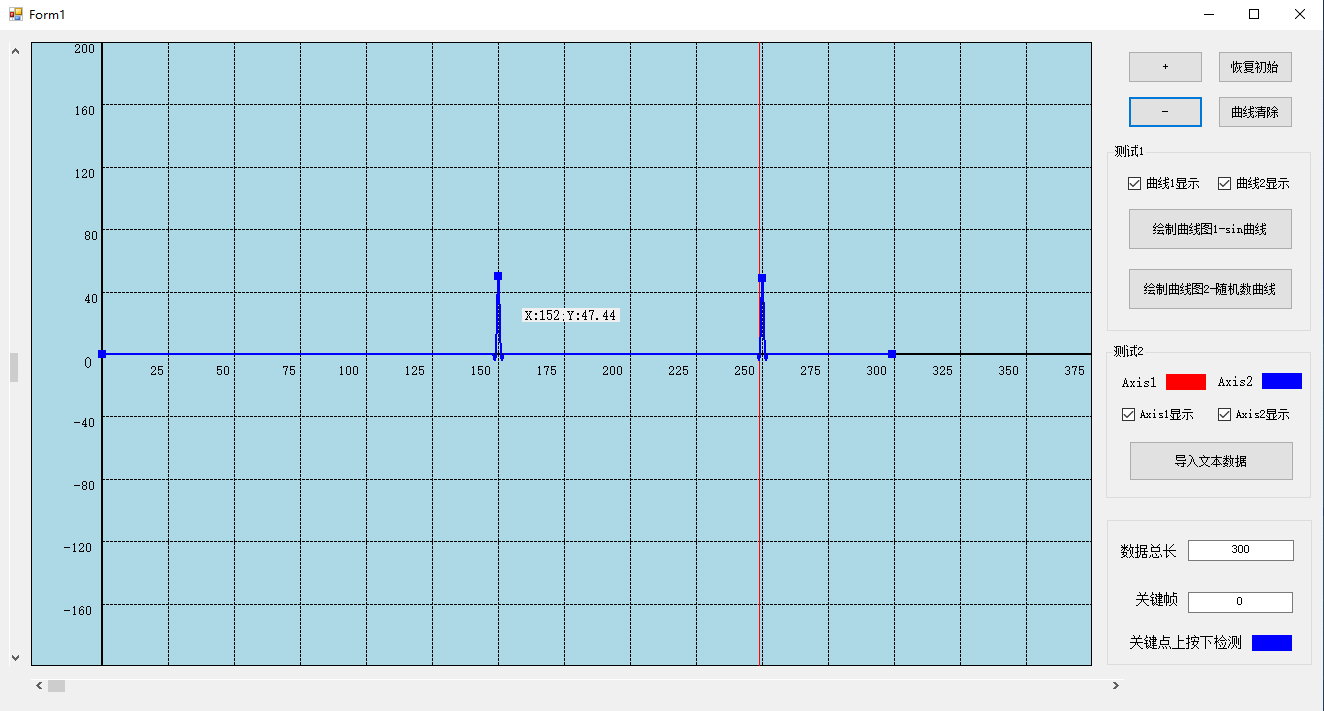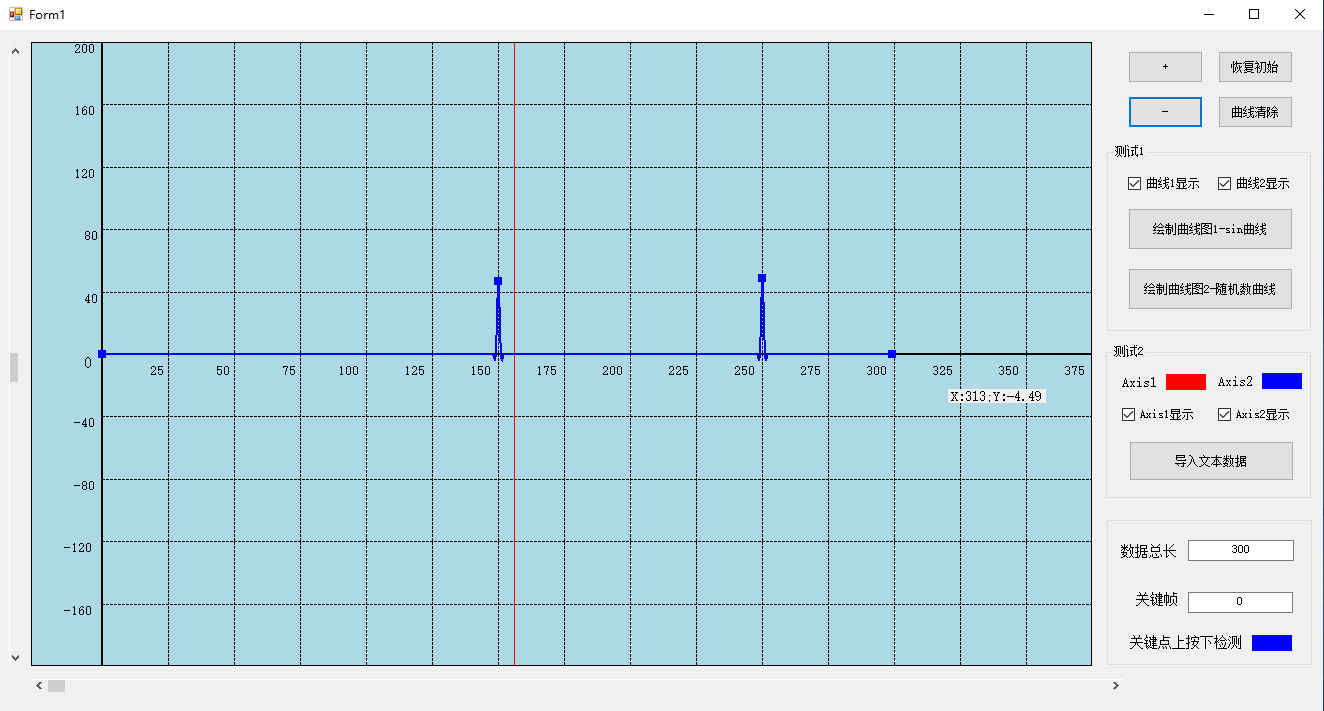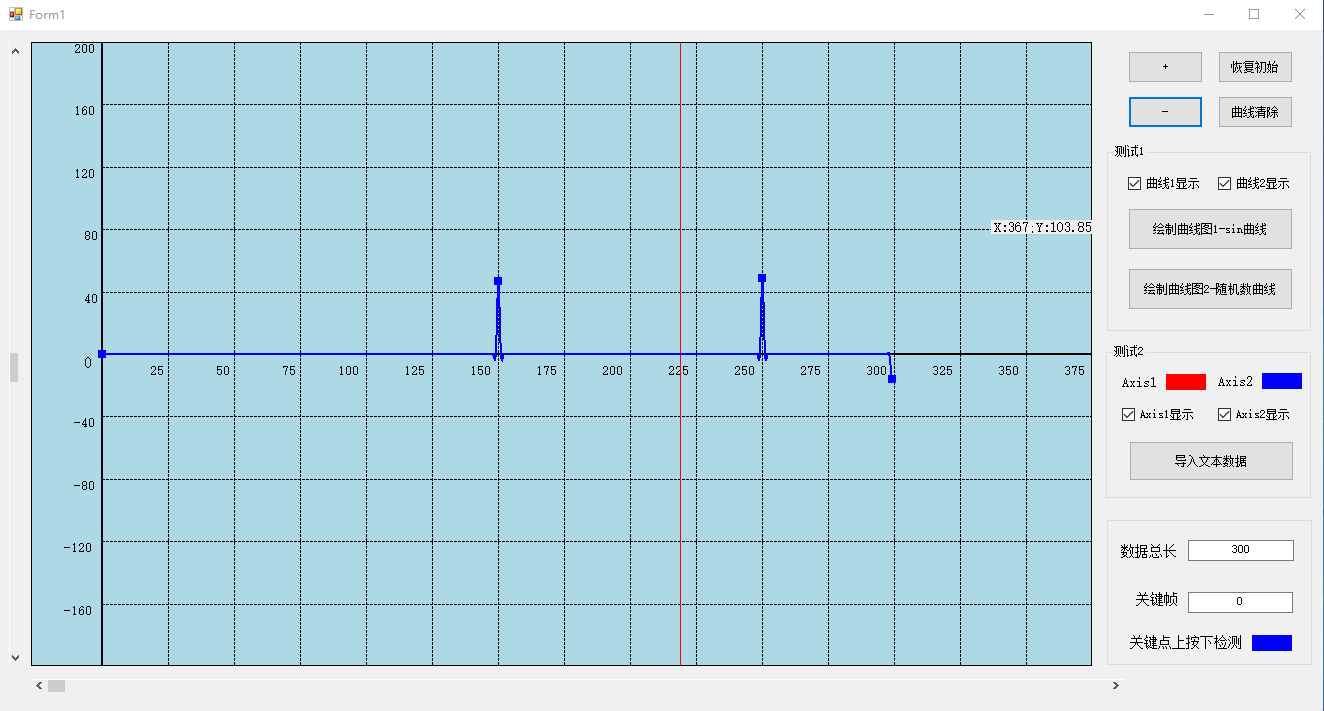
C#时间轴曲线图形编辑器开发1-基本功能
目录 一、前言 1、简介 2、开发过程 3、工程下载链接 二、基本功能实现 1、绘图面板创建 (1)界面布置 (2)显示面板代码 (3) 面板水平方向、竖直方向移动功能实现 (4)面板放…...
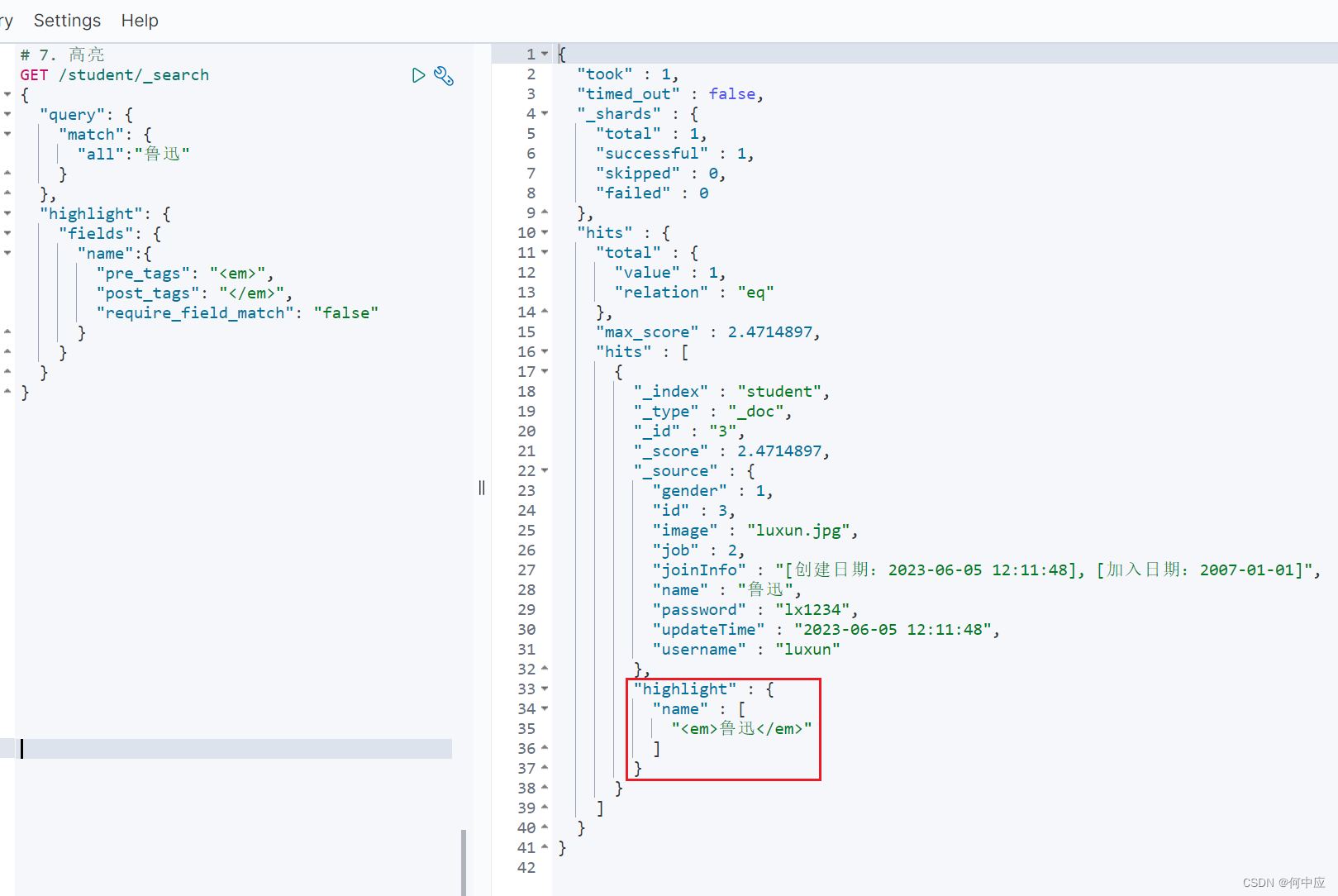
elasticsearch查询操作(DSL语句方式)
说明:本文介绍在kibana,es的可视化界面上对文档的查询操作; 添加数据 先使用API,创建索引库,并且把数据从MySQL中查出来,传到ES上,参考(http://t.csdn.cn/NaTHg) 索引库…...

JavaScript详解
目录 一、JavaScript是什么? 1.1、JavaScript 和 HTML 和 CSS 之间的关系 1.2、JavaScript 运行过程 1.3、JavaScript 的组成 二、JavaScript 的书写形式 1. 行内式 2. 内嵌式 3、外部式 注释 三、输入输出 输入: prompt 输出: alert 输出: …...
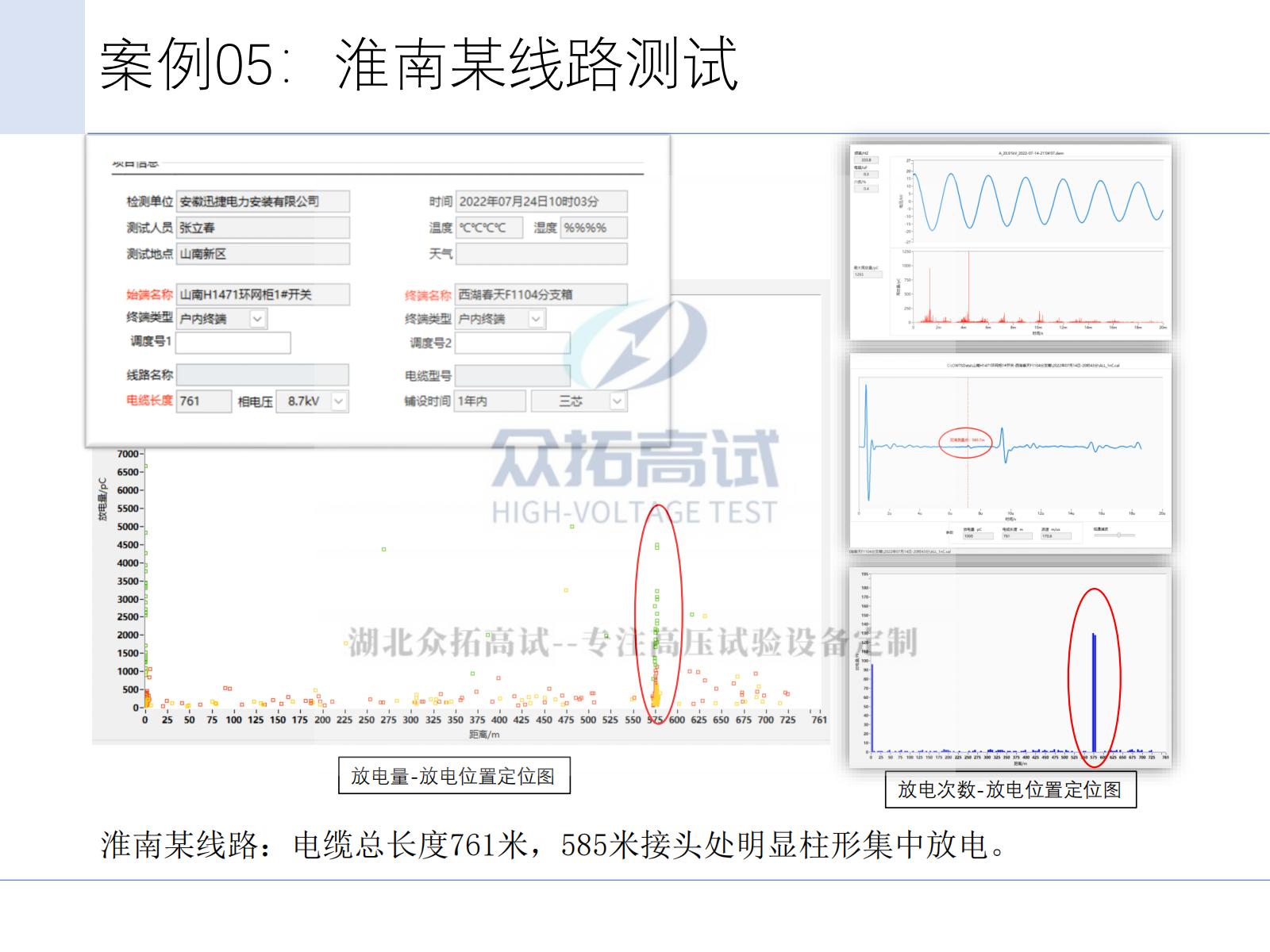
电缆振荡波局部放电检测定位技术
电缆振荡波检测技术主要用于交联聚乙烯电力电缆检测,是属于离线检测的一种有效形式 。该技术基于LCR阻尼振荡原理,在完成电缆直流充电的基础上,通过内置的高压电抗器、高压实时固态开关与试品电缆形成阻尼振荡电压波,在试品电缆上…...
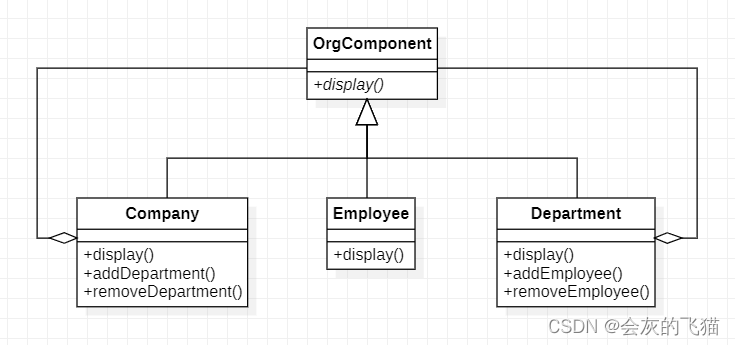
AI Chat 设计模式:10. 组合模式
本文是该系列的第八篇,采用问答式的方式展开,问题由我提出,答案由 Chat AI 作出,灰色背景的文字则主要是我的一些思考和补充。 问题列表 Q.1 给我介绍一下组合模式A.1Q.2 好的,给我举一个组合模式的例子,使…...
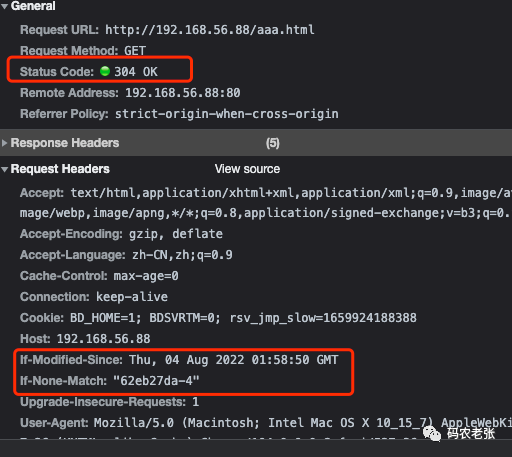
【Nginx12】Nginx学习:HTTP核心模块(九)浏览器缓存与try_files
Nginx学习:HTTP核心模块(九)浏览器缓存与try_files 浏览器缓存在 Nginx 的 HTTP 核心模块中其实只有两个简单的配置,这一块也是 HTTP 的基础知识。之前我们就一直在强调,学习 Nginx 需要的就是各种网络相关的基础知识&…...

【1】-Locust性能测试工具介绍与安装
Locust介绍 locust是一个开源的压测工具,其官网地址是Locust - A modern load testing framework,通过编写Python代码,可以轻松实现百万级的并发,相对于我们熟悉的Jmeter来说,其对压测机的要求更低,而且使…...
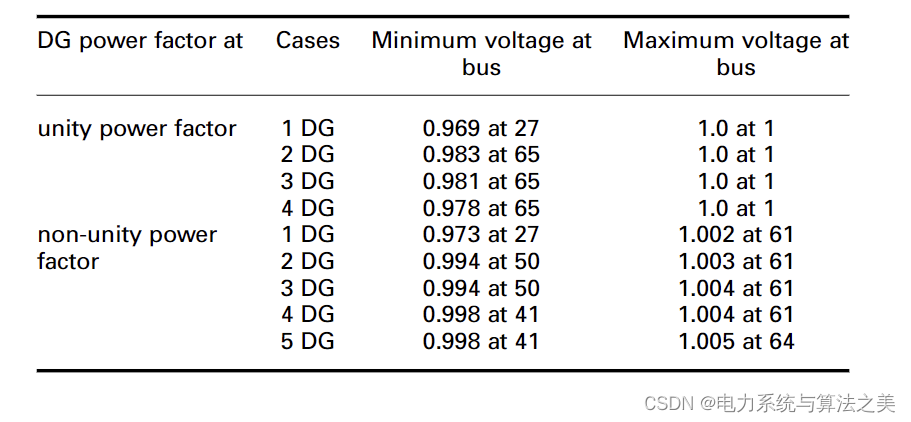
基于拉格朗日-遗传算法的最优分布式能源DG选址与定容(Matlab代码实现)
目录 1 概述 2 数学模型 2.1 问题表述 2.2 DG的最佳位置和容量(解析法) 2.3 使用 GA 进行最佳功率因数确定和 DG 分配 3 仿真结果与讨论 3.1 33 节点测试配电系统的仿真 3.2 69 节点测试配电系统仿真 4 结论 1 概述 为了使系统网损达到最低值&a…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
