树及其遍历
文章目录
- 树
- 树定义
- 专业术语
- 树分类
- 二叉树
- 分类
- 存储
- 连续存储(完全二叉树)
- 链式存储
- 一般树的存储
- 森林的存储
- 线索二叉树
- 哈夫曼树
- 构造步骤
- 遍历
- 先序遍历
- 中序遍历
- 后续遍历
- 链式二叉树遍历具体代码
- 已知两种遍历序列求原始二叉树
- 已知先序和中序求后序
- 已知中序和后序求先序
- 已知先序和后序求中序
- 树的应用
树
树定义
像这种有层次关系进行存储的,就是一棵树,是非线性结构。
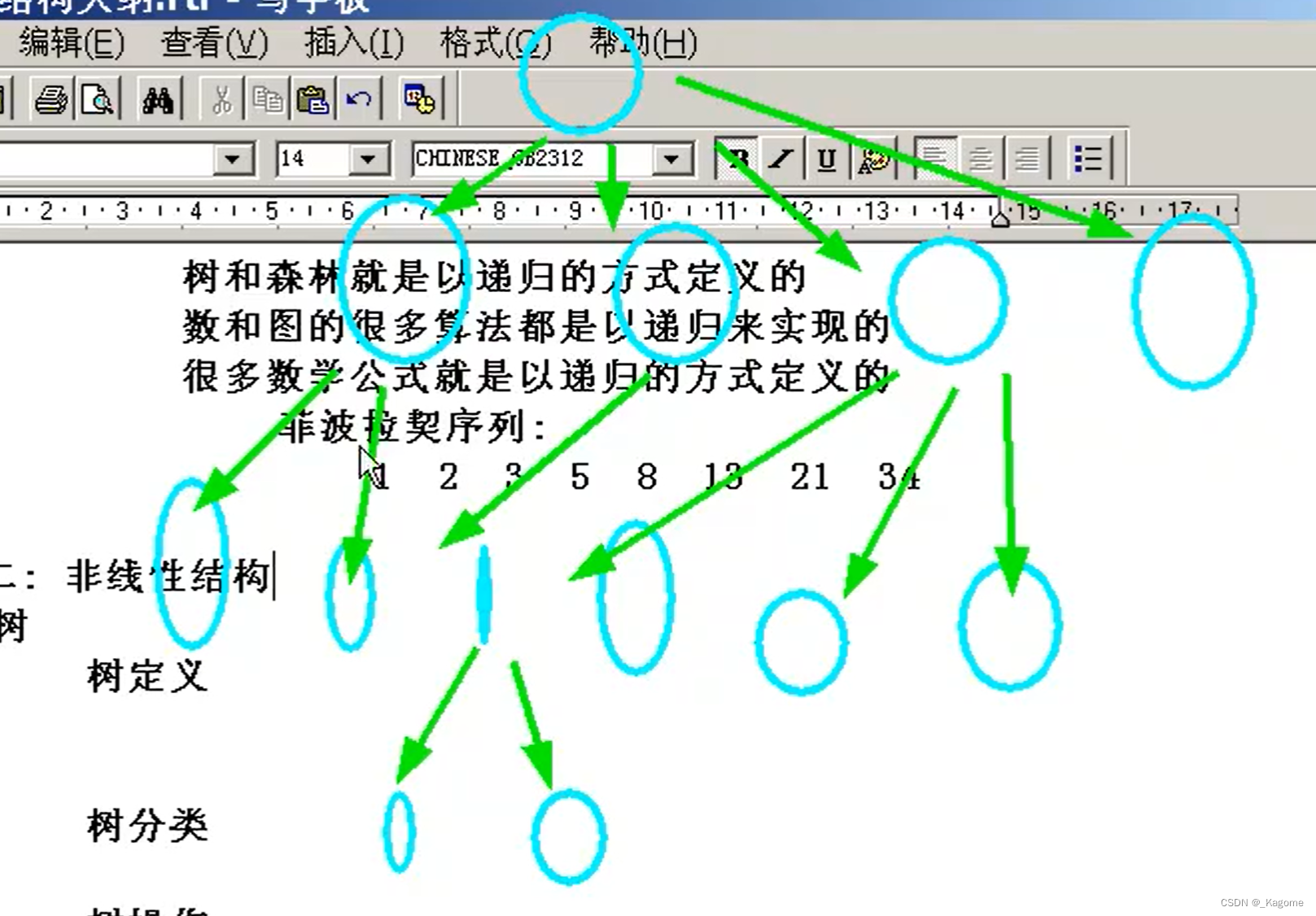
以递归的方式进行定义。
专业定义:
- 有且只有一个称为根的节点。
- 有若干个互不相交的子树,这些子树本身也是一棵树。
通俗定义:
- 树是由节点和边组成。
- 每一个节点节点只有一个父节点但可以有多个子节点。
- 有一个节点例外,该节点没有父节点,此节点称为根节点。
专业术语
- 节点:就是一个个的圈。
- 父节点:和当前节点上一个紧挨着的节点。
- 子节点:父节点下连着的子节点。
- 子孙:父节点下的所有节点。
- 深度:从根节点到最底层的层数称为深度。
- 叶子节点:没有子节点的节点。
- 非终端节点:实际上就是非叶子节点,有子节点的节点。
- 根节点:看有没有子节点。
- 度:子节点的个数称为度。
树分类
- 一般树:任意一个节点的子节点的个数都不受限制
- 二叉树:任意一个节点的子节点个数最多两个,且子节点的位置不可更改。
- 森林:有互不相交的,一般的树合在一起,就是森林。
二叉树
分类
- 一般二叉树
- 满二叉树:在不增加树的层数的前提下,无法再多添加一个节点的二叉树就是满二叉树。
- 完全二叉树:如果只是删除了满二叉树最底层最右边的连续若干个节点,这样形成的二叉树就是完全的二叉树。
满二叉树是完全二叉树的一个特例。
存储
连续存储(完全二叉树)
要把一颗一般的二叉树以数组方式存储的话,必须先把这个一般的二叉树转化为完全二叉树。
eg:
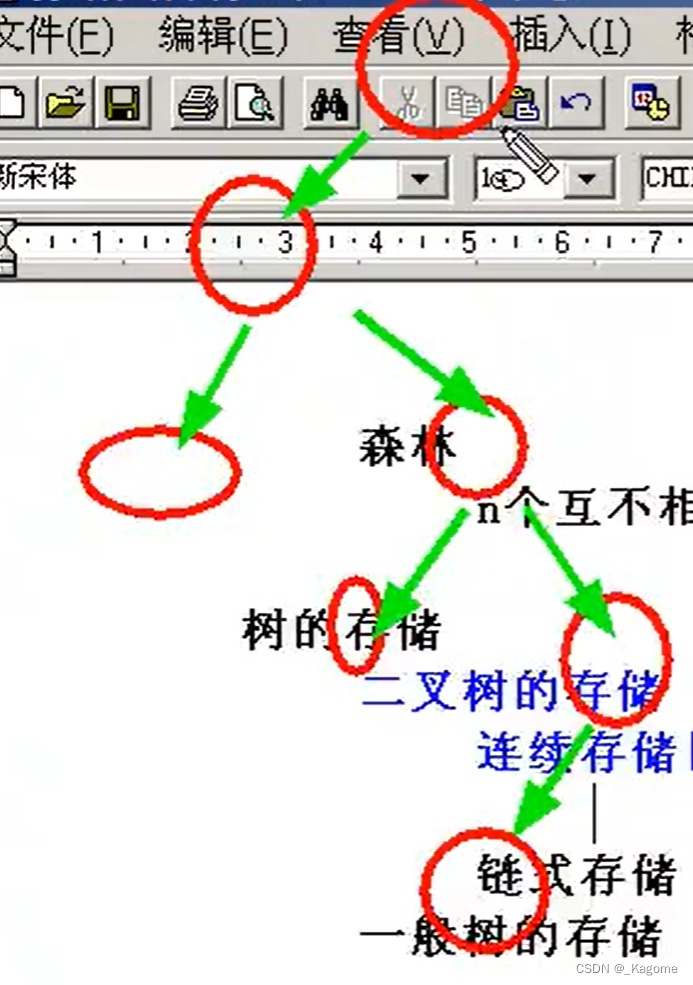
首先这不是一个完全二叉树,因为完全二叉树先是一个满的二叉树,后来再在最底一层砍。所以要使用连续存储就必须先把这个二叉树变成完全二叉树。
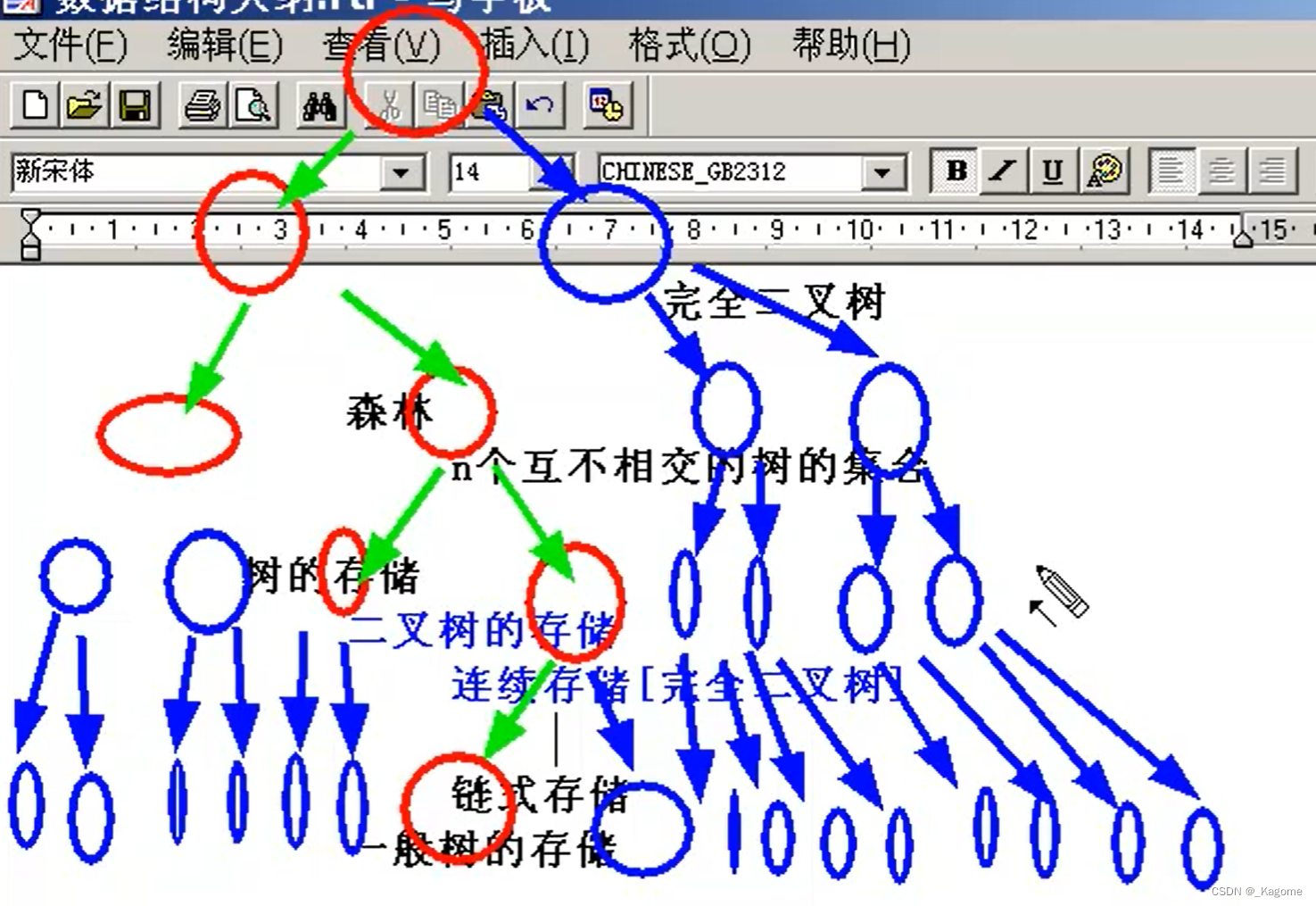
先变成满二叉树,再把最底层的最右边得到删掉,就成了完全二叉树。
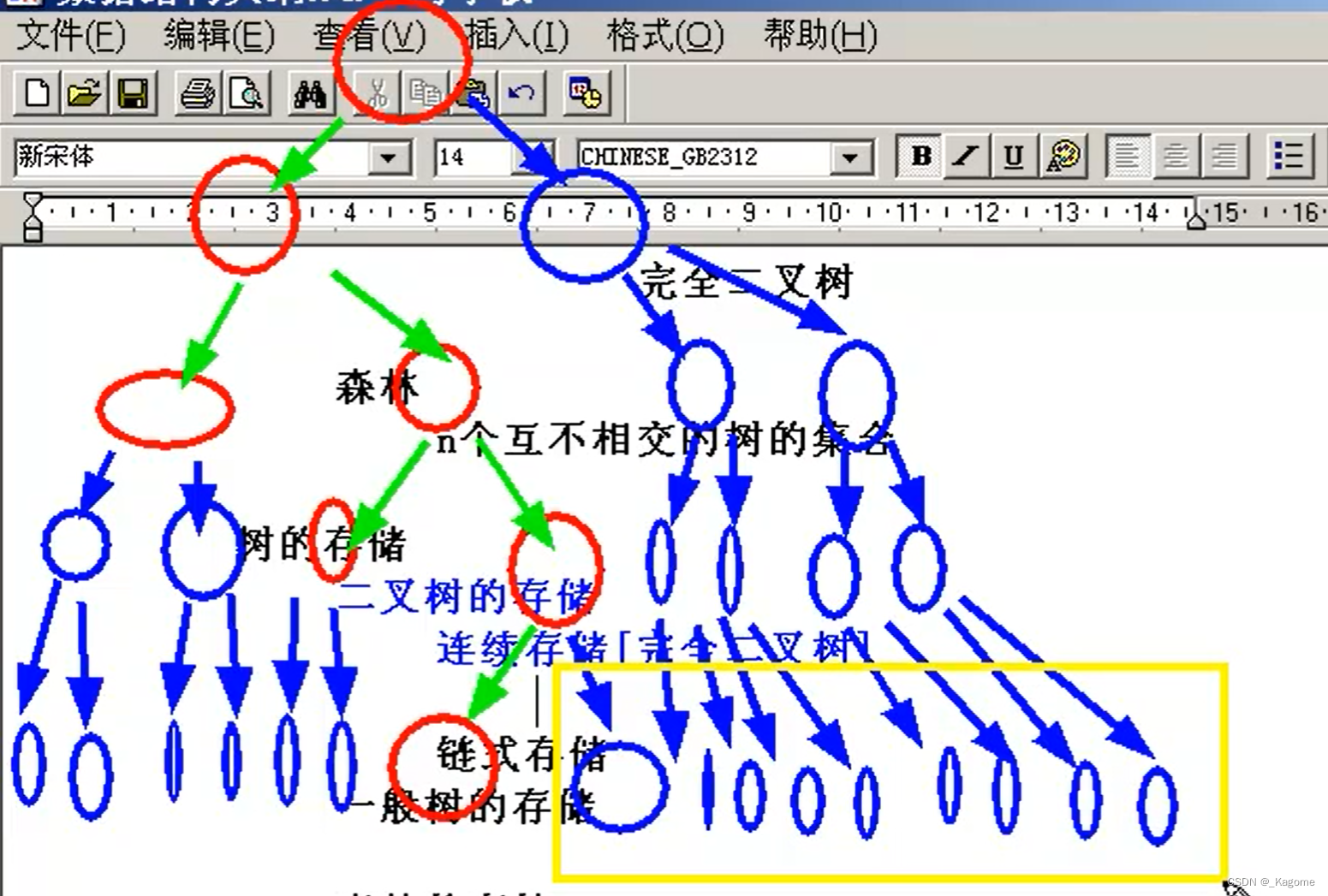
黄色线框的可以不保存。(先转化成满二叉树,再把最后一层最右边开始的点删掉,就是完全二叉树)红色的是有效节点,别人是无法通过零散的红色有效节点还原二叉树的本来面目的。(排序通过先中后进行排序。)
树是非线性的,将非线性的数转换成线性结构的,结果是不知道的。
数组只能以完全二叉树的方式进行存储,即不能只存放有效节点,因为通过先中后进行排序后,还原不了其本来的面目。所以把所有点都存进去,才好还原。
优点:查找某个节点的父节点和子节点很快。
缺点:耗用内存空间过大。
链式存储
通过指针域弄成一个连续的存储。
一般树的存储
- 双亲表示法:求父节点很方便,因为跟的是下标。
- 孩子表示法:求子节点方便,跟着的是子节点。
- 双亲孩子表示法:有链表,有数组,有下标,指针域,求父节点与子节点都很方便,就是代码复杂。
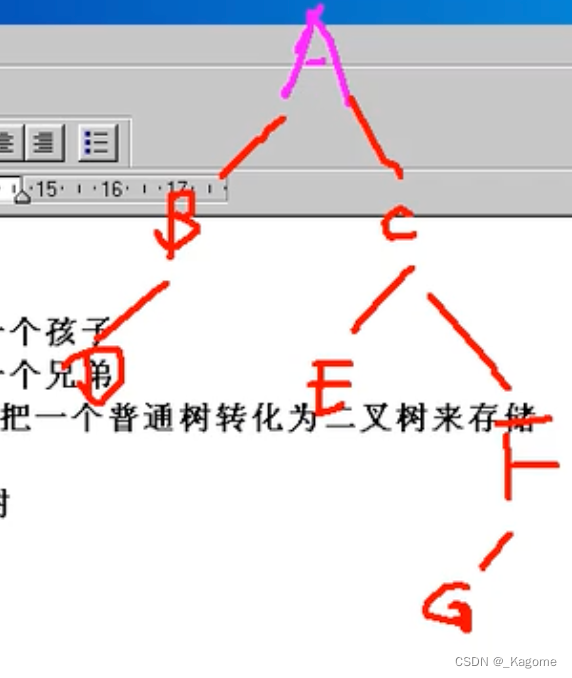
- 二叉树表示法:把一个普通树转化成二叉树来存储,具体转换方法是,设法保证任意一个节点左指针域指向它的第一个孩子,右指针域指向它的下一个兄弟节点,只要能满足此条件,就能把一个普通的数转化为二叉树。(转化时,只有左边的孩子,右边都是与孩子并列的兄弟,即一个普通的数转化为二叉树就没有右子树。例如下方的2,3,4,5,真正是孩子的只有2,然后3,4,5都是与其并列的项,排在右边。3也没有左兄弟,所以把4排在右边,5就同理了。)
eg如下,将一个普通的树转化为二叉树。
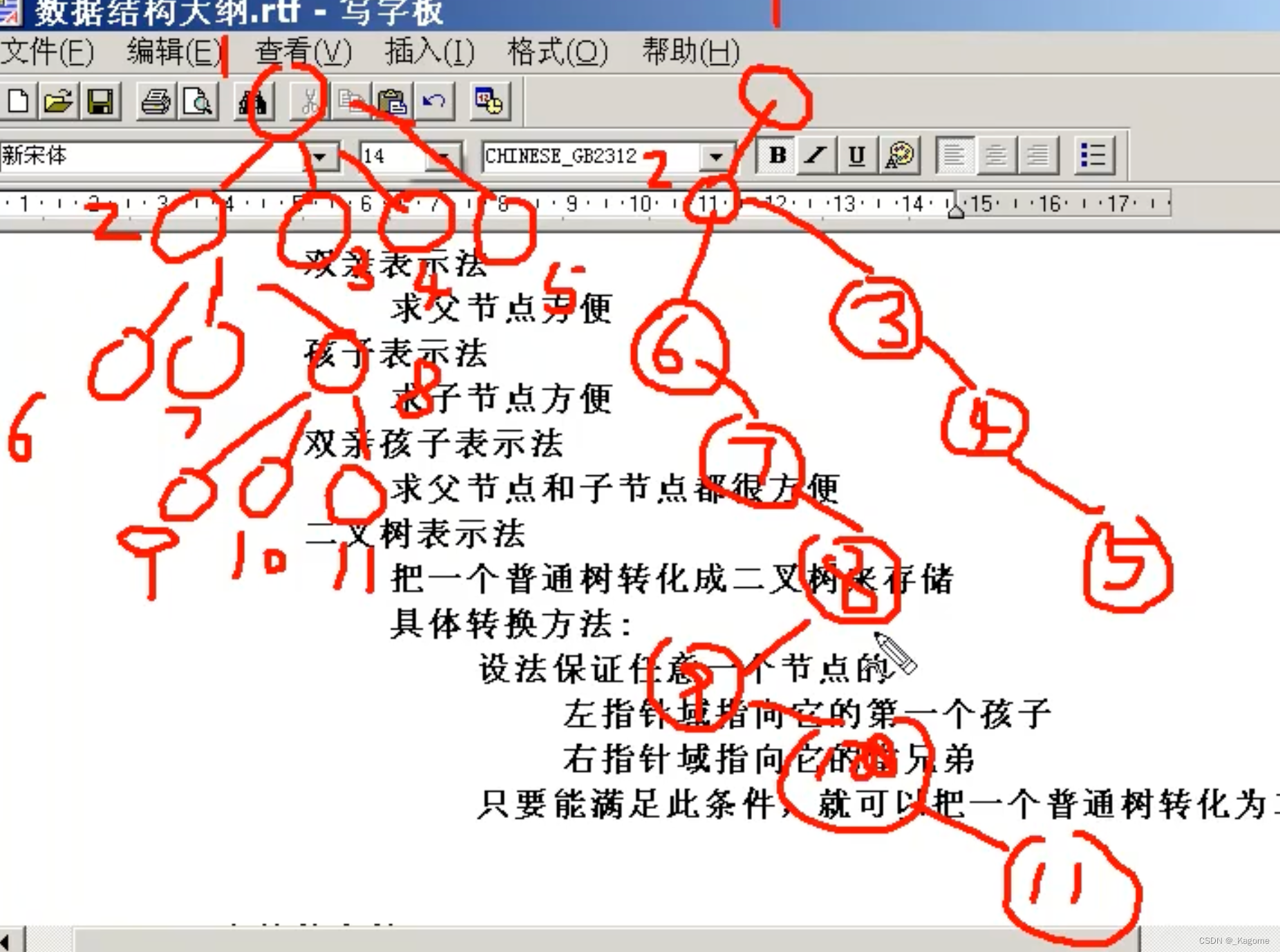
森林的存储
几个树互不相交,就组成了一个森林。
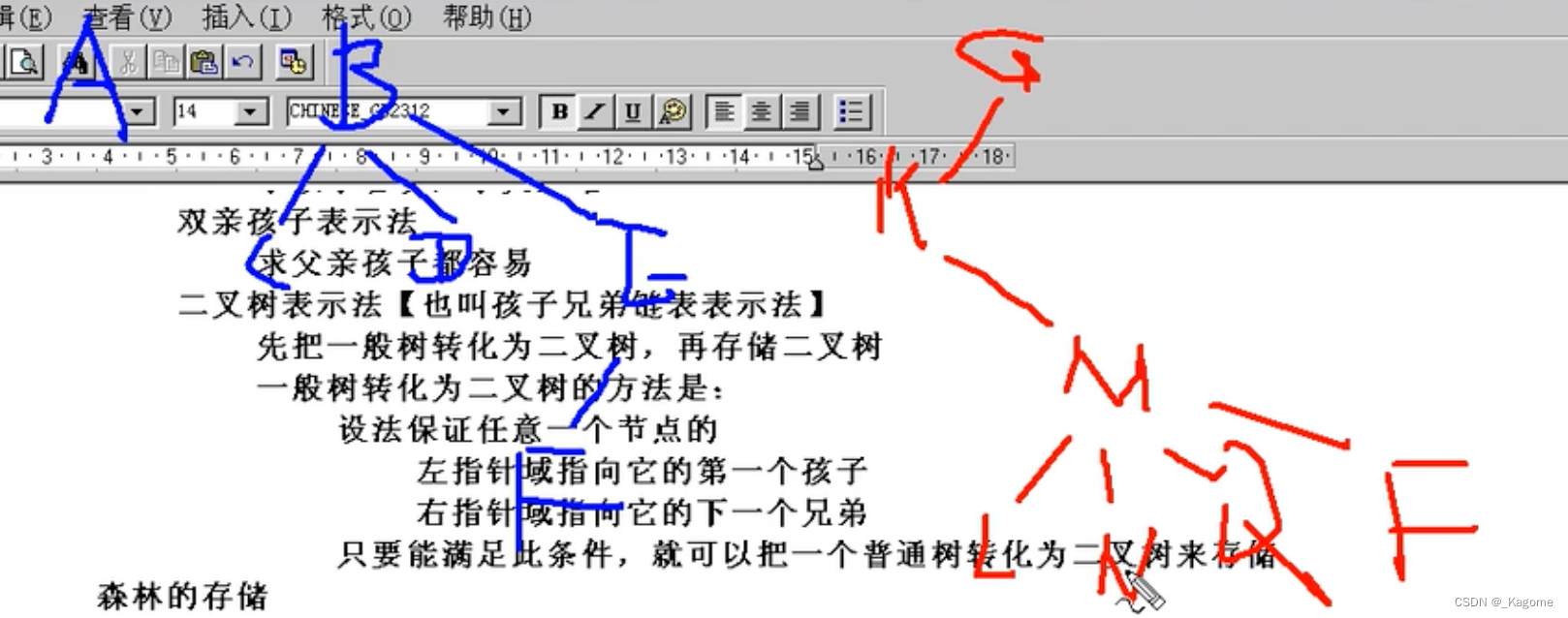
先把森林转化为一个二叉树,再进行存储。而森林的二叉树存储规则为:把B当A的兄弟,把G当B的兄弟。
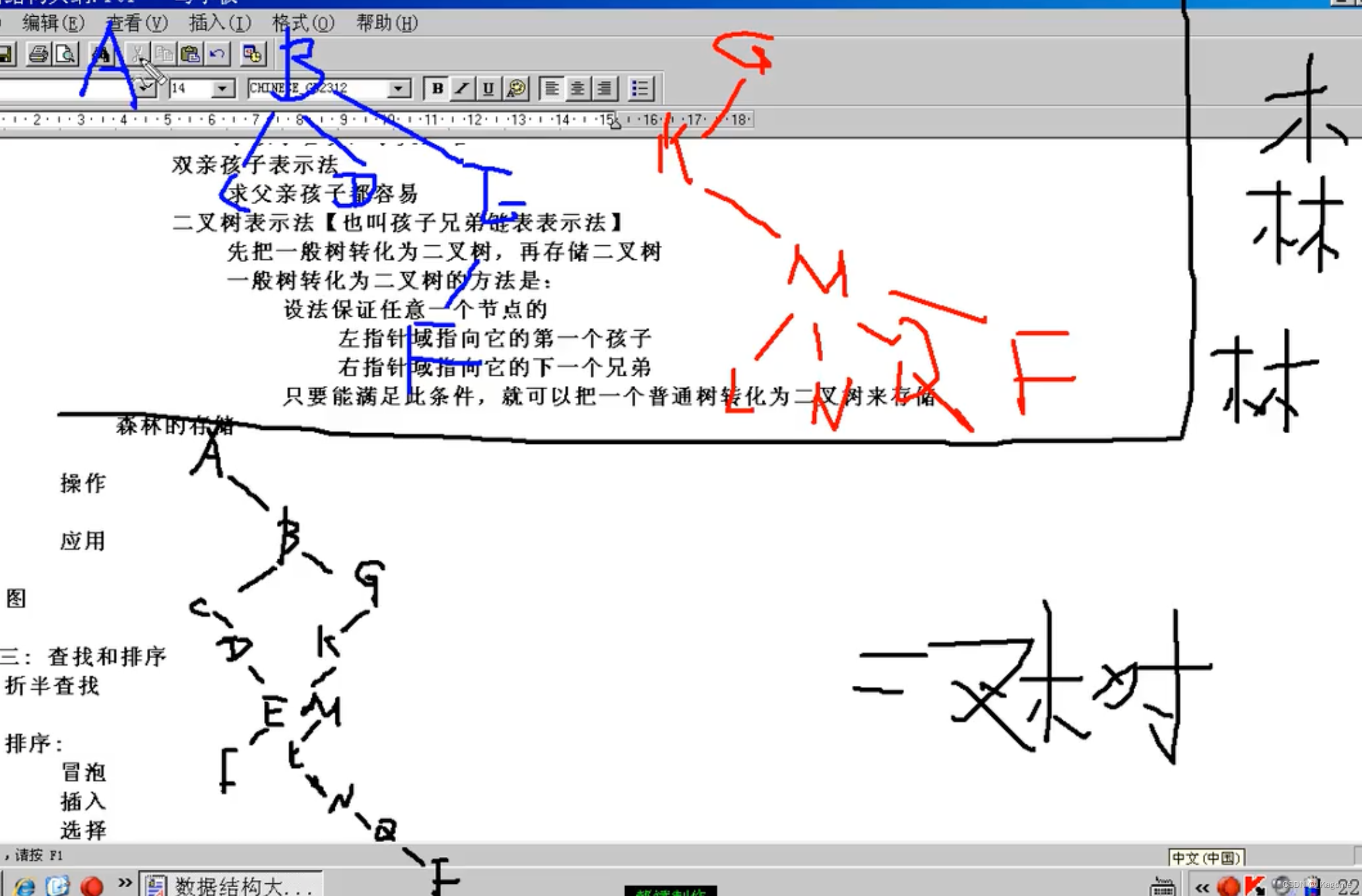
森林转成二叉树的步骤与之前一般树转化为二叉树也是一致的。
线索二叉树
当用二叉链表作为二叉树的存储结构时,可以很方便地找到某个结点的左右孩子;但一般情况下,无法直接找到该结点在某种遍历序列中的前驱和后继结点。

因为还剩下了n+1个指针域,将其利用起来,存储前驱后继指针的地址,称此为线索。
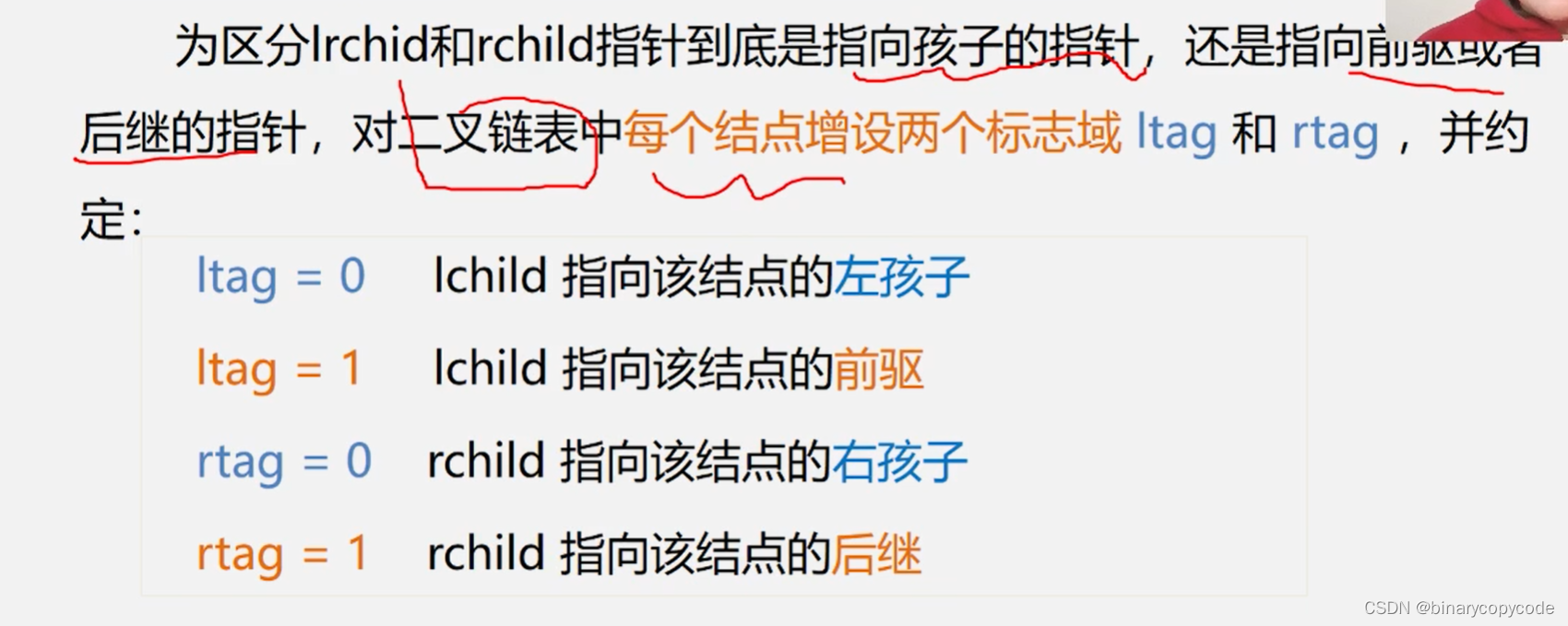
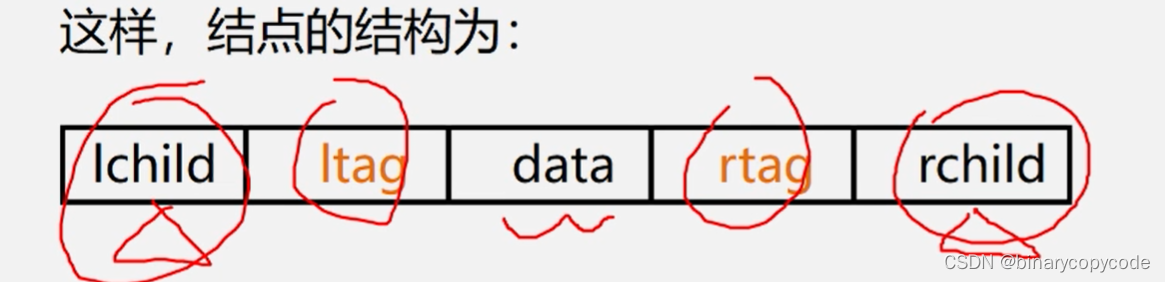
可以用ltag与rtag的方式来区分是否为孩子还是线索。(左孩子与前驱,右孩子与后继)
//线索二叉树的结点结构
typedef struct BiThrNode{int data;int ltag, rtag;struct BiThrNode *lchild, rchild;
}BiThrNode, *BiThrTree;
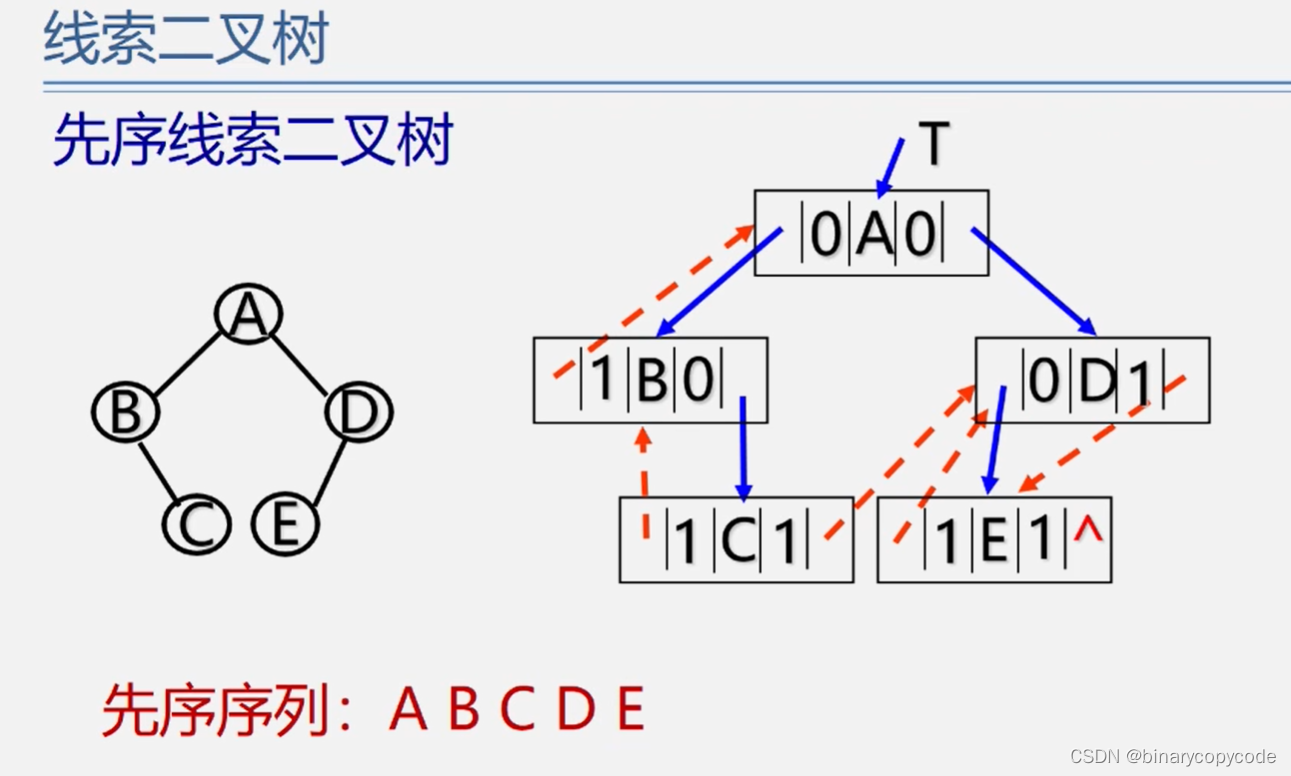
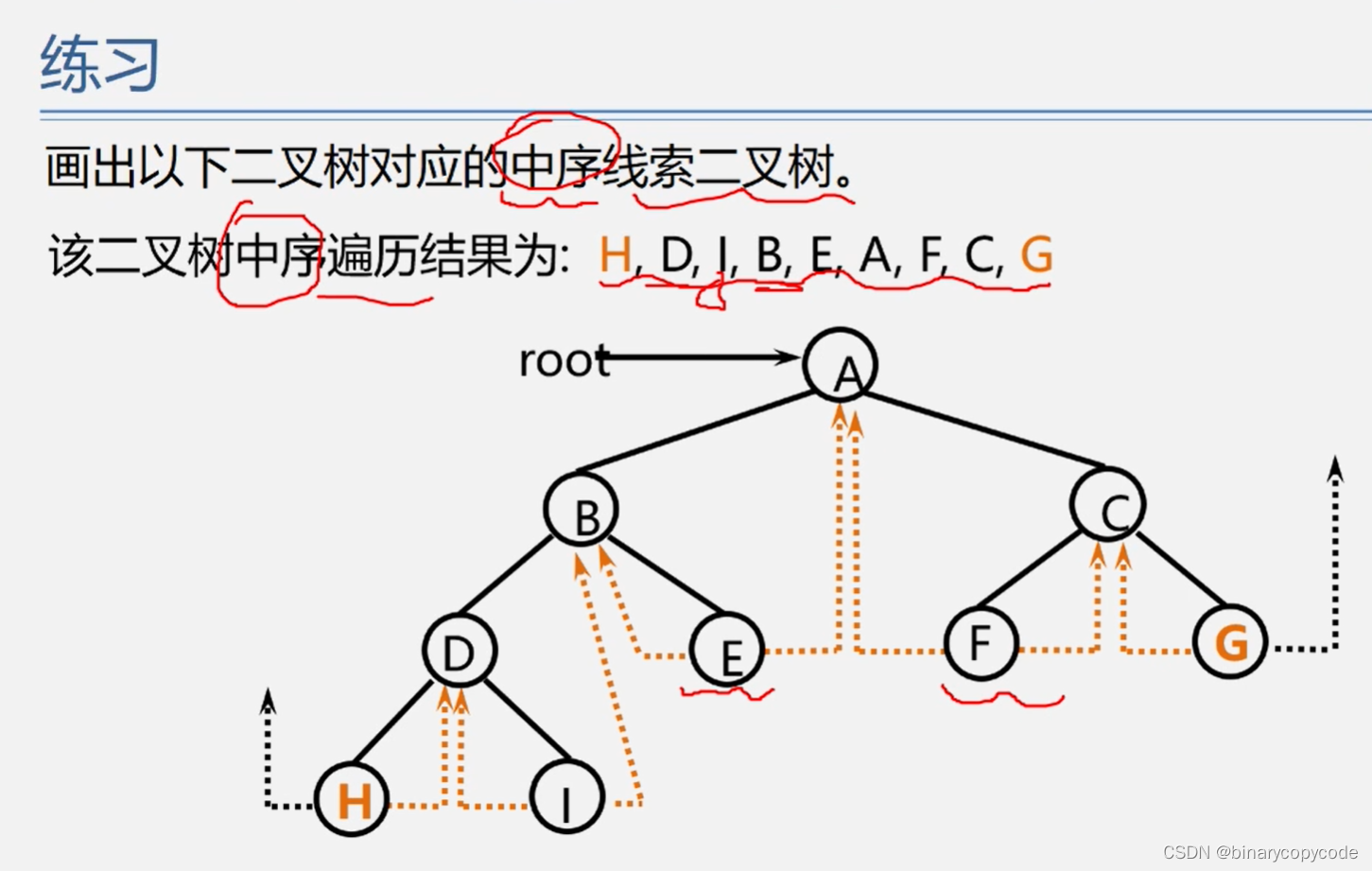
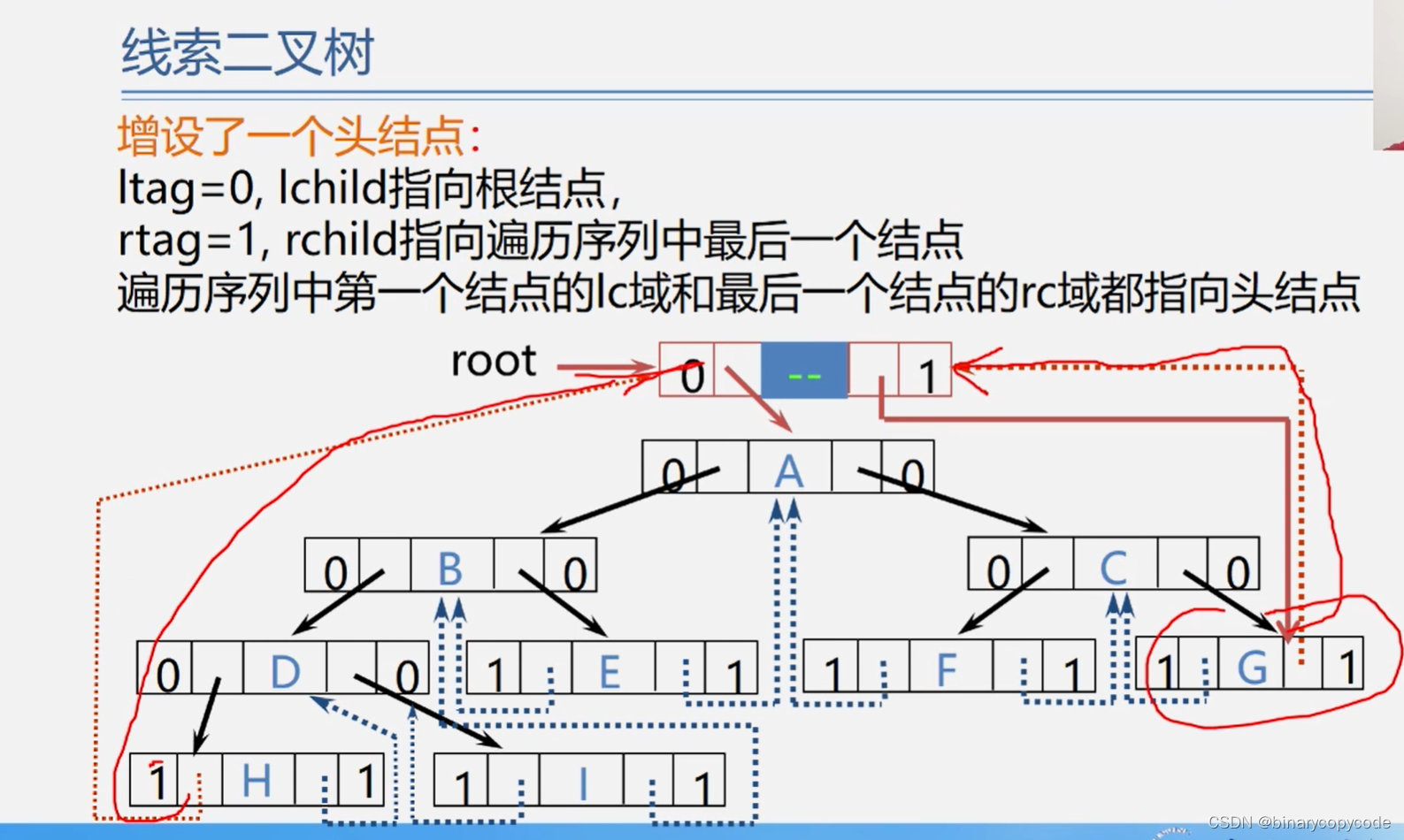
因为首尾还有两个指针域悬空,可以增加一个头结点,让其指向头结点。
哈夫曼树
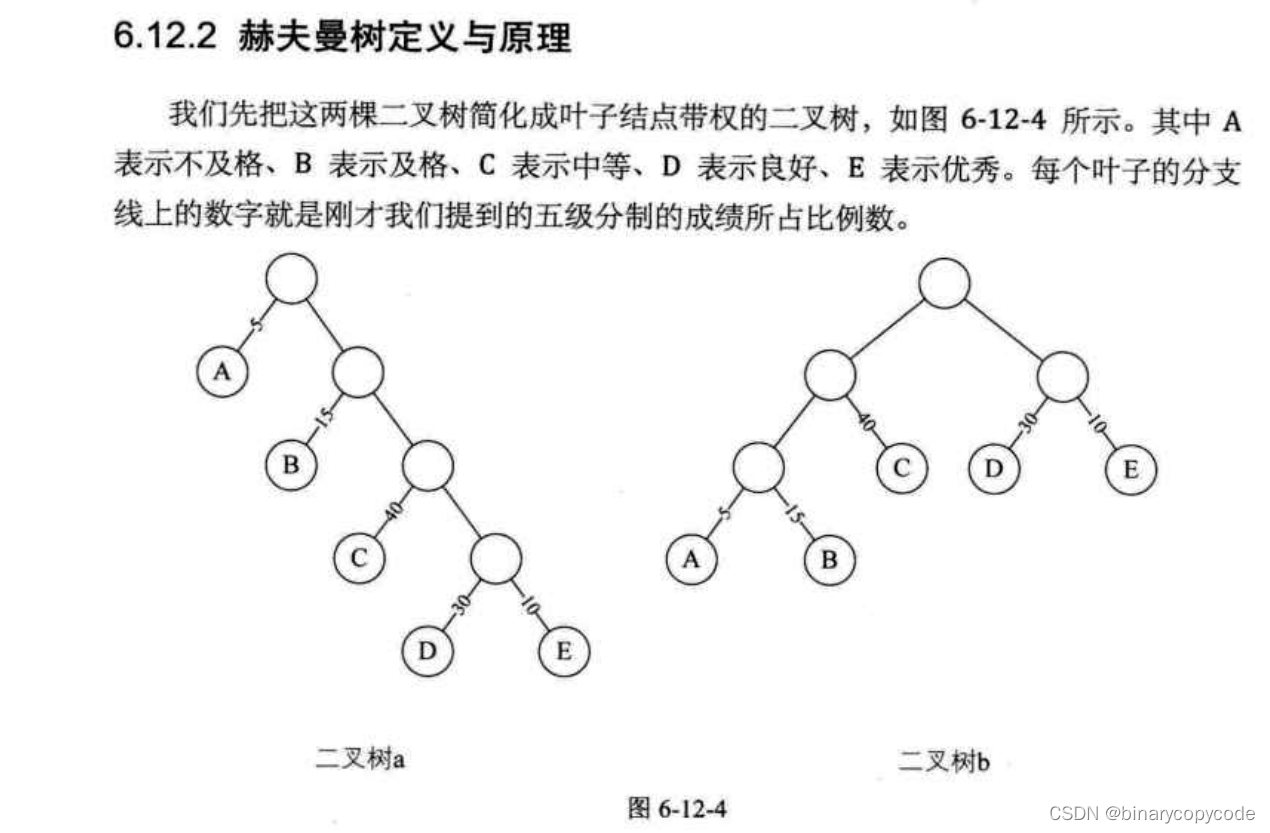
相当于把一个带权重的树进行重排,排成一个考虑权重最优的二叉树。
构造步骤
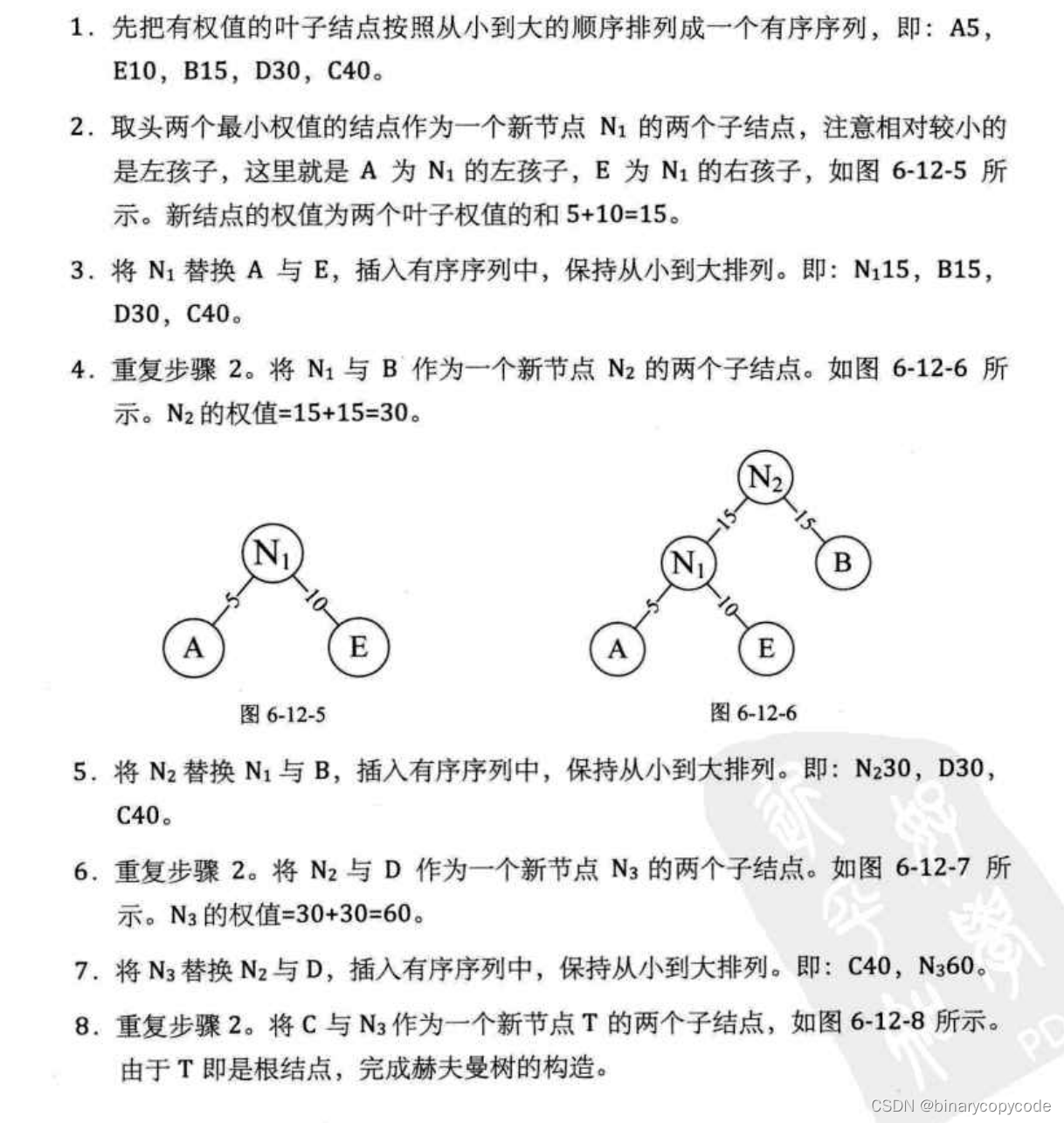
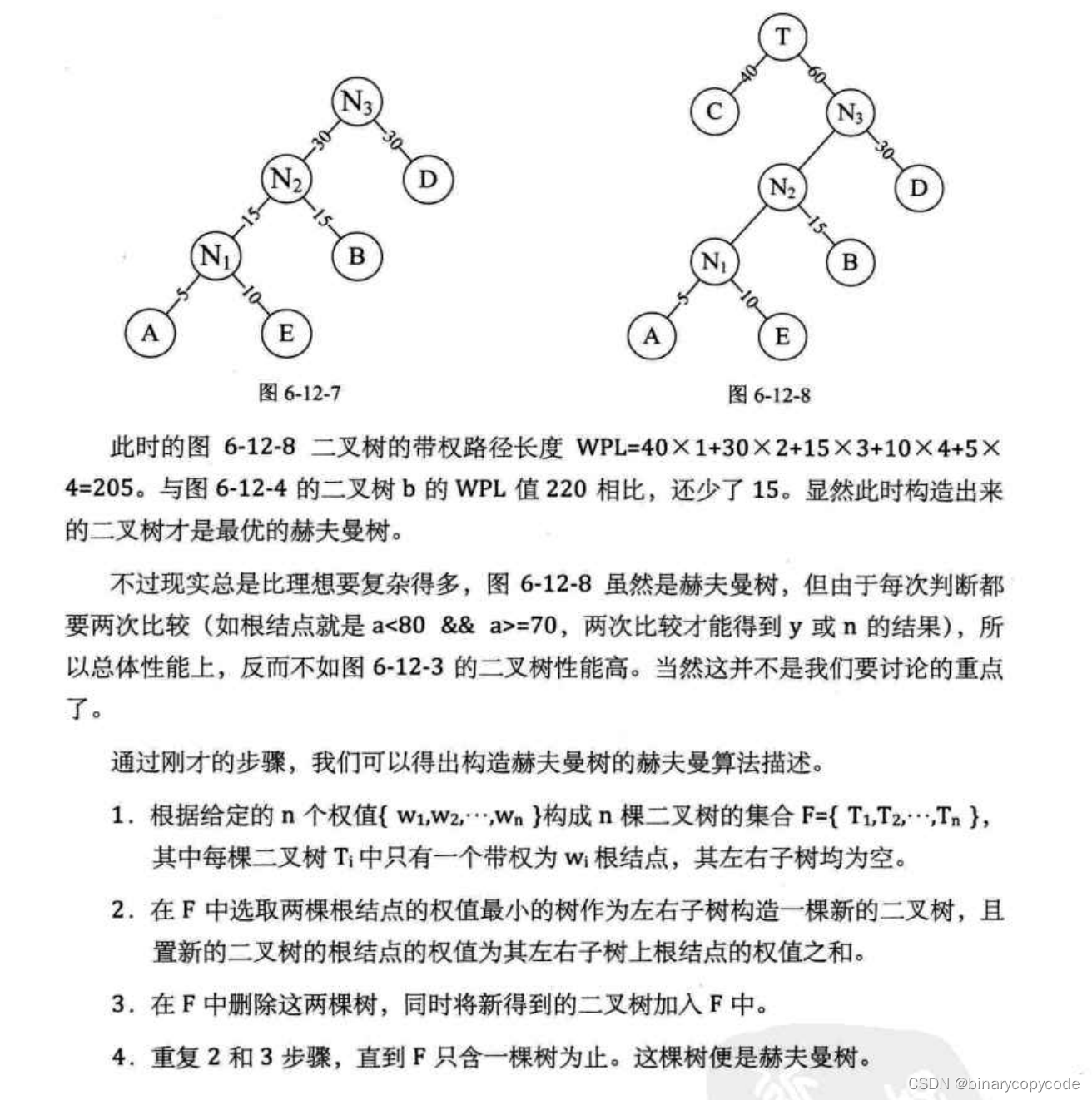
两个权重相同的直接连接,权重不相同的按照权重小的为左孩子,权重大的为右孩子的原则,进行排列。
遍历
把非线性的树转化成非线性的序列。
先序遍历
先访问根节点,再先序访问左子树,再先序访问右子树。假设二叉树如下:
运用递归的思想,先访问根节点A,再先序访问左子树,再先序访问右子树。在访问左子树的时候,因为左子树也是一棵树,所以会又绕到了先访问根节点B,再顺着来看左子树与右子树,即B的左子树为D,B没有右子树,因为D没有左子树以及右子树,为空,则此次递归结束,BD访问完毕;紧接着先序遍历A的右子树,右子树是个二叉树,再从根节点开始,再遍历左子树,再遍历右子树。都访问完毕之后,才是访问完毕。
eg:
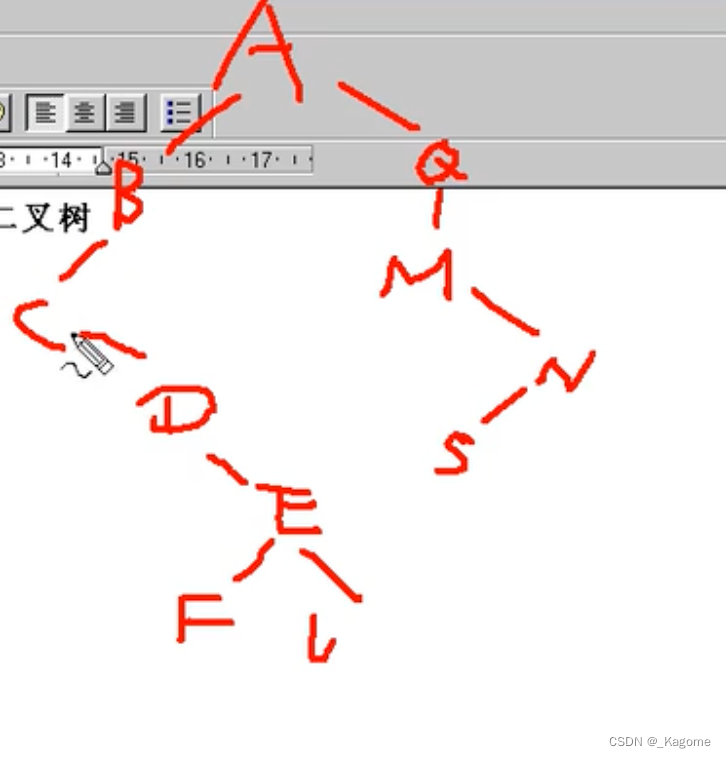
最后的遍历节点就是ABCDEFLQMNS。
中序遍历
中序遍历左子树,再访问根节点,再中序遍历右子树。
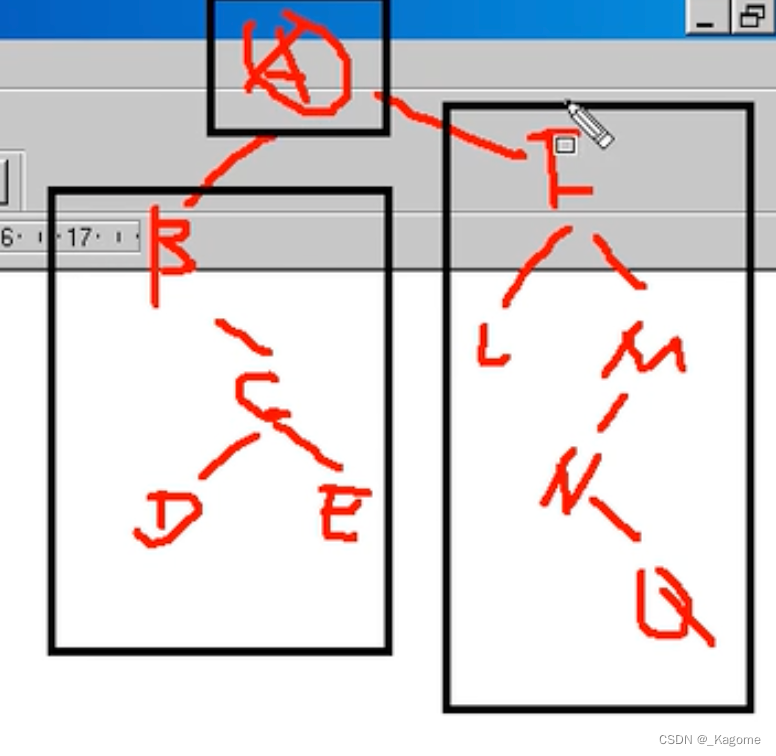
先中序遍历左子树,B的左子树为空,所以先访问左子树的根节点,即为B,所以先B,B访问完访问B的右子树,也是非空的,所以递归思想,B的右子树先去中序遍历左子树,B的左子树为C的左子树,所以先访问D,再访问根节点C,再访问E。
最后顺序为BDCEALFNQM
eg:
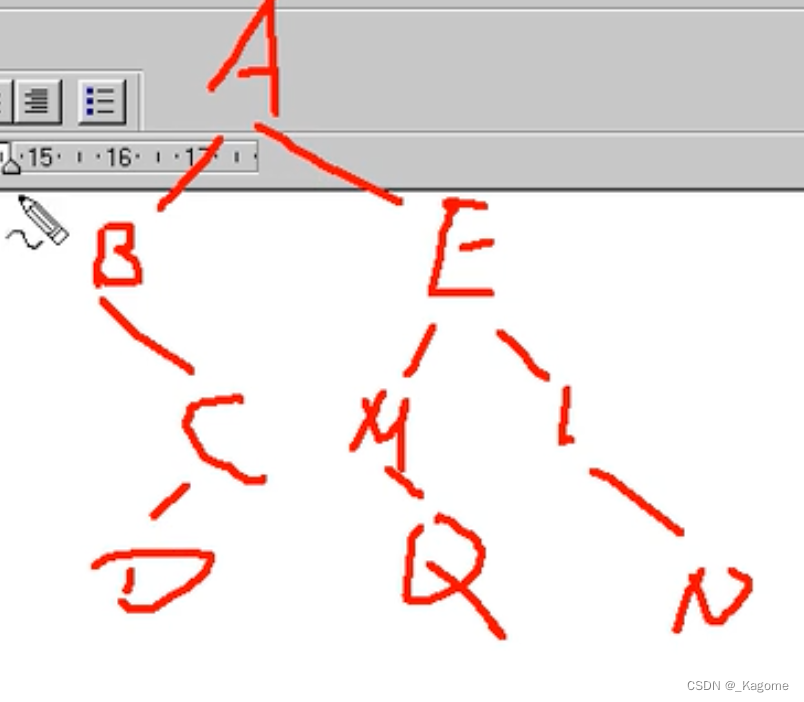
遍历顺序:BDCAMQELN
后续遍历
中序遍历左子树,中序遍历右子树,再访问根节点。遍历都是以根节点的顺序来判断的。
eg:
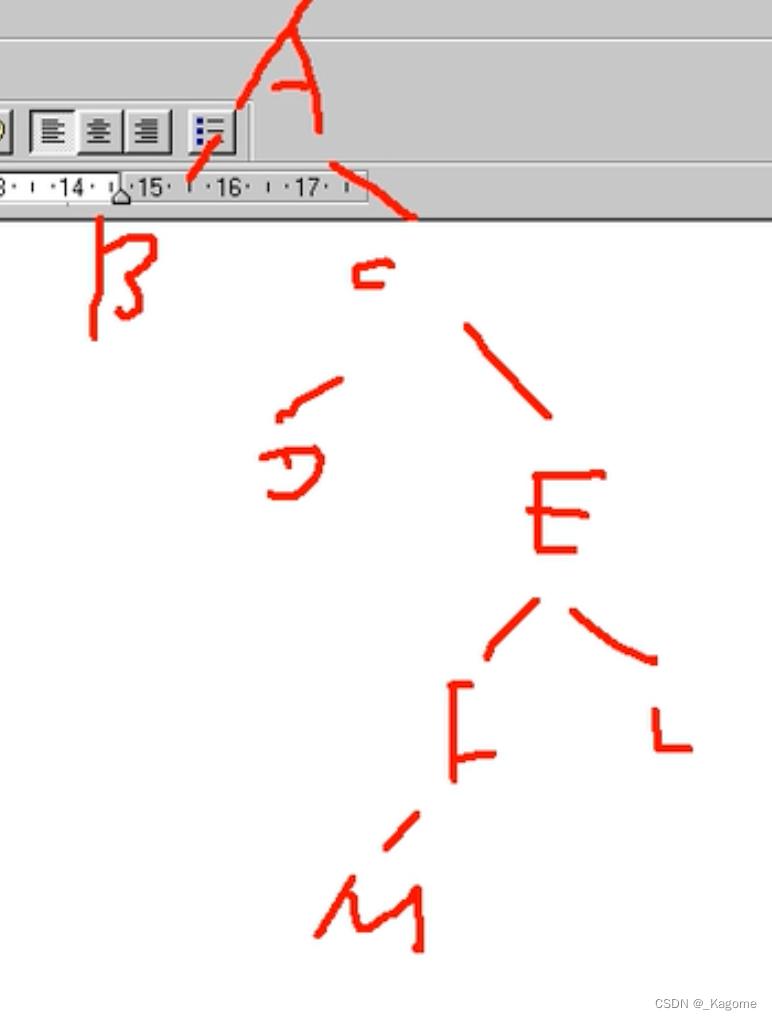
遍历顺序:BDMFLECA(先全部的左,再全部的右,最后根)
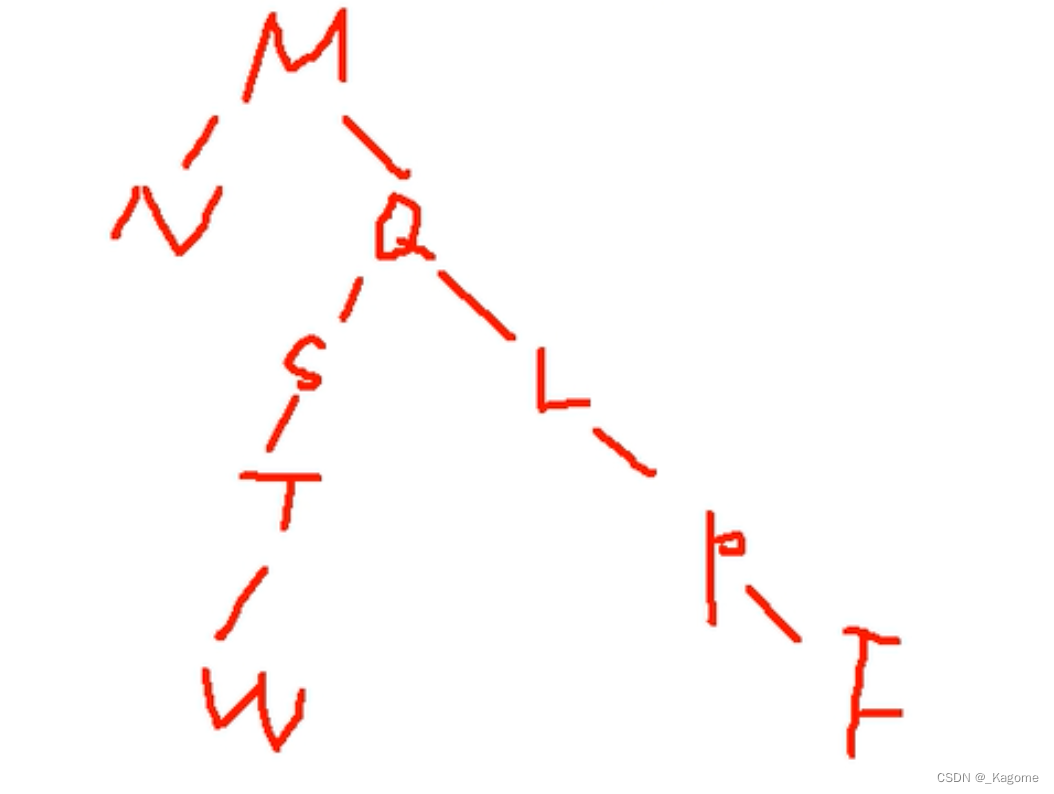
遍历顺序:NWTSFPLQM
链式二叉树遍历具体代码
# include <stdio.h>
# include <malloc.h>struct BTNode
{char data;struct BTNode * pLchild; struct BTNode * pRchild;
};void PostTraverseBTree(struct BTNode * pT);
struct BTNode * CreateBTree(void);
void PreTraverseBTree(struct BTNode * pT);
void InTraverseBTree(struct BTNode * pT);int main(void)
{struct BTNode * pT = CreateBTree();// PreTraverseBTree(pT);
// InTraverseBTree(pT);PostTraverseBTree(pT);return 0;
}void PostTraverseBTree(struct BTNode * pT)
{if (NULL != pT){if (NULL != pT->pLchild){PostTraverseBTree(pT->pLchild);} if (NULL != pT->pRchild){PostTraverseBTree(pT->pRchild);}printf("%c\n", pT->data);}
}void InTraverseBTree(struct BTNode * pT)
{if (NULL != pT){if (NULL != pT->pLchild){InTraverseBTree(pT->pLchild);}printf("%c\n", pT->data);if (NULL != pT->pRchild){InTraverseBTree(pT->pRchild);} }
}void PreTraverseBTree(struct BTNode * pT)
{if (NULL != pT){printf("%c\n", pT->data);if (NULL != pT->pLchild){PreTraverseBTree(pT->pLchild);}if (NULL != pT->pRchild){PreTraverseBTree(pT->pRchild);} }
}struct BTNode * CreateBTree(void)
{struct BTNode * pA = (struct BTNode *)malloc(sizeof(struct BTNode));struct BTNode * pB = (struct BTNode *)malloc(sizeof(struct BTNode));struct BTNode * pC = (struct BTNode *)malloc(sizeof(struct BTNode));struct BTNode * pD = (struct BTNode *)malloc(sizeof(struct BTNode));struct BTNode * pE = (struct BTNode *)malloc(sizeof(struct BTNode));pA->data = 'A';pB->data = 'B';pC->data = 'C';pD->data = 'D';pE->data = 'E';pA->pLchild = pB;pA->pRchild = pC;pB->pLchild = pB->pRchild = NULL;pC->pLchild = pD;pC->pRchild = NULL;pD->pLchild = NULL;pD->pRchild = pE;pE->pLchild = pE->pRchild = NULL;return pA;
}
已知两种遍历序列求原始二叉树
单纯的知道先中后三种序列当中的任何一个,都不能把原始的二叉树序列还原回来,当已知两种序列,可以推出原始的二叉树。
已知先序和中序求后序
示例1:
先序:ABCDEFGH
中序:BDCEAFHG
求后序:因为根据先序,第一个访问的一定是根节点,所以根节点为A,再中序,中间的A确定是根节点,A旁边的是左子树,A右边的是右子树。确定了左子树BDCE与右子树FHG,现在分别找左右子树的根节点,由先序序列可知,先出现的肯定为根。之后确定根节点为BF,之后确定下一个根节点为C,因为中序先遍历左子树,所以D是C的左子树,E就是C的右子树,至此,A的左子树全部推完。右子树类似,推完F,发现在中序序列当中F左边没有点了,说明F没有左子树,只有右子树G,G的左边有H,所以H是G的左子树。
所以后序序列就是DECBHGFA
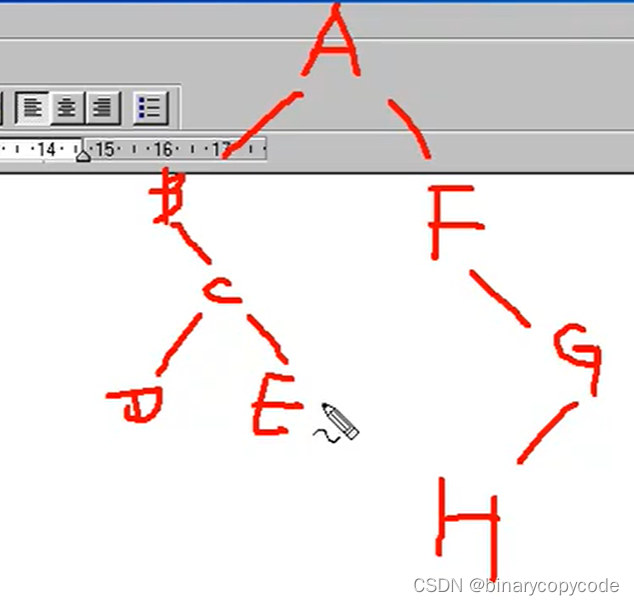
示例2:
先序:ABDGHCEFI
中序:GDHBAECIF
求后序:根节点为A,A的左子树为GDHB,右子树为ECIF,左子树当中,第一个根节点为B,B的左子树为GDH,D又为根节点,所以GH为其两树,G为左子树,H为右子树,至此A的左子树完全推出;A的右子树为ECIF,在ECIF当中,C为根节点,C的左子树为E,C的右子树为F,F的左子树为I,至此,A的右子树完全推出。
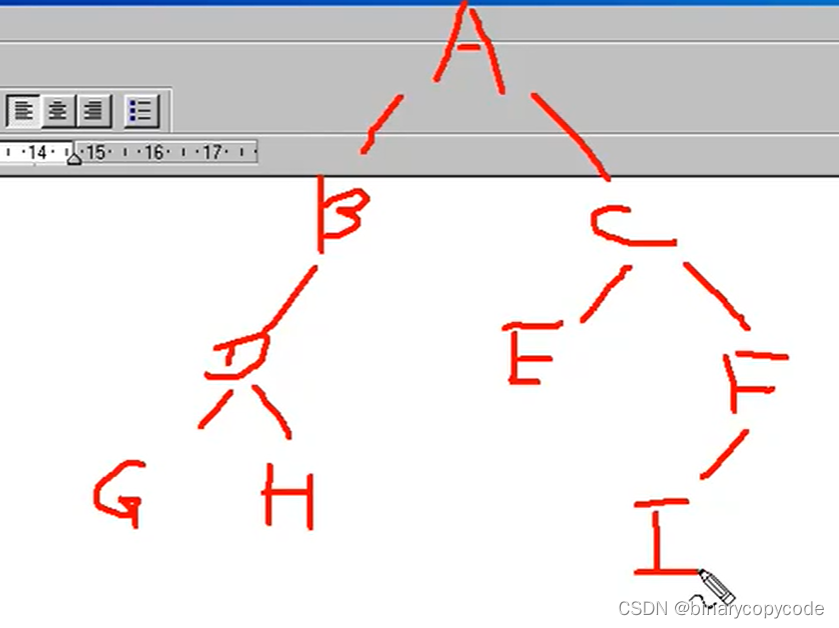
后序即为:GHDBIEFCA
已知中序和后序求先序
中序:BDCEAFHG
后序:DECBHGFA
求先序:根节点为A,最后出现的后序节点是根节点。所以BDCE是左子树,FHG是右子树。F是根节点,B也是根节点,因为在各个组合中最后出现(依照后序)再在中序中查找,B没有左子树,只有右子树DCE,C在后序最后出现,是根(哪一个在后序最后出现,哪一个就是根),所以C又有左子树又有右子树,左子树为D,右子树为E,至此A的左子树全部推完;A的右子树是FHG,F是根节点,F只有右子树HG,根节点为G,G有左子树H,至此,A的右子树全部推完。
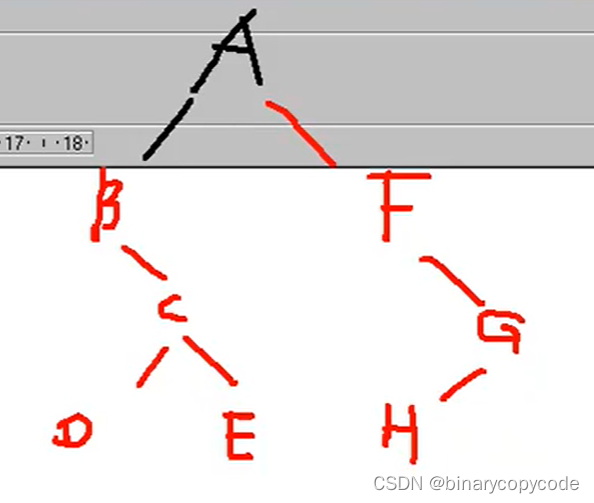
先序:ABCDEFGH
已知先序和后序求中序
和以上两种情况类似。
树的应用
- 树是数据库中数据组织的一种重要形式
- OS当中的子父进程的关系也是树
- 面向对象语言中类的继承关系
- 哈夫曼树
- B树
- B+树
- B*树
- 红黑树
- AVL树
相关文章:

树及其遍历
文章目录 树树定义专业术语树分类 二叉树分类存储连续存储(完全二叉树)链式存储一般树的存储森林的存储 线索二叉树哈夫曼树构造步骤 遍历先序遍历中序遍历后续遍历 链式二叉树遍历具体代码已知两种遍历序列求原始二叉树已知先序和中序求后序已知中序和后…...

Qt报错解决办法
anaconda环境安装qt报错解决办法 报错:thresholdGap: 20 pointsShape: 164142 qt.qpa.plugin: Could not find the Qt platform plugin “wayland” in “/home/tianhailong/anaconda3/envs/edge_algorithm/lib/python3.8/site-packages/cv2/qt/plugins” This app…...

Python(四十七)列表对象的创建
❤️ 专栏简介:本专栏记录了我个人从零开始学习Python编程的过程。在这个专栏中,我将分享我在学习Python的过程中的学习笔记、学习路线以及各个知识点。 ☀️ 专栏适用人群 :本专栏适用于希望学习Python编程的初学者和有一定编程基础的人。无…...
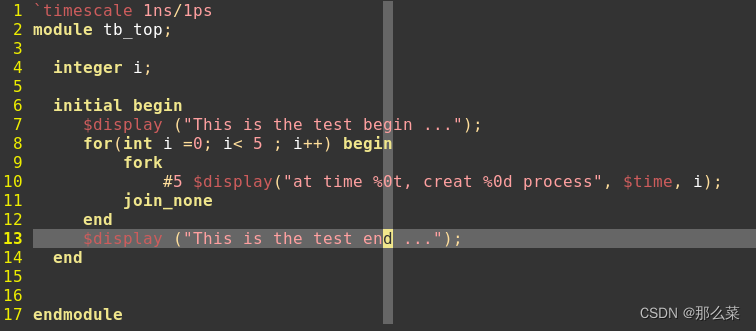
#systemverilog# 说说Systemverilog中《automatic》那些事儿
前面我们学习了有关systemverilog语言中有关《static》的一些知识,同static 关系比较好的哥们,那就是 《automatic》。今天,我们了解认识一下。 在systemveriog中,存在三种并发执行语句,分别是fork..join,fork...join_any和fork..join_none,其中只有fork...join_none不…...

C/C++ 动态内存分配与它的指针变量
一、什么是内存的动态分配 全局变量分配在内存中的静态存储区。局部变量(包括形参)分配在内存中的动态存储区,这个存储区是一个称为栈的区域。除此之外,C语言还允许建立内存动态分配区域,以存放一些临时用的数据&…...

UE5初学者快速入门教程
虚幻引擎是一系列游戏开发工具,能够将 2D 手机游戏制作为 AAA 游戏机游戏。虚幻引擎 5 用于开发下一代游戏,包括Senuas Saga: Hellblade 2、Redfall(来自 Arkane Austin 的合作射击游戏)、Dragon Quest XII: The Flames of Fate、…...

论文笔记--FEDERATED LEARNING: STRATEGIES FOR IMPROVING COMMUNICATION EFFICIENCY
论文笔记--FEDERATED LEARNING: STRATEGIES FOR IMPROVING COMMUNICATION EFFICIENCY 1. 文章简介2. 文章概括3 文章重点技术3.1 联邦学习(federated learning, FL)3.2 Structured updates3.3 Sketched Update 4. 文章亮点5. 原文传送门 1. 文章简介 标题:FEDERATE…...
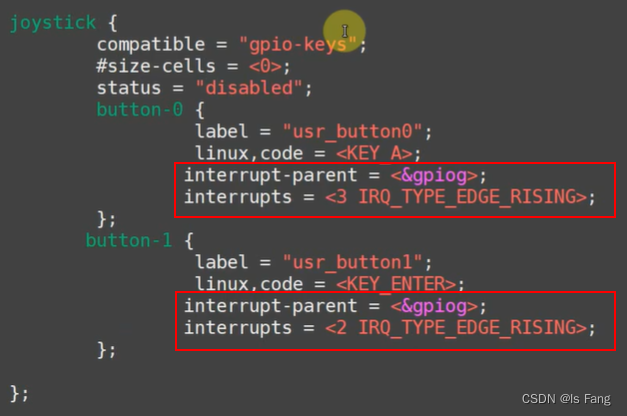
STM32MP157驱动开发——按键驱动(异步通知)
文章目录 “异步通知 ”机制:信号的宏定义:信号注册 APP执行过程驱动编程做的事应用编程做的事异步通知方式的按键驱动程序(stm32mp157)button_test.cgpio_key_drv.cMakefile修改设备树文件编译测试 “异步通知 ”机制: 信号的宏定义&#x…...

医疗器械维修工程师心得
彩虹医械维修技能班9月将开展本年第三期长期班,目前咨询人员也陆续多了起来,很多刚了解到医疗行业的,自身也没有多少相关的基础,在咨询时会问到没有基础能否学的会? 做了这行业的都知道,无论多么复杂的设备…...
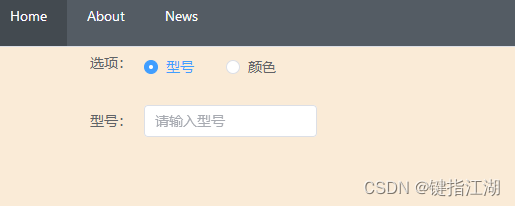
Vue3 Radio单选切换展示不同内容
Vue3 Radio单选框切换展示不同内容 环境:vue3tsviteelement plus 技巧:v-if,v-show的使用 实现功能:点击单选框展示不同的输入框 效果实现前的代码: <template><div class"home"><el-row …...
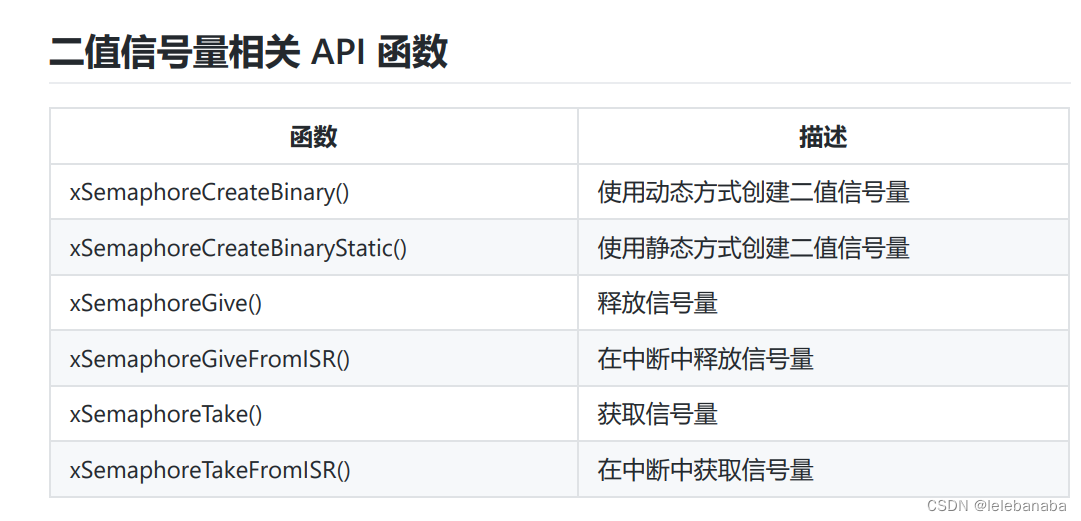
FreeRTOS之二值信号量
什么是信号量? 信号量(Semaphore),是在多任务环境下使用的一种机制,是可以用来保证两个或多个关键代 码段不被并发调用。 信号量这个名字,我们可以把它拆分来看,信号可以起到通知信号的作用&am…...

ChatGPT API进阶调用指南
原文:ChatGPT API进阶调用指南 ChatGPT API 进阶调用指南 ChatGPT API 是基于 OpenAI 的 GPT模型的一个强大工具,可以用于构建各种对话式应用。以下是一些使用 Markdown 语法的进阶调用指南,以帮助您更好地利用 ChatGPT API。 设置用户角色…...

人工智能术语翻译(四)
文章目录 摘要MNOP 摘要 人工智能术语翻译第四部分,包括I、J、K、L开头的词汇! M 英文术语中文翻译常用缩写备注Machine Learning Model机器学习模型Machine Learning机器学习ML机器学习Machine Translation机器翻译MTMacro Average宏平均Macro-F1宏…...

kubernetes持久化存储卷
kubernetes持久化存储卷 kubernetes持久化存储卷一、存储卷介绍二、存储卷的分类三、存储卷的选择四、本地存储卷之emptyDir五、本地存储卷之 hostPath六、网络存储卷之nfs七、PV(持久存储卷)与PVC(持久存储卷声明)7.1 认识pv与pvc7.2 pv与pvc之间的关系7.3 实现nfs类型pv与pvc…...
【Rust笔记】意译解构 Object Safety for trait
意译解构Object Safety for trait 借助【虚表vtable】对被调用成员函数【运行时内存寻址】的作法允许系统编程语言Rust模仿出OOP高级计算机语言才具备的【专用多态Ad-hoc Polymorphism】特性。 计算机高级语言中的“多态”术语是一个泛指。它通常可被细化为 基于继承关系的“子…...

Spring Boot单元测试入门指南
Spring Boot单元测试入门指南 JUnit是一个成熟和广泛应用的Java单元测试框架,它提供了丰富的功能和灵活的扩展机制,可以帮助开发人员编写高质量的单元测试。通过JUnit,开发人员可以更加自信地进行重构、维护和改进代码,同时提高代…...

《面试1v1》如何能从Kafka得到准确的信息
🍅 作者简介:王哥,CSDN2022博客总榜Top100🏆、博客专家💪 🍅 技术交流:定期更新Java硬核干货,不定期送书活动 🍅 王哥多年工作总结:Java学习路线总结…...

2023秋招面试题持续更新中。。。
目录 1.八股文渐进式MVVM三次握手,四次挥手viteajax组件化和模块化虚拟dom原理流程浏览器内核浏览器渲染过程回流和重绘nextTick 2.项目相关1.声明式导航和编程式导航重写push和replace方法:性能优化图片懒加载路由懒加载 http请求方式 1.八股文 渐进式…...
Java | 数组排序算法
一、冒泡排序 冒泡排序的基本思想是对比相邻的元素值,如果满足条件就交换元素值,把较小的元素移到数组前面,把较大的元素移到数组后面(也就是交换两个元素的位置),这样较小的元素就像气泡一样从底部升到顶…...

android studio 连接SQLite数据库并实现增删改查功能
功能代码及调试代码 package com.example.bankappdemo;import android.annotation.SuppressLint; import android.content.ContentValues; import android.database.sqlite.SQLiteDatabase; import android.os.Bundle; import android.util.Log; import android.view.View; im…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...
