如何使用Python进行数据挖掘?
使用Python进行数据挖掘需要掌握以下几个关键步骤:
-
数据收集:首先,你需要获取你要进行数据挖掘的数据。可以从公共数据集、API、数据库等各种来源收集数据。
-
数据清洗:清洗数据是一个重要的步骤,它包括去除重复数据、处理缺失值、处理异常值、标准化数据等操作,以确保数据的质量和一致性。
-
数据预处理:在数据挖掘之前,通常需要进行一些预处理的操作。例如,对文本数据进行分词、去除停用词、提取特征等。
-
特征选择:选择合适的特征对于数据挖掘的效果至关重要。可以使用统计方法、相关性分析、特征重要性评估等手段来选择特征。
-
模型选择和训练:根据你的问题和数据类型,选择适合的数据挖掘模型,如分类、聚类、回归等。使用Python中常用的机器学习库,如scikit-learn、TensorFlow、PyTorch等进行模型的训练和优化。
-
模型评估和验证:使用交叉验证、混淆矩阵、精确率、召回率等指标评估模型的性能。根据评估结果对模型进行调整和改进。
-
结果解释和可视化:将数据挖掘的结果进行解释和可视化,以便更好地理解数据和模型的输出。
使用Python进行数据挖掘可以借助一些流行的库和工具,如Pandas、NumPy、Matplotlib、Seaborn、Scikit-learn等。这些库提供了丰富的功能和工具,极大地简化了数据挖掘的过程。同时,网上也有很多关于使用Python进行数据挖掘的教程和示例代码,可以帮助你更好地上手。
相关文章:

如何使用Python进行数据挖掘?
使用Python进行数据挖掘需要掌握以下几个关键步骤: 数据收集:首先,你需要获取你要进行数据挖掘的数据。可以从公共数据集、API、数据库等各种来源收集数据。 数据清洗:清洗数据是一个重要的步骤,它包括去除重复数据、…...

若依-前台无法正常启动,npm run dev失败
问题场景: 使用若依Vue前端分离版-基于SpringBoot的权限管理系统进行实战。 问题描述与解决 拉取若依项目后,根据官方开发文档(项目readme文档)进行依赖下载安装后,启动失败。 出现以下几个问题: 运行n…...

Spring之IoC源码分析及设计思想(一)——BeanFactory
关于Spring的IOC Spring 是一个开源的 Java 平台,它提供了一种简化应用程序开发的框架。它是一个分层的框架,包括两个主要的内核:控制反转(IOC)和面向切面编程(AOP)。IOC 允许应用程序将组件之…...
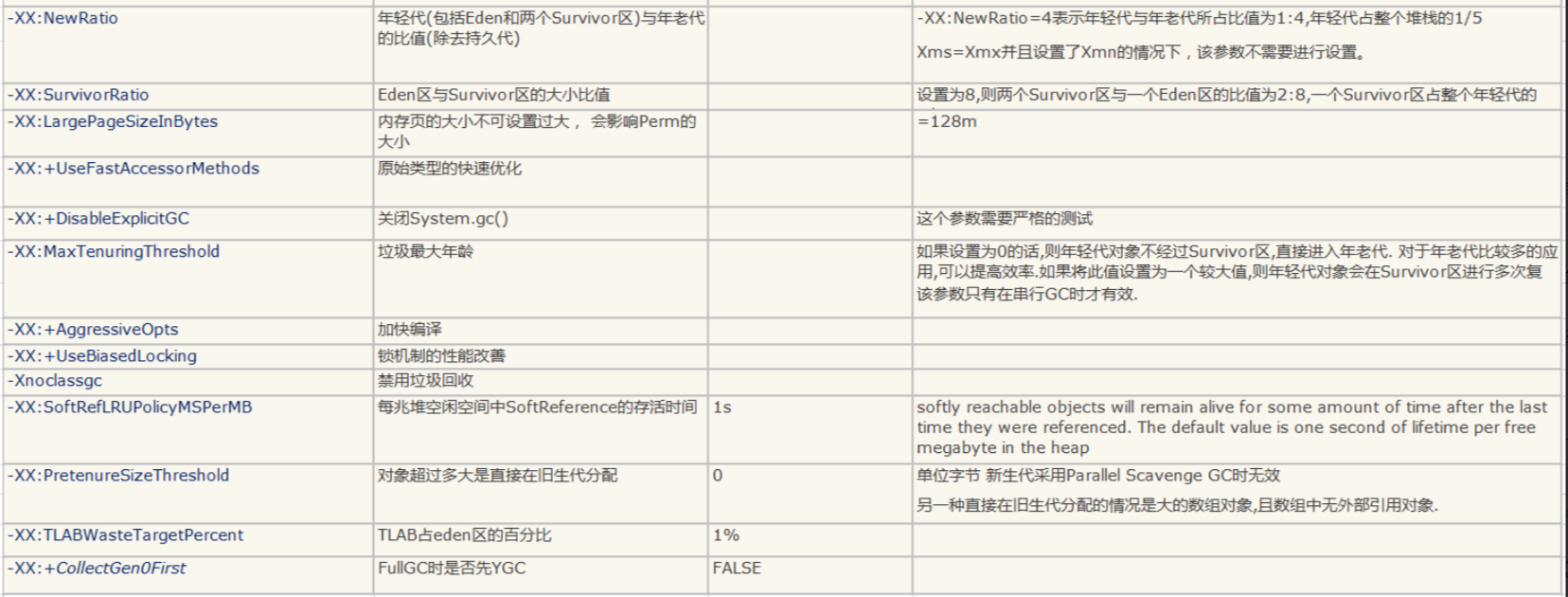
⛳ 面向对象面试题
面向对象面试题目录 ⛳ 面向对象面试题🚜 一,成员变量,局部变量,类变量存储在内存的什么地方?🐾 1.1,类变量(静态成员变量)📝 1.2,成员变量⭐ 1.3…...

Java中使用Gson操作json数据
Java中使用Gson操作json数据 引入依赖 <dependency><groupId>com.google.code.gson</groupId><artifactId>gson</artifactId><version>2.9.0</version></dependency>Gson工具类 package cn.test.util;import com.google.gso…...

Verilog语法学习——LV10_使用函数实现数据大小端转换
LV10_使用函数实现数据大小端转换 题目来源于牛客网 [牛客网在线编程_Verilog篇_Verilog快速入门 (nowcoder.com)](https://www.nowcoder.com/exam/oj?page1&tabVerilog篇&topicId301) 题目 描述 在数字芯片设计中,经常把实现特定功能的模块编写成函数&…...

Leetcode-每日一题【剑指 Offer II 009. 乘积小于 K 的子数组】
题目 给定一个正整数数组 nums和整数 k ,请找出该数组内乘积小于 k 的连续的子数组的个数。 示例 1: 输入: nums [10,5,2,6], k 100输出: 8解释: 8 个乘积小于 100 的子数组分别为: [10], [5], [2], [6], [10,5], [5,2], [2,6], [5,2,6]。 需要注意的是 [10,5,2]…...

html/javascript-表格的创建和使用
html中表格的创建和使用 一 摘要二 使用html table标签创建表格(在html文件中)三 使用javascript创建表格(在js文件中)四 表格属性的设置:4.1. 右边框的设置:4.2. 只给表格单元格加右边框4.3. 动态设置右边…...
)
[点微]同城原生微信小程序 小程序原生版 1.0.7(tom_xiaofenlei)
注意!!!这是点微后出的原生版小程序!!! 依赖点微同城分类主插件、点微同城小程序后端插件!!! 【以下为模块路径】 同城首页 pages/index/index 个人中心 pages/index/my 好店首页 pages/module/tcshop 商城首页 pages/module/tcmall 抢购首页 pages/module/tcqianggou…...
JDBC Some Templates
JDBCTemplate 是Spring对JDBC的封装,使用JDBCTemplate方便实现对数据的操作。 <!-- orm:Object relationship mapping m对象 关系 映射-->引入依赖 <!-- 基于Maven依赖的传递性,导入spring-content依赖即可导入当前所需的所有…...

dubbo启动指定ip不使用docker虚拟网络ip
java -D 配置系统属性 # 启动时加参数 -DDUBBO_IP_TO_REGISTRY 192.168.1.1 该ip为dubbo所在服务器的公网ip即可。 java -jar myDubboRpc-api.jar -DDUBBO_IP_TO_REGISTRY 192.168.1.1 # xjar启动 nohup ./xjar java -DDUBBO_IP_TO_REGISTRY11.22.33.44 -XX:UseG1GC -jar …...

Bobo String Construction
登录—专业IT笔试面试备考平台_牛客网 题目大意:给出一字符串t,求一个长为n的字符串,使tst中包含且仅包含两个t 1<n<1000;测试样例组数<1000 思路:一开始很容易想到如果t里有1,s就全0,否则s就全…...

基于java在线个人网站源码设计与实现
摘 要 随着社会及个人社交应用平台的飞速发展,人们的沟通成本逐渐降低,互联网信息的普及也进一步提升了人们对于信息的需求度,通过建立个人网站的方式来展示自己的生活信息同时利用平台结交新的朋友,借助个人网站平台的搭建不仅可…...
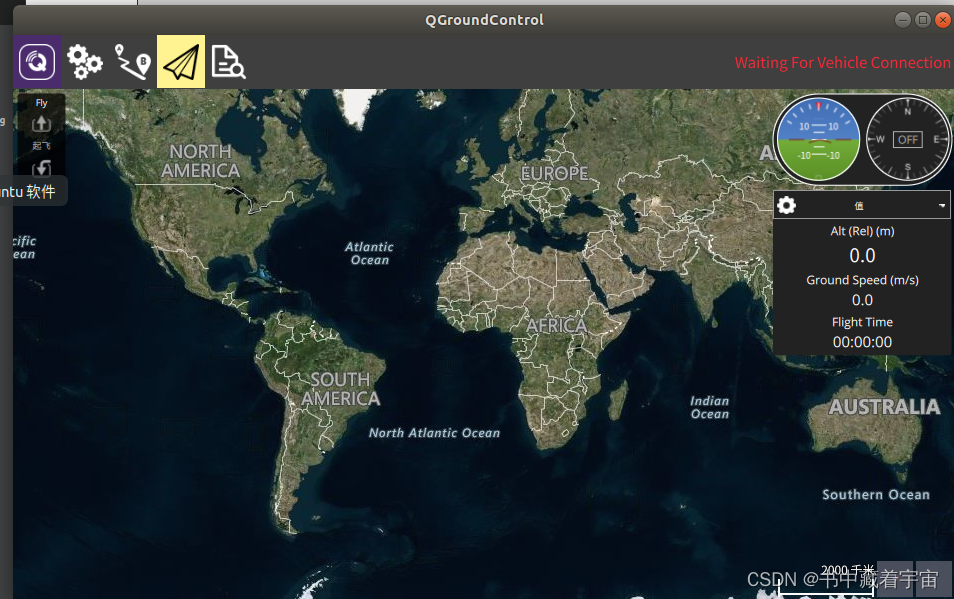
Ubuntu18.04下编译qgc源码
写在前面 在下载前必须说明,根据你的qgc源码版本进行下载,有的源码必须要求Qt是5.15版本以上。 个人所使用开发软件 版本QT5.12.9qgc源码V4.0Ubuntu18.04 QT下载 (1)我们可以去官网下载官网下载地址具体的下载方法这里不用多说&a…...

Ros2_windows_install的学习笔记
Ros2_windows_install安装 Iron安装 iex ((New-Object System.Net.WebClient).DownloadString(https://raw.githubusercontent.com/scottcandy34/ros2_windows_install/main/ros2_iron.ps1))启动Iron C:\dev\ros2_iron\local_setup.bat...

5、Kubernetes核心技术 - Controller控制器工作负载
目录 一、Deployments - 控制器应用 二、Deployment升级回滚和弹性收缩 2.1、创建一个 1.14 版本的 pod 2.2、应用升级 2.3、查看升级状态 2.4、查看历史版本 2.5、应用回滚 2.6、弹性伸缩 三、StatefulSet - 有状态应用 四、DaemonSet - 守护进程 五、Job - 单次任…...
)
【java设计模式】创建型模式介绍(工厂模式、抽象工厂模式、单例模式、建造者模式、原型模式)
文章目录 简介一、工厂模式介绍案例 二、抽象工厂模式介绍案例 三、单例模式介绍案例 四、建造者模式介绍案例 五、原型模式介绍案例 简介 本文介绍Java设计模式中创建型模式的五种 一、工厂模式 工厂模式(Factory Pattern)是 Java 中最常用的设计模式…...
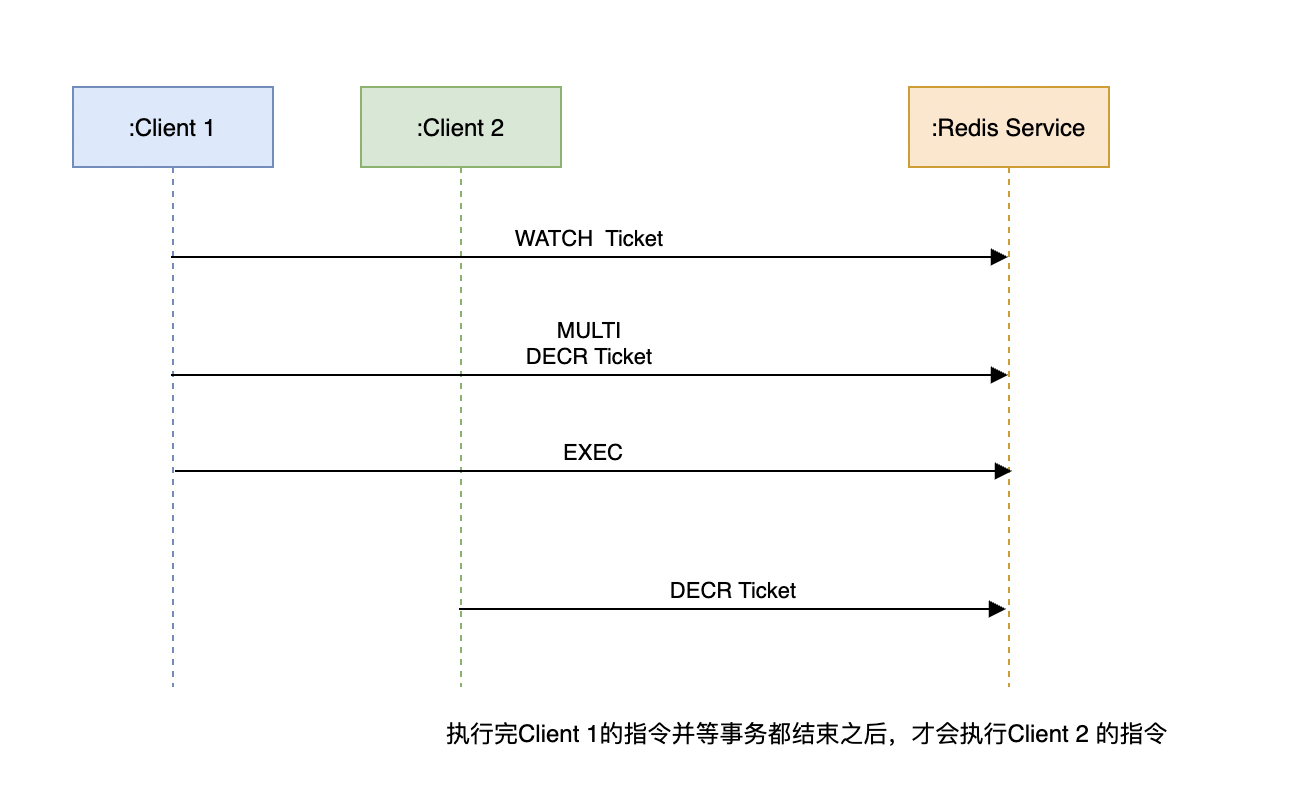
Redis系列:Redis 的事务机制
1 复习下何为事务机制? Transaction(事务)是计算机的特有术语,它一般指单个逻辑工作单位,由一系列的操作组合而成,在这些操作执行的时候,要么都执行成功,要么都不执行,防…...

动静态网页、Django创建表关系、Django框架的请求生命周期流程图
一、request对象的几个方法 在视图函数中写方法的时候,都会有一个形参requestdef index(request):passrequest.method # GET POST request.GET.get() # 它获取最后一个元素值 request.GET.getlist() # 获取到所有的request.POST.get() # 它获取最后一个元素值 req…...

神经网络的初始化方法
文章目录 1、随机初始化2、Xavier初始化3、He初始化4、权重预训练初始化5、零初始化 对于神经网络的训练过程中,合适的参数初始化方法有助于更好的处理梯度消失和梯度爆炸问题。通常有以下几种初始化方法: 1、随机初始化 随机初始化(Random…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...
