红宝书第二十一讲:详解JavaScript的模块化(CommonJS与ES Modules)
红宝书第二十一讲:详解JavaScript的模块化(CommonJS与ES Modules)
资料取自《JavaScript高级程序设计(第5版)》。
查看总目录:红宝书学习大纲
一、模块化的意义:分而治之
模块化解决代码依赖混乱、命名冲突问题,核心思想:
- 每个文件为一个独立模块
- **导出(export)**需要暴露的功能
- **导入(import)**其他模块的功能
二、CommonJS:服务端的模块化方案
CommonJS设计用于服务器环境(如Node.js),特性:
- 同步加载 → 适合本地文件系统 1
- 使用
require()导入,module.exports导出 2
示例1:导出对象
// math.js
function add(a, b) { return a + b; }
module.exports = { add }; // 导出模块功能 [^5]// main.js
const math = require('./math.js'); // 导入模块 [^6]
console.log(math.add(3, 5)); // 输出8
示例2:导出类或实例
// User.js
class User { /* ... */ }
module.exports = User; // 导出类 [^5]// app.js
const User = require('./User.js');
const user = new User();
关键特点:导出的是对象或值的拷贝,多次导入会缓存结果 3
三、ES Modules(ESM):原生的浏览器支持
ES Modules是JavaScript官方标准,特性:
- 浏览器直接支持(需要
<script type="module">)43 - 导出用
export,导入用import
示例3:基本语法
// math.js
export const multiply = (a, b) => a * b;// main.js
import { multiply } from './math.js';
console.log(multiply(3, 5)); // 输出15
示例4:导出默认值
// config.js
const API_KEY = '12345abc';
export default API_KEY; // 默认导出// app.js
import key from './config.js'; // 默认导入不使用大括号
关键特点:导出的是引用,动态绑定,值更新影响所有导入方 3
四、对比CommonJS与ES Modules
| 特征 | CommonJS | ES Modules |
|---|---|---|
| 运行环境 | Node.js(服务器端)1 | 浏览器原生支持+现代Node 4 |
| 加载方式 | 同步(立即执行)1 | 异步(按需加载)3 |
| 导出内容 | 值的拷贝(静态)2 | 值的引用(动态)3 |
| 语法 | module.exports / require | export / import |
五、现代工具链:模块打包与转换
由于浏览器兼容问题,常用工具:
- Webpack/Babel → 将ESM/CommonJS转为兼容代码 5
- SystemJS → 动态加载多种格式模块(包括ESM)5

目录:总目录
上篇文章:红宝书第二十讲:详解JavaScript的Proxy与Reflect
下篇文章:红宝书第二十二讲:详解JavaScript类型化数组与二进制数据处理
脚注
《JavaScript高级程序设计(第5版)》详解CommonJS语法与Node.js的关系 ↩︎ ↩︎ ↩︎
《JavaScript高级程序设计(第5版)》演示CommonJS导出类与实例的方式 ↩︎ ↩︎
《JavaScript高级程序设计(第5版)》描述模块加载器的依赖图与执行顺序 ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
《JavaScript高级程序设计(第5版)》的目录指明ES Modules为原生标准 ↩︎ ↩︎
《JavaScript高级程序设计(第5版)》指出SystemJS支持动态加载ESM等模块格式 ↩︎ ↩︎
相关文章:

红宝书第二十一讲:详解JavaScript的模块化(CommonJS与ES Modules)
红宝书第二十一讲:详解JavaScript的模块化(CommonJS与ES Modules) 资料取自《JavaScript高级程序设计(第5版)》。 查看总目录:红宝书学习大纲 一、模块化的意义:分而治之 模块化解决代码依赖混…...

github 页面超时解决方法
github 页面超时解决方法 每次好不容易找到github项目代码之后,满心欢喜打开却是个无法访问,心顿时又凉了半截,现在有方法可以访问github啦 快来学习 打开浏览器插件(Edge浏览器) 搜索iLink插件 并安装 打开插件 填…...

前端 vue 项目上线前操作
目录 一、打包分析 二、CDN加速 三、项目部署 1. 打包部署 2. nginx 解决 history 刷新 404 问题 3. nginx配置代理解决生产环境跨域问题 一、打包分析 项目编写完成后,就需要部署到服务器上供他人访问。但是在此之前,我们可以先预览项目的体积大…...

矩阵对角化→实对称矩阵的对角化→实对称半正定矩阵的对角化
上篇:特征值→相似矩阵→矩阵对角化(特征值分解) 实对称矩阵正交对角化 实对称矩阵是指满足 A A T \bm A \bm A^{\mathsf {T}} AAT的矩阵,其中 A T \bm A^{\mathsf T} AT是 A \bm A A的转置矩阵。对称矩阵的特征值均为实数。实…...

vue: easy-cron扩展-更友好地显示表达式
我们一个批处理调度系统里要用到cron表达式,于是就在网上找到一个现成的组件easy-cron,采用后发现,它的配置界面还是很直观的,但显示时直接显示cron表达式,这对业务人员很不友好,所以,我们就扩展…...

移动零+复写零+快乐数+盛最多水的容器+有效三角形的个数
前言 2025.3.31,今天开始每日五道算法题,今天的算法题如标题! 双指针算法 在做今天的算法题之前,先来介绍一下今天会用到的算法! 双指针算法分为了两种常见的形式:对撞指针和快慢指针! 对撞…...
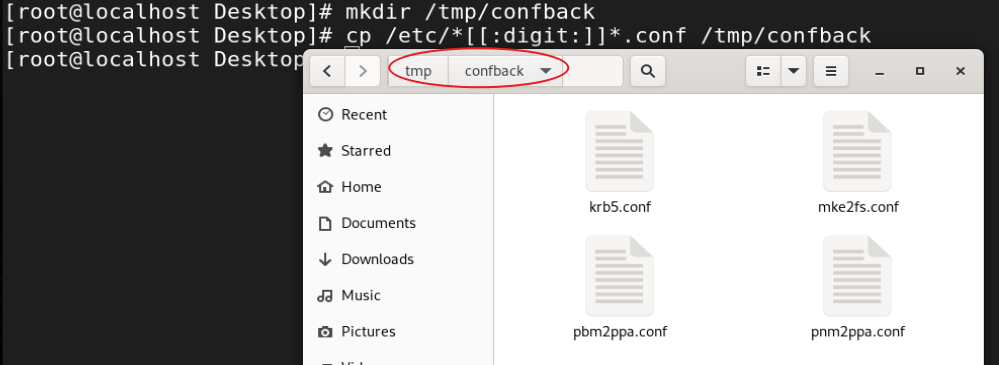
Linux中常用的文件管理命令
一、文件和目录的建立 文件 touch命令 单一文件的创建 当按下回车后我们就可以在桌面获得一个名字叫file的文件 [rootlocalhost Desktop]# touch file 同步文件访问时间和文件修改时间 由上两图可知touch file这个命令还可以把文件访问时间和文件修改时间变成touch file命…...

Root Cause Analysis in Microservice Using Neural Granger Causal Discovery
Root Cause Analysis in Microservice Using Neural Granger Causal Discovery 出处:AAAI 24 摘要 近年来,微服务因其可扩展性、可维护性和灵活性而在 IT 运营中得到广泛采用。然而,由于微服务中的复杂关系,当面临系统故障时,站点可靠性工程师 (SRE) 很难查明根本原…...

学习笔记—数据结构—二叉树(链式)
目录 二叉树(链式) 概念 结构 初始化 遍历 前序遍历 中序遍历 后序遍历 层序遍历 结点个数 叶子结点个数 第k层结点个数 深度/高度 查找值为x的结点 销毁 判断是否为完整二叉树 总结 头文件Tree.h Tree.c 测试文件test.c 补充文件Qu…...

微前端 - 以无界为例
一、微前端核心概念 微前端是一种将单体前端应用拆分为多个独立子应用的架构模式,每个子应用可独立开发、部署和运行,具备以下特点: 技术栈无关性:允许主应用和子应用使用不同框架(如 React Vue)。独立部…...

DIskgenius使用说明
文章目录 一、概述1. 软件简介2. 系统要求 二、核心功能1. 分区管理(1) 查看磁盘分区(2) 创建与删除分区(3) 调整分区大小(4) 格式化分区 2. 数据恢复(1) 恢复已删除文件(2) 恢复丢失分区(3) 恢复误格式化分区 3. 磁盘复制(1) 克隆磁盘(2) 磁盘镜像 4. 文件操作(1) 文件复制与移…...

深入理解指针5
sizeof和strlen的对比 sizeof的功能 **sizeof是**** 操作符****,用来**** 计算****变量或类型或数组所占**** 内存空间大小****,**** 单位是字节,****他不管内存里是什么数据** int main() {printf("%zd\n", sizeof(char));p…...

一文详解QT环境搭建:Windows使用CLion配置QT开发环境
在当今的软件开发领域,跨平台应用的需求日益增长,Qt作为一款流行的C图形用户界面库,因其强大的功能和易用性而备受开发者青睐。与此同时,CLion作为一款专为C/C打造的强大IDE,提供了丰富的特性和高效的编码体验。本文将…...

NE 综合实验3:基于 IP 配置、链路聚合、VLAN 管理、路由协议及安全认证的企业网络互联与外网访问技术实现(H3C)
综合实验3 实验拓扑 设备名称接口IP地址R1Ser_1/0与Ser_2/0做捆绑MP202.100.1.1/24G0/0202.100.2.1/24R2Ser_1/0与Ser_2/0做捆绑MP202.100.1.2/24G0/0172.16.2.1/24G0/1172.16.1.1/24G0/2172.16.5.1/24R3G5/0202.100.2.2/24G0/0172.16.2.2/24G0/1172.16.3.1/24G0/2172.16.7.1/…...
:机器学习中的“真相”基准)
Ground Truth(真实标注数据):机器学习中的“真相”基准
Ground Truth:机器学习中的“真相”基准 文章目录 Ground Truth:机器学习中的“真相”基准引言什么是Ground Truth?Ground Truth的重要性1. 模型训练的基础2. 模型评估的标准3. 模型改进的指导 获取Ground Truth的方法1. 人工标注2. 众包标注…...

双重token自动续期解决方案
Token自动续期实现方案详解 Token自动续期是提升用户体验和保障系统安全的关键机制,其核心在于无感刷新和安全可控。以下从原理、实现方案、安全措施和最佳实践四个维度展开说明: 一、核心原理:双Token机制 Token自动续期通常采用 Access …...

我与数学建模之启程
下面的时间线就是从我的大二上开始 9月开学就迎来了本科阶段最重要的数学建模竞赛——国赛,这个比赛一般是在9月的第二周开始。 2021年国赛是我第一次参加国赛,在报名前我还在纠结队友,后来经学长推荐找了另外两个学长。其实第一次国赛没啥…...

多段圆弧拟合离散点实现切线连续
使用多段圆弧来拟合一个由离散点组成的曲线,并且保证切线连续。也就是说,生成的每一段圆弧之间在连接点处必须有一阶导数连续,也就是切线方向相同。 点集分割 确保每个段的终点是下一段的起点,相邻段共享连接点,避免连接点位于数…...

烧结银:解锁金刚石超强散热潜力
烧结银:解锁金刚石超强散热潜力 在材料科学与热管理领域,金刚石凭借超高的热导率,被誉为 “散热之王”,然而,受限于其特殊的性质,金刚石在实际应用中难以充分发挥散热优势。而烧结银AS9335的出现&#x…...

【蓝桥杯】第十四届C++B组省赛
⭐️个人主页:小羊 ⭐️所属专栏:蓝桥杯 很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~ 目录 试题A:日期统计试题B:01串的熵试题C:冶炼金属试题D:飞机降落试题E:接…...

企业级海外网络专线行业应用案例及服务商推荐
在全球化业务快速发展的今天,传统网络技术已难以满足企业需求。越来越多企业开始选择新型海外专线解决方案,其中基于SD-WAN技术的企业级海外网络专线备受关注。这类服务不仅能保障跨国数据传输,还能根据业务需求灵活调整网络配置。接下来我们…...

阿里云服务器安装docker以及mysql数据库
(1) 官方下载路径 官方下载地址: Index of linux/static/stable/x86_64/阿里云镜像地址: https://mirrors.aliyun.com/docker-ce/下载最新的 Docker 二进制文件:wget https://download.docker.com/linux/static/stable/x86_64/docker-20.10.23.tgz登录到阿里云服务…...
)
力扣经典算法篇-5-多数元素(哈希统计,排序,摩尔投票法)
题干: 给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。 你可以假设数组是非空的,并且给定的数组总是存在多数元素。 示例 1: 输入:nums [3,2,3] 输出&…...

axios介绍以及配置
Axios 是一个基于 Promise 的 HTTP 客户端,用于浏览器和 Node.js 环境中进行 HTTP 请求。 一、特点与基本用法 1.特点 浏览器兼容性好:能在多种现代浏览器中使用,包括 Chrome、Firefox、Safari 等。支持 Promise API:基于 Prom…...

深入解析:HarmonyOS Design设计语言的核心理念
深入解析:HarmonyOS Design设计语言的核心理念 在当今数字化迅速发展的时代,用户对操作系统的体验要求越来越高。华为的HarmonyOS(鸿蒙操作系统)应运而生,旨在为用户提供全场景、全设备的智慧体验。其背后的设计语言—…...

大数据技术之Scala:特性、应用与生态系统
摘要 Scala 作为一门融合面向对象编程与函数式编程范式的编程语言,在大数据领域展现出独特优势。本文深入探讨 Scala 的核心特性,如函数式编程特性、类型系统以及与 Java 的兼容性等。同时,阐述其在大数据处理框架(如 Apache Spa…...
:竞价指标剖析与流量对接要点)
程序化广告行业(47/89):竞价指标剖析与流量对接要点
程序化广告行业(47/89):竞价指标剖析与流量对接要点 大家好!一直以来,我都希望能和大家一同深入探索程序化广告行业的奥秘,这也是我持续撰写这一系列博客的动力。今天,咱们接着来剖析程序化广告…...

dfs记忆化搜索刷题 + 总结
文章目录 记忆化搜索 vs 动态规划斐波那契数题解代码 不同路径题解代码 最长递增子序列题解代码 猜数字大小II题解代码 矩阵中的最长递增路径题解代码 总结 记忆化搜索 vs 动态规划 1. 记忆化搜索:有完全相同的问题/数据保存起来,带有备忘录的递归 2.记忆…...

vue2 全局封装axios统一管理api
在vue项目中,经常会使用到axios来与后台进行数据交互,axios丰富的api满足我们基本的需求。但是对于项目而言,每次都需要对异常进行捕获或者处理的话,代码会很繁重冗余。我们需要将其公共部分封装起来,比如异常处理&…...

大模型有哪些算法
大模型(Large-scale Models)通常指参数量大、架构复杂、在特定任务或领域表现出色的深度学习模型。这些模型的算法核心往往基于Transformer 架构及其变体,同时结合了大规模数据、硬件加速和优化技巧。以下是当前主流大模型及其核心算法的分类…...
