Eigen库几何模块深度解析与实践指南
Eigen库几何模块深度解析与实践指南
a. Eigen几何模块概述
i. 几何模块的核心功能
在三维空间中,几何变换是描述物体位置和姿态变化的基础,其数学基础涵盖了线性代数中的矩阵运算等知识。Eigen库的几何模块为这些变换提供了高效且便捷的实现方式。
旋转、平移和缩放是三维空间中最基本的几何操作。旋转操作可通过旋转矩阵、旋转向量或四元数来表示。例如,旋转向量(轴角)定义了绕某一轴逆时针旋转一定角度,在Eigen中用Eigen::AngleAxisd表示。平移操作则使用平移向量,在Eigen里对应Eigen::Vector3d。缩放操作可对物体在各个坐标轴上进行比例缩放。
齐次坐标表示方法是将三维空间中的点和向量扩展到四维,通过引入一个额外的维度,使得旋转、平移和缩放等操作可以统一用矩阵乘法来实现。在机器人学中,刚体的运动就可以看作是一系列的旋转和平移变换的组合。例如,机器人手臂的运动可以通过不断更新其末端执行器的位姿来实现,而位姿的更新就涉及到旋转和平移操作。
在SLAM(同时定位与地图构建)和计算机视觉领域,几何模块也有着广泛的应用。在SLAM中,需要不断地估计机器人的位姿和构建环境地图,这就需要对传感器数据进行旋转和平移变换。在计算机视觉中,图像的配准、三维重建等任务也离不开几何变换。
ii. 模块架构与头文件组成
Eigen的Geometry模块有着清晰的类继承体系。它与Core模块紧密相关,Core模块提供了基本的矩阵和向量操作,而Geometry模块则在此基础上实现了各种几何变换。
Geometry模块中的核心类包括Isometry3d、Quaterniond等。Isometry3d表示三维空间中的等距变换,即只包含旋转和平移的变换,它是一个4x4的变换矩阵。Quaterniond则是四元数的表示,四元数在表示旋转时具有避免万向节锁等优点。
这些类的设计哲学是提供高效、易用且与数学概念紧密对应的接口。例如,Isometry3d的pretranslate()和rotate()方法可以方便地给平移部分和旋转矩阵赋值。同时,Geometry模块具有与OpenGL兼容的特性,这使得在进行图形渲染等操作时可以方便地与OpenGL进行交互。在使用时,只需要包含<Eigen/Geometry>头文件即可使用这些功能。
b. 核心数据结构与初始化方法
i. 旋转矩阵与旋转向量
在Eigen库中,Matrix3d和AngleAxisd是用于表示旋转的重要数据结构。Matrix3d代表一个3x3的双精度矩阵,常用于存储旋转矩阵;而AngleAxisd则以轴角的形式表示旋转,即绕某一轴旋转特定的角度。
以下是它们的构造方法及相关操作的代码示例:
#include <iostream>
#include <Eigen/Core>
#include <Eigen/Geometry>int main() {// 初始化旋转向量,绕Z轴旋转45度(M_PI/4弧度)Eigen::AngleAxisd rotation_vector(M_PI / 4, Eigen::Vector3d(0, 0, 1));// 将旋转向量转换为旋转矩阵Eigen::Matrix3d rotation_matrix = rotation_vector.matrix();// 也可以直接初始化旋转矩阵为单位矩阵Eigen::Matrix3d identity_matrix = Eigen::Matrix3d::Identity();std::cout << "Rotation Vector:" << std::endl;std::cout << rotation_vector.axis().transpose() << " * " << rotation_vector.angle() << std::endl;std::cout << "Rotation Matrix:" << std::endl;std::cout << rotation_matrix << std::endl;std::cout << "Identity Matrix:" << std::endl;std::cout << identity_matrix << std::endl;return 0;}
在上述代码中,首先使用AngleAxisd构造了一个绕Z轴旋转45度的旋转向量。通过调用.matrix()成员函数,可以将旋转向量转换为旋转矩阵。同时,使用Eigen::Matrix3d::Identity()初始化了一个单位矩阵。
从计算效率上看,旋转向量在存储和某些操作上更为紧凑,例如在插值等操作中,旋转向量的计算相对简单。而旋转矩阵在进行向量变换时,直接使用矩阵乘法,计算速度较快。因此,在不同的应用场景中,可以根据具体需求选择合适的表示方法。
ii. 四元数与变换矩阵
Quaterniond是Eigen库中用于表示四元数的类,它有四种常见的构造方式:
-
默认构造函数:Eigen::Quaterniond q1;,此时四元数初始化为单位四元数。
-
从系数构造:Eigen::Quaterniond q2(w, x, y, z);,其中w是实部,x、y、z是虚部。需要注意的是,在Eigen中,四元数的存储顺序是(x, y, z, w)。
-
从旋转矩阵构造:Eigen::Quaterniond q3(rotation_matrix);,可以直接从旋转矩阵初始化四元数。
-
从旋转向量构造:Eigen::Quaterniond q4(rotation_vector);,从旋转向量初始化四元数。
以下是结合Isometry3d实例,演示pretranslate()与rotate()方法链式调用的代码:
#include <iostream>
#include <Eigen/Core>
#include <Eigen/Geometry>int main() {// 初始化四元数,绕Z轴旋转45度Eigen::Quaterniond q(Eigen::AngleAxisd(M_PI / 4, Eigen::Vector3d(0, 0, 1)));// 初始化平移向量Eigen::Vector3d t(1, 2, 3);// 创建等距变换矩阵Eigen::Isometry3d T = Eigen::Isometry3d::Identity();// 链式调用pretranslate()和rotate()方法T.pretranslate(t).rotate(q);std::cout << "Transformation Matrix:" << std::endl;std::cout << T.matrix() << std::endl;return 0;}
在这段代码中,首先创建了一个四元数表示绕Z轴旋转45度,然后定义了一个平移向量。接着,使用Eigen::Isometry3d::Identity()初始化一个等距变换矩阵。通过链式调用pretranslate()和rotate()方法,将平移和旋转操作组合到变换矩阵中。最后输出变换矩阵。这种链式调用的方式使得代码更加简洁和易读。
c. 坐标变换与复合变换
i. 单次旋转变换实现
在Eigen库中,实现单次旋转变换有两种常见的范式:rotation_vectorv和rotation_matrixv,其中v是待变换的向量。这两种方式本质上都是将向量进行旋转操作,但在实现和使用场景上有所不同。
rotation_vectorv是基于旋转向量的变换方式。旋转向量以轴角的形式表示旋转,它在存储和某些操作上更为紧凑,适合用于插值等操作。而rotation_matrixv则是使用旋转矩阵进行变换,在进行向量变换时,直接使用矩阵乘法,计算速度较快。
以下是一个代码案例,展示了Z轴45度旋转对向量(1,0,0)的影响,并使用transpose()方法对输出进行可视化优化:
#include <iostream>#include <Eigen/Core>
#include <Eigen/Geometry>int main() {// 初始化旋转向量,绕Z轴旋转45度(M_PI/4弧度)Eigen::AngleAxisd rotation_vector(M_PI / 4, Eigen::Vector3d(0, 0, 1));// 将旋转向量转换为旋转矩阵Eigen::Matrix3d rotation_matrix = rotation_vector.matrix();// 定义待变换的向量Eigen::Vector3d v(1, 0, 0);// 使用旋转向量进行变换Eigen::Vector3d v_rotated_by_vector = rotation_vector * v;// 使用旋转矩阵进行变换Eigen::Vector3d v_rotated_by_matrix = rotation_matrix * v;std::cout << "Original Vector: " << v.transpose() << std::endl;std::cout << "Rotated by Vector: " << v_rotated_by_vector.transpose() << std::endl;std::cout << "Rotated by Matrix: " << v_rotated_by_matrix.transpose() << std::endl;return 0;
}
在上述代码中,首先定义了一个绕Z轴旋转45度的旋转向量,并将其转换为旋转矩阵。然后定义了待变换的向量v,分别使用旋转向量和旋转矩阵对其进行变换。最后使用transpose()方法将向量以行向量的形式输出,方便可视化。
ii. 复合变换矩阵构建
欧式变换矩阵是一种常见的复合变换矩阵,它包含了旋转和平移两种操作。在Eigen库中,Isometry3d类可以用于表示和构建欧式变换矩阵。
欧式变换矩阵的级联原理是将多个变换矩阵依次相乘,从而实现多个变换的组合。在Isometry3d类中,pretranslate()和translate()方法都可以用于设置平移部分,但它们的作用顺序不同。pretranslate()是在当前变换的基础上先进行平移操作,再进行后续的旋转等操作;而translate()则是在当前变换完成后再进行平移操作。
以下是一个演示包含旋转和平移的4x4矩阵构建过程的代码示例:
#include <iostream>
#include 相关文章:

Eigen库几何模块深度解析与实践指南
Eigen库几何模块深度解析与实践指南 a. Eigen几何模块概述 i. 几何模块的核心功能 在三维空间中,几何变换是描述物体位置和姿态变化的基础,其数学基础涵盖了线性代数中的矩阵运算等知识。Eigen库的几何模块为这些变换提供了高效且便捷的实现方式。 旋转、平移和缩放是三维…...

第十四届蓝桥杯大赛软件赛省赛C/C++ 大学 B 组(部分题解)
文章目录 前言日期统计题意: 冶炼金属题意: 岛屿个数题意: 子串简写题意: 整数删除题意: 总结 前言 一年一度的🏀杯马上就要开始了,为了取得更好的成绩,好名字写了下前年2023年蓝桥…...

C语言常见3种排序
主要是三种排序方法:冒泡排序、选择排序、插入排序。 文章目录 一、冒泡排序 1.代码: 2.工作原理: 3.具体过程: 二、选择排序 1.代码 2. 工作原理 3.具体过程: 三、插入排序 1.代码 2.工作原理 3.具体过程 总结 一、…...
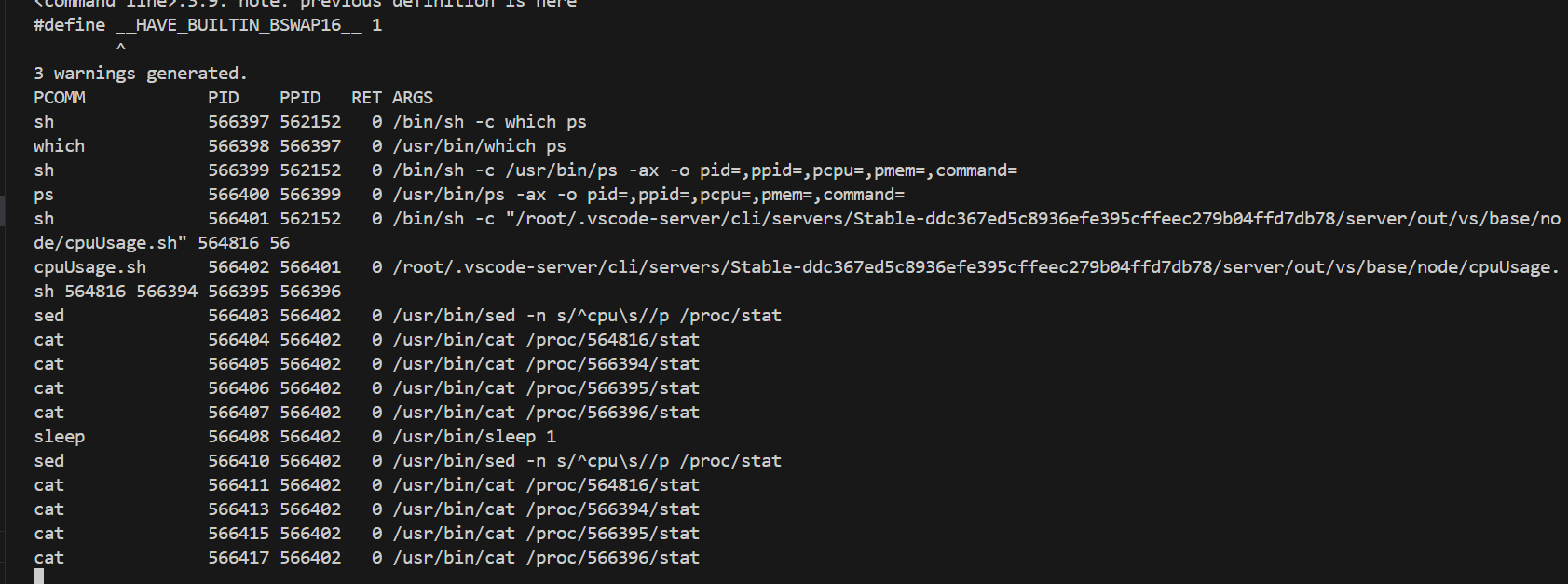
分析sys高问题的方法总结
一、背景 sys高的问题往往属于底层同学更需要关注的问题,sys高的问题往往表现为几种情况,一种是瞬间的彪高,一种是持续的彪高。这篇博客里,我们总结一下常用的分析方法和分析工具的使用来排查这类sys高的问题。 二、通过mpstat配…...

智谱发布AI Agent“AutoGLM沉思”,开启AI“边想边干”新时代
近日,智谱正式推出全新AI Agent产品——AutoGLM沉思,标志着人工智能从“思考”迈向“执行”的关键突破。该智能体不仅具备深度研究能力,还能自主完成实际操作,真正实现“边想边干”的智能化应用。 在演示环节,智谱展示…...

使用Leaflet对的SpringBoot天地图路径规划可视化实践-以黄花机场到橘子洲景区为例
目录 前言 一、路径规划需求 1、需求背景 2、技术选型 3、功能简述 二、Leaflet前端可视化 1、内容布局 2、路线展示 3、转折路线展示 三、总结 前言 在当今数字化与智能化快速发展的时代,路径规划技术已经成为现代交通管理、旅游服务以及城市规划等领域的…...

【小兔鲜】day02 Pinia、项目起步、Layout
【小兔鲜】day02 Pinia、项目起步、Layout 1. Pinia2. 添加Pinia到Vue项目3. 案例:Pinia-counter基础使用3.1 Store 是什么?3.2 应该在什么时候使用 Store? 4. Pinia-getters和异步action4.1 getters4.2 action如何实现异步 1. Pinia Pinia 是 Vue 的专…...

PyTorch 激活函数
激活函数是神经网络中至关重要的组成部分,它们为网络引入了非线性特性,使得神经网络能够学习复杂模式。PyTorch 提供了多种常用的激活函数实现。 常用激活函数 1. ReLU (Rectified Linear Unit) 数学表达式: PyTorch实现: torch.nn.ReLU(inplaceFals…...

魔塔社区使用llamafactory微调AI阅卷试题系统
启动 LLaMA-Factory 1. 安装 LLaMA-Factory 执行安装指令 git clone --depth 1 https://github.com/hiyouga/LLaMA-Factory.git cd LLaMA-Factory pip install -e ".[torch,metrics]"解决依赖冲突 如果遇到依赖冲突,可使用以下命令安装,不…...

Java面试黄金宝典29
1. 什么是普通索引和唯一性索引 定义: 普通索引:是最基本的索引类型,它为数据表中的某一列或多列建立索引,以加快数据的查询速度。它不限制索引列的值重复,允许存在多个相同的值。唯一性索引:在普通索引的基…...

git `switch` 命令详解与实用示例
文章目录 git switch 命令详解与实用示例git switch vs git checkoutgit switch 用法1. 切换到已有分支2. 创建并切换到新分支3. 切换到上一个分支4. 切换到远程分支(自动创建本地分支并追踪远程)5. 放弃未提交的修改并切换分支 总结 git switch 命令详解…...

Oracle中文一二三四排序【失败】
原文地址: Oracle数据库如何对中文的一二三四五六七八九十数进行正序排列排序_中文数字排序-CSDN博客 自定义排序函数 -- 自定义中文映射阿拉伯数字函数 CREATE OR REPLACE FUNCTION P_ORDER_CHINESE_TO_ARABIC(V_NUM VARCHAR2) RETURN NUMBER IS BEGIN-- 根据…...

AWS S3 和 Lambda 使用
目录: AWS概述 EMR Serverless AWS VPC及其网络 关于AWS网络架构的思考 AWS S3 和 Lambda 使用 本文将通过一个实例来说明如何使用 AWS S3 和 Lambda。 使用场景:通过代码将文件上传到S3,该文件需要是公开访问的,并对上传的文件进…...

Mysql 在什么样的情况下会产生死锁?
在 MySQL 中,死锁是指两个或多个事务相互等待对方释放锁,导致所有相关事务无法继续执行的情况。死锁会影响数据库的并发性能,因此需要及时检测并处理。假设有两个事务 T1 和 T2: 事务 T1 首先锁定 表 A 的行 1。然后尝试锁定 表 B…...

符号秩检验
内容来源 非参数统计(第2版) 清华大学出版社 王星 褚挺进 编著 符号秩检验 在符号检验的基础上,增加了数据绝对值大小的信息 检验统计量 用一个简单的例子来说明 样本数据 X i , i 1 , ⋯ , 6 X_i,i1,\cdots,6 Xi,i1,⋯,6 如下 X …...

RainbowDash 的 Robot
H RainbowDash 的 Robot - 第七届校赛正式赛 —— 补题 题目大意: 给一个 n ∗ m n*m n∗m 的二维网格,在第 i i i 列中,前 a i a_i ai 单元格被阻断,无法通行,即 [ 1 , a i ] [1,a_i] [1,ai] 。 一个机器人正…...

yum repolist all全部禁用了 怎么办
文章目录 步骤思考解决yum仓库全部被禁用的问题步骤思考: 检查仓库状态:运行yum repolist all,查看所有仓库的启用状态。 被禁用的仓库会显示为disabled。 启用所有仓库:可以逐一启用,或者使用命令批量启用。 例如使用yum-config-manager --enable ‘*’,但需要注意是否有…...

SQL WHERE 与 HAVING
WHERE 和 HAVING 都是 SQL 中用于筛选数据的子句,但它们有重要的区别 WHERE 子句 在 分组前 过滤数据 作用于 原始数据行 不能使用聚合函数 执行效率通常比 HAVING 高 SELECT column1, column2 FROM table WHERE condition; HAVING 子句 在 分组后 过滤数据 …...

如何在 Unity3D 导入 Spine 动画
一、前言 《如何在 Unity3D 项目中导入 Spine 动画》,虽然在网上有很多这种文章,直接将问题交给 DeepSeek 也能得到具体的操作流程,但是照着他们提供的方法还是能遇到几个问题,比如: AI 回答没有提到 Unity 无法识别.…...

子网划分2
子网分配的问题,下列vlsm如何设置? 某公司申请了一个C类202.60.31.0的IP地址,要求设置三个子网,一个为100台主机,一个为50台主机,另一个为50台主机,用VLSM如何设置? 哪位高手指教一…...

C++的UDP连接解析域名地址错误
背景 使用c开发一个udp连接功能的脚本,可以接收发送数据,而且地址是经过内网穿透到外网的 经过 通常发送数据给目标地址,需要把目的地址结构化,要么使用inet_addr解析ip地址,要么使用inet_pton sockaddr_in target…...

23种设计模式中的观察者模式
定义了一种一对多的依赖关系,当一个对象的状态发生改变时,其所有依赖者都会收到通知并自动更新。 观察者模式是一种发布-订阅模式。它让发送通知的一方(被观察者)和接收通知的一方(观察者)能够解耦…...

论文笔记:ASTTN模型
研究现状 现有研究大多通过分别考虑空间相关性和时间相关性或在滑动时间窗口内对这种时空相关性进行建模,而未能对直接的时空相关性进行建模。受最近图领域Transformer成功的启发,该模型提出利用局部多头自关注,在自适应时空图上直接建立跨时…...

Java单例模式详解
单例模式详解 一、单例模式概述 单例模式(Singleton Pattern)是一种创建型设计模式,它确保一个类只有一个实例,并提供一个全局访问点来访问这个实例。 核心特点 唯一实例:保证一个类只有一个实例存在全局访问:提供统一的访问入…...

Linux命令-tar
tar 命令的完整参数列表: 参数 描述 -c 创建新的归档文件 -x 解压归档文件 -t 列出归档文件内容 -r 追加文件到归档文件 -u 更新归档文件中的文件 -d 从归档文件中删除文件 -f 指定归档文件的名称 -v 显示详细信息(verbose) -z 使用 gzip 压缩…...

深入解析 Git Submodule:从基础到高级操作指南
深入解析 Git Submodule:从基础到高级操作指南 一、Git Submodule 是什么? git submodule 是 Git 提供的一个强大功能,允许在一个 Git 仓库(主仓库)中嵌入另一个独立的 Git 仓库(子模块)。主仓…...

2025-4-2 蓝桥杯刷题情况(分布式队列)
1.题目描述 小蓝最近学习了一种神奇的队列:分布式队列。简单来说,分布式队列包含 N 个节点(编号为0至N-1,其中0号为主节点),其中只有一个主节点,其余为副节点。 主/副节点中都各自维护着一个队列,当往分布式队列中添加…...

C/C++指针核心难点全解析:从内存模型到实战避坑指南
引言:指针为何被称为C/C的“灵魂”? 指针是C/C语言中最强大的工具之一,也是开发者通往底层编程的必经之路。它直接操作内存地址的能力,赋予了程序极高的灵活性和性能优势。然而,指针的复杂性也让无数初学者“折戟沉沙…...
)
ray.rllib-入门实践-12-2:在自定义policy中注册使用自定义model(给自定义model新增参数)
建议先看博客 ray.rllib-入门实践-12-1:在自定义policy中注册使用自定义model , 本博客与之区别在于可以给自定义的 model 新增自定义的参数,并通过 config.model["custom_model_config"] 传入自定义的新增参数。 环境配置…...

【Java中级】10章、内部类、局部内部类、匿名内部类、成员内部类、静态内部类的基本语法和细节讲解配套例题巩固理解【5】
❤️ 【内部类】干货满满,本章内容有点难理解,需要明白类的实例化,学完本篇文章你会对内部类有个清晰的认知 💕 内容涉及内部类的介绍、局部内部类、匿名内部类(重点)、成员内部类、静态内部类 🌈 跟着B站一位老师学习…...
