数据结构优化DP总结
单调栈:Codeforces Round 622 (Div. 2) C2. Skyscrapers (hard version)

简单来讲就是最后需要呈现出一个单峰数组,使得总高度最高。
最开始想到暴力枚举每一个元素都充当最高的“单峰”,但是这里的 n 过大,这样枚举肯定会TLE。
那就考虑能不能单调线性的考虑每个元素作为最高点的时候的解是多少呢?
这里就需要借助我们的 单调栈,维护一个单调递增的序列:
- 这里仅以正序遍历为例:f[i]表示的是以i为单峰时1 — i 所有数组能产生的最大贡献,根据单调栈的性质,stk.top()就是上一个最近的小于 a[i] 的元素的下标,所以加上这中间所有的楼产生的贡献(由于单调栈的性质,这段中所有大于a[i] 的元素一定会被弹出,同时减去他们之前产生的贡献)。
#include<bits/stdc++.h>using namespace std;#define int long longsigned main() {int n, sum = 0;cin >> n;vector<int> a(n + 1);for (int i = 1; i <= n; i++) {cin >> a[i];}stack<int> stk;vector<int> f(n + 1, 0);sum = 0;for (int i = 1; i <= n; i++) {while(stk.size() && a[stk.top()] >= a[i]) {//先弹出所有大于a[i]的楼的下标,因为保证要单增int j = stk.top();stk.pop();sum -= (j - (stk.empty() ? 0 : stk.top())) * a[j];// 减去这些楼之前所产生的贡献}sum += (i - (stk.empty() ? 0 : stk.top())) * a[i]; //加上目前这栋楼所产生的贡献stk.push(i);f[i] += sum;}sum = 0;while(!stk.empty()) stk.pop(); for (int i = n; i >= 1; i--) {while(stk.size() && a[stk.top()] >= a[i]) {int j = stk.top();stk.pop();sum -= ((stk.empty() ? n + 1 : stk.top()) - j) * a[j];}sum += ((stk.empty() ? n + 1 : stk.top()) - i) * a[i];stk.push(i);f[i] += sum - a[i];}auto p = max_element(f.begin() + 1, f.end()) - f.begin();//cout << p << endl;for (int i = p - 1; i >= 1; i--) {a[i] = min(a[i], a[i + 1]);}for (int i = p + 1; i <= n; i++) {a[i] = min(a[i], a[i - 1]);}for (int i = 1; i <= n; i++) {cout << a[i] << " \n"[i == n];}return 0;
}
建议先熟练掌握单调栈再来理解这题。
树状数组:Codeforces Round 1013 (Div. 3) F. Igor and Mountain

其实也不一定需要树状数组,用前缀和也能达到一样的效果,只是树状数组比较好写,不费脑子。
简单来说就是如果暴力枚举转移的话会超时,所以就需要记录下整个区间的某种贡献,然后一起转移,这样就可以省下很多的时间。
i64 mod = 998244353;double get_dist(int a, int b, int c, int d) {double dx = fabs(a - c);double dy = fabs(b - d);return sqrt(dx * dx + dy * dy);
}template <typename T>
class Fenwick {
public:int n;std::vector<T> a;Fenwick(int n_ = 0) {init(n_);}void init(int n_) {n = n_;a.assign(n + 1, T{});}void add(int x, const T &v) {for (int i = x; i <= n; i += i & -i) {a[i] = (a[i] + v % mod + mod) % mod;}}// 查询位置 [1, x] 的前缀和T sum(int x) {T ans{};for (int i = x; i > 0; i -= i & -i) {ans = (ans + a[i] % mod + mod) % mod;}return ans;}// 查询区间 [l, r] 的区间和T rangeSum(int l, int r) {return (sum(r) - sum(l - 1) + mod) % mod;}int select(const T &k) {int x = 0;T cur{};for (int i = 1 << std::__lg(n); i; i /= 2) {if (x + i <= n && cur + a[x + i] <= k) {x += i;cur = cur + a[x];}}return x;}
};void solve()
{int n, m, d1, d2;cin >> n >> m >> d1;for (int i = 0; i <= d1; i++) {if(i * i + 1 <= d1 * d1) {d2 = i;}}vector<string> g(n + 1);for (int i = 1; i <= n; i++) {cin >> g[i];g[i] = ' ' + g[i];}int ans = 0;vector<Fenwick<int>> f(n + 1, Fenwick<int>(m + 1)), nf(f);for (int j = 1; j <= m; j++) {if (g[n][j] == 'X') {f[n].add(j, 1);}}for (int j = 1; j <= m; j++) {if (g[n][j] == 'X') {nf[n].add(j, f[n].rangeSum(max(1LL, j - d1), min(j + d1, m)));}}// for (int j = 1; j <= m; j++) {// cout << nf[n].rangeSum(j, j) << ' ';// }// cout << endl;for (int i = n - 1; i >= 1; i--) {for (int j = 1; j <= m; j++) {if (g[i][j] == 'X') {f[i].add(j, nf[i + 1].rangeSum(max(1LL, j - d2), min(j + d2, m)));}}for (int j = 1; j <= m; j++) {if (g[i][j] == 'X') {nf[i].add(j, f[i].rangeSum(max(1LL, j - d1), min(j + d1, m)));}}}ans = nf[1].sum(m);cout << (ans + mod) % mod << endl;
}相关文章:

数据结构优化DP总结
单调栈:Codeforces Round 622 (Div. 2) C2. Skyscrapers (hard version) 简单来讲就是最后需要呈现出一个单峰数组,使得总高度最高。 最开始想到暴力枚举每一个元素都充当最高的“单峰”,但是这里的 n 过大,这样枚举肯定会TLE。 …...

[Linux系统编程]进程间通信—system V
进程间通信—system V 1. System V 共享内存(Shared Memory)1.1 共享内存的建立过程1.2 共享内存函数2. System V 消息队列(Message Queues)3. System V 信号量(Semaphores)4. 总结前言: 之前所提的管道通信是基于文件的,OS没有做过多的设计工作。 system V 进程间通信…...

Eigen库几何模块深度解析与实践指南
Eigen库几何模块深度解析与实践指南 a. Eigen几何模块概述 i. 几何模块的核心功能 在三维空间中,几何变换是描述物体位置和姿态变化的基础,其数学基础涵盖了线性代数中的矩阵运算等知识。Eigen库的几何模块为这些变换提供了高效且便捷的实现方式。 旋转、平移和缩放是三维…...

第十四届蓝桥杯大赛软件赛省赛C/C++ 大学 B 组(部分题解)
文章目录 前言日期统计题意: 冶炼金属题意: 岛屿个数题意: 子串简写题意: 整数删除题意: 总结 前言 一年一度的🏀杯马上就要开始了,为了取得更好的成绩,好名字写了下前年2023年蓝桥…...

C语言常见3种排序
主要是三种排序方法:冒泡排序、选择排序、插入排序。 文章目录 一、冒泡排序 1.代码: 2.工作原理: 3.具体过程: 二、选择排序 1.代码 2. 工作原理 3.具体过程: 三、插入排序 1.代码 2.工作原理 3.具体过程 总结 一、…...
分析sys高问题的方法总结
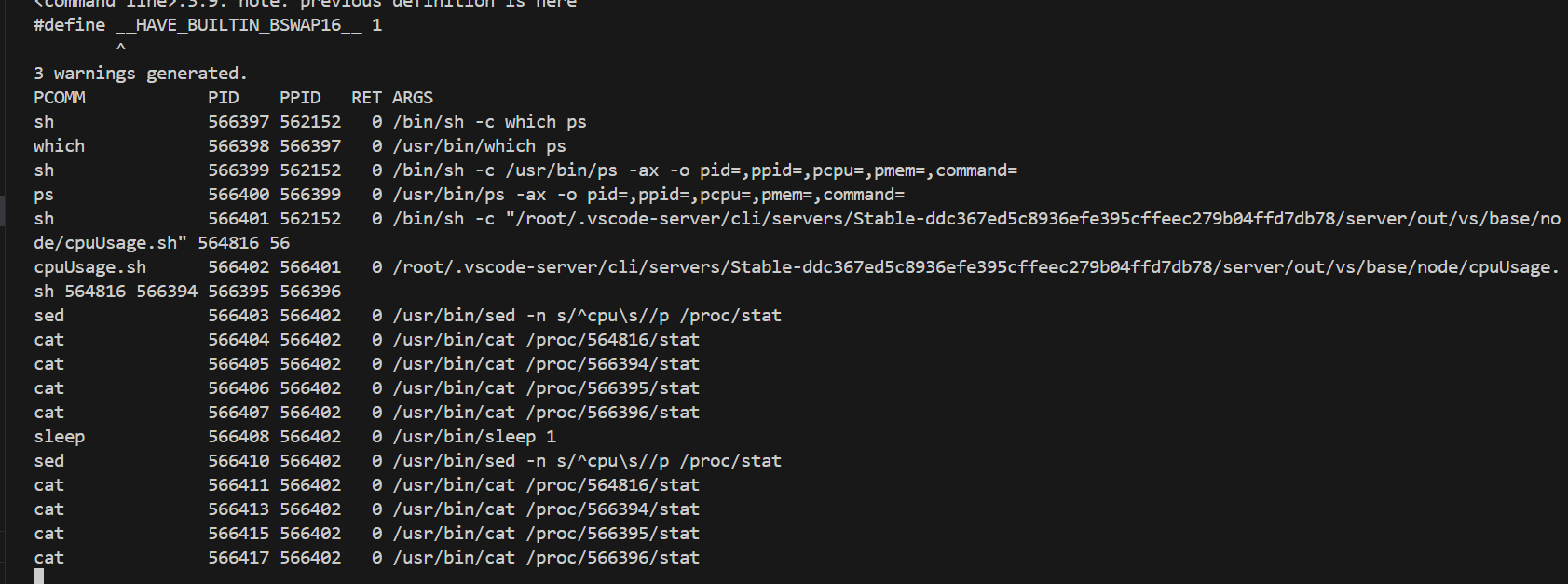
一、背景 sys高的问题往往属于底层同学更需要关注的问题,sys高的问题往往表现为几种情况,一种是瞬间的彪高,一种是持续的彪高。这篇博客里,我们总结一下常用的分析方法和分析工具的使用来排查这类sys高的问题。 二、通过mpstat配…...

智谱发布AI Agent“AutoGLM沉思”,开启AI“边想边干”新时代
近日,智谱正式推出全新AI Agent产品——AutoGLM沉思,标志着人工智能从“思考”迈向“执行”的关键突破。该智能体不仅具备深度研究能力,还能自主完成实际操作,真正实现“边想边干”的智能化应用。 在演示环节,智谱展示…...

使用Leaflet对的SpringBoot天地图路径规划可视化实践-以黄花机场到橘子洲景区为例
目录 前言 一、路径规划需求 1、需求背景 2、技术选型 3、功能简述 二、Leaflet前端可视化 1、内容布局 2、路线展示 3、转折路线展示 三、总结 前言 在当今数字化与智能化快速发展的时代,路径规划技术已经成为现代交通管理、旅游服务以及城市规划等领域的…...

【小兔鲜】day02 Pinia、项目起步、Layout
【小兔鲜】day02 Pinia、项目起步、Layout 1. Pinia2. 添加Pinia到Vue项目3. 案例:Pinia-counter基础使用3.1 Store 是什么?3.2 应该在什么时候使用 Store? 4. Pinia-getters和异步action4.1 getters4.2 action如何实现异步 1. Pinia Pinia 是 Vue 的专…...

PyTorch 激活函数
激活函数是神经网络中至关重要的组成部分,它们为网络引入了非线性特性,使得神经网络能够学习复杂模式。PyTorch 提供了多种常用的激活函数实现。 常用激活函数 1. ReLU (Rectified Linear Unit) 数学表达式: PyTorch实现: torch.nn.ReLU(inplaceFals…...

魔塔社区使用llamafactory微调AI阅卷试题系统
启动 LLaMA-Factory 1. 安装 LLaMA-Factory 执行安装指令 git clone --depth 1 https://github.com/hiyouga/LLaMA-Factory.git cd LLaMA-Factory pip install -e ".[torch,metrics]"解决依赖冲突 如果遇到依赖冲突,可使用以下命令安装,不…...

Java面试黄金宝典29
1. 什么是普通索引和唯一性索引 定义: 普通索引:是最基本的索引类型,它为数据表中的某一列或多列建立索引,以加快数据的查询速度。它不限制索引列的值重复,允许存在多个相同的值。唯一性索引:在普通索引的基…...

git `switch` 命令详解与实用示例
文章目录 git switch 命令详解与实用示例git switch vs git checkoutgit switch 用法1. 切换到已有分支2. 创建并切换到新分支3. 切换到上一个分支4. 切换到远程分支(自动创建本地分支并追踪远程)5. 放弃未提交的修改并切换分支 总结 git switch 命令详解…...

Oracle中文一二三四排序【失败】
原文地址: Oracle数据库如何对中文的一二三四五六七八九十数进行正序排列排序_中文数字排序-CSDN博客 自定义排序函数 -- 自定义中文映射阿拉伯数字函数 CREATE OR REPLACE FUNCTION P_ORDER_CHINESE_TO_ARABIC(V_NUM VARCHAR2) RETURN NUMBER IS BEGIN-- 根据…...

AWS S3 和 Lambda 使用
目录: AWS概述 EMR Serverless AWS VPC及其网络 关于AWS网络架构的思考 AWS S3 和 Lambda 使用 本文将通过一个实例来说明如何使用 AWS S3 和 Lambda。 使用场景:通过代码将文件上传到S3,该文件需要是公开访问的,并对上传的文件进…...

Mysql 在什么样的情况下会产生死锁?
在 MySQL 中,死锁是指两个或多个事务相互等待对方释放锁,导致所有相关事务无法继续执行的情况。死锁会影响数据库的并发性能,因此需要及时检测并处理。假设有两个事务 T1 和 T2: 事务 T1 首先锁定 表 A 的行 1。然后尝试锁定 表 B…...

符号秩检验
内容来源 非参数统计(第2版) 清华大学出版社 王星 褚挺进 编著 符号秩检验 在符号检验的基础上,增加了数据绝对值大小的信息 检验统计量 用一个简单的例子来说明 样本数据 X i , i 1 , ⋯ , 6 X_i,i1,\cdots,6 Xi,i1,⋯,6 如下 X …...

RainbowDash 的 Robot
H RainbowDash 的 Robot - 第七届校赛正式赛 —— 补题 题目大意: 给一个 n ∗ m n*m n∗m 的二维网格,在第 i i i 列中,前 a i a_i ai 单元格被阻断,无法通行,即 [ 1 , a i ] [1,a_i] [1,ai] 。 一个机器人正…...

yum repolist all全部禁用了 怎么办
文章目录 步骤思考解决yum仓库全部被禁用的问题步骤思考: 检查仓库状态:运行yum repolist all,查看所有仓库的启用状态。 被禁用的仓库会显示为disabled。 启用所有仓库:可以逐一启用,或者使用命令批量启用。 例如使用yum-config-manager --enable ‘*’,但需要注意是否有…...

SQL WHERE 与 HAVING
WHERE 和 HAVING 都是 SQL 中用于筛选数据的子句,但它们有重要的区别 WHERE 子句 在 分组前 过滤数据 作用于 原始数据行 不能使用聚合函数 执行效率通常比 HAVING 高 SELECT column1, column2 FROM table WHERE condition; HAVING 子句 在 分组后 过滤数据 …...

如何在 Unity3D 导入 Spine 动画
一、前言 《如何在 Unity3D 项目中导入 Spine 动画》,虽然在网上有很多这种文章,直接将问题交给 DeepSeek 也能得到具体的操作流程,但是照着他们提供的方法还是能遇到几个问题,比如: AI 回答没有提到 Unity 无法识别.…...

子网划分2
子网分配的问题,下列vlsm如何设置? 某公司申请了一个C类202.60.31.0的IP地址,要求设置三个子网,一个为100台主机,一个为50台主机,另一个为50台主机,用VLSM如何设置? 哪位高手指教一…...

C++的UDP连接解析域名地址错误
背景 使用c开发一个udp连接功能的脚本,可以接收发送数据,而且地址是经过内网穿透到外网的 经过 通常发送数据给目标地址,需要把目的地址结构化,要么使用inet_addr解析ip地址,要么使用inet_pton sockaddr_in target…...

23种设计模式中的观察者模式
定义了一种一对多的依赖关系,当一个对象的状态发生改变时,其所有依赖者都会收到通知并自动更新。 观察者模式是一种发布-订阅模式。它让发送通知的一方(被观察者)和接收通知的一方(观察者)能够解耦…...

论文笔记:ASTTN模型
研究现状 现有研究大多通过分别考虑空间相关性和时间相关性或在滑动时间窗口内对这种时空相关性进行建模,而未能对直接的时空相关性进行建模。受最近图领域Transformer成功的启发,该模型提出利用局部多头自关注,在自适应时空图上直接建立跨时…...

Java单例模式详解
单例模式详解 一、单例模式概述 单例模式(Singleton Pattern)是一种创建型设计模式,它确保一个类只有一个实例,并提供一个全局访问点来访问这个实例。 核心特点 唯一实例:保证一个类只有一个实例存在全局访问:提供统一的访问入…...

Linux命令-tar
tar 命令的完整参数列表: 参数 描述 -c 创建新的归档文件 -x 解压归档文件 -t 列出归档文件内容 -r 追加文件到归档文件 -u 更新归档文件中的文件 -d 从归档文件中删除文件 -f 指定归档文件的名称 -v 显示详细信息(verbose) -z 使用 gzip 压缩…...

深入解析 Git Submodule:从基础到高级操作指南
深入解析 Git Submodule:从基础到高级操作指南 一、Git Submodule 是什么? git submodule 是 Git 提供的一个强大功能,允许在一个 Git 仓库(主仓库)中嵌入另一个独立的 Git 仓库(子模块)。主仓…...

2025-4-2 蓝桥杯刷题情况(分布式队列)
1.题目描述 小蓝最近学习了一种神奇的队列:分布式队列。简单来说,分布式队列包含 N 个节点(编号为0至N-1,其中0号为主节点),其中只有一个主节点,其余为副节点。 主/副节点中都各自维护着一个队列,当往分布式队列中添加…...

C/C++指针核心难点全解析:从内存模型到实战避坑指南
引言:指针为何被称为C/C的“灵魂”? 指针是C/C语言中最强大的工具之一,也是开发者通往底层编程的必经之路。它直接操作内存地址的能力,赋予了程序极高的灵活性和性能优势。然而,指针的复杂性也让无数初学者“折戟沉沙…...
