蓝桥杯——走迷宫问题(BFS)
这是一个经典的BFS算法

1. BFS算法保证最短路径
- 核心机制:广度优先搜索按层遍历所有可能的路径,首次到达终点的路径长度即为最短步数。这是BFS的核心优势。
- 队列的作用:通过队列按先进先出的顺序处理节点,确保每一步探索的都是当前层所有可能的节点,不会跳过更短的路径。
2. 坐标与地图的映射
- 地图存储:使用二维数组
map存储迷宫,其中每个元素的值表示该位置是否可通行(如0为可通行,1为障碍物)。 - 坐标处理:你的代码假设输入的起点和终点坐标是 1-based(即从1开始),但在数组中直接以 0-based 索引访问,未做转换。这可能导致越界或定位错误(需修正)。
3. 步数记录与状态管理
- 步数数组
dp:记录从起点到每个坐标的最小步数。初始化时起点步数为0(但你的代码中未显式初始化,可能导致逻辑错误)。 - 访问标记:通过
dp[nextx][nexty] == 0判断节点是否被访问过,避免重复计算。
4. 移动规则与边界检查
- 四个方向移动:通过
dx和dy数组定义右、下、左、上四个方向的坐标变化。 - 边界条件:检查坐标是否在
[0, n)和[0, m)范围内,防止数组越界。 - 障碍物判断:你的代码中允许移动到
map[nextx][nexty] != 0的区域,但通常逻辑应为map[nextx][nexty] == 0表示可通行(此处存在逻辑错误)。
5. 终止条件
- 终点判断:当前节点坐标等于终点坐标时,直接输出步数并返回。
- 无解处理:队列清空后仍未到达终点,输出
-1表示无解。
代码如下
import java.util.*;
import java.util.concurrent.LinkedBlockingDeque;
// 1:无需package
// 2: 类名必须Main, 不可修改public class Main {public static class node {int x;int y;public node(int x, int y) {this.x = x;this.y = y;}}public static void main(String[] args) {// 创造点对象,方便数据操作// 创建一个数组用来记录地图,地图为nxm,// 我们将之后的地图边界设置为1,防止索引越界,地图边界为1-n,1-m,// 创建一个数组记录该位置累计的最小的步数// 创建一个需要拓展点的队列// 这个队列是很有必要的,若是这个队列里面有值,就代表可以拓展,就可以避免走不出去的情况// 开始向四个方向的路走,要判断这个方向的路是否可走(边界、障碍物)、// 如果可走就将该点存入队列,确保队列还有值,还能继续在迷宫里走// 终止条件,是否到达终点,到终点就将值传进去//基础传值操作Scanner scan = new Scanner(System.in);int n = scan.nextInt();int m = scan.nextInt();int[][] map = new int[n][m];for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {map[i][j] = scan.nextInt();}}int startx = scan.nextInt();int starty = scan.nextInt();int endx = scan.nextInt();int endy = scan.nextInt();//这里有一个混淆点,题目给我们的坐标(1,1) (5,5)但对应在数组上的索引应该是[0,0] [4,4]node start = new node(startx-1, starty-1);node end = new node(endx-1, endy-1);//只需要一张地图和起点,终点BFS(map, start, end);scan.close();}public static void BFS(int[][] map, node start, node end) {//数据初始化int n = map.length;int m = map[0].length;int[] dx = {0, 1, 0, -1};int[] dy = {1, 0, -1, 0};int[][] dp = new int[n][m];
// Arrays.stream(dp).forEach(ints -> Arrays.fill(ints, -1));// if (map[start.x][start.y] == 1) {
// System.out.println(-1);
// return;
// }//初始化队列将起点放进去0Queue<node> queue = new LinkedBlockingDeque<>();queue.add(start);//只要队列不为空就可以一直走while (!queue.isEmpty()) {node now = queue.poll();//从队列里面取值,取完值就得将该值删除//当前节点等于终点直接输出结果if (now.x == end.x && now.y == end.y) {System.out.println(dp[now.x][now.y]);return;}int nowx = now.x;int nowy = now.y;for (int i = 0; i < 4; i++) {int nextx = nowx + dx[i];int nexty = nowy + dy[i];node next = new node(nextx, nexty);//边界判断 x[0,n) y[0,m) ,还有地图不能等于1,并且这个地方没被走过if ((nextx >= 0 && nextx < n) &&(nexty >= 0 && nexty < m) &&(map[nextx][nexty] != 0) &&(dp[nextx][nexty] == 0)) {queue.add(next);//下一步可走就将该点加入队列,假如若有四次可走就将这四个点都加入队列,//之后就可以从这队列里面取可走的点然后继续拓展可走的点的四个方向dp[nextx][nexty] = dp[nowx][nowy] + 1;//走过的地方步数都大于1}}}//无法到达终点System.out.println(-1);}}
这里有一个混淆点,由于他题目给的坐标和索引不对应导致卡了半天没想到居然还能过71.4%

相关文章:

蓝桥杯——走迷宫问题(BFS)
这是一个经典的BFS算法 1. BFS算法保证最短路径 核心机制:广度优先搜索按层遍历所有可能的路径,首次到达终点的路径长度即为最短步数。这是BFS的核心优势。队列的作用:通过队列按先进先出的顺序处理节点,确保每一步探索的都是当…...

详解 Redis repl_backlog_buffer(如何判断增量同步)
一、repl_backlog_buffer 复制积压缓冲区(Replication Backlog Buffer) 是一个环形内存区域(Ring Buffer),用于临时保存主节点最近写入的写命令,以支持从节点断线重连后的增量同步。 1.1 三个复制偏移量 …...

服务器虚拟化技术深度解析:医药流通行业IT架构优化指南
一、服务器虚拟化的定义与原理 (一)技术定义:从物理到虚拟的资源重构 服务器虚拟化是通过软件层(Hypervisor)将物理服务器的CPU、内存、存储、网络等硬件资源抽象为逻辑资源池,分割成多个相互隔离的虚拟机…...

使用PyTorch实现ResNet:从残差块到完整模型训练
ResNet(残差网络)是深度学习中的经典模型,通过引入残差连接解决了深层网络训练中的梯度消失问题。本文将从残差块的定义开始,逐步实现一个ResNet模型,并在Fashion MNIST数据集上进行训练和测试。 1. 残差块(…...

Scala相关知识学习总结5
1、多维数组 定义: val arr Array.ofDim[Double](3,4) 表示二维数组中有三个一维数组,每个一维数组有四个元素。 2、列表 List 不可变 List:默认不可变,可创建有序且可重复的列表,可使用:从右向左增加数据…...

Day1:前端项目uni-app壁纸实战
uni-app官网下载HBuilder。 uni-app快速上手 | uni-app官网 点击HBuilder 安装 新建项目 工具——插件安装 安装uni-app(vue3) 我们先来准备一下: 先在wallpaper下新建目录 我已经建过了 同样,再在common下建images和style目录&…...

光谱相机的光谱数据采集原理
光谱相机的光谱数据采集原理基于分光技术和光电信号转换,通过将入射光按波长分解并记录各波段的强度信息,最终生成包含空间和光谱维度的数据立方体。以下是详细原理分解: 1. 分光技术:将复合光分解为单色光 光谱相机…...

《算法笔记》10.3小节——图算法专题->图的遍历 问题 A: 第一题
题目描述 该题的目的是要你统计图的连通分支数。 输入 每个输入文件包含若干行,每行两个整数i,j,表示节点i和j之间存在一条边。 输出 输出每个图的联通分支数。 样例输入 1 4 4 3 5 5样例输出 2 分析: 由于题目没给出范围࿰…...

python中的{}
注意,如果要创建空集合,只能使用 set() 函数实现。因为直接使用一对 {},Python 解释器会将其视为一个空字典。 Python中集合set和字典dict的用法区别_python创建set变量和dict区别-CSDN博客...
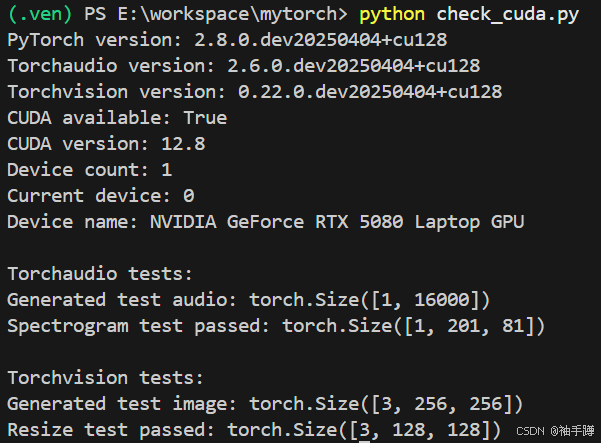
宏碁笔记本电脑擎7PRO搭载的 NVIDIA RTX 5080 显卡安装pytorch
宏碁笔记本电脑擎7PRO搭载的 NVIDIA RTX 5080 显卡是一款高性能移动 GPU,基于 NVIDIA 最新的 Blackwell 架构设计,通过修正架构(Blackwell)、显存类型与带宽(GDDR7、960GB/s)、Tensor Core 与 RT Core 全面…...

html+css+js 实现一个贪吃蛇小游戏
目录 游戏简介 游戏功能与特点 如何玩转贪吃蛇 游戏设计与实现 HTML结构 JavaScript核心实现 代码结构: 效果 关于“其他游戏” 游戏简介 贪吃蛇是一款经典的单人小游戏,玩家通过控制蛇的移动,吃掉食物来增加长度,避免撞…...
API接口解析)
淘宝按图搜索商品(拍立淘)API接口解析
以下是关于淘宝按图搜索商品(拍立淘)API的深度解析指南,结合官方文档和开发者经验整理,包含调用方法、参数详解、返回结果解析及常见问题处理: 一、API核心接口说明 1. 接口名称 官方接口:taobao.image.…...

Python爬虫生成CSV文件的完整流程
引言 在当今数据驱动的时代,网络爬虫已成为获取互联网数据的重要工具。Python凭借其丰富的库生态系统和简洁的语法,成为了爬虫开发的首选语言。本文将详细介绍使用Python爬虫从网页抓取数据并生成CSV文件的完整流程,包括环境准备、网页请求、…...

21.OpenCV获取图像轮廓信息
OpenCV获取图像轮廓信息 在计算机视觉领域,识别和分析图像中的对象形状是一项基本任务。OpenCV 库提供了一个强大的工具——轮廓检测(Contour Detection),它能够帮助我们精确地定位对象的边界。这篇博文将带你入门 OpenCV 的轮廓…...

医学图像分割效率大幅提升!U-Net架构升级,助力精度提升5%!
在医学图像分割领域,U-Net模型及其变体的创新应用正在带来显著的性能提升和效率优化。最新研究显示,通过引入结构化状态空间模型(SSM)和轻量级LSTM(xLSTM)等技术,VMAXL-UNet模型在多个医学图像数…...

智能设备运行监控系统
在工业 4.0 与智能制造浪潮下,设备运行效率与稳定性成为企业竞争力的核心要素。然而,传统设备管理模式面临数据采集分散、状态分析滞后、维护成本高昂等痛点。为破解这些难题,设备运行监控系统应运而生,通过融合智能传感、5G 通信…...

详细分析单例模式
目录 1.单例模式的定义 2.单例模式的实现方式 1.饿汉模式 2.懒汉模式 (1)线程不安全的问题怎么解决? (2)直接对整个getInstance方法代码块加锁吗? (3)那对if语句加锁不就行了吗…...

Windwos的DNS解析命令nslookup
nslookup 解析dns的命令 有两种使用方式,交互式&命令行方式。 交互式 C:\Users\Administrator>nslookup 默认服务器: UnKnown Address: fe80::52f7:edff:fe28:35de> www.baidu.com 服务器: UnKnown Address: fe80::52f7:edff:fe28:35de非权威应答:…...

服务器报错:xxx/libc.so.6: version `GLIBC_2.32‘ not found
/lib/x86_64-linux-gnu/libc.so.6: version GLIBC_2.32 not found (required by ./aima-sim-app-main) 解决思路 根据错误信息,您的应用程序 aima-sim-app-main 和 libmujoco.so.3.1.6 库依赖于较新的 GNU C Library (glibc) 版本(如 GLIBC_2.32, GLIBC…...

Flutter之页面布局一
目录: 1、页面布局一2、无状态组件StatelessWidget和有状态组件StatefulWidget2.1、无状态组件示例2.2、有状态组件示例2.3、在 widget 之间共享状态1、使用 widget 构造函数2、使用 InheritedWidget3、使用回调 3、布局小组件3.1、布置单个 Widget3.2、容器3.3、垂…...

架构思维: 数据一致性的两种场景深度解读
文章目录 Pre案例数据一致性问题的两种场景第一种场景:实时数据不一致不要紧,保证数据最终一致性就行第二种场景:必须保证实时一致性 最终一致性方案实时一致性方案TCC 模式Seata 中 AT 模式的自动回滚一阶段二阶段-回滚二阶段-提交 Pre 架构…...

大数据knox网关API
我们过去访问大数据组件,如sparkui,hdfs的页面,以及yarn上面看信息是很麻烦的一件事。要记每个端口号,比如50070,8090,8088,4007,如果换到另一个集群,不同版本࿰…...
)
UI测试(2)
1、HTML 是用来描述网页的一种语言。 指的是超文本标记语言 (Hyper Text Markup Language) ,HTML 不是一种编程语言,而是一种标记语言 (markup language) 负责定义页面呈现的内容:标签语言:<标签名>标签值<标签名>&am…...

【Tauri2】015——前端的事件、方法和invoke函数
目录 前言 正文 准备 关键url 获取所有命令 切换主题set_theme 设置大小 获得版本version 名字name 监听窗口移动 前言 【Tauri2】005——tauri::command属性与invoke函数-CSDN博客https://blog.csdn.net/qq_63401240/article/details/146581991?spm1001.2014.3001.…...

密码学基础——分组密码的运行模式
前面的文章中文我们已经知道了分组密码是一种对称密钥密码体制,其工作原理可以概括为将明文消息分割成固定长度的分组,然后对每个分组分别进行加密处理。 下面介绍分组密码的运行模式 1.电码本模式(ECB) 2.密码分组链接模式&…...

Android SELinux权限使用
Android SELinux权限使用 一、SELinux开关 adb在线修改seLinux(也可以改配置文件彻底关闭) $ getenforce; //获取当前seLinux状态,Enforcing(表示已打开),Permissive(表示已关闭) $ setenforce 1; //打开seLinux $ setenforce 0; //关闭seLinux二、命令查看sel…...

Python----计算机视觉处理(Opencv:道路检测完整版:透视变换,提取车道线,车道线拟合,车道线显示,)
Python----计算机视觉处理(Opencv:道路检测之道路透视变换) Python----计算机视觉处理(Opencv:道路检测之提取车道线) Python----计算机视觉处理(Opencv:道路检测之车道线拟合) Python----计算机视觉处理࿰…...

基于飞桨框架3.0本地DeepSeek-R1蒸馏版部署实战
深度学习框架与大模型技术的融合正推动人工智能应用的新一轮变革。百度飞桨(PaddlePaddle)作为国内首个自主研发、开源开放的深度学习平台,近期推出的3.0版本针对大模型时代的开发痛点进行了系统性革新。其核心创新包括“动静统一自动并行”&…...

docker初始环境搭建(docker、Docker Compose、portainer)
docker、Docker Compose和portainer的安装部署、使用 docker、Docker Compose和portainer的安装部署、使用一.安装docker1.失败的做法2.首先卸载旧版本(没安装则下一步)3.配置下载的yum来源,不然yum search搜不到4.安装启动docker5.替换国内源…...

开源RuoYi AI助手平台的未来趋势
近年来,人工智能技术的迅猛发展已经深刻地改变了我们的生活和工作方式。 无论是海外的GPT、Claude等国际知名AI助手,还是国内的DeepSeek、Kimi、Qwen等本土化解决方案,都为用户提供了前所未有的便利。然而,对于那些希望构建属于自…...
