【数据结构】树的介绍
目录
- 一、树
- 1.1什么是树?
- 1.2 树的概念与结构
- 1.3树的相关术语
- 1.4 树形结构实际运用场景
- 二、二叉树
- 2.1 概念与结构
- 2.2 特殊的二叉树
- 2.2.1 满二叉树
- 2.2.2 完全二叉树
个人主页,点击这里~
数据结构专栏,点击这里~

一、树
1.1什么是树?
这是我们生活中常见的树:

(以上图片来自网络,如若侵权联系自删)
生活中许多东西都可以抽象成为一棵树,例如一本书的目录:

它们都像自然界中的树一样,从根衍生出许多枝干,再由枝干衍生出许多更小的枝干,最终衍生出了许多叶子。
1.2 树的概念与结构
树是⼀种非线性的数据结构,它是由n(n>=0)个有限结点组成⼀个具有层次关系的集合。把它叫做树是因为它看起来像⼀棵倒挂的树,也就是说它是根朝上,而叶朝下的。
- 有⼀个特殊的结点,称为根结点,根结点没有前驱结点。
- 除根结点外,其余结点被分成
M(M>0)个互不相交的集合T1、T2、……、Tm,其中每⼀个集合Ti(1 <= i <= m)又是⼀棵结构与树类似的子树。每棵子树的根结点有且只有⼀个前驱,可以有 0 个或多个后继。因此,树是递归定义的。
注意:树形结构中,子树之间不能有交集,否则就不是树形结构。

非树形结构:

关于树:
- 子树是不相交的(如果存在相交就是图了);
- 除了根结点外,每个结点有且仅有⼀个父结点;
- ⼀棵
N个结点的树有N-1条边!
1.3树的相关术语

父结点/双亲结点:若⼀个结点含有子结点,则这个结点称为其子结点的父结点;如上图:A是B的父结点。
子结点/孩子结点:⼀个结点含有的子树的根结点称为该结点的子结点; 如上图:B是A的孩子结点。
结点的度:⼀个结点有几个孩子,它的度就是多少;比如A的度为6,F的度为2,K的度为0。
树的度:⼀棵树中,最大的结点的度称为树的度; 如上图:树的度为 6。
叶子结点/终端结点:度为 0 的结点称为叶结点; 如上图:B、C、H、I...等结点为叶结点。
分支结点/非终端结点:度不为0的结点; 如上图:D、E、F、G...等结点为分支结点。
兄弟结点:具有相同父结点的结点互称为兄弟结点(亲兄弟); 如上图:B、C 是兄弟结点。
结点的层次:从根开始定义起,根为第 1 层,根的子结点为第 2 层,以此类推;
树的高度或深度:树中结点的最大层次; 如上图:树的高度为 4。
结点的祖先:从根到该结点所经分支上的所有结点;如上图: A 是所有结点的祖先。
路径:⼀条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列;比如A到Q的路径为:A-E-J-Q;H到Q的路径H-D-A-E-J-Q。
子孙:以某结点为根的子树中任⼀结点都称为该结点的子孙。如上图:所有结点都是A的子孙。
森林:由 m(m>0) 棵互不相交的树的集合称为森林;
1.4 树形结构实际运用场景
文件系统是计算机存储和管理文件的⼀种方式,它利用树形结构来组织和管理文件和文件夹。在文件系统中,树结构被⼴泛应⽤,它通过父结点和子结点之间的关系来表示不同层级的文件和文件夹之间的关联。

二、二叉树
2.1 概念与结构
在树形结构中,我们最常用的就是二叉树,⼀棵二叉树是结点的⼀个有限集合,该集合由⼀个根结点加上两棵别称为左子树和右子树的二叉树组成,或者为空。
 从上图可以看出二叉树具备以下特点:
从上图可以看出二叉树具备以下特点:
- 二叉树不存在度大于
2的结点。 - 二叉树的子树有左右之分,次序不能颠倒,因此⼆叉树是有序树。
注意:对于任意的二叉树都是由以下几种情况复合而成的:

自然界的二叉树:

(以上图片来自网络,如若侵权联系自删)
2.2 特殊的二叉树
2.2.1 满二叉树
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果⼀个二叉树的层数为 K ,且结点总数是 2k − 1,则它就是满二叉树。

2.2.2 完全二叉树
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为 K 的,有 n 个结点的二叉树,当且仅当其每⼀个结点都与深度为K的满二叉树中编号从 1 ⾄n 的结点⼀⼀对应时称之为完全二叉树。要注意的是满二叉树是⼀种特殊的完全二叉树。

注意:这里如果J是E的右孩子树,那就不是一一对应的关系了,那这棵树就不是完全二叉树。
特点:
- 除了最后一层,每层结点个数达到最大。
- 最后一层结点个数不一定达到最大。
- 结点从左到右依次排列。
二叉树的性质:
- 若规定根结点的层数为 1 ,则⼀棵非空二叉树的第i层上最多有 2i−1 个结点。
- 若规定根结点的层数为 1 ,则深度为 h 的二叉树的最大结点数是 2h − 1。
- 若规定根结点的层数为 1 ,具有 n 个结点的满二叉树的深度 h = log(2) (n + 1) 。( log以2为底, n+1 为对数)。
总结:
以上就是本期博客分享的全部内容啦!如果觉得文章还不错的话可以三连支持一下,你的支持就是我前进最大的动力!
技术的探索永无止境! 道阻且长,行则将至!后续我会给大家带来更多优质博客内容,欢迎关注我的CSDN账号,我们一同成长!
(~ ̄▽ ̄)~
相关文章:

【数据结构】树的介绍
目录 一、树1.1什么是树?1.2 树的概念与结构1.3树的相关术语1.4 树形结构实际运用场景 二、二叉树2.1 概念与结构2.2 特殊的二叉树2.2.1 满二叉树2.2.2 完全二叉树 个人主页,点击这里~ 数据结构专栏,点击这里~ 一、树 1.1什么是树࿱…...

大模型是如何把向量解码成文字输出的
hidden state 向量 当我们把一句话输入模型后,例如 “Hello world”: token IDs: [15496, 995]经过 Embedding Transformer 层后,会得到每个 token 的中间表示,形状为: hidden_states: (batch_size, seq_len, hidd…...

Android源码之App启动
目录 App启动概述 App启动过程 App启动过程图 源码概述 跨进程启动 进程内启动 下面以应用桌面Launcher启动App的MainActivity来举例: App启动概述 首先,MainActivity是由Launcher组件来启动的,而Launcher又是通过Activity管理服务Act…...

nginx如何实现负载均衡?
Nginx 是一款高性能的 Web 服务器和反向代理服务器,它可以通过配置实现负载均衡功能。以下是实现负载均衡的详细步骤和方法: 1. 基本概念 负载均衡是将客户端请求分发到多个后端服务器上,以提高系统的可用性和性能。Nginx 支持多种负载均衡策…...
【GESP】C++二级练习 luogu-B3721 [语言月赛202303] Stone Gambling S
GESP二级练习,多层循环分支练习,难度★✮☆☆☆。 题目题解详见:https://www.coderli.com/gesp-2-luogu-b3721/ 【GESP】C二级练习 luogu-B3721 [语言月赛202303] Stone Gambling S | OneCoderGESP二级练习,多层循环分支练习&am…...

2. Qt界面文件原理
本节主要介绍ui文件如何与窗口关联,并通过隐式连接方式显示对话框 本文部分ppt、视频截图原链接:[萌马工作室的个人空间-萌马工作室个人主页-哔哩哔哩视频] 1 UI文件如何与窗口关联 1.1 mainwindow.cpp的头文件ui_mainwindow.h 根据编译原理的基本规…...

Elastic 的 OpenTelemetry 分发版(EDOT)现已正式发布:开源、可用于生产环境的 OTel
作者:来自 Elastic Miguel Luna 及 Bahubali Shetti Elastic 自豪地宣布正式发布 Elastic OpenTelemetry 分发版(Elastic Distributions of OpenTelemetry - EDOT),其中包含 Elastic 自定义版本的 OpenTelemetry Collector 以及多…...
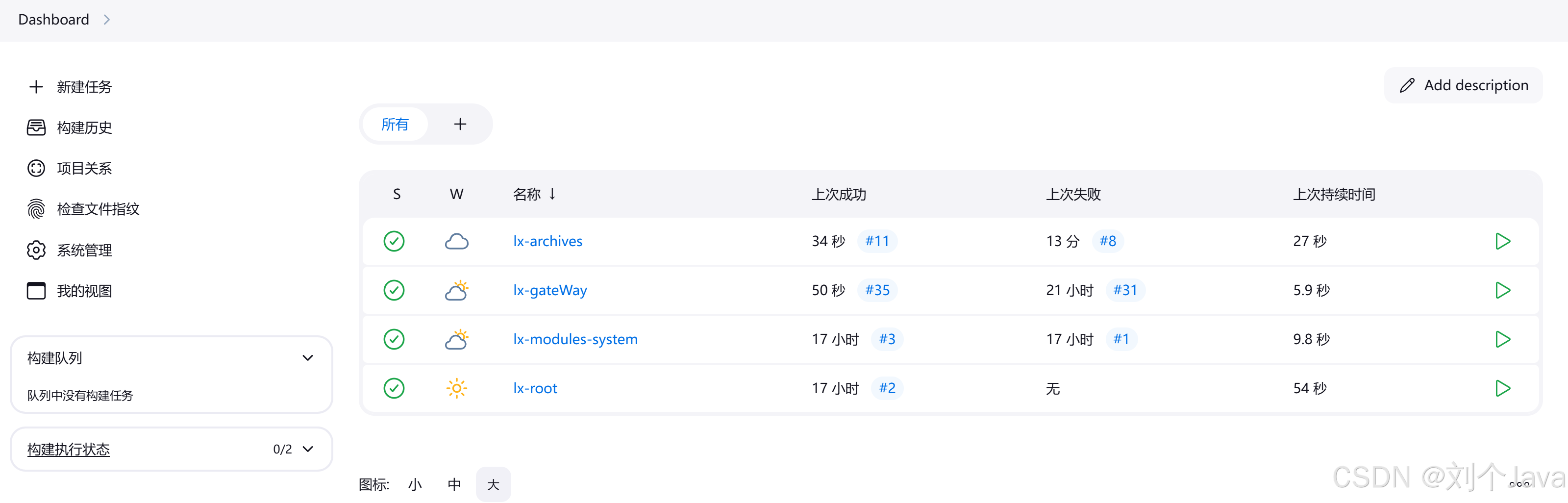
docker部署jenkins并成功自动化部署微服务
一、环境版本清单: docker 26.1.4JDK 17.0.28Mysql 8.0.27Redis 6.0.5nacos 2.5.1maven 3.8.8jenkins 2.492.2 二、服务架构:有gateway,archives,system这三个服务 三、部署步骤 四、安装linux 五、在linux上安装redis&#…...

UML对象图
UML对象图 一、对象图核心概念 对象图(Object Diagram)描述的是系统在某一时刻对象(实例)的状态快照。它关注的是实际对象之间的实例关系,而不是类与类之间的静态结构。主要特点有: 对象(Ob…...

【NLP 53、投机采样加速推理】
目录 一、投机采样 二、投机采样改进:美杜莎模型 流程 改进 三、Deepseek的投机采样 流程 Ⅰ、输入文本预处理 Ⅱ、引导模型预测 Ⅲ、候选集筛选(可选) Ⅳ、主模型验证 Ⅴ、生成输出与循环 骗你的,其实我在意透了 —— 25.4.4 一、…...

[250403] HuggingFace 新增检查模型与电脑兼容性的功能 | Firefox 发布137.0 支持标签组
目录 Hugging Face 让寻找兼容的 AI 模型变得更容易Firefox 137 版本更新摘要 Hugging Face 让寻找兼容的 AI 模型变得更容易 Hugging Face 是一个流行的在线平台,用于访问开源人工智能 (AI) 工具和模型。该平台推出了一项有用的新功能,允许个人轻松检查…...

VScode连接CentOS 7.6虚拟机
本文内容:在Windows上使用VMware运行虚拟机,然后使用VScode连接CentOS 7.6虚拟机。 进入系统前 安装VMware 安装教程参考:VMware安装 下载CentOS 7.6镜像 可以使用国内镜像源,但是一般国内镜像源要么已经不维护CentOS 7.6这个…...

Android Hilt 教程
Android Hilt 教程 —— 一看就懂,一学就会 1. 什么是 Hilt?为什么要用 Hilt? Hilt 是 Android 官方推荐的 依赖注入(DI)框架,基于 Dagger 开发,能够大大简化依赖注入的使用。 为什么要用 Hi…...

高德地图 3D 渲染-区域纹理图添加
引入-初始化地图(关键代码) // 初始化页面引入高德 webapi -- index.html 文件 <script src https://webapi.amap.com/maps?v2.0&key您申请的key值></script>// 添加地图容器 <div idcontainer ></div>// 地图初始化应该…...

K8S核心技术点
Pod,Service和Deployment的关系 Pod:Kubernetes 中最小的部署单元,用于运行容器化应用。 Service:提供服务发现和负载均衡,为 Pod 提供稳定的网络端点,ClusterIP,NodePort,LoadBala…...
)
Spring Boot 与 TDengine 的深度集成实践(二)
创建数据模型 定义实体类 在完成数据库连接配置后,我们需要创建与 TDengine 表对应的 Java 实体类。实体类是 Java 对象与数据库表之间的映射,通过定义实体类,我们可以方便地在 Java 代码中操作数据库中的数据,实现数据的持久化…...

搭建hadoop集群模式并运行
3.1 Hadoop的运行模式 先去官方看一看Apache Hadoop 3.3.6 – Hadoop: Setting up a Single Node Cluster. 本地模式:数据直接存放在Linux的磁盘上,测试时偶尔用一下 伪分布式:数据存放在HDFS,公司资金不足的时候用 完全分布式&a…...

Qt实现鼠标右键弹出弹窗退出
Qt鼠标右键弹出弹窗退出 1、鼠标右键实现1.1 重写鼠标点击事件1.2 添加头文件1.3 添加定义2、添加菜单2.1添加菜单头文件2.2创建菜单对象2.3 显示菜单 3、添加动作3.1添加动作资源文件3.2 添加头文件3.3 创建退出动作对象3.4菜单添加动作对象 4、在当前鼠标位置显示菜单4.1当前…...

Spring 服务调用接口时,提示You should be redirected automatically to target URL:
问题 <!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 3.2 Final//EN"><title>Redirecting...</title><h1>Redirecting...</h1><p>You should be redirected automatically to target URL: <a href"http://xxx/api/v1/branch…...

Springboot整合Mybatis+Maven+Thymeleaf学生成绩管理系统
前言 该系统为学生成绩管理系统,可以当作学习参考,也可以成为Spirng Boot初学者的学习代码! 系统描述 学生成绩管理系统提供了三种角色:学生,老师,网站管理员。主要实现的功能如下: 登录 &a…...

马井堂js设置倒计时页面
js-倒计时页面 提示:这里简述项目相关背景: 例如:项目场景:倒计时需求 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible&…...
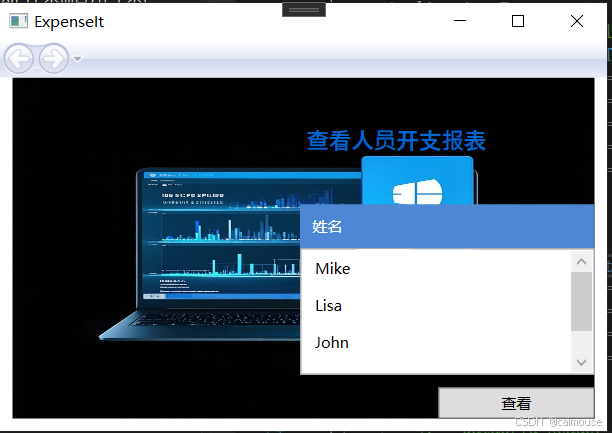
C#里第一个WPF程序
WPF程序对界面进行优化,但是比WINFORMS的程序要复杂很多, 并且界面UI基本上不适合拖放,所以需要比较多的时间来布局界面, 产且需要开发人员编写更多的代码。 即使如此,在面对诱人的界面表现, 随着客户对界面的需求提高,还是需要采用这样的方式来实现。 界面的样式采…...

【Java设计模式】第5章 工厂方法模式讲解
5. 工厂方法模式 5.1 工厂方法讲解 定义:定义一个创建对象的接口,由子类决定实例化的类,将对象创建延迟到子类。适用场景: 创建对象需要大量重复代码。客户端不依赖具体产品的创建细节。优点: 符合开闭原则,新增产品只需扩展子类。客户端仅依赖抽象接口,不依赖具体实现…...

PyTorch 生态迎来新成员:SGLang 高效推理引擎解析
SGLang 现已正式融入 PyTorch 生态系统!此次集成确保了 SGLang 符合 PyTorch 的技术标准与最佳实践,为开发者提供了一个可靠且社区支持的框架,助力大规模语言模型(LLM)实现高效且灵活的推理。 如需深入了解 PyTorch…...

时序数据库 TDengine Cloud 私有连接实战指南:4步实现数据安全传输与成本优化
小T导读:在物联网和工业互联网场景下,企业对高并发、低延迟的数据处理需求愈发迫切。本文将带你深入了解 TDengineCloud 如何通过全托管服务与私有连接,帮助企业实现更安全、更高效、更低成本的数据采集与传输,从架构解析到实际配…...

微服务注册中心选择指南:Eureka vs Consul vs Zookeeper vs Nacos
文章目录 引言微服务注册中心概述什么是服务注册与发现选择注册中心的标准 常见的微服务注册中心1. Eureka1.1 理论基础1.2 特点1.3 示例代码 2. Consul2.1 理论基础2.2 特点2.3 示例代码 3. Zookeeper3.1 理论基础3.2 特点3.3 示例代码 4. Nacos4.1 理论基础4.2 特点4.3 示例代…...

Java - WebSocket配置及使用
引入依赖 Spring Boot 默认支持 WebSocket,但需要引入 spring-boot-starter-websocket 依赖,然后重新构建项目 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</arti…...

厦门未来之音:科技与自然共舞的奇幻篇章
故事背景 故事发生在中国福建厦门,描绘未来城市中科技与传统文化深度融合的奇景。通过六大创新场景展现人与自然、历史与未来的和谐共生,市民在智能设施中感受文化传承的力量。 故事内容 从鼓浪屿的声波音乐栈道到BRT天桥上的空中茶园,从修复…...

React 列表与 Keys 的深入探讨
React 列表与 Keys 的深入探讨 在 React 中,列表渲染是一个常见的操作,而 Keys 是在列表渲染中一个非常重要的概念。本文将深入探讨 React 列表与 Keys 的关系,帮助开发者更好地理解并运用它们。 引言 React 是一个用于构建用户界面的 JavaScript 库,它的虚拟 DOM 和组件…...

【Python】Python 100题 分类入门练习题 - 新手友好
Python 100题 分类入门练习题 - 新手友好篇 - 整合篇 一、数学问题题目1:组合数字题目2:利润计算题目3:完全平方数题目4:日期天数计算题目11:兔子繁殖问题题目18:数列求和题目19:完数判断题目21…...
