【人工智能】AI大模型开发数学基础指南
目录
- 学习内容
- **1. 线性代数**
- **2. 概率与统计**
- **3. 微积分**
- **4. 优化理论**
- **5. 信息论**
- **6. 数值计算**
- **7. 离散数学**
- **8. 统计学进阶**
- **如何学习?**
- **总结**
- 如何学习
- **1. 明确学习目标**
- **2. 分阶段学习计划**
- **阶段 1:夯实基础**
- **阶段 2:掌握核心工具**
- **阶段 3:进阶应用**
- **3. 结合代码实践**
- **4. 从论文和模型中学习**
- **5. 避免常见误区**
- **6. 高效学习资源推荐**
- **7. 持续提升:从理论到科研**
- **总结**
学习内容
AI大模型开发需要扎实的数学基础,以下是核心数学领域及其应用场景:
1. 线性代数
- 重要性:神经网络的核心运算基于矩阵和张量操作。
- 关键内容:
- 矩阵乘法、特征值/特征向量(用于降维如PCA)。
- 张量运算(如卷积神经网络中的多维数据操作)。
- 奇异值分解(SVD)在模型压缩中的应用。
- 应用场景:全连接层计算、注意力机制(如Transformer中的QKV矩阵)。
2. 概率与统计
- 重要性:处理数据不确定性、评估模型性能。
- 关键内容:
- 概率分布(高斯分布、softmax输出)。
- 贝叶斯定理(贝叶斯优化、生成模型)。
- 统计指标(均值、方差、假设检验)。
- 应用场景:损失函数(交叉熵)、正则化(Dropout的期望)、数据分布建模。
3. 微积分
- 重要性:优化模型参数的核心工具。
- 关键内容:
- 梯度计算(反向传播的链式法则)。
- 多元函数的偏导数(优化高维参数空间)。
- 积分(概率密度函数、期望计算)。
- 应用场景:梯度下降法、损失曲面分析。
4. 优化理论
- 重要性:模型训练的数学本质是优化问题。
- 关键内容:
- 梯度下降法(SGD、Adam等优化器)。
- 凸优化与非凸优化(损失函数的性质)。
- 拉格朗日乘数法(处理约束问题如GAN)。
- 应用场景:学习率调整、参数更新策略设计。
5. 信息论
- 重要性:量化信息差异,指导模型设计。
- 关键内容:
- 熵、交叉熵(分类任务损失函数)。
- KL散度(评估生成模型质量)。
- 互信息(特征选择、对比学习)。
- 应用场景:模型压缩、损失函数设计(如BERT的MLM任务)。
6. 数值计算
- 重要性:确保算法实现的稳定性和效率。
- 关键内容:
- 数值稳定性(梯度爆炸/消失问题)。
- 迭代法(求解大规模线性系统)。
- 近似算法(如低秩近似加速计算)。
- 应用场景:参数初始化(Xavier/He)、归一化技术(LayerNorm)。
7. 离散数学
- 关键内容:
- 图论(图神经网络、注意力机制的结构表示)。
- 组合数学(模型架构搜索、排列组合问题)。
- 应用场景:知识图谱建模、Transformer中的序列关系。
8. 统计学进阶
- 关键内容:
- 假设检验(评估模型效果显著性)。
- 回归分析(线性模型基础)。
- 置信区间(不确定性估计)。
- 应用场景:A/B测试模型效果、数据预处理分析。
如何学习?
- 入门:掌握线性代数、概率统计、微积分和优化的基础概念。
- 进阶:结合具体模型(如Transformer、Diffusion)深入理解数学原理。
- 实践:通过PyTorch/TensorFlow实现算法,直观体会数学的应用。
总结
- 核心数学:线性代数、概率统计、微积分、优化理论。
- 延伸领域:信息论(模型设计)、数值计算(工程实现)。
- 学习建议:从理论推导过渡到代码实现,结合论文复现加深理解(如阅读Attention Is All You Need的矩阵运算部分)。
数学基础决定了能否深入理解模型本质,而非仅停留在调参层面。
如何学习
学习 AI 大模型所需的数学基础需要系统性和实践性结合,以下是分阶段的学习路径和方法:
1. 明确学习目标
- 核心目标:理解大模型(如Transformer、Diffusion、MoE等)的数学原理,而非成为数学专家。
- 优先级:线性代数 > 概率统计 > 微积分 > 优化理论 > 信息论 > 数值计算。
2. 分阶段学习计划
阶段 1:夯实基础
- 线性代数:
- 重点:矩阵运算、特征值分解、张量概念。
- 学习资源:
- 书籍:《线性代数应该这样学》(Sheldon Axler)或《矩阵分析》(Roger Horn)。
- 实践:用NumPy实现矩阵乘法、PCA降维。
- 概率与统计:
- 重点:概率分布、贝叶斯定理、期望与方差。
- 学习资源:
- 书籍:《概率导论》(Dimitri P. Bertsekas)。
- 实践:用Python模拟抛硬币、掷骰子,计算交叉熵损失。
阶段 2:掌握核心工具
- 微积分:
- 重点:梯度、链式法则、多元函数极值。
- 学习资源:
- 3Blue1Brown《微积分本质》系列视频(直观理解)。
- 实践:手动推导逻辑回归的梯度公式,用PyTorch实现自动微分。
- 优化理论:
- 重点:梯度下降、凸优化、拉格朗日乘数。
- 学习资源:
- 书籍:《Convex Optimization》(Boyd)第1-5章。
- 实践:实现SGD优化器,对比Adam和RMSProp的效果。
阶段 3:进阶应用
- 信息论:
- 重点:熵、KL散度、互信息。
- 学习资源:
- 书籍:《Elements of Information Theory》(Cover & Thomas)前4章。
- 实践:计算两个分布的KL散度,分析BERT的MLM损失函数。
- 数值计算:
- 重点:数值稳定性、矩阵条件数。
- 学习资源:
- 课程:Coursera《Numerical Methods for Engineers》。
- 实践:分析梯度爆炸/消失问题,实现LayerNorm。
3. 结合代码实践
- 核心原则:用代码实现数学公式,避免“纸上谈兵”。
- 示例:
- 用NumPy实现矩阵分解(如SVD)。
- 用PyTorch定义一个自定义损失函数(如带KL散度的VAE)。
- 手写反向传播(如2层神经网络的梯度计算)。
- 示例:
- 工具推荐:
- Jupyter Notebook:可视化矩阵运算、梯度下降过程。
- PyTorch/TensorFlow:自动微分库直接关联数学与代码。
- LaTeX:整理数学推导笔记(如Notion或Obsidian)。
4. 从论文和模型中学习
- 方法:
- 精读经典论文:如《Attention Is All You Need》,重点推导QKV矩阵运算和Softmax概率的意义。
- 复现简单模型:从线性回归开始,逐步实现Transformer的自注意力机制。
- 调试代码:在模型训练中监控梯度分布(如TensorBoard),理解数值不稳定的原因。
- 推荐资源:
- 《Dive into Deep Learning》(动手学深度学习)中的数学+代码结合案例。
- Hugging Face源码(如BERT的Attention层实现)。
5. 避免常见误区
- 不要死磕证明:优先理解数学工具的几何意义和应用场景(如特征值分解=坐标变换)。
- 不要孤立学习:将概率与损失函数结合、矩阵乘法与神经网络前向传播结合。
- 不要忽略工程细节:学习浮点数精度(FP32/FP16)对数值计算的影响。
6. 高效学习资源推荐
- 入门课程:
- 吴恩达《深度学习专项课程》(Coursera,侧重直观理解)。
- 3Blue1Brown《线性代数》《微积分》动画系列(B站/YouTube)。
- 进阶书籍:
- 《Deep Learning》(Ian Goodfellow)第2-4章(数学基础章节)。
- 《Mathematics for Machine Learning》(Deisenroth,剑桥大学教材)。
- 工具库:
- SymPy:符号计算库,辅助推导梯度公式。
- Einops:直观操作张量维度,强化线性代数思维。
7. 持续提升:从理论到科研
- 研究方向:
- 分析Transformer的梯度流(需微积分+数值计算)。
- 改进优化器(需优化理论+概率)。
- 设计稀疏大模型(需线性代数+信息论)。
- 社区互动:
- 参与AI数学研讨会(如MIT的Seminars on Mathematics of ML)。
- 在Kaggle/Papers With Code上复现数学密集型的模型(如Diffusion Model)。
总结
- 关键路径:基础数学 → 代码实现 → 模型复现 → 论文精读。
- 核心思维:将数学视为工具,而非目标。例如:
- 线性代数 = 数据的高维空间变换;
- 概率分布 = 模型对世界的建模方式;
- 梯度下降 = 在损失曲面上“导航”最优解。
- 终极检验:能否从零推导一个简单模型(如逻辑回归)的全部数学过程,并用代码实现。
数学是AI的“内功”,短期内可能枯燥,但一旦打通,对模型的理解会远超调参层面。坚持6个月的系统学习,你会发现自己能直接看懂论文公式,甚至提出改进思路!
相关文章:

【人工智能】AI大模型开发数学基础指南
目录 学习内容**1. 线性代数****2. 概率与统计****3. 微积分****4. 优化理论****5. 信息论****6. 数值计算****7. 离散数学****8. 统计学进阶****如何学习?****总结** 如何学习**1. 明确学习目标****2. 分阶段学习计划****阶段 1:夯实基础****阶段 2&…...

Express中间件(Middleware)详解:从零开始掌握(1)
1. 中间件是什么? 想象中间件就像一个"加工流水线",请求(Request)从进入服务器到返回响应(Response)的过程中,会经过一个个"工作站"进行处理。 简单定义:中间件是能够访问请求对象(req)、响应对象(res)和下…...

STM32单片机中EXTI的工作原理
目录 1. EXTI概述 2. EXTI的组成部分 3. 工作原理 3.1 引脚配置 3.2 中断触发条件 3.3 中断使能 3.4 中断处理 4. 使用示例 5. 注意事项 结论 在STM32单片机中,EXTI(外部中断)是一种用于处理外部事件的机制,能够提高对硬…...

现代工业测试的核心支柱:电机试验工作台?(北重机械厂家)
电机试验工作台是现代工业测试中的核心支柱之一。这种工作台通常用于对各种类型的电机进行性能测试、负载测试和耐久性测试。通过电机试验工作台,工程师可以评估电机的效率、功率输出、转速、扭矩、温度等关键参数,从而确保电机的设计符合要求࿰…...

oracle 11g密码长度和复杂度查看与设置
verify_function_11G 的密码复杂性要求: 密码长度至少为 8 个字符。 密码必须包含至少一个数字和一个字母字符。 密码不能与用户名相同或相似。 密码不能是服务器名或其变体。 密码不能是常见的弱密码(如 welcome1、oracle123 等)。 注意事项&…...

CVE-2025-32375 | Windows下复现 BentoML runner 服务器远程命令执行漏洞
目录 1. 漏洞描述2. 漏洞复现1. 安装 BentoML 1.4.72. 创建模型3. 构建模型4. 托管模型5. 执行exp 3. POC4. 补充学习 参考链接: https://mp.weixin.qq.com/s/IxLZr83RvYqfZ_eXhtNvgg https://github.com/bentoml/BentoML/security/advisories/GHSA-7v4r-c989-xh26 …...

某局jsvmp算法分析(dunshan.js/lzkqow23819/lzkqow39189)
帮朋友看一个税某局的加密算法。 传送门 (需要帐号登陆的 普通人没授权也看不了) 废话不多说直接抓包开干 这里可以看到一个headers中的加密参数 lzkqow23819 以及url路径里面的6eMrZlPH(这个有点像瑞数里面的) 还有就是cookies里面的这几个…...

深入剖析 Kafka 的零拷贝原理:从操作系统到 Java 实践
Kafka 作为一款高性能的分布式消息系统,其卓越的吞吐量和低延迟特性得益于多种优化技术,其中“零拷贝”(Zero-Copy)是核心之一。零拷贝通过减少用户态与内核态之间的数据拷贝,提升了 Kafka 在消息传输中的效率。本文将…...

AlmaLinux9.5 修改为静态IP地址
查看当前需要修改的网卡名称 ip a进入网卡目录 cd /etc/NetworkManager/system-connections找到对应网卡配置文件进行修改 修改配置 主要修改ipv4部分,改成自己的IP配置 [ipv4] methodmanual address1192.168.252.129/24,192.168.252.254 dns8.8.8.8重启网卡 …...

内联函数通常定义在头文件中的原因详解
什么是内联函数? 内联函数(inline function)是C中的一种函数优化机制,通过在函数声明前加上inline关键字,建议编译器将函数调用替换为函数体本身的代码,从而减少函数调用的开销。 为什么内联函数需要定义…...

操作系统 4.4-从生磁盘到文件
文件介绍 操作系统中对磁盘使用的第三层抽象——文件。这一层抽象建立在盘块(block)和文件(file)之间,使得用户可以以更直观和易于理解的方式与磁盘交互,而无需直接处理磁盘的物理细节如扇区(se…...
免费多语言文档翻译软件推荐
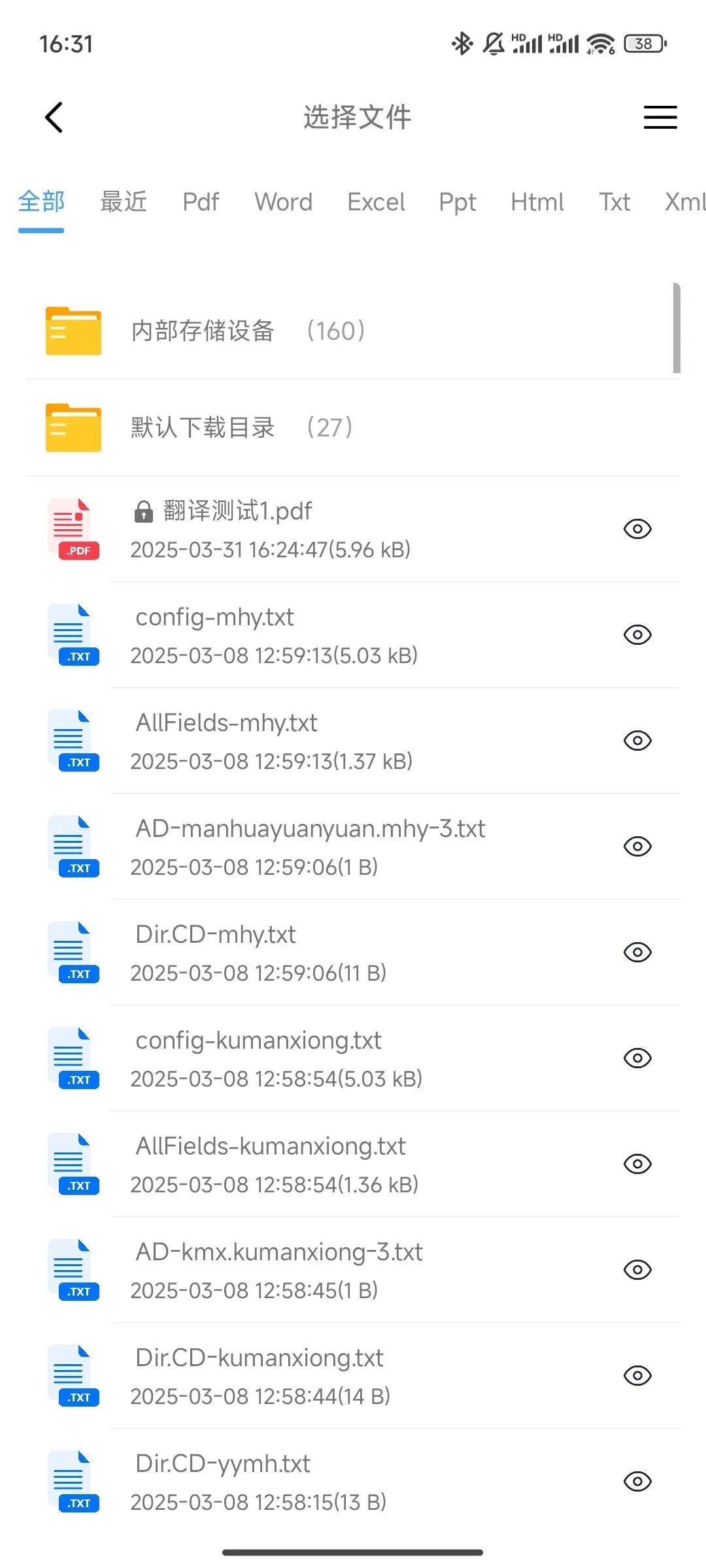
软件介绍 今天给大家介绍一款文档翻译助手。它能够支持PDF、Word等多种文档格式,涵盖中文、英文、日语等多语言互译。此软件在翻译过程中精选保留文档原貌,每段文字、每个图表的匹配都十分完美,还依托顶尖翻译大模型,让翻译结果符…...

安全序列(DP)
#include <bits/stdc.h> using namespace std; const int MOD1e97; const int N1e65; int f[N]; int main() {int n,k;cin>>n>>k;f[0]1;for(int i1;i<n;i){f[i]f[i-1]; // 不放桶:延续前一位的所有方案if(i-k-1>0){f[i](f[i]f[i-k…...

【Flask开发】嘿马文学web完整flask项目第4篇:4.分类,4.分类【附代码文档】
教程总体简介:2. 目标 1.1产品与开发 1.2环境配置 1.3 运行方式 1.4目录说明 1.5数据库设计 2.用户认证 Json Web Token(JWT) 3.书架 4.1分类列表 5.搜索 5.3搜索-精准&高匹配&推荐 6.小说 6.4推荐-同类热门推荐 7.浏览记录 8.1配置-阅读偏好 8.配置 9.1项目…...

SQL开发的智能助手:通义灵码在IntelliJ IDEA中的应用
SQL 是一种至关重要的数据库操作语言,尽管其语法与通用编程语言有所不同,但因其在众多应用中的广泛使用,大多数程序员都具备一定的 SQL 编写能力。然而,当面对复杂的 SQL 语句或优化需求时,往往需要专业数据库开发工程…...

基于 Q - learning 算法的迷宫导航
这段 Python 代码实现了一个基于 Q - learning 算法的迷宫导航系统。代码通过定义迷宫环境、实现 Q - learning 算法来训练智能体,使其能够在迷宫中找到从起点到终点的最优路径,同时利用训练好的 Q 表来测试智能体的导航能力。 在这个代码实现的迷宫环境…...

解决:AttributeError: module ‘cv2‘ has no attribute ‘COLOR_BGR2RGB‘
opencv AttributeError: module ‘cv2’ has no attribute ‘warpFrame’ 或者 opencv 没有 rgbd 解决上述问题的方法是: 卸载重装。 但是一定要卸载干净,仅仅卸载opencv-python是不行的。无限重复都报这个错。 使用pip list | grep opencv查看相关的…...

NutriJarvis:AI慧眼识餐,精准营养触手可及!—— 基于深度学习的菜品识别与营养计算系统
NutriJarvis:AI慧眼识餐,精准营养触手可及!—— 基于深度学习的菜品识别与营养计算系统 NutriJarvis 是一个基于深度学习的菜品识别与营养计算系统,旨在通过计算机视觉技术自动识别餐盘中的食物,并估算其营养成分&…...

作为一名java技术博主如何突围
作为一位Java开发和技术博主,想要在抖音上快速提升粉丝数量和视频播放量,可以结合以下策略进行优化: 1. 明确目标受众与技术方向 细分领域:技术领域广泛,可以专注于Java开发、算法、框架解析(如Spring Boo…...

【LaTeX】
基本使用 \documentclass 类型:文章(article)、报告(report)、书(book) 中文的文章是ctexart,中文字体是UTF8 \documentclass[UTF8]{ctexart} []说明可以省略不写的意思…...

细说STM32单片机FreeRTOS任务管理相关函数及多任务编程的实现方法
目录 一、FreeRTOS任务管理相关函数 1、FreeRTOS函数 2、FreeRTOS宏函数 3、主要函数功能说明 (1)创建任务osThreadNew() (2)删除任务vTaskDelete() (3)挂起任务vTaskSuspend() (4&…...

uniapp微信小程序基于wu-input二次封装TInput组件(支持点击下拉选择、支持整数、电话、小数、身份证、小数点位数控制功能)
一、 最终效果 二、实现了功能 1、支持输入正整数---设置specifyTypeinteger 2、支持输入数字(含小数点)---设置specifyTypedecimal,可设置decimalLimit来调整小数点位数 3、支持输入手机号--设置specifyTypephone 4、支持输入身份证号---设…...
)
VLM-R1GRPO微调,强化学习训练, 实战训练教程(2)
https://www.dong-blog.fun/post/2013 VLM-R1GRPO微调, 实战训练教程(1): https://www.dong-blog.fun/post/1961 本博客这次使用多图进行GRPO。 官方git项目:https://github.com/om-ai-lab/VLM-R1?tabreadme-ov-f…...

系统弹出消息功能,且保证用户只能获取弹出一次消息
要实现系统弹出消息功能,且保证用户只能获取弹出一次消息,你可以借助 Redis 来达成。基本思路是:把消息存于 Redis 的列表中,同时用 Redis 的集合记录用户是否已接收过该消息。下面是一个示例工具类,其中包含推送消息和…...

Python代码解释
文章目录 代码解析执行过程等价写法其他类似操作 这段代码使用了 Python 的 map() 函数和 lambda 表达式来对列表中的每个元素进行平方运算。让我详细解释一下: 代码解析 numbers [1, 2, 3, 4] squared list(map(lambda x: x**2, numbers))numbers [1, 2, 3, …...

GPIO_ReadInputData和GPIO_ReadInputDataBit区别
目录 1、GPIO_ReadInputData: 2、GPIO_ReadInputDataBit: 总结 GPIO_ReadInputData 和 GPIO_ReadInputDataBit 是两个函数,通常用于读取微控制器GPIO(通用输入输出)引脚的输入状态,特别是在STM32系列微控制器中。它们之间的主要…...

MySQL数据库编程总结
MySQL数据库编程总结 一、数据库概述 数据库定义 • 数据库是管理数据的软件系统,用于高效存储、管理和检索数据,减少冗余。 • 核心功能:通过SQL语言定义、操作数据,维护完整性和安全性。 常见数据库 • MySQL、Oracle、SQL Ser…...

leetcode-419.棋盘上的战舰
leetcode-419.棋盘上的战舰 文章目录 leetcode-419.棋盘上的战舰一.题目描述二.第一次代码提交三.第二次代码提交 一.题目描述 二.第一次代码提交 class Solution { public:int countBattleships(vector<vector<char>>& board) {int m board.size(); //列数i…...
使用uglifyjs对静态引入的js文件进行压缩
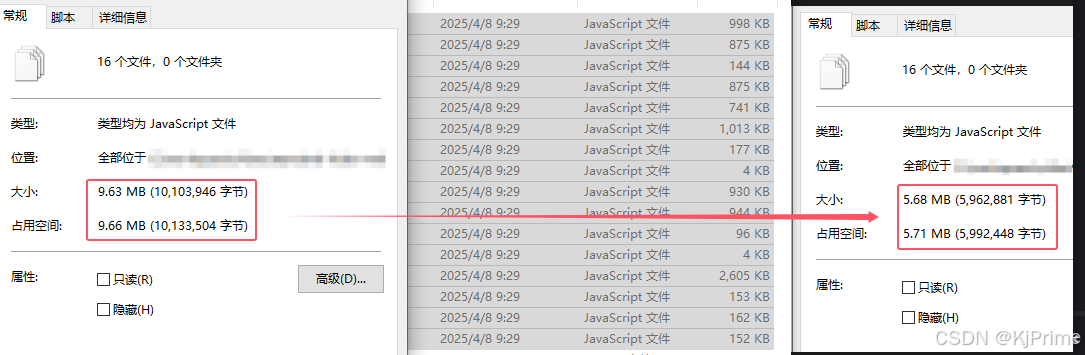
前言 因为有时候js文件没有npm包,或者需要修改,只能引入静态的js,那么这个时候就可以对js进行压缩了。我其实想通过vite、webpack等插件进行压缩的,可是他都不能定位到public目录下面的文件,所以我只能自己压缩了。编…...

ecovadis评分要求,如何提高ecovadis分数,未来展望
EcoVadis评分要求、提升方法及未来展望 1. EcoVadis评分概述 EcoVadis是全球领先的企业可持续发展评级平台,评估企业在环境(E)、劳工与人权(L)、商业道德(B)、可持续采购(S&#x…...
