2025年第十六届蓝桥杯省赛C++ A组真题
2025年第十六届蓝桥杯省赛C++ A组真题
- 1.说明
- 2.题目A:寻找质数(5分)
- 3.题目B:黑白棋(5分)
- 4. 题目C:抽奖(10分)
- 5. 题目D:红黑树(10分)
- 6. 题目E:黑客(15分)
- 7. 题目F:好串的数目(15分)
- 8. 题目G:地雷阵(20分)
- 9. 题目H:扫地机器人(20分)
1.说明
真题来源于十六届蓝桥杯赛后直播间,受大风天气影响的地区(北京、天津和河北)题目应该会变动,我这里参加的实际是河北C++研究生组。考虑到时间关系,将重点放在写研究生组真题上,所以C++ A组题目主要放题目资料,这里的题目要是想短时间给写出来还是太有挑战了,之后如果研究生组的题目看的差不多了再回来补一下A组题目,好像A组题目和研究生组题目难度差不多。
2.题目A:寻找质数(5分)
如果一个正整数只能被 1 和它本身两个数整除,就称为一个质数。最小的几个质数依次是 2,3,5,7,11,13,···,请问,第 2025 个质数是多少?
#include <iostream>
#include <cmath>// 判断一个数是否为质数
bool isPrime(int num) {if (num < 2) return false;for (int i = 2; i <= std::sqrt(num); ++i) {if (num % i == 0) return false;}return true;
}int main() {int count = 0;int num = 2;while (true) {if (isPrime(num)) {++count;if (count == 2025) {std::cout << "第 2025 个质数是: " << num << std::endl;break;}}++num;}return 0;
}
3.题目B:黑白棋(5分)
小蓝最近迷上了一款名为“黑白棋填充”的游戏。该游戏在一个方形网格棋盘上进行,其中部分格子已经填有黑色或白色的棋子,而其他格子为空,等待玩家填入棋子。游戏规则是,玩家需要按照以下规则填满整个棋盘,才能算作胜利:
(1) 黑白棋子数量均等:在每一行和每一列中,黑色棋子和白色棋子的数量必须相等。
(2)相邻棋子限制:在棋盘的任何一行或一列中,不能有超过两个相同颜色的棋子连续排列(即不允许出现“黑黑黑”或“白白白”的情况)。
(3)行列唯一性:每一行的棋子排列方式必须是唯一的,不能与棋盘中的任何其他行完全相同。每一列的棋子排列方式必须是唯一的,不能与棋盘中的任何其他列完全相同。行与列之间的棋子排列不作比较,即行可以与列相同,无需满足行列间的唯一性。

提示:二进制表示法搜索剪枝。100000000000000000001000001100001111。
4. 题目C:抽奖(10分)
LQ 商场为了回馈广大用户,为在此消费的用户提供了抽奖机会:抽奖机有三个转轮,每个转轮上都分布有 n 个数字图案,标号为 1 ~ n ,按照从 1 到 n 顺序转动,当转到第 n 个图案时会从第一个继续开始。奖项如下:
(1)三个相同的图案,积分 +200 ;
(2)两个相同的图案,积分 +100 ;
(3)三个数字图案,从左到右连续(例如 1,2,3 ),积分 +200 ;
(4)三个数字图案,经过顺序调整后连续(例如 2,1,3 或 3,2,1 ),积分 +100 ;
抽奖机处于初始状态,三个转轮都处于第一个位置。每次开始抽奖,都会产生三个对应的随机数 xi1,xi2 ,xi3 ,表示第 j 个转轮会向后转动 xij 次停下。下次抽奖时,转轮会从上一次转动后的位置开始继续转动。
注意,一次抽奖最多只能获得一次积分,如果同时命中多个奖项,以积分最大的那个奖项为准。请问,如果执行 m 次抽奖,总积分值是多少?
【输入格式】
输入的第一行包含一个正整数 n,表示转轮大小。
第二行包含 n 个正整数 a 1 , a 2 , ⋯ , a n a_1,a_2,\cdots,a_n a1,a2,⋯,an,依次表示第一个转轮上的数字图案,相邻整数之间使用一个空格分隔。
第三行包含 n 个正整数 b 1 , b 2 , ⋯ , b n b_1,b_2,\cdots,b_n b1,b2,⋯,bn,依次表示第二个转轮上的数字图案,相邻整数之间使用一个空格分隔。
第四行包含 n 个正整数 c 1 , c 2 , ⋯ , c n c_1,c_2,\cdots,c_n c1,c2,⋯,cn,依次表示第三个转轮上的数字图案,相邻整数之间使用一个空格分隔。
第五行包含一个整数 m,表示抽奖次数。
接下来 ( m ) 行,每行包含三个正整数 (xi1,xi2,xi3),相邻整数之间使用一个空格分隔。
【输出格式】
输出一行包含一个整数表示答案,即 ( m ) 次抽奖累计获得的积分的值。
【样例输入】
4
3 2 4 1
2 2 2 2
4 3 0 9
3
4 4 4
3 1 1
40 39 2
【样例输出】
300
【样例说明】
三个转轮在初始状态下都在位置 1。
第一次抽奖,三个转轮都转动 4 次,都转一整圈到达位置 1,三个转轮上的数字图案分别是 3、2、4,积分 +100;
第二次抽奖,第一个转轮转动 3 次到达位置 4,第二个转轮转动 1 次到达位置 2,第三个转轮转动 1 次到达位置 2,三个转轮上的数字图案分别是 1、2、3,积分 +200;
第三次抽奖,第一个转轮转动 40 次到达位置 4,第二个转轮转动 39 次到达位置 1,第三个转轮转动 2 次到达位置 4,三个转轮上的数字图案分别是 1、2、9,积分不增加。
因此总积分为 300。
5. 题目D:红黑树(10分)
【问题描述】
小蓝最近学习了红黑树,红黑树是一种特殊的二叉树,树上的结点有两种类型:红色结点和黑色结点。
小蓝在脑海中构造出一棵红黑树,构造方式如下:
(1)根结点是一个红色结点;
(2)如果当前结点 curNode 是红色结点,那么左子结点 curNode.left 是红色结点,右子结点 curNode.right 是黑色结点;
(3)如果当前结点 curNode 是黑色结点,那么左子结点 curNode.left 是黑色结点,右子结点 curNode.right 是红色结点;
此二叉树前几层的形态如下图所示:

【输入格式】
输入的第一行包含一个正整数 ( m ),表示小蓝挑选的结点数。
接下来 ( m ) 行,每行包含两个正整数 (ni,ki),用一个空格分隔,表示小蓝挑选的结点是第 ni 行(从上往下数)第 ki 个(从左往右数)结点。
【输出格式】
输出 ( m ) 行,每行包含一个字符串,依次表示小蓝每次挑选的结点的答案。RED 表示红色结点,BLACK 表示黑色结点。
【样例输入】
2
1 1
2 2
【样例输出】
RED
BLACK
6. 题目E:黑客(15分)
【问题描述】
小蓝正在两台电脑之间拷贝数据,数据是一个 (n×m) 大小的正整数矩阵,因此总共有 (n×m + 2) 个由空格分开的整数,其中前两个整数分别为 (n) 和 (m)。然而,有黑客入侵了小蓝的电脑,导致这 (n×m + 2) 个正整数的顺序被打乱了,小蓝想知道最多可能有多少个不同的原矩阵。
两个矩阵相同当且仅当它们行数相同、列数分别相同,且每个位置上的数相同。
【输入格式】
输入的第一行包含一个正整数 (n×m + 2)。
第二行包含 (n×m + 2) 个正整数 (a1,a2,…,an×m + 2),相邻整数之间使用一个空格分隔。
【输出格式】
输出一行包含一个整数表示答案。答案可能很大,请输出答案除以 1000000007 的余数。
【样例输入】
2 2 1 4 3 3
【样例输出】
24
7. 题目F:好串的数目(15分)
【问题描述】
对于一个长度为 (n) 的字符串 (s = s0s1…sn-1) 来说,子串的定义是从中选出两个下标 l,r(0 ≤ l ≤ r ≤n-1),这之间所有的字符组合起来的一个新的字符串:(s’ = sl…sr) 就是其中一个子串。
现在给出一个只有数字字符 0~9 组成的数字字符串,小蓝想要知道在其所有的子串中,有多少个子串是好串。一个子串是好串,当且仅当它满足以下两个条件之一:
(1)单字符子串一定是好串,即当子串长度为 1 时,它总是好串;
(2)长度大于 1 时,可以拆分为两个连续非递减子串。
其中,一个串 (p = p0p1…pn-1) 为连续非递减子串是指,对于所有 (1≤ i < k),满足 (pi = pi-1) 或 (pi = pi-1+1)。即数字串中的每一个数字,要么等于上一个数字,要么等于上一个数字加 1。例如 12233、456 是连续非递减子串。
【输入格式】
输入一行包含一个字符串 (s)。
【输出格式】
输出一行包含一个整数表示答案,即好串的数目。
【样例输入】
12258
【样例输出】
12
【样例说明】
长度为1的好串:1、2、2、5、8。它们长度都为1,都是好串。
长度为2的好串:12、22、25、58。12可以分割为1、2两个连续非递减子串,其它类似。
长度为3的好串:122、225。122可以分割为12、2两个连续非递减子串;225可以分割为22、5两个连续非递减子串。
长度为4的好串:1225。1225可以分割为122、5两个连续非递减子串。
总计12个好串。
8. 题目G:地雷阵(20分)
【问题描述】
小蓝正在平面直角坐标系中的第一象限里玩一个逃生小游戏,在第一象限中埋有 (n) 颗地雷,第 i 颗地雷的坐标为 (xi, yi),触发范围为以 (xi, yi) 为圆心,半径为 ri 的圆。一旦小蓝走进了圆内就会触发地雷导致游戏失败。小蓝初始在原点 (0,0) 上,他需要在第一象限内选择一个方向一直往前走,如果能不触发任何地雷即可成功通关游戏。他想知道在 [0,π/2] 中均匀随机选择一个方向,即在 (0°)(朝向 x 轴正方向)至 90°(朝向 y 轴正方向)之间随机选择一个方向,通关游戏的概率是多少?
【输入格式】
输入的第一行包含一个正整数 (n)。
接下来 (n) 行,每行包含三个正整数 (xi, yi),相邻整数之间使用一个空格分隔。
【输出格式】
输出一行包含一个实数,四舍五入保留三位小数,表示答案。
【样例输入】
2
1 3 1
3 1 1
【样例输出】
0.181
9. 题目H:扫地机器人(20分)
【问题描述】
在一个含有 n 个点 n 条边的无重边无自环的连通无向图中,有一个扫地机器人在执行清扫作业,其中结点 i 的标记 ti ∈{0, 1},如果为 1,则说明该结点需要进行清扫,扫地机器人在到达这个结点时会顺便进行清扫工作。机器人想知道,如果选定任意结点出发,每条边只能经过一次的话,最多能清扫多少个待清扫结点?
【输入格式】
输入的第一行包含一个正整数 n。
第二行包含 n 个整数 t1, t2, … , tn,相邻整数之间使用一个空格分隔。
接下来 n 行,每行包含两个正整数 ui, vi,用一个空格分隔,表示结点 ui 和结点 vi 之间有一条边。
【输出格式】
输出一行包含一个整数表示答案。
【样例输入】
9
1 0 1 0 0 1 1 0 1
2 8
2 9
2 5
1 5
1 3
1 4
4 5
4 6
6 7
【样例输出】
4
【样例说明】
其中一种路线:3 → 1 → 4 → 6 → 7。
到这里就结束啦,整理不易,欢迎关注【Jerry说前后端】、点赞并分享,获取更多前端和算法知识。
相关文章:

2025年第十六届蓝桥杯省赛C++ A组真题
2025年第十六届蓝桥杯省赛C A组真题 1.说明2.题目A:寻找质数(5分)3.题目B:黑白棋(5分)4. 题目C:抽奖(10分)5. 题目D:红黑树(10分)6. 题…...

asp.net Kestrel 和iis区别
Kestrel 和 IIS 都是用于托管 Web 应用程序的服务器,不过它们在多个方面存在显著差异,下面为你详细分析: 1. 所属平台与跨平台能力 Kestrel:是.NET Core 及后续版本的一部分,具备跨平台特性,可在 Windows…...

《植物大战僵尸融合版v2.4.1》,塔防与创新融合的完美碰撞
《植物大战僵尸融合版》是基于经典塔防游戏《植物大战僵尸》的创意同人改版,由“蓝飘飘fly”等开发者主导制作。它在保留原版核心玩法的基础上,引入了独特的植物融合机制,玩家可以将不同的植物进行组合,创造出全新的植物种类&…...

SGP4 基于C、C++安装指南
简介:SGP4 是一个用于简化轨道摄动模型的开源项目。 依赖:GCC/CLang, CMake 下载:GitCode - 全球开发者的开源社区,开源代码托管平台 (https://gitcode.com/gh_mirrors/sg/sgp4)或者从我的资源下载 https…...

SBTI认证的意义,什么是SBTI认证,sbti科学碳目标的好处
SBTI认证的意义与科学碳目标(SBT)的好处 1. 什么是SBTI认证? SBTI(Science Based Targets initiative,科学碳目标倡议)是由全球环境信息研究中心(CDP)、联合国全球契约(…...

[LeetCode 1696] 跳跃游戏 6(Ⅵ)
题面: LeetCode 1696 数据范围: 1 ≤ n u m s . l e n g t h , k ≤ 1 0 5 1 \le nums.length, \ k \le 10^5 1≤nums.length, k≤105 − 1 0 4 ≤ n u m s [ i ] ≤ 1 0 4 -10^4 \le nums[i] \le 10^4 −104≤nums[i]≤104 思路 & Code 重点&…...

在思科模拟器show IP route 发现Gateway of last resort is not set没有设置最后的通道
如果在show ip route的时候出现没有设置最后的通道Gateway of last resort is not set Switch#show ip route Codes: C - connected, S - static, I - IGRP, R - RIP, M - mobile, B - BGPD - EIGRP, EX - EIGRP external, O - OSPF, IA - OSPF inter areaN1 - OSPF NSSA exte…...

Redis 常问知识
1.Redis 缓存穿透问题 缓存穿透:当请求的数据在缓存和数据库中不存在时,该请求就跳出我们使用缓存的架构(先从缓存找,再从数据库查找、这样就导致了一直去数据库中找),因为这个数据缓存中永远也不会存在。…...

履带小车+六轴机械臂(2)
本次介绍原理图部分 开发板部分,电源供电部分,六路舵机,PS2手柄接收器,HC-05蓝牙模块,蜂鸣器,串口,TB6612电机驱动模块,LDO线性稳压电路,按键部分 1、开发板部分 需要注…...

多卡集群 - Docker命令来启动一个容器的实例
一、Docker下载安装及相关配置 桌面版:Docker Desktop: The #1 Containerization Tool for Developers | Docker 服务器版:Install | Docker Docs 我们先以windows桌面版为例进行安装,一般在公司里会使用服务器版本,后期也会出一…...

测试第三课-------自动化测试相关
作者前言 🎂 ✨✨✨✨✨✨🍧🍧🍧🍧🍧🍧🍧🎂 🎂 作者介绍: 🎂🎂 🎂 🎉🎉🎉…...

【C++教程】进制转换的实现方法
在C中进行进制转换可以通过标准库函数或自定义算法实现。以下是两种常见场景的转换方法及示例代码: 一、使用C标准库函数 任意进制转十进制 #include <string> #include <iostream>int main() {std::string num "1A3F"; // 十六进制数int…...

科普:如何通过ROC曲线,确定二分类的“理论阈值”
在二分类问题中,已知预测概率(如逻辑回归、神经网络输出的概率值)时,阈值的选择直接影响分类结果(正/负样本判定)。 一、实践中的阈值选择方法 1. 基于业务目标的调整 最大化准确率:适用于样…...

ebpf: CO-RE, BTF, and Libbpf(二)
本文内容主要来源于Learning eBPF,可阅读原文了解更全面的内容。 本文涉及源码也来自于书中对应的github:https://github.com/lizrice/learning-ebpf/ 概述 上篇文章主要讲了CO-RE最关键的一环:BTF,了解其如何记录内核中的数据结…...

祁连山国家公园shp格式数据
地理位置 祁连山国家公园位于中国西北部,横跨甘肃省与青海省交界处,主体处于青藏高原东北边缘。总面积约5.02万平方公里,是中国首批设立的10个国家公园之一。 设立背景 保护措施 文化与历史 旅游与教育 意义与挑战 祁连山国家公园的设立标志…...

《AI大模型应知应会100篇》 第16篇:AI安全与对齐:大模型的灵魂工程
第16篇:AI安全与对齐:大模型的灵魂工程 摘要 在人工智能技术飞速发展的今天,大型语言模型(LLM)已经成为推动社会进步的重要工具。然而,随着这些模型能力的增强,如何确保它们的行为符合人类的期…...

探索QEMU-KVM虚拟化:麒麟系统下传统与云镜像创建虚拟机的最佳实践
随着云计算和虚拟化技术的不断进步,虚拟化在管理服务器、隔离资源以及提升性能方面的好处越来越明显。麒麟操作系统Kylin OS是我们国家自己开发的操作系统,在政府机构和企业中用得很多。这篇文章会教你如何在麒麟操作系统上设置QEMU-KVM虚拟化环境&#…...

[ComfyUI] 最新控制模型EasyControl,吉卜力风格一键转绘
一、EasyControl介绍 玩ComfyUI的都知道Controlnet的重要性,可以根据约束来引导图片的生成,这也是ComfyUI商业化里面很重要的一环。 不过之前我们用的Controlnet都是基于Unet技术框架下的。 最近出的这个EasyControl有点不一样,是基于DiT&a…...

项目执行中的目标管理:从战略到落地的闭环实践
——如何让目标不“跑偏”、团队不“掉队”? 引言:为什么目标管理决定项目成败? 根据PMI研究,47%的项目失败源于目标模糊或频繁变更。在复杂多变的项目环境中,目标管理不仅是制定KPI,更是构建“方向感-执行…...

《计算机视觉度量:从特征描述到深度学习》—深度学习工业检测方案评估
谢谢各位粉丝的支持,过去了一年多才再次更新技术博客。原因是个人家庭和技术发展在这短短一年多,发生了很大变化。本人身为技术博主,也在不断的探索和研究新技术在工业检测领域的技术方案。 并在这期间已经完成了基础的工业检测大模型的设计…...

网页防篡改与盗链防护:实时监控与自动化修复实践
摘要:针对网页内容篡改与盗链问题,本文基于群联AI云防护系统,详解如何通过哈希校验、实时监控与CDN联动实现秒级修复,并提供Python与AWS S3集成代码。 一、网页安全的核心需求 防篡改:保障页面内容完整性,…...

LR(0)
LR0就是当我处在自动机为红色这些结束状态的时候,这些红色状态就代表我们识别到了一个句柄,那现在的问题就是识别到了句柄,那要不要对他进行归约?LR0就是我不管当前指针指向的终结符是什么,我都拿它做规约 这里的二号状…...

鸿蒙开发-页面跳转
1.路由使用 //1.引入路由 import router from ohos.router//2.使用跳转router.pushUrl({url: "pages/Show"})2.页面跳转 import { router } from kit.ArkUI;Entry Component struct LoginPage {State message: string 登陆页;build() {Row() {Column() {Text(this…...

#MES系统中的一些相关的名词
📌MES系统 部分 术语表 缩写英文全称中文名称详细解释MESManufacturing Execution System制造执行系统用于连接计划系统与生产现场,实时管理和控制整个生产过程,覆盖物料、人员、设备、质量、指令等。ERPEnterprise Resource Planning企业资…...
无人船 | 图解基于视线引导(LOS)的无人艇制导算法
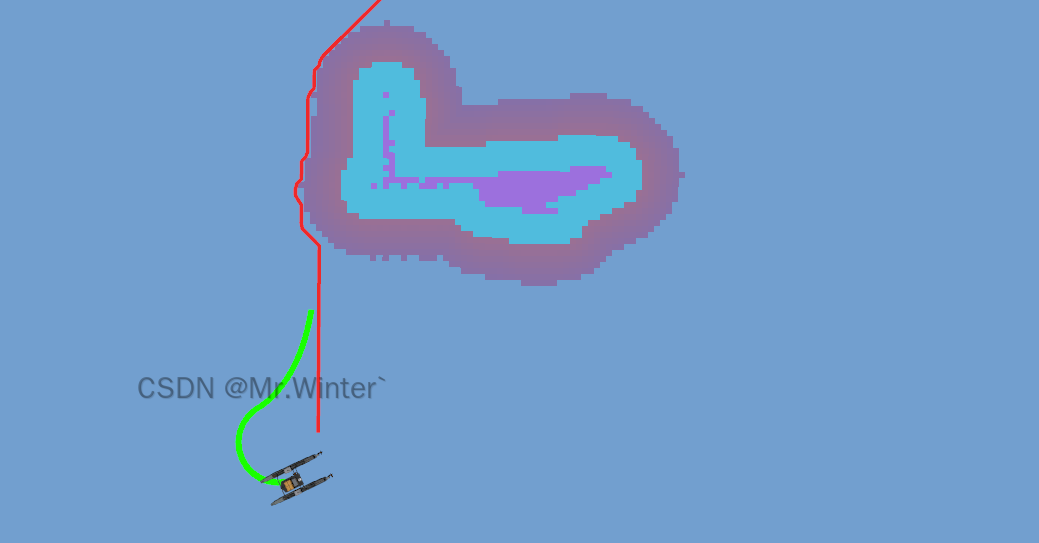
目录 1 视线引导法介绍2 LOS制导原理推导3 Lyapunov稳定性分析4 LOS制导效果 1 视线引导法介绍 视线引导法(Line of Sight, LOS)作为无人水面艇(USV)自主导航领域的核心技术,通过几何制导与动态控制深度融合的机制&am…...

LeetCode LCR157 套餐内商品的排列顺序
生成字符串的全部排列(去重):从问题到解决方案的完整解析 问题背景 在编程和算法设计中,生成字符串的所有排列是一个经典问题。它不仅出现在算法竞赛中,也在实际开发中有着广泛的应用,比如生成所有可能的…...

3.2.2.3 Spring Boot配置拦截器
在Spring Boot应用中配置拦截器(Interceptor)可以对请求进行预处理和后处理,实现如权限检查、日志记录等功能。通过实现HandlerInterceptor接口并注册到Spring容器,拦截器可以自动应用到匹配的请求路径。案例中,创建了…...

cryptozombies合约6
我们就快完成我们的随机僵尸制造器了,来写一个公共的函数把所有的部件连接起来。 写一个公共函数,它有一个参数,用来接收僵尸的名字,之后用它生成僵尸的DNA。 实战演习 创建一个 public 函数,命名为 createRandomZom…...

大模型文生图
提示词分4个部分:质量,主体,元素,风格 质量:杰作,高质量,超细节,完美的精度,高分辨率,大师级的; 权重:把图片加括号,&am…...

.NET MCP 示例
服务器端示例 基础服务器 以下是一个基础的 MCP 服务器示例,它使用标准输入输出(stdio)作为传输方式,并实现了一个简单的回显工具: using Microsoft.Extensions.DependencyInjection; using Microsoft.Extensions.H…...
