力扣每日打卡 1534. 统计好三元组 (简单)
力扣 1534. 统计好三元组 简单
- 前言
- 一、题目内容
- 二、解题方法
- 1. 暴力解法
- 2.官方题解
- 2.1 方法一:枚举
- 2.2 方法二:枚举优化
前言
这是刷算法题的第十二天,用到的语言是JS
题目:力扣 1534. 统计好三元组 (简单)
一、题目内容
给你一个整数数组 arr ,以及 a、b 、c 三个整数。请你统计其中好三元组的数量。
如果三元组 ( a r r [ i ] , a r r [ j ] , a r r [ k ] ) (arr[i], arr[j], arr[k]) (arr[i],arr[j],arr[k]) 满足下列全部条件,则认为它是一个 好三元组 。
- 0 < = i < j < k < a r r . l e n g t h 0 <= i < j < k < arr.length 0<=i<j<k<arr.length
- ∣ a r r [ i ] − a r r [ j ] ∣ < = a |arr[i] - arr[j]| <= a ∣arr[i]−arr[j]∣<=a
- ∣ a r r [ j ] − a r r [ k ] ∣ < = b |arr[j] - arr[k]| <= b ∣arr[j]−arr[k]∣<=b
- ∣ a r r [ i ] − a r r [ k ] ∣ < = c |arr[i] - arr[k]| <= c ∣arr[i]−arr[k]∣<=c
其中 ∣ x ∣ |x| ∣x∣ 表示 x x x 的绝对值。
返回 好三元组的数量 。
示例 1:
输入:arr = [3,0,1,1,9,7], a = 7, b = 2, c = 3
输出:4
解释:一共有 4 个好三元组:[(3,0,1), (3,0,1), (3,1,1), (0,1,1)] 。
示例 2:
输入:arr = [1,1,2,2,3], a = 0, b = 0, c = 1
输出:0
解释:不存在满足所有条件的三元组。
提示:
- 3 < = a r r . l e n g t h < = 100 3 <= arr.length <= 100 3<=arr.length<=100
- 0 < = a r r [ i ] < = 1000 0 <= arr[i] <= 1000 0<=arr[i]<=1000
- 0 < = a , b , c < = 1000 0 <= a, b, c <= 1000 0<=a,b,c<=1000
二、解题方法
1. 暴力解法
三重for循环
代码如下(实例):
/*** @param {number[]} arr* @param {number} a* @param {number} b* @param {number} c* @return {number}*/
var countGoodTriplets = function (arr, a, b, c) {// 暴力算法let count = 0for (let i = 0; i < arr.length; i++) for (let j = i + 1; j < arr.length; j++) for (let k = j + 1; k < arr.length; k++) if (Math.abs(arr[i] - arr[j]) <= a && Math.abs(arr[j] - arr[k]) <= b && Math.abs(arr[i] - arr[k]) <= c) count++return count
}
2.官方题解
2.1 方法一:枚举
思路与算法
用 O ( n 3 ) O(n^3) O(n3) 的循环依次枚举所有的 ( i , j , k ) (i,j,k) (i,j,k),这里 0 ≤ i < j < k < a r r . l e n g t h 0≤i<j<k<arr.length 0≤i<j<k<arr.length,对于每组 ( i , j , k ) (i,j,k) (i,j,k),判断 a r r [ i ] 、 a r r [ j ] 、 a r r [ k ] arr[i]、arr[j]、arr[k] arr[i]、arr[j]、arr[k] 是否满足条件。
最终统计出所有满足条件的三元组的数量。
代码如下(示例):
var countGoodTriplets = function(arr, a, b, c) {const n = arr.length;let cnt = 0;for (let i = 0; i < n; ++i) {for (let j = i + 1; j < n; ++j) {for (let k = j + 1; k < n; ++k) {if (Math.abs(arr[i] - arr[j]) <= a && Math.abs(arr[j] - arr[k]) <= b && Math.abs(arr[i] - arr[k]) <= c) {++cnt;}}}}return cnt;
};作者:力扣官方题解
链接:https://leetcode.cn/problems/count-good-triplets/solutions/371340/tong-ji-hao-san-yuan-zu-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
- 复杂度分析:
- 时间复杂度: O ( n 3 ) O(n^3) O(n3),其中 n n n 是数组 a r r arr arr 的长度。
- 空间复杂度: O ( 1 ) O(1) O(1)
链接:力扣本题官方题解
来源:力扣(LeetCode)
2.2 方法二:枚举优化
思路与算法
我们考虑 O ( n 2 ) O(n^2) O(n2) 枚举满足 ∣ a r r [ j ] − a r r [ k ] ∣ ≤ b ∣arr[j]−arr[k]∣≤b ∣arr[j]−arr[k]∣≤b 的二元组 ( j , k ) (j,k) (j,k),统计这个二元组下有多少 i i i 满足条件。由题目已知 i i i 的限制条件为 ∣ a r r [ i ] − a r r [ j ] ∣ ≤ a ∣arr[i]−arr[j]∣≤a ∣arr[i]−arr[j]∣≤a && ∣ a r r [ i ] − a r r [ k ] ∣ ≤ c ∣arr[i]−arr[k]∣≤c ∣arr[i]−arr[k]∣≤c,我们可以拆开绝对值,得到符合条件的值一定是 [ a r r [ j ] − a , a r r [ j ] + a ] [arr[j]−a,arr[j]+a] [arr[j]−a,arr[j]+a] 和 [ a r r [ k ] − c , a r r [ k ] + c ] [arr[k]−c,arr[k]+c] [arr[k]−c,arr[k]+c] 两个区间的交集,我们记为 [ l , r ] [l,r] [l,r]。因此,在枚举 ( j , k ) (j,k) (j,k) 这个二元组的时候,我们只需要快速统计出满足 i < j i<j i<j 且 a r r [ i ] arr[i] arr[i] 的值域范围在 [ l , r ] [l,r] [l,r] 的 i i i 的个数即可。
很容易想到维护一个 a r r [ i ] arr[i] arr[i] 频次数组的前缀和 s u m sum sum,对于一个二元组 ( j , k ) (j,k) (j,k),我们可以 O ( 1 ) O(1) O(1) 得到答案为 s u m [ r ] − s u m [ l − 1 ] sum[r]−sum[l−1] sum[r]−sum[l−1]。考虑怎么维护保证当前频次数组存的数的下标符合 i < j i<j i<j 的限制,我们只要从小到大枚举 j j j,每次 j j j 移动指针加一的时候,将 a r r [ j ] arr[j] arr[j] 的值更新到 s u m sum sum 数组中即可,这样能保证枚举到 j j j 的时候 s u m sum sum 数组里存的值的下标满足限制。
「将 a r r [ j ] arr[j] arr[j] 的值更新到 s u m sum sum 数组中」这个操作在本方法中是暴力更新,因为数组的值域上限很小,有能力的读者可以考虑怎么在进一步优化这一部分的复杂度,可以从离散化或者树状数组的角度考虑,这里不再赘述。
代码如下(示例):
var countGoodTriplets = function(arr, a, b, c) {const n = arr.length, sum = new Array(1001).fill(0);let ans = 0;for (let j = 0; j < n; ++j) {for (let k = j + 1; k < n; ++k) {if (Math.abs(arr[j] - arr[k]) <= b) {const lj = arr[j] - a, rj = arr[j] + a;const lk = arr[k] - c, rk = arr[k] + c;const l = Math.max(0, Math.max(lj, lk)), r = Math.min(1000, Math.min(rj, rk));if (l <= r) {if (l === 0) {ans += sum[r];}else {ans += sum[r] - sum[l - 1];}}}}for (let k = arr[j]; k <= 1000; ++k) {sum[k] += 1;}}return ans;
};作者:力扣官方题解
链接:https://leetcode.cn/problems/count-good-triplets/solutions/371340/tong-ji-hao-san-yuan-zu-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
- 复杂度分析:
- 时间复杂度: O ( n 2 + n S ) O(n^2+nS) O(n2+nS),其中 n n n 是数组 a r r arr arr 的长度, S S S 为数组的值域上限,这里为 1000 1000 1000。
- 空间复杂度: O ( S ) O(S) O(S)。我们需要 O ( S ) O(S) O(S) 的空间维护 a r r [ i ] arr[i] arr[i] 频次数组的前缀和。
链接:力扣本题官方题解
来源:力扣(LeetCode)
相关文章:
)
力扣每日打卡 1534. 统计好三元组 (简单)
力扣 1534. 统计好三元组 简单 前言一、题目内容二、解题方法1. 暴力解法2.官方题解2.1 方法一:枚举2.2 方法二:枚举优化 前言 这是刷算法题的第十二天,用到的语言是JS 题目:力扣 1534. 统计好三元组 (简单) 一、题目内容 给你一…...

《Vue3学习手记2》
今天主要学习Vue3中的数据监视: ps: 代码中的注释写的很详细,这样更有利于理解 watch 作用: 监视数据的变化(和Vue2中watch作用一致) 特点: Vue3中的watch只能监视以下四种数据: ref创建定义的数据(基本类型、对象类型)reactiv…...

在pycharm中搭建yolo11分类检测系统1--PyQt5学习(一)
实验条件:pycharm24.3autodlyolov11环境PyQt5 如果pycharm还没有配PyQt5的话就先去看我原先写的这篇博文: PyQT5安装搭配QT DesignerPycharm)-CSDN博客 跟练参考文章: 目标检测系列(四)利用pyqt5实现yo…...

【经验记录贴】使用配置文件提高项目的可维护性
mark一下。 整体修改前后如下: 课题: 在项目中有一个支持的文件类型的FILE_TYPE的定义, 这个是写死在主程序中,每次增加可以支持的文件类型的时候,都需要去修改主程序中这个FILGE_TYPE的定义。 主程序修改其实不太花时…...

从JSON到SQL:基于业务场景的SQL生成器实战
引言 在数据驱动的业务场景中,将业务需求快速转化为SQL查询是常见需求。本文将通过一个轻量级的sql_json_to_sql函数,展示如何将JSON格式的查询描述转换为标准SQL语句,并结合实际业务场景验证其功能。 核心代码解析 1. 代码实现 def sql_j…...

空格键会提交表单吗?HTML与JavaScript中的行为解析
在网页开发中,理解用户交互细节对于提供流畅的用户体验至关重要。一个常见的问题是:空格键是否会触发表单提交?本文将通过一个简单的示例解释这一行为,并探讨如何使用HTML和JavaScript来定制这种交互。 示例概览 考虑以下HTML代…...
)
06 - 多线程-JUC并发编程-原子类(二)
上一章,讲解java (java.util.concurrent.atomic) 包中的 支持基本数据类型的原子类,以及支持数组类型的原子类,这一章继续讲解支持对实体类的原子类,以及原子类型的修改器。 还有最后java (java…...

vue3 实现谷歌登录
很多人都是直接在 index.html 文件中引入的,刚开始我也那样写但是谷歌的api只能调起一次后续就不会生效了 我的登录是个弹窗,写在app.vue 文件中 const isGoogleLoaded ref(true);onMounted(async () > {initialize(); }); // 初始化 const initi…...

SOME/IP中”客户端消费“及”服务端提供”的解析
先上结论 AREthAddConsumedEventGroup-->客户端的函数-->谁调用 Consumed函数,谁就是消费者 AREthAddProvidedEventGroup-->服务端的函数-->谁调用 Provided函数,谁就是服务端 Server 端:AREthAddProvidedEventGroup → 声明 &…...
)
GO语言入门:字符串处理1(打印与格式化输出)
13.1 打印文本 在 fmt 包中,Print 函数用于打印(输出)文本信息。依据输出目标的不同,Print 函数可以划分为三组,详见下表。 按应用目标分组函数说明将文本信息输出到标准输出流,一般是输出到屏幕上Print将…...

Linux 深入浅出信号量:从线程到进程的同步与互斥实战指南
知识点1【信号量概述】 信号量是广泛用于进程和线程间的同步和互斥。信号量的本质 是一个非负的整数计数器,它被用来控制对公共资源的访问 当信号量值大于0的时候,可以访问,否则将阻塞。 PV原语对信号量的操作,一次P操作使信号…...

Oracle数据库数据编程SQL<9.1 数据库逻辑备份和迁移exp和imp之导出、导入>
EXP (Export) 和 IMP (Import) 是 Oracle 提供的传统数据导出导入工具,用于数据库逻辑备份和迁移。尽管在较新版本中已被 Data Pump (EXPDP/IMPDP) 取代,但在某些场景下仍然有用。 目录 一、EXP 导出工具 1. 基本语法 2. 常用参数说明 3. 导出模式 3.1 表模式导出 3.2 用…...

DotnetCore开源库SampleAdmin源码编译
1.报错: System.Net.Sockets.SocketException HResult0x80004005 Message由于目标计算机积极拒绝,无法连接。 SourceSystem.Net.Sockets StackTrace: 在 System.Net.Sockets.Socket.AwaitableSocketAsyncEventArgs.ThrowException(SocketError error, C…...
)
Kaggle-Disaster Tweets-(二分类+NLP+模型融合)
Disaster Tweets 题意: 就是给出一个dataframe包含text这一列代表着文本,文本会有一些词,问对于每条记录中的text是真关于灾难的还是假关于灾难的。 比如我们说今天作业真多,这真是一场灾难。实际上这个灾难只是我们调侃而言的。…...

搭建一个网站需要选择什么配置的服务器?
一般要考虑网站规模、技术需求等因素来进行选择。 小型网站:个人博客、小型企业官网等日均量在 1000 以内的网站,一般推荐2 核 CPU、4GB 内存、50GB 硬盘,带宽 1 - 5M。如果是纯文字内容且图片较少的小型网站,初始阶段 1 核 CPU、…...

idea如何使用git
在 IntelliJ IDEA 中使用 Git 的详细步骤如下,分为配置、基础操作和高级功能,适合新手快速上手: 一、配置 Git 安装 Git 下载并安装 Git,安装时勾选“Add to PATH”。验证安装:终端输入 git --version 显示版本…...

webpack vite
1、webpack webpack打包工具(重点在于配置和使用,原理并不高优。只在开发环境应用,不在线上环境运行),压缩整合代码,让网页加载更快。 前端代码为什么要进行构建和打包? 体积更好&#x…...

.Net 9 webapi使用Docker部署到Linux
参考文章连接: https://www.cnblogs.com/kong-ming/p/16278109.html .Net 6.0 WebApi 使用Docker部署到Linux系统CentOS 7 - 长白山 - 博客园 项目需要跨平台部署,所以就研究了一下菜鸟如何入门Net跨平台部署,演示使用的是Net 9 webAPi Li…...

PyTorch 根据官网命令行无法安装 GPU 版本 解决办法
最近遇到一个问题,PyTorch 官网给出了 GPU 版本的安装命令,但安装成功后查看版本,仍然是 torch 2.6.0cpu 1. 清理现有 PyTorch 安装 经过探索发现,需要同时卸载 conda 和 pip 安装的 torch。 conda remove pytorch torchvision …...

PHP防火墙代码,防火墙,网站防火墙,WAF防火墙,PHP防火墙大全
PHP防火墙代码,防火墙,网站防火墙,WAF防火墙,PHP防火墙大全 资源宝整理分享:https://www.htple.net PHP防火墙(作者:悠悠楠杉) 验证测试,链接后面加上?verify_cs1后可以自行测试 <?php //复制保存zzwaf.php$we…...
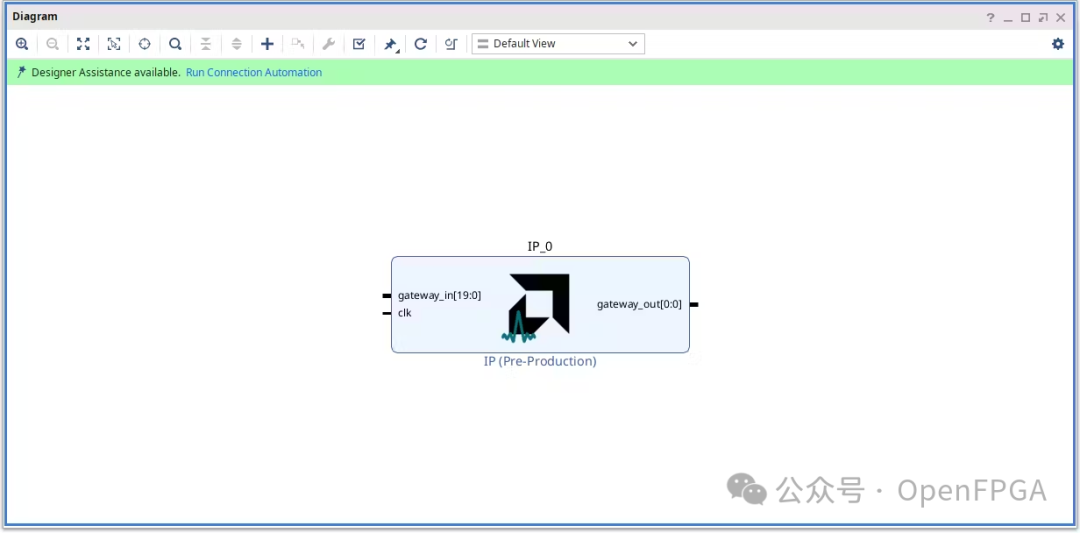
使用 Vitis Model Composer 生成 FPGA IP 核
本文将逐步介绍如何使用 Vitis Model Composer 生成 FPGA IP 核,从建模到部署。 在当今快节奏的世界里,技术正以前所未有的速度发展,FPGA 设计也不例外。高级工具层出不穷,加速着开发进程。传统上,FPGA 设计需要使用硬…...

Day08 【基于jieba分词实现词嵌入的文本多分类】
基于jieba分词的文本多分类 目标数据准备参数配置数据处理模型构建主程序测试与评估测试结果 目标 本文基于给定的词表,将输入的文本基于jieba分词分割为若干个词,然后将词基于词表进行初步编码,之后经过网络层,输出在已知类别标…...

BERT、T5、ViT 和 GPT-3 架构概述及代表性应用
BERT、T5、ViT 和 GPT-3 架构概述 1. BERT(Bidirectional Encoder Representations from Transformers) 架构特点 基于 Transformer 编码器:BERT 使用多层双向 Transformer 编码器,能够同时捕捉输入序列中每个词的左右上下文信息…...

倚光科技:以创新之光,雕琢全球领先光学设计公司
在光学技术飞速发展的当下,每一次突破都可能为众多领域带来变革性的影响。而倚光(深圳)科技有限公司,作为光学设计公司的一颗璀璨之星,正以其卓越的创新能力和深厚的技术底蕴,引领着光学设计行业的发展潮流…...

数据结构(六)——红黑树及模拟实现
目录 前言 红黑树的概念及性质 红黑树的效率 红黑树的结构 红黑树的插入 变色不旋转 单旋变色 双旋变色 插入代码如下所示: 红黑树的查找 红黑树的验证 红黑树代码如下所示: 小结 前言 在前面的文章我们介绍了AVL这一棵完全二叉搜索树&…...
】家政平台安全“攻防战”:渗透测试全解析)
【家政平台开发(48)】家政平台安全“攻防战”:渗透测试全解析
本【家政平台开发】专栏聚焦家政平台从 0 到 1 的全流程打造。从前期需求分析,剖析家政行业现状、挖掘用户需求与梳理功能要点,到系统设计阶段的架构选型、数据库构建,再到开发阶段各模块逐一实现。涵盖移动与 PC 端设计、接口开发及性能优化,测试阶段多维度保障平台质量,…...

Python爬虫-爬取全球股市涨跌幅和涨跌额数据
前言 本文是该专栏的第52篇,后面会持续分享python爬虫干货知识,记得关注。 本文中,笔者将基于Python爬虫,实现批量采集全球股市行情(亚洲,美洲,欧非,其他等)的各股市“涨跌幅”以及“涨跌额”数据。 具体实现思路和详细逻辑,笔者将在正文结合完整代码进行详细介绍。…...

解决 Vue 中 input 输入框被赋值后,无法再修改和编辑的问题
目录 需求: 出现 BUG: Bug 代码复现 解决问题: 解决方法1: 解决方法2 关于 $set() 的补充: 需求: 前段时间,接到了一个需求:在选择框中选中某个下拉菜单时,对应的…...

【差分隐私相关概念】瑞丽差分隐私(RDP)-瑞丽散度约束了贝叶斯因子后验变化
分步解释和答案: 在Rnyi差分隐私(RDP)框架中,通过贝叶斯因子和Rnyi散度的关系可以推导出关于后验变化的概率保证。以下是关键步骤的详细解释: 1. 贝叶斯因子的定义与分解 设相邻数据集 D D D 和 D ′ D D′&#x…...

vue3 onMounted 使用方法和注意事项
基础用法 / 语法糖写法 <script> import { onMounted } from vue;// 选项式 API 写法 export default {setup() {onMounted(() > {console.log(组件已挂载);});} } </script><script setup> onMounted(() > {console.log(组件已挂载); }); </scrip…...
