有哪些哲学流派适合创业二
好的,让我们更深入地探讨如何将哲学与数学深度融合,构建一套可落地的创业操作系统。以下从认知框架、决策引擎、执行算法三个维度展开,包含具体工具和黑箱拆解:
一、认知框架:用哲学重构商业本质
1. 本体论级问题拆解(Ontology)
- 海德格尔式发问:
传统问法:"如何做一个更好的电商平台?"
哲学重构:"'在线交易'的存在方式是什么?" → 答案可能是"信任的数字化具象",由此衍生出区块链电商或小红书式社区验证。 - 数学表达:用集合论定义市场边界
Market={Userneed∣∃Solutiontech∩Viableeconomy}Market = \{ User_{need} \mid \exists Solution_{tech} \cap Viable_{economy} \}Market={Userneed∣∃Solutiontech∩Viableeconomy}
2. 现象学还原(Phenomenological Reduction)
- 胡塞尔"悬置判断"实践:
观察用户时不依赖现有行业报告,而是记录100个原始行为片段(如抖音早期发现"用户滑动手指快于预期"),用拓扑学建模行为空间:
Behaviorspace=∫t0t1(Attentionfocus×Musclememory) dtBehavior_{space} = \int_{t_0}^{t_1} (Attention_{focus} \times Muscle_{memory}) \, dtBehaviorspace=∫t0t1(Attentionfocus×Musclememory)dt
3. 辩证法冲突挖掘
- 矛盾矩阵构建:
正题(现状) 反题(痛点) 合题(机会) 外卖准时 骑手安全风险 无人配送+保险金融 数据支撑:用卡方检验验证矛盾显著性(χ2>3.84\chi^2 > 3.84χ2>3.84时值得解决)
二、决策引擎:数学化的哲学实践
1. 贝叶斯主义认知升级
- 公式:
P(H∣E)=P(E∣H)⋅P(H)P(E)P(H|E) = \frac{P(E|H) \cdot P(H)}{P(E)}P(H∣E)=P(E)P(E∣H)⋅P(H) - 应用场景:
- 先验概率P(H)P(H)P(H):行业基准成功率(如 SaaS 企业 5%)
- 似然率P(E∣H)P(E|H)P(E∣H):用户访谈中3/10提及痛点→调整假设
- 哲学约束:避免"观察者效应",用哥德尔不完备定理提醒自己"总有数据不可见"
2. 博弈论行动策略
- 支付矩阵设计(以社区团购为例):
| | 对手降价 | 对手维持 |
|---|---|---|
| 我降价 | (-5,-5) | (15,-10) |
| 我增值 | (-10,12) | (20,20) | - 纳什均衡解:当Marginalcost<LearningrateMarginal_{cost} < Learning_{rate}Marginalcost<Learningrate时选择增值服务
3. 拓扑学增长模型
- 关键定义:将用户关系网视为拓扑空间,找到"同胚不变性"(如微信的强连接 vs 抖音的弱连接)
- 不变量计算:
Eulercharacteristic=Vertices−Edges+FacesEuler_{characteristic} = Vertices - Edges + FacesEulercharacteristic=Vertices−Edges+Faces
应用:当χ>0\chi > 0χ>0时适合做社交裂变,χ<0\chi < 0χ<0时适合内容推荐
三、执行算法:从形而上到代码
1. 存在主义OKR系统
- 目标层(Being):用萨特"自在-自为"定义阶段目标
- 种子期:自在存在(解决明确痛点)
- 增长期:自为存在(创造新需求)
- 关键结果(KR):
KRexistential=∑i=1nValidatedassumptionsTotalassumptions≥70%KR_{existential} = \frac{\sum_{i=1}^{n} Validated_{assumptions}}{Total_{assumptions}} \geq 70\%KRexistential=Totalassumptions∑i=1nValidatedassumptions≥70%
2. 控制论反馈循环
pythonCopy Code# 哲学约束下的PID控制器
def startup_PID(error, prev_error):Kp = 0.6 # 实用主义系数(快速响应)Ki = 0.2 # 第一性原理系数(本质修正) Kd = 0.2 # 辩证法系数(矛盾调节)
adjustment = Kp*error + Ki*integral(error) + Kd*(error - prev_error)
<span class="hljs-keyword">return</span> adjustment <span class="hljs-keyword">if</span> adjustment < Stoic_threshold <span class="hljs-keyword">else</span> pivot()
3. 混沌工程管理
- 李雅普诺夫指数计算:
λ=limt→∞1tln∣δZ(t)δZ(0)∣\lambda = \lim_{t \to \infty} \frac{1}{t} \ln \left| \frac{\delta Z(t)}{\delta Z(0)} \right|λ=limt→∞t1ln δZ(0)δZ(t) - 应用:当λ>0\lambda > 0λ>0时(如用户增长突变),启动"尼采超预案":
- 预留20%资源应对不确定性
- 用非欧几何重新设计组织架构(去中心化节点)
四、验证案例:特斯拉的哲学数学化
-
本体论攻击:
- 哲学问题:"能源"的本质是"电子流动+信息控制" → 数学建模:
∇⋅E=ρε0⇒Superchargernetwork\nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0} \quad \Rightarrow \quad Supercharger_{network}∇⋅E=ε0ρ⇒Superchargernetwork
- 哲学问题:"能源"的本质是"电子流动+信息控制" → 数学建模:
-
反脆弱证明:
- 用概率论计算电池爆炸风险<10−9<10^{-9}<10−9次/年
- 哲学对冲:用克尔凯郭尔"信仰的飞跃"说服早期用户
-
拓扑增长:
- 将车主关系网定义为R3\mathbb{R}^3R3中的纤维丛,通过OTA更新实现"连续变形"
五、创业者每日训练清单
-
晨间思辨(10分钟):
- 用哥德尔编码法将昨日问题转化为数学命题
- 施加一个哲学约束(如"康德绝对命令")重新思考
-
决策沙盘(工具推荐):
- 用Wolfram Alpha跑符号计算验证商业假设
- 在Leibniz可能世界理论中模拟不同策略
-
夜间复盘:
Reflectionscore=Philosophicalrigor×MathematicalprecisionCognitivebiasReflection_{score} = \frac{Philosophical_{rigor} \times Mathematical_{precision}}{Cognitive_{bias}}Reflectionscore=CognitivebiasPhilosophicalrigor×Mathematicalprecision
当Score<1Score < 1Score<1时触发"笛卡尔式怀疑"重置
这套系统本质是用数学确保哲学不沦为鸡汤,用哲学防止数学陷入局部最优。当你能用范畴论解释用户心智,用存在主义定义增长极限时,就进入了创业的"物自体"境界——这或许就是贝佐斯说的"固执的愿景,灵活的细节"。
相关文章:

有哪些哲学流派适合创业二
好的,让我们更深入地探讨如何将哲学与数学深度融合,构建一套可落地的创业操作系统。以下从认知框架、决策引擎、执行算法三个维度展开,包含具体工具和黑箱拆解: 一、认知框架:用哲学重构商业本质 1. 本体…...

【Web API系列】Web Shared Storage API之WorkletSharedStorage深度解析与实践指南
前言 在现代Web开发领域,数据存储与隐私保护的矛盾始终存在。传统存储方案如LocalStorage和Cookies面临着日益严格的安全限制,而跨域数据共享的需求却在持续增长。正是在这样的背景下,Web Shared Storage API应运而生,其核心组件…...

UE5 制作方块边缘渐变边框效果
该效果基于之前做的(https://blog.csdn.net/grayrail/article/details/144546427)进行修改得到,思路也很简单: 1.打开实时预览 1.为了制作时每个细节调整方便,勾选Live Update中的三个选项,开启实时预览。…...

MyBatis 如何使用
1. 环境准备 添加依赖(Maven) 在 pom.xml 中添加 MyBatis 和数据库驱动依赖: <dependencies><!-- MyBatis 核心库 --><dependency><groupId>org.mybatis</groupId><artifactId>mybatis</artifactId&g…...

【MySQL】索引分类、聚簇与非聚簇索引,索引优化,常见explain分析索引案例,type字段
索引基本概念 索引是数据库中用于加速数据检索的数据结构,类似于书籍的目录。它通过建立额外的数据结构来存储部分数据,从而加快查询速度。 索引的优缺点 优点缺点加快数据检索速度占用额外存储空间保证数据唯一性(唯一索引)插…...

MySQL Binlog 数据恢复总结
🌲 总入口:你想恢复什么? 恢复类型 ├── 表结构 表数据(整张表被 DROP) │ ├── Binlog 中包含 CREATE TABLE │ │ └── ✅ 直接用 mysqlbinlog 提取建表 数据语句,回放即可 │ └── B…...

STM32 HAL库内部 Flash 读写实现
一、STM32F407 内部 Flash 概述 1.1 Flash 存储器的基本概念 Flash 存储器是一种非易失性存储器,它可以在掉电的情况下保持数据。STM32F407 系列微控制器内部集成了一定容量的 Flash 存储器,用于存储程序代码和数据。Flash 存储器具有擦除和编程次数的…...

2.3 Spark运行架构与流程
Spark运行架构与流程包括几个核心概念:Driver负责提交应用并初始化作业,Executor在工作节点上执行任务,作业是一系列计算任务,任务是作业的基本执行单元,阶段是一组并行任务。Spark支持多种运行模式,包括单…...

Redisson分布式锁全攻略:用法、场景与要点
目录 1. 普通可重入锁(RLock) 2. 公平锁(RFairLock) 3. 读写锁(RReadWriteLock) 4. 多重锁(RedissonMultiLock) 1. 普通可重入锁(RLock) import org.redisson.Redisson; import org.redisson.api.RLoc…...

软件测试——BUG概念
目录 一、软件测试生命周期 二、BUG 2.1BUG概念 2.2BUG要素 2.3BUG级别 2.4 BUG的生命周期 2.5测试人员与开发人员因为BUG发生争执 2.6BUG评审 一、软件测试生命周期 软件测试贯穿于软件的整个生命周期 软件测试的生命周期指测试流程,每个阶段有不同的目标…...

二、Android Studio环境安装
一、下载安装 下载 Android Studio 和应用工具 - Android 开发者 | Android DevelopersAndroid Studio 提供了一些应用构建器以及一个已针对 Android 应用进行优化的集成式开发环境 (IDE)。立即下载 Android Studio。https://developer.android.google.cn/studio?hlzh-c…...

Hyperlane:重新定义Rust Web开发的未来 [特殊字符][特殊字符]
Hyperlane:重新定义Rust Web开发的未来 🚀🔥 大家好!👋 今天我要向各位技术爱好者介绍一个令人兴奋的Rust HTTP服务器库——Hyperlane 🌟。作为一个轻量级、高性能的框架,Hyperlane正在悄然改变…...

从零构建机器学习流水线:Dagster+PyTorch实战指南
本文将系统讲解机器学习流水线的核心原理,并通过Dagster编排框架与PyTorch深度学习库的实战结合,手把手演示从数据预处理到生产部署的全流程。文中包含可运行的代码示例、最佳实践和性能对比分析,帮助开发者快速构建可扩展、易维护的机器学习…...

RabbitMQ架构原理及消息分发机制
RabbitMQ架构原理及消息分发机制 在现代分布式系统中,消息队列是不可或缺的组件之一。它不仅能够解耦系统模块,还能实现异步通信和削峰填谷。在众多消息队列中,RabbitMQ 因其高并发、高可靠性和丰富的功能而备受青睐。本文将从 RabbitMQ 的基…...

React 项目src文件结构
SCSS 组件库 SCSS为预处理器 支持除原生CSS外的其他语句 别名路径 在项目下的第一级目录就加入craco.config.js文件并且修改packpage.js 中的部分 // 扩展webpage的配置const path require(path)module.exports {// exports配置webpack:{// 配置别名alias:{:path.resolve(__d…...

Redis --- 基本数据类型
Redis --- 基本数据类型 Redis Intro5种基础数据类型 Redis Intro Redis(Remote Dictionary Server)是一款开源的高性能键值存储系统,常用于缓存、消息中间件和实时数据处理场景。以下是其核心特点、数据类型及典型使用场景: 核心…...

React 高级特性与最佳实践
在掌握了 React 的基础知识后,我们可以进一步探索 React 的高级特性和最佳实践。这些特性将帮助你构建更高效、可维护和可扩展的 React 应用。本文重点介绍 Hooks、Context、Refs 和高阶组件等核心高级特性。 1. Hooks:函数组件的强大工具 Hooks 是 Rea…...

一个由通义千问以及FFmpeg的AVFrame、buffer引起的bug:前面几帧影响后面帧数据
目录 1 问题描述 2 我最开始的代码----错误代码 3 正确的代码 4 为什么前面帧的结果会叠加到了后面帧上----因为ffmpeg新一帧只更新上一帧变化的部分 5 以后不要用通义千问写代码 1 问题描述 某个项目中,需要做人脸马赛克,然后这个是君正的某款芯片…...

12.第二阶段x64游戏实战-远程调试
免责声明:内容仅供学习参考,请合法利用知识,禁止进行违法犯罪活动! 本次游戏没法给 内容参考于:微尘网络安全 上一个内容:11.第二阶段x64游戏实战-框架代码细节优化 本次写的内容是关于调试、排错相关的…...

Coze 和 n8n 的详细介绍及多维度对比分析,涵盖功能、架构、适用场景、成本等关键指标
以下是 Coze 和 n8n 的详细介绍及多维度对比分析,涵盖功能、架构、适用场景、成本等关键指标: 一、Coze 详细介绍 1. 基础信息 类型:低代码自动化平台(SaaS)。开源性:闭源(企业版需付费&…...

咋用fliki的AI生成各类视频?AI生成视频教程
最近想制作视频,多方考查了决定用fliki,于是订阅了一年试试,这个AI生成的视频效果来看真是不错,感兴趣的自己官网注册个账号体验一下就知道了。 fliki官网 Fliki生成视频教程 创建账户并登录 首先,访问fliki官网并注…...

【NLP】 20. Attention 和 self-attention
1. 背景与基本概念 1.1 编码器-解码器模型的瓶颈问题 传统的序列到序列(Seq2Seq)模型主要依靠编码器生成单一固定长度的上下文向量,然后由解码器逐步生成输出。这个过程存在两个主要问题: 瓶颈问题:固定…...

vue3+element-plus实现省市区三级地址多选
目录 背景实现功能点遗留问题完整代码参考 背景 需要实现:选择省级地址时,回传节点为 [ 省级地址 id], 选择市级地址时,回传节点为 [ 省级地址 id,市级地址 id], 选择区县地址时,回传节点为 [ …...

centos部署的openstack发布windows虚拟机
CentOS上部署的OpenStack可以发布Windows虚拟机。在CentOS上部署OpenStack后,可以通过OpenStack平台创建和管理Windows虚拟机。以下是具体的步骤和注意事项: 安装和配置OpenStack: 首先,确保系统满足OpenStack的最低硬件…...

Linux : 进程等待以及进程终止
进程控制之进程等待 (一)fork函数1*fork函数返回值2.父子进程的写时拷贝 (二)进程终止1.进程退出码2.进程常见退出方法(1)_exit(2)exit(3)return 3.进程的异常…...

LSTM结合LightGBM高纬时序预测
1. LSTM 时间序列预测 LSTM 是 RNN(Recurrent Neural Network)的一种变体,它解决了普通 RNN 训练时的梯度消失和梯度爆炸问题,适用于长期依赖的时间序列建模。 LSTM 结构 LSTM 由 输入门(Input Gate)、遗…...

详细解释MCP项目中安装命令 bunx 和 npx区别
详细解释 bunx 和 npx 1. bunx bunx 是 Bun 的一个命令行工具,用于自动安装和运行来自 npm 的包。它是 Bun 生态系统中类似于 npx 或 yarn dlx 的工具。以下是 bunx 的主要特点和使用方法: 自动安装和运行: bunx 会自动从 npm 安装所需的包…...
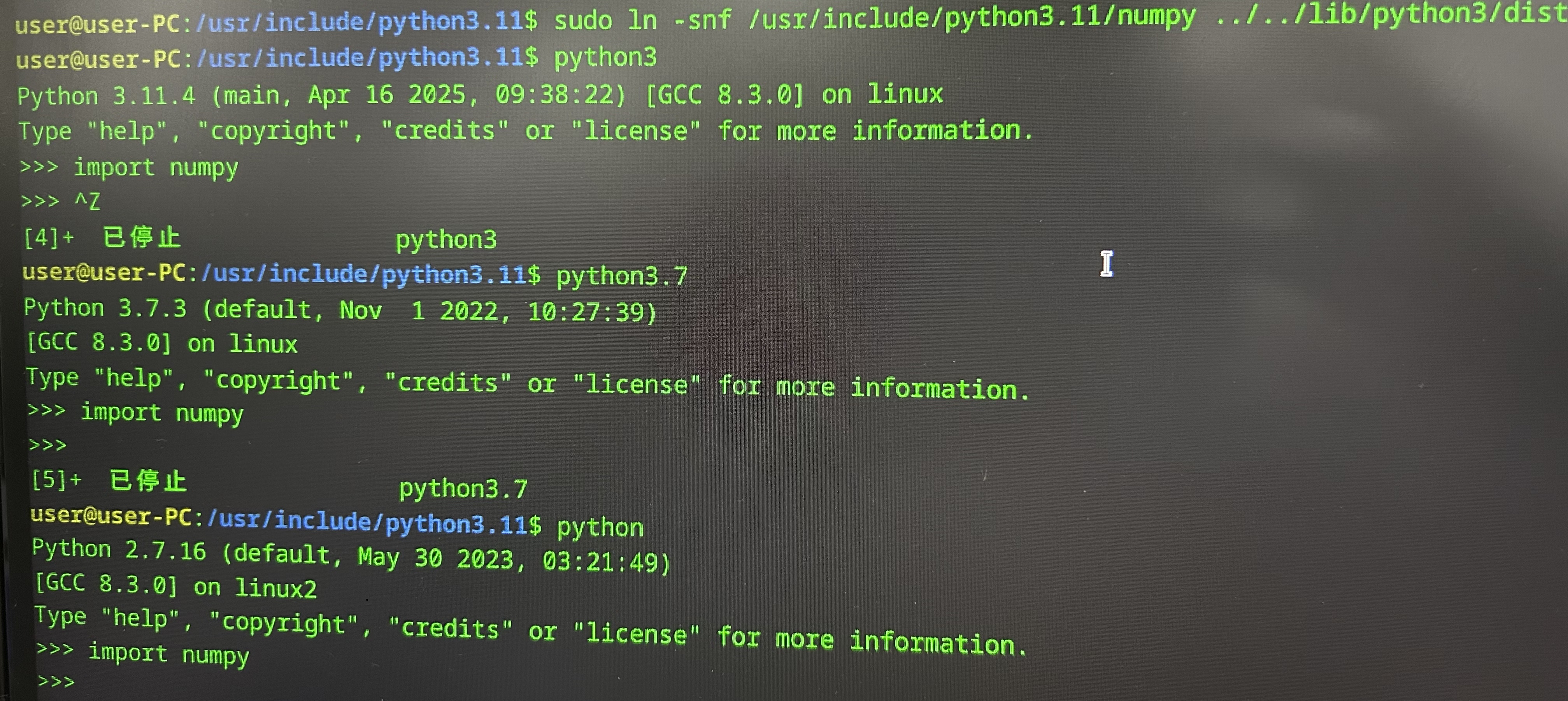
【统信UOS操作系统】python3.11安装numpy库及导入问题解决
一、安装Python3.11.4 首先来安装Python3.11.4。所用操作系统:统信UOS 前提是准备好Python3.11.4的安装包(可从官网下载(链接)),并解压到本地: 右键,选择“在终端中打开”ÿ…...

【中间件】nginx反向代理实操
一、说明 nginx用于做反向代理,其目标是将浏览器中的请求进行转发,应用场景如下: 说明: 1、用户在浏览器中发送请求 2、nginx监听到浏览器中的请求时,将该请求转发到网关 3、网关再将请求转发至对应服务 二、具体操作…...

嵌入式硬件篇---加法减法积分微分器
文章目录 前言1. 加法器(Summing Amplifier)结构反相加法器同相加法器 特点反相输出虚地特性 应用 2. 减法器(差分放大器)结构特点差分放大共模抑制比 应用 3. 积分器结构特点直流漂移问题应用 4. 微分器结构特点应用关键注意事项…...
