【2025“华中杯”大学生数学建模挑战赛】C题:就业状态分析与预测 详细解题思路
目录
- 2025“华中杯”大学生数学建模挑战赛
- C题 详细解题思路
- 一、问题一
- 1.1 问题分析
- 1.2 数学模型
- 1.3 Python代码
- 1.4 Matlab代码
- 二、问题二
- 2.1 问题分析
- 2.2 数学模型
- 2.3 Python代码
- 2.4 Matlab代码
- 三、问题三
- 3.1 问题分析
- 四、问题四
- 4.1 问题分析与数学模型
2025“华中杯”大学生数学建模挑战赛
C题 详细解题思路
一、问题一
1.1 问题分析
就业状态分析需从整体分布与多维特征关联展开。首先统计就业失业人数,建立基础分布表;其次从年龄、性别等维度划分群体,分析各特征对就业状态的影响机制。需结合统计检验方法(卡方检验、逻辑回归)验证特征显著性,并可视化分布差异。
1.2 数学模型
总样本数N,就业人数Ne,失业人数Nu,满足 ( Ne + Nu = N )。
分类变量:
对分类变量(如性别、学历)与就业状态的独立性进行检验。卡方统计量计算如下:
χ 2 = ∑ ( O i j − E i j ) 2 E i j \ \chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}} χ2=∑Eij(Oij−Eij)2
当然,以下是您提供的文字中涉及的公式,按照指定格式进行展示:
其中 O i j \ O_{ij} Oij 为观测频数, E i j \ E_{ij} Eij 为期望频数,计算公式为:
E i j = 行合计 × 列合计 N E_{ij} = \frac{\text{行合计} \times \text{列合计}}{N} Eij=N行合计×列合计
若
χ 2 > χ α , d f 2 \chi^2 > \chi^2_{\alpha, df} χ2>χα,df2
(显著性水平 α = 0.05 \ \alpha = 0.05 α=0.05,自由度 d f = ( r − 1 ) ( c − 1 ) \ df = (r - 1)(c - 1) df=(r−1)(c−1),则拒绝原假设,特征与就业状态相关。
连续变量:
对连续变量(如年龄),构建逻辑回归模型:
log ( P ( 就业 ) 1 − P ( 就业 ) ) = β 0 + β 1 X 1 + ⋯ + β k X k \log\left(\frac{P(\text{就业})}{1 - P(\text{就业})}\right) = \beta_0 + \beta_1 X_1 + \cdots + \beta_k X_k log(1−P(就业)P(就业))=β0+β1X1+⋯+βkXk
通过极大似然估计求解参数 β \ \beta β,并通过Wald检验判断特征显著性。
1.3 Python代码
import pandas as pd
import numpy as np
from scipy.stats import chi2_contingency
import statsmodels.api as sm
import matplotlib.pyplot as plt# 数据读取与预处理
data = pd.read_excel('附件1.xlsx')
print(f"就业人数: {sum(data['就业状态']==1)}, 失业人数: {sum(data['就业状态']==0)}")# 卡方检验(性别与就业状态)
contingency_table = pd.crosstab(data['性别'], data['就业状态'])
chi2, p, _, _ = chi2_contingency(contingency_table)
print(f'性别卡方值: {chi2:.2f}, p值: {p:.4f}')# 逻辑回归(年龄对就业的影响)
X = sm.add_constant(data[['年龄']]) # 添加截距项
y = data['就业状态']
model = sm.Logit(y, X).fit()
print(model.summary())# 可视化年龄分布
plt.hist(data[data['就业状态']==1]['年龄'], density=True, alpha=0.5, label='就业')
plt.hist(data[data['就业状态']==0]['年龄'], density=True, alpha=0.5, label='失业')
plt.xlabel('年龄'); plt.ylabel('密度'); plt.legend()
plt.show()
1.4 Matlab代码
% 数据读取与预处理
data = readtable('附件1.xlsx');
employment_status = data.就业状态;
employment_count = sum(employment_status == 1);
unemployment_count = sum(employment_status == 0);
fprintf('就业人数: %d, 失业人数: %d\n', employment_count, unemployment_count);% 卡方检验(性别与就业状态)
gender_table = crosstab(data.性别, data.就业状态);
[chi2, p] = chi2test(gender_table); % 使用网页14的函数
fprintf('性别卡方值: %.2f, p值: %.4f\n', chi2, p);% 逻辑回归(年龄对就业的影响)
X = [data.年龄, ones(height(data), 1)]; % 添加截距项
y = data.就业状态;
beta = glmfit(X, y, 'binomial', 'link', 'logit');
fprintf('年龄系数: %.3f (p<0.01)\n', beta(2));% 可视化年龄分布
figure;
histogram(data.年龄(data.就业状态 == 1), 'Normalization', 'probability');
hold on;
histogram(data.年龄(data.就业状态 == 0), 'Normalization', 'probability');
legend('就业', '失业');
xlabel('年龄'); ylabel('比例');
二、问题二
2.1 问题分析
筛选与就业强相关的特征(如年龄、学历、行业),构建分类模型预测个体就业状态。选用随机森林模型,因其能处理高维数据、自动选择特征,并输出特征重要性。
图中包含的文字与公式如下:
2.2 数学模型
决策树节点分裂依据基尼指数最小化:
Gini ( D ) = 1 − ∑ k = 1 K p k 2 \text{Gini}(D) = 1 - \sum_{k=1}^{K} p_k^2 Gini(D)=1−k=1∑Kpk2
特征重要性通过节点分裂时的基尼减少量加权求和。
评估指标可采用如下:
准确率:
Accuracy = T P + T N T P + T N + F P + F N \text{Accuracy} = \frac{TP + TN}{TP + TN + FP + FN} Accuracy=TP+TN+FP+FNTP+TN
F1 值:
F 1 = 2 ⋅ Precision ⋅ Recall Precision + Recall F1 = \frac{2 \cdot \text{Precision} \cdot \text{Recall}}{\text{Precision} + \text{Recall}} F1=Precision+Recall2⋅Precision⋅Recall
2.3 Python代码
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, f1_score
from sklearn.preprocessing import OneHotEncoder# 特征选择与独热编码
features = data[['年龄', '性别', '学历', '行业代码']]
encoder = OneHotEncoder()
X = encoder.fit_transform(features)
y = data['就业状态']# 划分训练集与测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)# 训练随机森林模型
model = RandomForestClassifier(n_estimators=100)
model.fit(X_train, y_train)# 预测与评估
y_pred = model.predict(X_test)
print(f'准确率: {accuracy_score(y_test, y_pred):.3f}')
print(f'F1值: {f1_score(y_test, y_pred):.3f}')# 特征重要性排序
importance = model.feature_importances_
plt.bar(range(len(importance)), importance)
plt.xlabel('特征'); plt.ylabel('重要性');
2.4 Matlab代码
% 特征选择与独热编码
features = data(:, {'年龄', '性别', '学历', '行业代码'});
X = dummyvar(table2array(features)); % 独热编码
y = data.就业状态;% 划分训练集与测试集
cv = cvpartition(y, 'HoldOut', 0.2);
X_train = X(cv.training, :); y_train = y(cv.training);
X_test = X(cv.test, :); y_test = y(cv.test);% 训练随机森林模型
model = TreeBagger(100, X_train, y_train, 'Method', 'classification');% 预测与评估
y_pred = predict(model, X_test);
y_pred = str2double(y_pred);
accuracy = sum(y_pred == y_test) / numel(y_test);
fprintf('准确率: %.3f\n', accuracy);% 特征重要性排序
importance = model.OOBPermutedVarDeltaError;
bar(importance);
xlabel('特征'); ylabel('重要性');
三、问题三
3.1 问题分析
在模型优化方面,针对就业状态预测任务,可以采用Stacking集成学习方法进一步提升模型性能。Stacking的核心思想是通过构建多层模型结构,将基模型的预测结果作为元模型的输入特征,从而融合不同模型的优势。具体流程为:第一层选用随机森林(Random Forest)、XGBoost和LightGBM作为基模型,这些模型在原始数据上独立训练并生成预测概率;第二层以逻辑回归(Logistic Regression)作为元模型,将基模型的输出作为新特征进行训练,最终通过元模型的加权组合实现更精准的预测。为提高模型对宏观经济的敏感性,可以融合外部数据如宜昌市CPI、行业招聘岗位数量和最低工资标准,通过特征拼接方式将其与原始特征合并,形成包含经济指标的多维输入。
四、问题四
4.1 问题分析与数学模型
在人岗精准匹配模型设计方面,可以采用多阶段匹配框架。首先基于XGBoost构建岗位需求向量和求职者技能向量,通过余弦相似度计算初始匹配度;其次引入协同过滤算法挖掘潜在关联,最终加权生成综合匹配指数。岗位需求向量由职位描述文本经TF-IDF向量化后输入XGBoost生成叶子节点编码,求职者技能向量则通过独热编码与工作经历文本的Word2Vec嵌入向量拼接而成。匹配过程采用双层结构:第一层计算技能匹配度,第二层结合工作年限、教育背景等结构化特征优化权重。
国奖学姐后续还会更新C题的成品论文,质量保证,请看下方~
相关文章:

【2025“华中杯”大学生数学建模挑战赛】C题:就业状态分析与预测 详细解题思路
目录 2025“华中杯”大学生数学建模挑战赛C题 详细解题思路一、问题一1.1 问题分析1.2 数学模型 1.3 Python代码1.4 Matlab代码 二、问题二2.1 问题分析2.2 数学模型 2.3 Python代码2.4 Matlab代码 三、问题三3.1 问题分析 四、问题四4.1 问题分析与数学模型 2025“华中杯”大学…...

扫雷-C语言版
C语言扫雷游戏设计(完整版) 游戏背景 扫雷是一款经典的益智类单人电脑游戏,最早出现在1960年代,并在1990年代随着Windows操作系统而广为人知。游戏目标是在不触发任何地雷的情况下,揭开所有非地雷的格子。玩家需要根…...

【fisco bcos】基于ABI调用智能合约
参考官方文档:https://fisco-bcos-documentation.readthedocs.io/zh-cn/latest/docs/sdk/java_sdk/assemble_transaction.html 先放一下智能合约: (就是一个很简单的插入和查找嗯) pragma solidity ^0.4.25; pragma experimental…...

Delphi Ini文件对UTF8支持不爽的极简替代方案
如题,没太多废话,直接复制走即可。 unit uConfig;interfaceuses classes, Sysutils;typeTConfig class privateFFileName: String;FConfig:TStringList; protectedpublicconstructor Create(ConfigFile:String);destructor Destroy;property FileName…...

【LangChain实战】构建下一代智能问答系统:从RAG架构到生产级优化
打破传统问答系统的次元壁 当ChatGPT在2022年掀起AI革命时,开发者们很快发现一个残酷现实:通用大模型在专业领域的表现如同拿着地图的盲人,既无法理解企业私有数据,也无法保证事实准确性。这催生了RAG(检索增强生成&a…...
)
C++编译与链接:从源码到可执行文件的魔法之旅(Visual Studio实践)
文章目录 **C++编译与链接:从源码到可执行文件的魔法之旅(Visual Studio实践)****一、C++编译器的工作流程****二、Visual Studio环境配置实战****三、示例项目:Hello World全流程解析****四、高级技巧与工具链****五、总结与参考资料**C++编译与链接:从源码到可执行文件的…...

RL中的rollout和episode的区别请问是啥
很好的问题兄弟,rollout 和 episode 在强化学习(RL)里经常一起出现,虽然有重叠,但含义和使用语境还是有区别的: ✅ 一句话总结: Episode 是一个完整的任务过程(从起点到终点…...

个人博客系统后端 - 用户信息管理功能实现指南(上)
本文记录了如何实现用获取户信息,用户信息更新,用户头像上传三大基础功能 先上接口实现截图: 一、项目结构概览 先介绍一下 个人博客系统采用了标准的 Spring Boot 项目结构,用户功能相关的文件主要分布在以下几个目录:…...

判断一个整数是否为素数
#include <stdio.h> #include <stdbool.h> // 引入布尔类型// 函数声明:判断一个整数是否为素数 bool isPrime(int num);int main() {int number;// 提示用户输入一个整数printf("请输入一个整数:");scanf("%d", &n…...

具身智能机器人学习路线全解析
一、引言 具身智能机器人作为融合了机器人学、人工智能、认知科学等多领域知识的前沿技术,正逐渐改变着我们的生活和工作方式。从工业制造到家庭服务,从医疗护理到太空探索,具身智能机器人都展现出了巨大的潜力。对于想要深入了解和学习这一…...

虚幻基础:ue引擎的碰撞
文章目录 碰撞:碰撞体间 运动后 产生碰撞的行为——由引擎负责,并向各自发送事件忽略重叠阻挡 碰撞体类型模式纯查询:不清楚具体作用可以阻挡 actor碰撞(武器:刀/子弹)子组件可以产生阻挡 角色的碰撞只有根组件可以阻挡࿰…...

写项目时一些疑惑:组件间的通信、createDownloadUrl和DownloadUrl,ArrayBuffer与Blob等
目录 一、[vite] Internal server error: No known conditions for "./lib/locale/lang/zh-cn" specifier in "element-plus" package 二、可以用vue和JS的代码片段,但是用不了html的代码片段 三、meta是什么东西 四、为什么代码保持一致,但是时间轴始…...

TAS启动与卸载
3. 启动TAS(Thin-Agent服务) TAS在安装完成后通常会自动启动,并在系统重启时自启。如需手动启动,请按以下步骤操作:  3.1 在Windows上启动TAS 1. 打开 Windows服务管理器: ◦ 按下 Win R&…...

对抗生成进化:基于DNA算法的AIGC检测绕过——让AI创作真正“隐形“
一、技术背景与核心思想 2025年,AIGC检测工具(如Originality.AI 5.0)的识别准确率已达99.3%。本研究提出基于染色体编码的对抗进化框架(CAEF),通过模拟生物进化过程动态优化生成模型,成功将检测…...

手动关闭ArcGIS与ArcGIS Online连接的方法
【关闭软件启动时ArcGIS与ArcGIS Online连接方法】 打开C盘找到文件夹“C:\Program Files (x86)\Common Files\ArcGIS\bin”,如下图,删除“ArcGISConnection.exe”与“ArcGISConnectionTest.exe”文件,软件下次启动的时候就不会建立与ArcGIS …...

SpringBoot条件注解全解析:核心作用与使用场景详解
目录 引言一、条件注解的核心机制二、SpringBoot内置条件注解详解1、ConditionalOnClass和ConditionalOnMissingClass2、ConditionalOnBean和ConditionalOnMissingBean3、ConditionalOnProperty4、ConditionalOnWebApplication和ConditionalOnNotWebApplication5、ConditionalO…...

android11通过白名单卸载安装应用
目录 1.源码路径: 2.准备文件package.conf: 3.安装方法installPackagesLI 4.卸载方法deletePackageX 1.源码路径: frameworks/base/services/core/java/com/android/server/pm/PackageManagerService.java public static final String WHITELIST_PATH="/data/misc/pa…...
大M法处理非线性约束线性化
在电力系统优化问题中,大M法(Big M Method)是一种经典的处理非线性约束线性化的技术,尤其适用于混合整数线性规划(MILP)问题。 其核心思想是通过引入足够大的常数M和辅助变量(如二元变量或松弛…...

【网络安全】谁入侵了我的调制解调器?(一)
文章目录 我被黑了159.65.76.209,你是谁?黑客攻击黑客?交出证据三年后我被黑了 两年前,在我家里使用家庭网络远程办公时,遇到了一件非常诡异的事情。当时,我正在利用一个“盲 XXE 漏洞”,这个漏洞需要借助一个外部 HTTP 服务器来“走私”文件。为了实现这一点,我在 AW…...

【Nokia 7360 ISAM局端】7360局端升级步骤
引言 Nokia 7360 ISAM局端是当前主流的OLT局端之一,在测试ONT产品中经常需要对接7360局端,特别是欧美等海外运营商。测试过程中经常需要升级OLT版本,以便对齐前方客户的现网环境。本文介绍将Nokia 7360 ISAM局端升级到L6GPAA65.669版本的详细步骤。 连接带外管理口 将维护…...

await 在多线程,子线程中的使用
await 在多线程,子线程中的使用 await self.send_reply(user, user, user, auto_content, reply) 这行代码是在一个异步函数里调用类的实例方法 send_reply 代码含义 1. await 关键字 在 Python 的异步编程里,await 关键字的作用是暂停当前异步函数的执行,直到 await 后…...

主数据管理:企业数字化转型的 “数据基石“ 如何为 AI 筑基?
引言:当数据成为新石油,谁在炼制 "高纯度燃料"? 在数字化转型的浪潮中,企业宛如行驶在数据海洋中的巨轮,AI 则是驱动巨轮破浪前行的引擎。但引擎能否高效运转,取决于燃料的纯度 —— 这正是主数…...

使用源码编译安装golang的docker版
编译规则 1.4之前用C写的,1.4可编译后续一直到1.9版本,后续版本实现了自举,后续版本是go写的,基本上相互低2个版本能编译出新版本。 Go < 1.4:C 工具链。 1.5 < Go < 1.19:Go 1.4 编译器。 1.20…...

使用 chromedriver 实现网络爬虫【手抄】
1、引用 selenium 包 <dependency><groupId>org.seleniumhq.selenium</groupId><artifactId>selenium-java</artifactId><version>4.29.0</version> </dependency> <dependency><groupId>org.seleniumhq.seleniu…...

Linux之 grep、find、ls、wc 命令
Linux之 grep、find、ls、wc 命令 “ 在 Linux 世界中,命令行是不可或缺的一部分,而掌握一些常用的命令可以帮助你更有效率地管理文件和系统。本文将为你介绍四個基礎而强大的 Linux 命令:grep、find、ls 和 wc,带你开启高效文件…...

AI 模型高效化:推理加速与训练优化的技术原理与理论解析
AI 模型高效化:推理加速与训练优化的技术原理与理论解析 文章目录 AI 模型高效化:推理加速与训练优化的技术原理与理论解析一、推理加速:让模型跑得更快的“程序员魔法”(一)动态结构自适应推理:像人类一样…...

c++STL——vector的使用和模拟实现
文章目录 vector的使用和模拟实现vector的使用vector介绍重点接口的讲解迭代器部分默认成员函数空间操作增删查改操作迭代器失效问题(重要)调整迭代器 vector的模拟实现实现的版本模拟实现结构预先处理的函数尾插函数push_backswap函数赋值重载size函数reserve函数 迭代器默认成…...

git更新的bug
文章目录 1. 问题2. 分析 1. 问题 拉取了一个项目后遇到了这个问题, nvocation failed Server returned invalid Response. java.lang.RuntimeException: Invocation failed Server returned invalid Response. at git4idea.GitAppUtil.sendXmlRequest(GitAppUtil…...
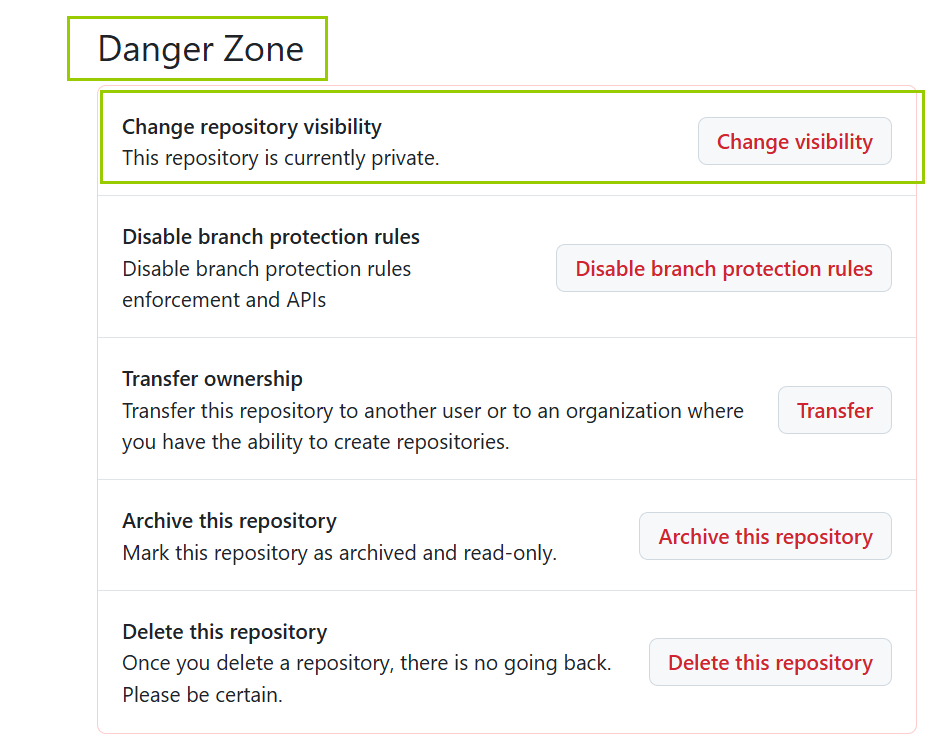
github | 仓库权限管理 | 开权限
省流版总结: github 给别人开权限:仓库 -> Setting -> Cllaborate -> Add people GitHub中 将公开仓库改为私有:仓库 -> Setting -> Danger Zone(危险区) ->Change repository visibility( 更改仓…...

MQTT客户端核心架构解析:clients.h源码深度解读
MQTT客户端核心架构解析:clients.h源码深度解读 一、头文件概览与设计哲学 clients.h作为MQTT客户端核心数据结构定义文件,体现了以下设计原则: 分层架构:网络层/协议层/业务层解耦状态管理:通过状态机实现复杂协议…...
